一种改进的三层SOM入侵检测方法

周方祥 万仁霞 解道锦 王玮琪

摘  要： 为有效侦查网络入侵行为，提出一种改进三层SOM神经网络入侵检测方法，旨在提高检测率和降低检测时间。该方法通过数据归一化、网络模型初始化、计算获胜神经元、权值调整等步骤训练模型，最后通过训练好的模型检测待测样本，以得到待测数据的分类结果。通过采用折中规则计算竞争层节点数优化初始模型，以及增加自适应停止训练机制克服原算法最大停止的缺点。实验结果表明，改进算法可在确保检测质量的前提下有效提高未知样本的检测效率。

关键词： 网络入侵; 自组织特征映射网络; 模型训练; 数据分类; 节点计算; 初始模型优化

中图分类号： TN915.08?34; TP391.9                文献标识码： A                   文章编号： 1004?373X（2019）15?0068?04

Network intrusion detection method with improved 3?SOM

ZHOU Fangxiang1， WAN Renxia2， XIE Daojin2， WANG Weiqi1

（1. School of Computer Science and Engineering， North Minzu University， Yinchuan 750021， China;

2. School of Mathematics and Information Science， North Minzu University， Yinchuan 750021， China）

Abstract：  In order to effectively detect network intrusion behavior， a neural network intrusion detection method with improved three?layer SOM is proposed in this paper to improve the detection rate and reduce the detection time. In the method， the model is trained according to the steps of data normalization， network model initialization， calculation of winning neurons， weight adjustment， etc. The samples under test are tested by the trained model to obtain the classification result of the data under test. The trade?off rules are adopted to calculate the number of competing layer nodes， so as to optimize the initial model， and add the adaptive stop training mechanism to overcome the maximum stop shortcoming of the original algorithm. The experimental results show that the improved algorithm can effectively improve the detection time efficiency of the unknown sample under the premise of ensuring the detection quality.

Keywords： network intrusion; SOM; model training; data classification; node calculation; initial model optimization

0  引  言

随着互联网的高速发展，网络入侵也频繁出现，网络侵害行为已严重阻碍生产发展[1]。但要实时且全面地找出网络系统中存在的真实入侵并不容易，因而检测技术的有效性就显得极其重要。

文献[2]提出一种改进的SOM网络入侵检测模型（3?SOM），在典型二层SOM神经网络基础上增加一层输出层，由无监督的神经网络变为有监督的神经网络。但该方法中的隐层节点数和训练次数依靠经验取得，一般认为，增加隐层数可以降低网络误差，提高精度，但也使网络复杂化，从而增加网络的训练时间和出现“过拟合”的倾向。另外，如果训练次数过多或过少，则会产生过拟合或欠拟合，这些情况都会影响检测入侵数据流的分类结果。

本文在文献[2]的基础上，提出一种改进的3?SOM（Improved 3?SOM，I3?SOM），引入竞争层节点数计算方法与自适应停止训练机制，有效地克服传统算法较长的训练时间，提高了模型训练的效率。

1  三层SOM神经网络模型

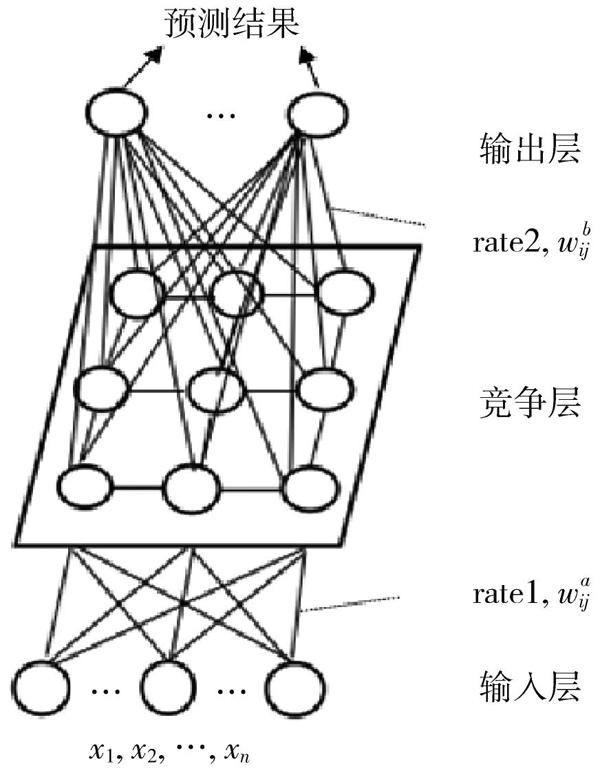
典型的自组织特征映射网络（简称SOM）模型有两层结构，即输入层和竞争层。SOM的基本思想是计算出各输入样本与互连竞争神经元的欧氏距离，最小的为获胜神经元。调整获胜神经元和与其相邻的神经元权值，使获胜神经元及周边权值靠近输入样本。经过反复多次训练，使得同类神经元具有相近的权系数。在学习过程中，学习率、权值和神经元邻域不断调整，异类神经元逐步发散，同类神经元相对逐步集中，从而达到聚类的效果。文献[2]在典型的两层SOM中增加了一层输出层，输出层的节点与测试数据的类别相同，使得无监督变成了有监督的全链接网络模型，如图1所示。相对两层SOM，3?SOM在输入层与竞争层的学习率rate1和权值基础上增加了竞争层与输出层之间的学习率rate2和权值。利用训练数据建立三层模型，检验待测样本的属性，通过计算待测样本与竞争层的最短距离以得出获胜神经元，与获胜神经元连接权值最大的输出层神经元为待测样本类别。

图1  三层SOM神经网络模型

3?SOM与BP神经网络有着相似的结构，BP模型包含输入层、隐层、输出层。两者都是通过调整权值以实现自适应学习，但两者权值的调整方式各异。3?SOM是正向使得同类的神经元具有相似的权系数，不同类的权系数差异较大，最终实现数据分类[3]。在BP网络中，样本数据从输入层经隐层逐渐向后传播，调整权值时，则沿着减少误差的方向，从输出层经过中间各层逐层修正网络的连接权值，以实现网络训练。

2  改进的三层SOM神经模型

针对3?SOM中存在竞争层节点数取值困难、训练次数不确定的问题，本文提出以下两点改进。

2.1  计算竞争层节点数

3?SOM输入层节点数一般为输入样本的维数，输出层节点数一般为输入样本的类别数，因此，网络模型的结构难点在于竞争层节点数的选择。竞争层节点数或多或少会导致过拟合或欠拟合，过拟合就是网络模型把非一般的特性也学习到;欠拟合就是难以学习到一般规律。所以竞争层的节点数影响着整个模型的结构，在很大程度上决定着三层SOM神经网络模型的学习速度和泛化能力。

在BP神经网络中，同样存在最佳隐层节点数难以确定的问题，一般有如下三种基于经验的近似计数法[4]：

式中：[m1]，[m2]，[m3]为三种不同公式计算得出的竞争层节点数;[n]为输入层节点数;[l]为输出层节点数;[α]为1～10之间的常数。

文献[5]运用“二分分割法”改进BP隐层节点数的问题，取[m1]，[m2]，[m3]中两个数的平均值，剔除最大均值，剩下两个较小的值作为节点数的取值范围，以此类推，逐渐缩小范围。文献[6]通过三种经验计数公式确定范围后，逐个代入训练方法中，以训练的误差绘制曲线图，取曲线图中最小值作为最优节点数。上述两种方法都是在实验中采用试凑法，这无疑增加了人工和模型的训练时间。

在3?SOM神经网络中的竞争层节点代表输入数据潜在的分类类别，其节点数一般大大多于数据实际类别[4]，本文引用上述计算BP网络模型隐层节点数的三个公式，并采用折中规则计算新的竞争层节点数：

这种方法根据节点数直接计算去掉了繁杂的人工试凑法过程，避免了过拟合或欠拟合两种极端情况的发生，通过多种网络入侵数据的实验，证明此方法的有效性。本文实验中[α]的取值为5。

2.2  自适应停止训练机制

目前的SOM网络模型一般要达到预先设定的最大迭代次数才会停止训练，所以，它的收敛速度相对比较慢[7]。从训练过程中发现权值的变化是由学习率、迭代次数决定的，从一开始给出的随机矩阵向量，经过网络模型的不断学习，逐渐改变权值，使之接近输出神经元的聚类中心，达到预先设置的最大迭代次数则停止训练。最大的迭代次数则靠经验设定，如果设置训练的次数过少或过多同样存在欠拟合或过拟合的情况，次数过多还会延长训练时间，对检测海量的网络入侵数据产生不良后果。本文采用权值误差机制自适应停止训练： [Δw]为误差因子，表示当前权值向量与前一次权值向量之差的绝对值，即[Δw=wn-wn-1]。当[Δw≤?] 时则停止训练，其中[?]表示误差因子下限，训练过程中误差因子[Δw]会不断减小。当[Δw]减小到0时，当前权值与前一次权值相等，所以[Δw]的值越小，越接近收敛。

2.3  I3?SOM入侵检测方法

在I3?SOM神经网络模型中，输入层和输出层的神经元节点数分别与输入数据的维度和类数相等，竞争层节点数采用折中规则计算，层与层之间通过权值全链接，在迭代训练的过程中权值不断调整，从而实现对数据提取和预处理，据此建立预测模型，根据预测模型对预测数据进行分类检测。步骤如下：

1） 归一化处理。为消除各维数据的量级差别，缩小量值的差异，减少处理时间，本文通过归一化处理将输入的样本数据都转化为[0，1]之间的数。归一化函数如下：[y=x-xminxmax-xmin]，[x，y]表示输入样本和归一化后的结果，[xmax，xmin]分别是输入样本中的最大值和最小值。

2） 初始化网络模型。即对网络模型初始化，设置输入层、竞争层、输出层的节点数、初始学习率、随机权值向量、初始节点邻域半径。设置初始学习率最值[8]rate1、rate2∈（0，1），邻域半径最值[rmax]，[rmin]，设置最大迭代训练次数[T]。根据折中规则计算竞争层的层数[m]。

3） 计算获胜神经元。利用欧氏距离[d=（xi-waij）2]选出获胜神经元，[xi，waij]表示输入样本、输入层与竞争层之间的初始权值，距离最短的即为获胜神经元。

4） 调整学习率、邻域半径和权值。

式（1）、式（2）表示输入层与竞争层、竞争层与输出层的学习率更新公式，其中，[k]表示从1开始的当前迭代次数;式（3）表示获胜神经元的邻域半径更新公式;式（4）、式（5）分别表示输入层与竞争层、竞争层与输出层的权值更新公式;[xi，yi]分别表示输入样本和样本类别。

5） 自适应停止机制，即判断误差因子[Δw]是否满足条件。实验中?取值为0.005，如果[Δw≤0.005]，則停止训练，否则转向步骤3）。

6） 输出分类预测结果。

3  实验结果与分析

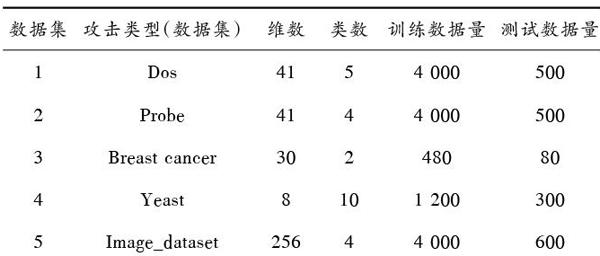
为检验I3?SOM在网络入侵检测中的有效性，实验参数设置如下：输入层与竞争层的rate1max=0.9，rate1min=0.01;竞争层与输出层的rate2max=0.5，rate2min=0.01;邻域半径最值[rmax=]1.5，[rmin=]0.3;最大迭代训练次数[T=]20 000。实验数据采用部分KDD99数据集和文献[9]中实验的数据集，如表1所示。根据大量的训练数据建立模型，对测试数据进行检测，以检验理论的可行性。

表1  实验数据集

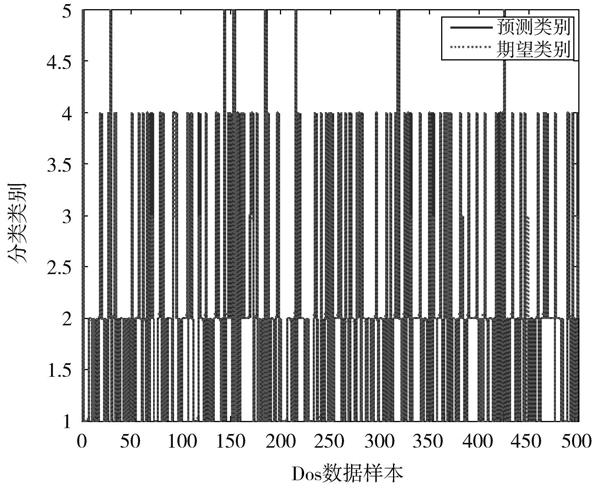
圖2  Dos检测分类效果

图3  Probe检测效果

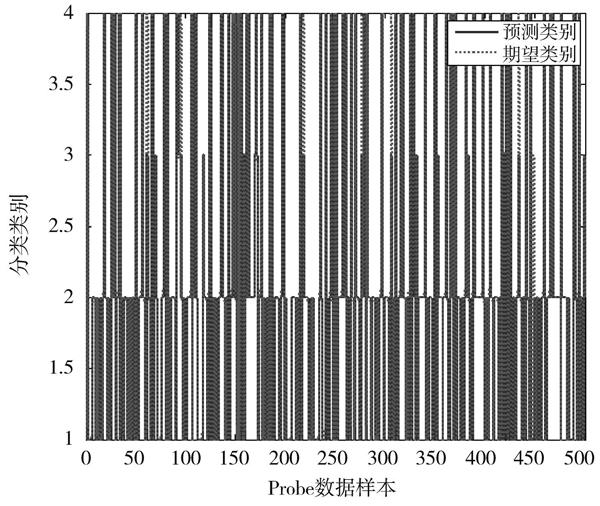
图4  Breast cancer检测效果

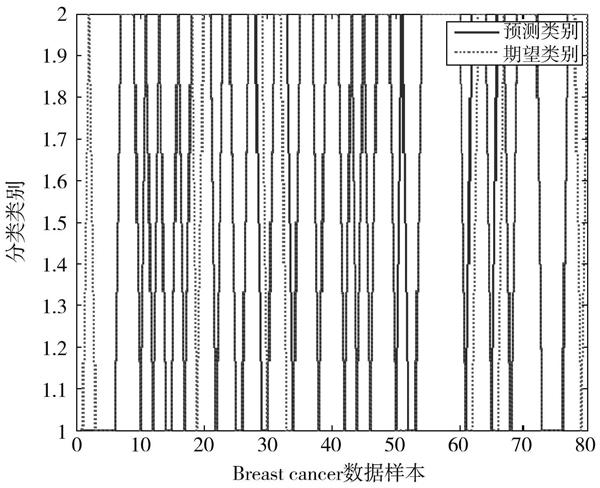
图5  Yeast检测效果

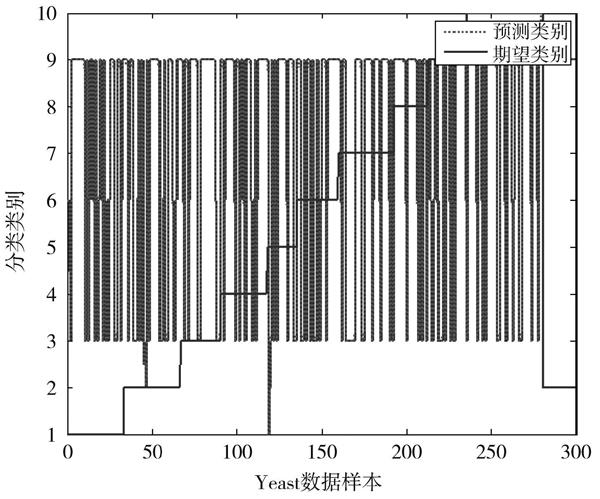
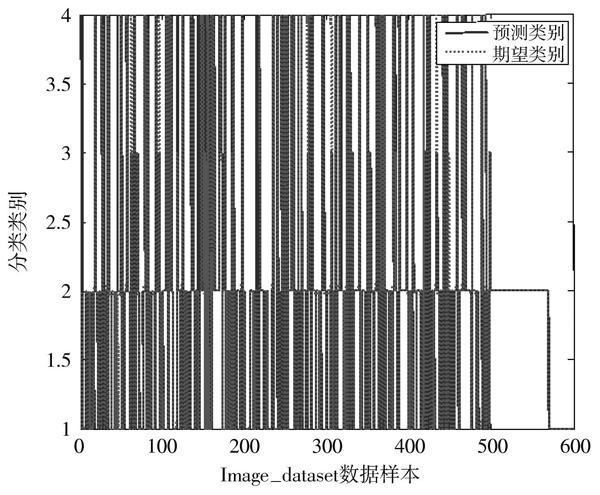
图6  Image_dataset检测效果

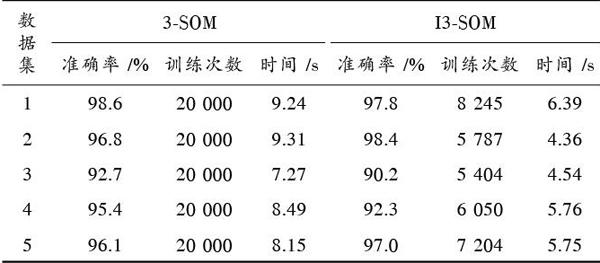
从表2中可以看出，I3?SOM的分类准确率均在90%以上，I3?SOM基本保持了3?SOM分类质量，在个别测试数据集上I3?SOM分类质量优于3?SOM。表明I3?SOM具有较高的分类质量。这是因为3?SOM算法训练和收敛的时间是迭代训练次数阈值设定决定的，为得到一个较理想的分类效果，迭代训练次数阈值的设置必须足够大（本文实验设置为20 000），而I3?SOM采用权值误差机制自适应停止训练机制和训练次数阈值以逻辑或条件的形式来控制算法收敛，从表2中可以看出，I3?SOM实际收敛迭代次数远小于预设训练次数阈值。同时，I3?SOM采用折中规则计算网络竞争层节点数，避免了复杂的人工试凑法，也降低了训练模型的时间。

表2  实验结果对比

4  结  语

I3?SOM实现了对入侵数据的有效检测，引入折中规则计算竞争层节点数以及自适应停止训练机制，降低了网络模型的训练时间，提高了检测效率。但误差因子下限的设置目前还是根据经验设定，过大会导致模型的泛化能力低下，加大检测结果的误差;过小又会增加迭代次数，导致时间开销增大。部分测试集预测效果的准确率不高，原因是自适应训练的次数较少，因此误差因子下限的寻优问题将是下一步的工作的重点。

参考文献

[1] SFAR ArbiaRiahi， NATALIZIO Enrico， Yacine CHALLAL， et al. A road?map for security challenges in Internet of Things [J]. Digital communications and networks， 2017， 3（4）： 1?2.

[2] 李昆仑，董宁，关立伟，等.一种改进Kohonen网络的Dos攻击检测算法[J].小型微型计算机系统，2017（3）：450?454.

LI Kunlun， DONG Ning， GUAN Liwei， et al. An improved Dos attack detection algorithm for Kohonen networks [J]. Journal of Chinese computer systems， 2017（3）： 450?454.

[3] 王小川，史峰，郁磊，等.Matlab神经网络43个案例分析[M].北京：北京航空航天大学出版社，2013：336?343.

WANG Xiaochuan， SHI Feng， YU Lei，et al. Analysis of 43 cases of Matlab neural network [M]. Beijing： Beijing Aerospace University Press， 2013： 336?343.

[4] 韩力群.人工神经网络教程[M].北京：北京邮电大学出版社，2006：73?74.

HAN Liqun. Artificial neural network tutorial [M]. Beijing： Beijing University of Posts and Telecommunications Press， 2006： 73?74.

[5] 阮翔.基于改进的BP神经网络库存预测模型及其应用研究[D].南昌：南昌航空大学，2016：17?25.

RUAN Xiang. Extremely applied research on inventory prediction model based on improved BP neural network [D]. Nanchang： Nanchang Hangkong University， 2016： 17?25.

[6] 陶刚，闫永刚，刘俊，等.基于改进的SOM聚类连续属性离散化算法[J].计算机应用，2015，35（z1）：89?92.

TAO Gang， YAN Yonggang， LIU Jun，et al.Distinct algorithm of continuous attributes based on improved SOM clustering [J]. Journal of computer applications， 2015， 35（s1）： 89?92.

[7] 张欢韵，李益才，蓝章礼.一种自适应停止的SOM神经网络及其应用[J].计算机时代，2014（4）：9?11.

ZHANG Huanyun， LI Yicai， LAN Zhangli. An adaptive stopping SOM neural network and its application [J]. Computer Era， 2014（4）： 9?11.

[8] 周志华.机器学习[M].北京：清华大学出版社，2016：97?99.

ZHOU Zhihua. Machine learning [M]. Beijing： Tsinghua University Press， 2016： 97?99.

[9] 王积丽.基于改进的模糊SOM算法确定最佳聚类数目方法的研究[D].广州：华南理工大学，2016：26?27.

WANG Jili. Research on the method of  deter?mining the optimal number of clusters base?don improved fuzzy SOM algorithm [D]. Guangzhou： South China University of Technology， 2016： 26?27.