基于三边测量的双重质心算法研究

杨思国，陶维青

1 引言

在研究煤矿井下人物定位系统时，首先要选择定位算法。不同的定位算法的定位精度、通信开销、硬件成本和能耗等指标是不同的，这就从前端决定了该系统的性能的高低。定位算法有两大类：基于测距(RSSI)的定位算法和基于非测距的定位算法。基于测距的定位算法需要测量出目标节点与多个参考节点的距离或角度，一般有三边测量法、三角测量法和极大似然估算法。不需要测量出目标节点与多个参考节点的距离或角度关系，而是依据无线网络节点的通信连接关系来估算目标节点的位置。2001年瑞士洛桑联邦工业大学的Srdjan Capkun等人最早提出的相对定位算法SPA是在没有测距的前提下的一种无线网络定位算法：通过无线网络节点建立一个全局坐标系统或局部坐标系统，通过坐标之间的相应关系对未知节点进行定位[1]。在此基础上美国仁斯利尔理工学院的Raj agopal Iyengar等人提出了一种基于聚类(Clustering-based)的定位算法；美国路特葛斯大学的Dragos Niculescu等人提出DV-Hop算法[2]。SPA、Clustering-based和DV-Hop算法都属于基于非测距的定位算法，虽然后两种算法针对SPA算法的缺点进行改进，但依然存在通信开销量大，定位精度差的现象。

基于测距的定位算法中的三边测量法，由于参考节点和目标节点自带测量芯片，因而不需要增加硬件成本。且通信量不大、能耗较低，定位精度明显高于基于非测距的定位算法。本文提出的基于三边测量的双重质心算法是在三边测量法和基于三边测量的质心算法基础上的一种改进算法。与三边测量法和基于三边测量的质心算法相比，定位精度进一步提高，是煤矿井下人物定位系统定位算法中一种不错的选择。

2 测距数学模型的构建

基于RSSI的定位算法的第一步是测量目标节点与参考节点间的距离或角度。角度测量需要目标节点和参考节点上装载天线阵列，成本较高，在这里不做讨论。距离测量在是依据电磁波信号在传播过程中产生损耗来估算距离的。其基本原理：己知发射信号强度，记录接收节点收到的信号强度，二者的差即是传播损耗，然后把损耗值代入相应的模型即可得到距离[3]。目前学者研究的电磁波信号路径损耗有4种模型，针对煤矿井下特殊环境，选取对数-常数分布模型，如下式：

(1)

在式(1)中d0表示基站到参考节点的距离，依据现场环境，在室内一般取lm，在室外一般取100m。Pd0表示在d0处接收到基站信号的强度(dB)，Pd是在距离基站d处目标节点接收到基站信号的强度(dB)。n表示传输路径长度与损耗的比例因子，一般为2～5之间的数值。εσ是标准偏差为σ的高斯随机变量，其平均值为零[4]。

由公式(1)即可计算出发射节点与接收节点之间的距离：

(2)

在实际测量中，电磁波信号传播受环境因素和环境变化的影响很大，导致理论模型计算值和实际传播损耗值有较大的误差[5]。如参考节点安装布置的高度和密度；电磁波信号在巷道、采矿工作区、挖掘工作区等不同区域传播的的反射、衍射、和多径传播效应；人或物的阻挡；天线增益变化等偶然因素和必然因素的影响。文献[6]提出采用卡尔曼-高斯混合滤波可以有效地减小最大误差、最小误差和平均误差。同时提出用最小二乘法分段曲线拟合算法对环境参数n和(Pd0+εσ)进行修正，这一点在现场调试中非常重要。采取这些措施可以将测距阶段的误差控制在一定的范围内，避免将过大的误差带入定位阶段，导致定位结果严重失真，定位失败。

3 三边测量法

利用上节数学模型，在通信半径内可测得目标节点和参考节点的距离。选择靠近目标节点U(X，Y)的三个参考节点A(X1，Y1)、B(X2，Y2)、C(X3，Y3)，已测得目标节点与三个参考节点之间距离分别是S1、S2、S3，以三个参考节点A、B、C为圆心，以对应距离S1、S2、S3为半径画圆，三个圆的交点即为目标节点，这就是三边测量法[7]。

三边测量法如图1所示。从图1可以得出

(3)

图1 三边测量法定位

由(3)式变换得出矩阵表达式：

(4)

由式 (4)可求出目标节点的坐标为：

(5)

应用最小二乘法可解得目标节点U的坐标估计值。

三边测量法的原理简单，基本思想很容易理解，但过于理想化。现实井下测距过程中因为障碍物、灰尘、硬件能耗以及用于测距相关的装置本身的仪器误差，致使目标节点到参考节点的间距测量存在的误差，三个圆难于交于一点，出现方程组无解的情况，也就使得三边定位失败[8]。因此需要其他的定位技术辅助处理，估算出相对合理的位置作为目标节点的坐标。

4 基于三边测量的双重质心算法

在三边测量法中会出现两种典型状况，一是测得目标节点到三个节点的距离比实际值小，如图(2)所示，方程式(5)无解。

图2 三边测量法定位

二是测得目标节点到三个节点的距离比实际值大，如图(3)所示，方程式(5)有解。

图3 基于三边测量的质心算法

在进行系统调试时，环境参数的选择一般应使测距正偏离，这样就出现图3状况。圆B和圆C相交于a和a’两点，其中靠近圆心A的a点是真解，a’点是干扰解。同样，圆C和圆A相交于b和b’两点，其中靠近圆心B的b点是真解，b’点是干扰解；圆A和圆B相交于c和c’两点，其中靠近圆心C的c点是真解，c’点是干扰解。假设a点坐标为(x1,y1),b点坐标为(x2,y2)，c点坐标为(x3,y3)。求a、b、c三点的质心即为目标节点U(X，Y)的估算值(定位坐标)U，(X，，Y，)。

(6)

上述方法就是基于三边测量的质心算法[9]。

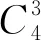
(7)

这种方法就是本文提出的基于三边测量的双重质心算法。

5 仿真与分析

在井下80m×80m测试区域内布置四个点参考节点，坐标分别标注为A(0，0)、B (0，80)、C(80，0)、D(80，80)。在测试区域内放置一个待测的目标节点，坐标为U(43，50)。则可以计算出U点到A、B、C、D点的实际距离分别为65.95m、52.43m、62.20m、47.63m。在参考节点和目标节点上安装TI公司生产的CC2530无线信号收发芯片，其自身带有定位功能。应用CC2530的定位功能进行测量AU(S1)、BU(S2)、CU(S3)、DU(S4)。为减少环境参数及随机噪声产生的误差，每个距离测量50次，并对数据进行卡尔曼滤波，最终得到四个距离量为72.55m、57.67m、68.42m、52.39m。

下面在Matlab仿真软件上进行仿真实验：

1.三边测量法

已知S1=72.55m,S2=57.67m,S3=68.42m 代入公式(5)数学模型，应用Matlab仿真，得到图4结果。

图4 三边测量法仿真结果

2.基于三边测量的质心算法

已知S1=72.55m,S2=57.67m,S3=68.42m 。按照基于三边测量的质心算法，应用Matlab仿真，得到图5结果。

图5 基于三边测量的质心算法仿真结果

3.基于三边测量法的双重质心算法

已知S1=72.55m,S2=57.67m,S3=68.42m,S4=52.39。按照基于三边测量的双重质心算法，应用Matlab仿真，得到图6结果。

图6 基于三边测量的双重质心算法仿真结果

表1

6 结论

从上述个例看，在同等条件下该算法的定位误差是三边测量法的11.2%，是基于三边测量的质心算法的6.3%有效地提高定位精度。经过大量反复的实验证明：采用基于三边测量的双重质心算法可以显著减少定位误差，且因本算法的对称性，可以抵消一部分在测距环节中由于环境因素相关的参数n造成的误差。

综上所述，可以得出如下结论：(1)由于每个节点模块自带测量定位功能，因而，改进后的基于三边测量的双重质心算法与前两种算法相比不需要增加硬件成本。(2) 基于三边测量的双重质心算法比前两种算法计算量略大，电池能耗增加，电池使用有效期变短。(3)改进后的基于三边测量的双重质心算法定位精度却明显高于三边测量法和基于三边测量的质心算法。