封开河预报模型研究进展
2019-08-08汪恩良
汪恩良,徐 雷
(东北农业大学 水利与土木工程学院,哈尔滨 150030)
我国北方高寒地区冬季,河流水面由于热力以及动力因素,逐渐形成固定冰层的现象称为河道封河;流动河道中冰盖消融破裂,自上而下流动的现象称为河道开河(或解冻)[1]。
冬季封河期,河流产生大量水内冰,受河段地理位置、水文气象条件、河道特性等因素影响,极易形成流冰堆积,导致过水断面狭窄,抬高水位,造成凌汛灾害;春季开河期,由于冰盖融化,流量增加,并且大量流冰块下移、堆积、拥堵河段,减弱断面过流能力,同样会造成凌汛灾害。封河及开河期都易产生水位上涨现象,引发凌汛灾害,因此凌汛的产生与封开河时间关系密切,故建立封开河预报模型至关重要。
封河及开河日期预报是运用历时收集和目前观测的水文、气象等数据,根据河流封开河规律,预报未来封河及开河日期。建立封开河日期预报模型,是冰凌情况预警的重要手段。根据预报结果,提前制定有效的防凌措施,降低凌汛灾害损失,对国民经济和社会可持续发展有着重要意义。
国内常见的封开河日期预报模型有3类,即数学模型、统计学模型和神经网络模型。本文对3类模型进行总结和分析,从影响因子选取和预报因子筛选方法两个方面入手,探究如何建立更为精准的封开河预报统计学模型和神经网络模型。
1 封开河日期预报模型介绍
国外对封河及开河预报的研究可追溯到19世纪八九十年代,其中Adams[2]利用经验公式成功地对圣劳伦斯河上游河段进行了封河预报;Greene运用自己改进的封河预报模型对圣玛丽河的封河日期进行了预报,得到了较为满意的结果;沈洪道[3-4]基于热交换原理进行了封河及开河日期预报,结果较为理想;Foltyn[5]采用数值模拟的方法成功建立圣劳伦斯河上游封冻时间预报模型。直到20世纪七八十年代, 我国的冰情系统观测研究才得到了全面的发展[6]。在1978、1982、1986[7]、1987[8]年,分别举办冰情研究和水文预报等会议,为冰情预报事业奠定了坚实基础。到21世纪,通过大量科研学者的不断钻研创新,新技术新方法的应用,冰情预报的研究进入了崭新的领域。目前,国内冰情预报的研究正处于一个不断更新和完善的阶段,各类数学模型、统计学模型和神经网络模型不断应用到封河及开河冰情预报中[9]。
1.1 数学模型
数学模型是以河冰生消物理机制为基础,根据水文学流量演算、热力学、冰水力学等物理方程,深入研究河段封河期及开河期的水、热特征。通过河段及其周边地区的气温预报信息、各水文站实测及预报水文信息,结合相关经验预报模型,对封河及开河日期进行预报[10]。
1.1.1 热力学模型
统一度-日模型是一种常用的封河及开河日期预报模型。主要考虑气温对河冰生消的影响。1980年Bilello[11]首次将米歇尔度日法公式进行改进;后来Shen[12]进一步改良统一度-日模型,成功预测圣劳伦斯河段河冰的热力生消和冰盖开河;吴金峰[13]将改良后的模型应用到万家寨库尾岔河口河段的开河预报中,在只考虑热力条件的情况下,成功预报开河日期。模型公式为:
1) 冰厚增长模型:
qi=ki(Tm—TS)/h
其中:qi为通过冰盖的热通量;ki为冰的热传导;Tm为冰水界面的温度;TS为冰盖顶面的厚度,h为t时刻的冰厚。
2) 冰厚衰减模型:
h=(h0+αS)1/2—βTθ
其中:T为自冰盖形成以来的天数;β和θ为随地点而改变的经验常数;α为经验常数。
气温是影响河冰生消变化的关键因素,是封河及开河预报的重要因子。统一度-日法充分考虑气温对封河及开河日期影响,提高了预报的效率和准确度。只考虑气温,并不能完全反映封河及开河期冰凌变化的物理过程。故部分学者在此基础上,将水力学模型与热力学模型相结合预报封河及开河日期。
1.1.2 热力学模型与水动力学模型耦合
陈赞廷[14]等根据热量平衡原理及水力学理论,预报封河及开河日期,优化三门峡水库防凌调度。采用一维对流、扩算方程作为水温计算模型:
式中:ρ为水的密度;Cρ为水的比热;A为断面面积;TW为水温;Q为流量;Ex为扩散系数;B为河宽;H为每单位面积热交换率;t为时间;X为距离。
1) 封河预报模型:
Fr+Uef+Uif=f(Ci,T∂-)
Ft=f(Q)
CiT∂->aQ则封河
式中:Fr是摩擦阻力;Uef是黏附力;Uif是冻结力;Ft为流冰推动力;Q为流量;T∂-为负气温;a=0.008。
2) 开河预报模型:

∑Qu≥1.2Qm武开河
∑Qu<1.2Qm文开河
式中:∑Qu为上游总来水量;hm为封冻期间最大冰厚;∑Ta+为气温稳定转正累积正日平均气温;Qm为冰盖下过流能力。
模型将水动力学模型与热力学模型相结合,使预报模型更加贴近实际,提高预报精度。并且将开河方式进行划分,更能反映真实野外河冰生消变化过程。
1.1.3 结合水文学流量演算的封河日期预报模型
可素娟[15]等在水力学模型和热力学模型相结合基础上,首次考虑了河道形态的影响,在黄河内蒙古河段建立封河日期预报模型,此模型准确性高,通用性强。
封河预报模型为:
式中:Fs为冰凌阻力;Ft为曳引力;Q为流量;T∂-为负气温;R=BS/J为河道条件,B为上下断面河宽比,S为河道弯曲度,J为水面比降;Ci为流凌量,采用一维对流热量扩散方程来计算:
式中:ρi为冰的密度;Li为结冰潜热;ΦT为水与空气的热交换率;A为断面面积;Ex为扩散系数;t为时间;X为距离。Q可用水文学模型中的马斯京根流量演算模型进行计算,马斯京根方程是河道流量演算中被广泛应用的方法, 它用槽蓄方程代替复杂的水动力学方程, 极大地简化了计算。马斯京根流量演算方程为:
Qi=C0Ii+C1Ii-1+C2Qi-1
式中:Ii、Ii-1为时段始末入流量;Qi、Qi-1为时段始末出流量;K、x分别为河段流量传播时间和流量比重因子;Δt为入流出流的时段长度。
模型将水动力学模型与热力学模型耦合,并结合水文学模型,极大简化计算过程。首次考虑河道形态对封河日期的影响,更加接近封河期冰凌变化的物理过程,提高预报精度,并且可以在不同区域使用,具有通用性。在流凌密度计算方面,采用从初始流凌一直计算到封河期的方法代替原有的递推法,避免由于传播时间不准造成的误差,使得计算更加方便实用。但模型对断面资料精度要求高,连续完整的河道地形数据难以获得,致使模型预报日期离实际情况仍有一定差距。
1.2 统计学模型
统计学模型是通过了解影响封河及开河因素,主要包括动力因素、热力因素、河势因素和人为因素,筛选预报因子,通过统计分析技术,与预报要素建立联系进行预报。
1.2.1 多元线性回归模型
回归分析原理简便,清晰易懂,是目前统计分析中比较常用的方法。它不仅提供了一种建立变量间关系的数学表达式的方法,而且对所建立的经验公式的有效性进行分析、讨论和判明,同时判断如何利用所得到的经验公式来达到预报、控制等目的[16]。田京楠[17]、乔继平[18]、张一兵[19]等分别运用多元线性回归方程法对汤旺河五营站、三湖河口站、黄河宁蒙河段进行封河及开河日期预报,预报合格率均符合规范要求。
多元线性回归分析就是描述两个或两个以上自变量与因变量之间的线性依存关系,根据自变量的最优组合,建立多元回归方程,来预报因变量的变化。
多元线性回归模型可表示为:
yi=b0+b1xi1+b2xi2+…+bKxiK+ε
其中:y为研究对象即本文中的实测封河或开河日期,也被称为因变量或解释变量;xij(j=1,2,…,K)为K个影响因素即本文中的预报因子,也叫做自变量或解释变量;ε为各种随机误差对y所产生影响的总和,ε~N(0,σ2);bi(i=0,1,2,…,K)为回归系数。
多元线性回归模型具有操作方便、原理简单等优点。但将预报因子与预报对象之间的非线性关系简化为线性关系,这与实际情况并不完全相符。当影响因素较多较复杂时,多元线性回归模型预报准确性大幅降低。
1.2.2 投影寻踪回归模型
投影寻踪的基本思想:把高维数据投影到低维(1—3)可视空间上,寻找能反映原高维数据结构或特征的投影(称为“令人感兴趣”的投影),然后通过分析研究投影数据以达到了解原数据的目的[20]。投影寻踪回归模型就是基于投影寻踪思想建立,是一种解决高维空间回归问题的模型。王志兴[21]尝试将基于Hermite多项式的参数投影寻踪回归模型引入到冰情预报中,对黑龙江上游河段冰情长期预报,预报合格率高达100%。其数学表达式为:

在参数投影寻踪回归中,为了避免使用庞大的函数表,并且还要保证精度要求,一般采用可变阶的正交Hermite多项式拟合其中的一维岭数。数学表达式为[22]:

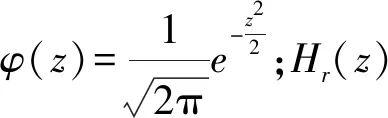
可变阶的正交 Hermite 多项式拟合一维岭函数,计算简单,能够保证模型逼近的精度, 能充分利用数据中的信息,无论对正态或非正态,线性或非线性数据都能有效地处理,稳定性好,精度较高。对于非线性的封河及开河日期预测也比较合适。但是投影寻踪回归模型在处理多个不同特性参数的优化问题时,存在收敛速度慢、参数不易调整等问题,并且无自学习自组织能力,大规模并行处理能力也有不足。这些缺点易导致模型精度降低。
该模型目前只应用在黑龙江河段,对于其它河流的适用性,需要经过进一步实践,才能综合分析其优缺点。
1.3 神经网络模型
人工神经网络是由大量神经元节点互连而成的复杂网络,是反映人脑结构及功能的一种抽象数学模型[23]。它以大脑的生理研究成果为基础,其目的在于模拟大脑的某些机理与机制,实现某个方面的功能[24]。它利用大批量的样本进行多次重复的学习,把样本内在关联归纳总结出来。目前,应用最为广泛的神经网络模型有两种:BP模型和GA-BP模型。
1.3.1 BP人工神经网络模型
BP人工神经网络全名为误差反向传播算法,它是一种多层前向型神经网络,其权值的调整采用反向传播学习算法[25]。张璐[26]利用BP人工神经网络模型、陈守煜[27]将模糊理论与BP人工神经网络相结合、卢海[28]采用单隐含层BP网络,分别对万家寨上游河段、黄河宁蒙段和松花江哈尔滨河段进行封河及开河日期预报,结果均符合精度要求。
BP人工神经网络模型是模拟人脑功能建立的。它作为智能方法的一种,具有信息的自学能力、环境的自适应性、网络之间的非线性映射能力、信息处理的容错性[29],相对于多元线性回归方程,它更适合于处理非线性问题,封河及开河日期预报准确性更高。但经过不断实践发现,BP神经网络算法本身存在一些缺陷:①没有确定隐含层神经元的最佳数量;②它的初始权值和阈值都是随机生成,缺乏必要的依据。这就很容易导致网络陷入局部极值点,导致预报精度下降。
1.3.2 GA-BP人工神经网络模型
GA-BP人工神经网络模型是把遗传算法与人工神经网络相结合,优化神经网络性能,使BP网络系统变得更加高效。苑希民[30]运用GA-BP模型、王志兴[31]应用改进的GA-BP交叉训练算法,对松花江依兰、佳木斯江段,进行封河及开河日期预报,取得良好结果。
GA-BP模型在BP人工神经网络基础上,结合遗传算法的优点,完善BP算法在初始权值和阈值选取上的不足,使其拟合数据的效果更加精确。
模型具有一定的预报能力,但不能客观地反映封河及开河时期冰凌的变化特点,特别是冰凌变化的物理过程,致使预报精度降低。
2 影响因子选取及预报因子筛选方法
经过不断的实践发现,建立预报模型目前存在两个问题:①通过封河及开河的物理成因进行影响因子的选取,具有一定的主观性和随机性;②在筛选预报因子过程中,应用不同的筛选方法,会导致最终建立的预报模型有所不同。本文从影响因子选取和预报因子筛选方法两个方面入手,探究如何建立更为精准的封开河预报模型。
2.1 影响因子的选取
研究学者大多是在分析影响封河及开河成因因素的基础上,筛选预报因子,建立预报模型。冀鸿兰[32]、胡进宝[33]、冯国娜[34]、史新娟[35]等在建立预报模型时,将影响成因因素概括为4类即动力因素、热力因素、河势因素和人为因素。即使针对同一河段的预报,由于出发点和方法不同,影响因子选择也会不同。丁雪慧[36]对漠河和哈尔滨地区河流建立封开河日期预报模型,选取累积负积温、风速、日照时长、水位 、流量等作为影响因子;王富强[37]应用流量、累积负气温、水位等作为影响因子,建立预报模型;王涛[38]选取累积负积温、负气温持续天数、流量、水位等作为影响因子对石嘴山河流进行封河日期预报。表1对应用较多的影响因子进行归纳总结。

表1 应用较多的影响因子
注:表1中影响因子按近十几年文章中应用次数排序。
累积负气温和负气温持续天数两个影响因子表征封冻期寒冷程度;开河前累积正气温和正气温持续天数表征开河前的温暖程度;封冻期降雪总量是反映冰上覆雪厚度大小的一个热力影响因素。冰上覆雪越厚,单位时间内,冰盖与大气之间的热量交换就越小,雪对冰与大气之间的热传递起到了阻碍作用,所以温度升高,有厚厚的积雪区域不易融化,从而延缓开河时间;水流速度主要对河冰搬运产生影响,当水流速度较小时,水流的动力作用就小,水位变化小,流凌很容易在河水中形成稳定的冰盖,致使封河时间变短;水位主要影响开河形式,水位平稳能使大部分冻冰就地消融形成“文开河”形势,水位急骤上涨能使水鼓冰裂形成“武开河”形势;流量的大小直接影响着水流速度和水位的大小,当过水面积不变,流量增大,水流速度随之变大,水位也会上涨,间接影响着封河及开河时间。流量的增加,还会使水体储存的热量增加,结冰时间就会变晚[28];顺着水流方向的风速越大,水流速度越大,水中漂浮的流凌速度也就越大,所以风速也影响着封河及开河时间。
2.2 预报因子筛选方法
选择适当的预报因子,对封开河预报模型的建立尤为重要。一般预报因子筛选采用相关系数法,逐步回归分析法和灰色关联分析法。王志兴[21]采用逐步分析法筛选预报因子对黑龙江上游江段开河日期进行预报,合格率达到了100%;冀鸿兰[39]、李海英[40]、薛小辉[41]等利用相关系数法筛选预报因子,对黄河内蒙古段和宁蒙段进行开河日期预报,所得结果均符合精度要求;李成振[42]基于灰色关联度分析法筛选预报因子,建立漠河站开河日期预报模型,预报合格率为50%。
2.2.1 逐步回归分析法
逐步回归分析法的基本思想是,当被选入的变量在新的变量引入后变得不重要时,可以将其剔除;被剔除的变量,当在新变量引入后,变得重要时,又可以重新选入方程[43],即逐个将新变量引入方程,设定显著性水平,利用显著性检验判别该变量是否符合被选入的标准;当有新的变量引入方程时,使得被选入的变量变得不再显著时,则将其剔除,如此反复进行,直到方程不再选入也不再剔除变量为止,这样就确保所选因子是最优的。
2.2.2 相关系数法
相关系数法反映了变量间相关关系的密切程度,按积差方法计算,以两变量与各自平均值的离差为基础,两个离差相乘来反映两变量间的相关程度[44],即将待选因子分别与实测封河及开河日期进行相关性分析,得到相关性系数,通过控制阈值大小,来选取预报因子。
2.2.3 灰色关联分析法
灰色关联分析法,从几何角度分析,是将比较数列与参考数列的曲线形状进行对比,得到两者之间的关联度。灰色关联分析法的核心是计算关联度。一般来说,关联度的计算首先要对原始数据进行处理,然后计算关联系数,由此就可以计算出关联度[45]。关联度越大说明两者之间关系越密切。与相关系数法相比,灰色关联分析法计算时不需要太多数据,对数据要求不高,计算过程不是很繁琐,涉及变量不多,很容易操作。
相关系数分析法,是通过计算相关系数,筛选出相关系数大的变量;灰色关联分析法通过进行系统发展势态的量化比较与分析来确定预报因子的优劣[42]。无论是利用相关系数法还是灰色关联分析法进行因子筛选,两种方法都是将单一的影响因子和封河或开河日期进行单独考察,分析之间的联系程度,忽略了影响因子相互之间产生的影响。逐步分析法依据它的计算过程,不仅考虑单一影响因子对封河或开河日期的影响,通过反复检验,兼顾考虑影响因子相互之间产生的影响,修正影响因子之间的多重共线性,使最终求得的预报模型更加精准。经过对预报模型的总结分析,本文认为预报因子个数控制在3~6个比较好,选择过少,预报模型没有代表性,选择过多则降低模型的稳定性。
3 结 语
通过对比分析3种封开河预报数学模型、两种封开河预报统计学模型和两种神经网络模型,得出以下结论:热力学与水力学相结合,考虑河道形态因素的影响,更能符合实际封河及开河时期冰凌变化的物理过程,提高预报精度;多元线性回归模型将非线性关系近似处理为线性关系,当影响因素较多较复杂时,预报准确性大幅降低;投影寻踪回归模型无论对正态或非正态、线性或非线性数据都能有效地处理,稳定性好,精度较高。对于非线性的封河及开河日期预测比较合适;GA-BP模型弥补了BP模型的初始权值和阈值选取问题,精度更高;筛选影响预报精度的13个预报因子,且对比分析3种筛选方法,发现逐步回归分析法不仅考虑单一影响因子对封河或开河日期的影响,且修正了影响因子之间的多重共线性,理论上来说,它优于其他两种方法。
