隧道下穿工程施工经验公式参数探讨

■ 中铁十八局集团第五工程有限公司 杨增朝

1.引言

随着城市建设的发展，轨道交通建设呈现出欣欣向荣之势，越来越多的穿越工程出现在城市的地下工程建设之中。在地铁隧道的下穿施工过程中，既有隧道的安全问题一直是工程的重点关注对象，保证施工进度的同时确保既有隧道的安全具有重要的意义。多名学者以往对地铁隧道下穿施工进行了大量的研究，其中经验公式法因其有效、实用的特点而被广泛应用。经验公式可以对隧道开挖引起的地层位移进行预测，且在以往的研究中应用效果良好，但是利用经验公式以实测值为基础进行反分析的研究相对较少。本文在实测数据的基础上，利用经验公式进行反分析计算，结论可为相关工程提供借鉴[1]-[2]。

2.工程背景

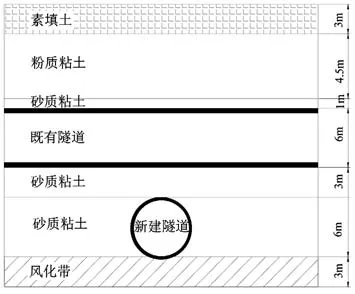
图1 地铁9号线地层剖面图

深圳地铁9号线管片外径6.0m，埋深9.1m～18m，上覆土层如图1所示，以粉质黏土、砂质黏土为主，隧道所在地层主要是砂质黏土。在建设过程中，某区间穿越地铁4号线，4号线盾构隧道外径同样为6.0m，拱顶覆土厚度为8.5m左右。9号线新建隧道以81°左右的角度穿越既有4号线，在穿越过程中左右线分别穿越两次，共计4次穿越。新建隧道与4号线既有隧道之间的净距在3.0m左右，具体距离如图2所示。

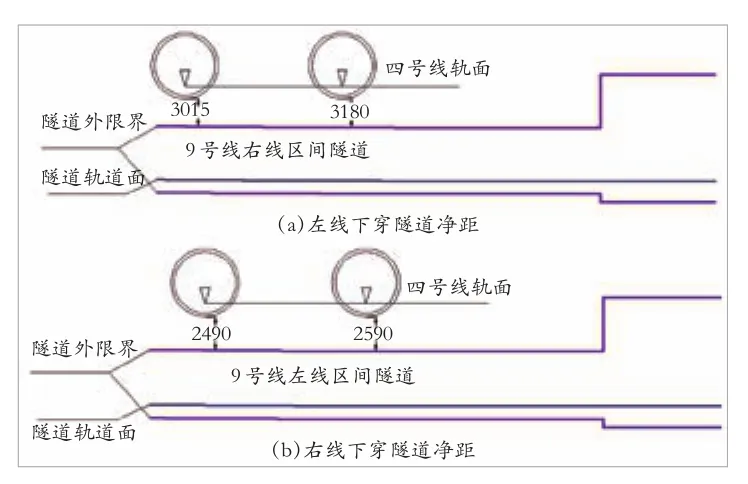
图2 下穿施工隧道间净距

3. Peck公式沉降计算

3.1 基本假定

Peck公式是以沉降槽的面积与地层损失之间的等量关系为基础，进行适当的地层假设而得到的经验公式。本文在运用Peck公式的前提下，在计算时进行了如下简化：

（1）选取既有盾构隧道轴线所在位置的剖面进行分析；

（2）假定新建隧道与既有盾构隧道垂直（实际角度是81°）；

（3）计算时将既有线隧道假定为弹性模量很大的土层。

3.2 数据拟合计算

Peck公式[3]已在地铁隧道工程中应用多年。在过去的研究中，部分学者[4]-[5]发现，Peck公式在地表以下的地层中同样适用，甚至可以很好地预测既有隧道或者既有管线的竖向变形。

根据Attewell等[6]提出的公式对其进行计算，在隧道穿越施工过程中计算既有线的变形时，可以假定既有隧道的底边为新建隧道开挖的地表，从而根据Peck公式，取上下两个隧道间的净距。计算公式如下所示：

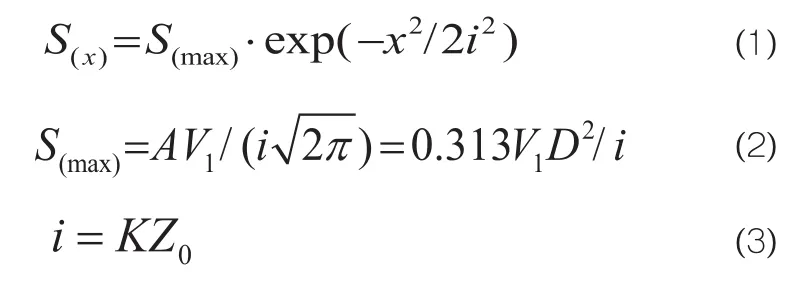
工程中共有四次下穿，如图2所示。本文针对四次下穿施工所测的数据，利用公式(1)对数据进行拟合计算，之后再利用公式(1)～(3)的等量关系，对其中的参数进行反分析。文中所取的实测值为盾构机推过既有隧道后5小时时间点的数据，此时盾构机推过了一段时间，既有盾构隧道已经有充分的时间发生变形，这些变形基本上是由于地层损失所引起的，这正符合Peck公式的原理。Peck公式只考虑了地层损失所引起的上覆地层变形沉降，而忽略了地层固结所带来的沉降。选取这个时间点的数据作为实测值来进行参数的反分析计算更为合理。

实测数据采用origin软件进行处理，得到拟合曲线。在拟合时选取两隧道的交点处为0，x轴方向为既有隧道纵向方向。实测数据值和其相应的拟合曲线如图3所示。从图3可以看出，断面1和断面3的拟合曲线相对较窄，断面2和断面4的曲线相对较宽，断面3和断面4的沉降值较大，而断面1的沉降值最小。无论拟合曲线如何，各个断面的实测值拟合程度均较好。

拟合曲线的具体参数如表1所示。从表1中可以看出，断面3和断面4的最大沉降值均在断面1的最大沉降值的2倍以上，断面2和断面4的反弯点到曲线中心的距离是断面1的距离的2倍。从表1中还可以得到，拟合曲线所在的中心线并非在x=0处，而是存在一定的偏差，断面1、断面2和断面3均在x轴的左侧，断面4在x轴的右侧，且就偏离距离而言，断面3和断面4偏离x轴的距离较远。

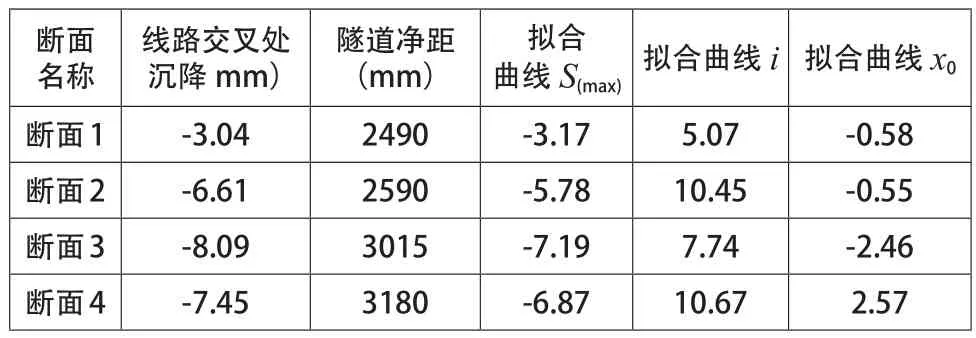
表1 不同断面拟合曲线参数

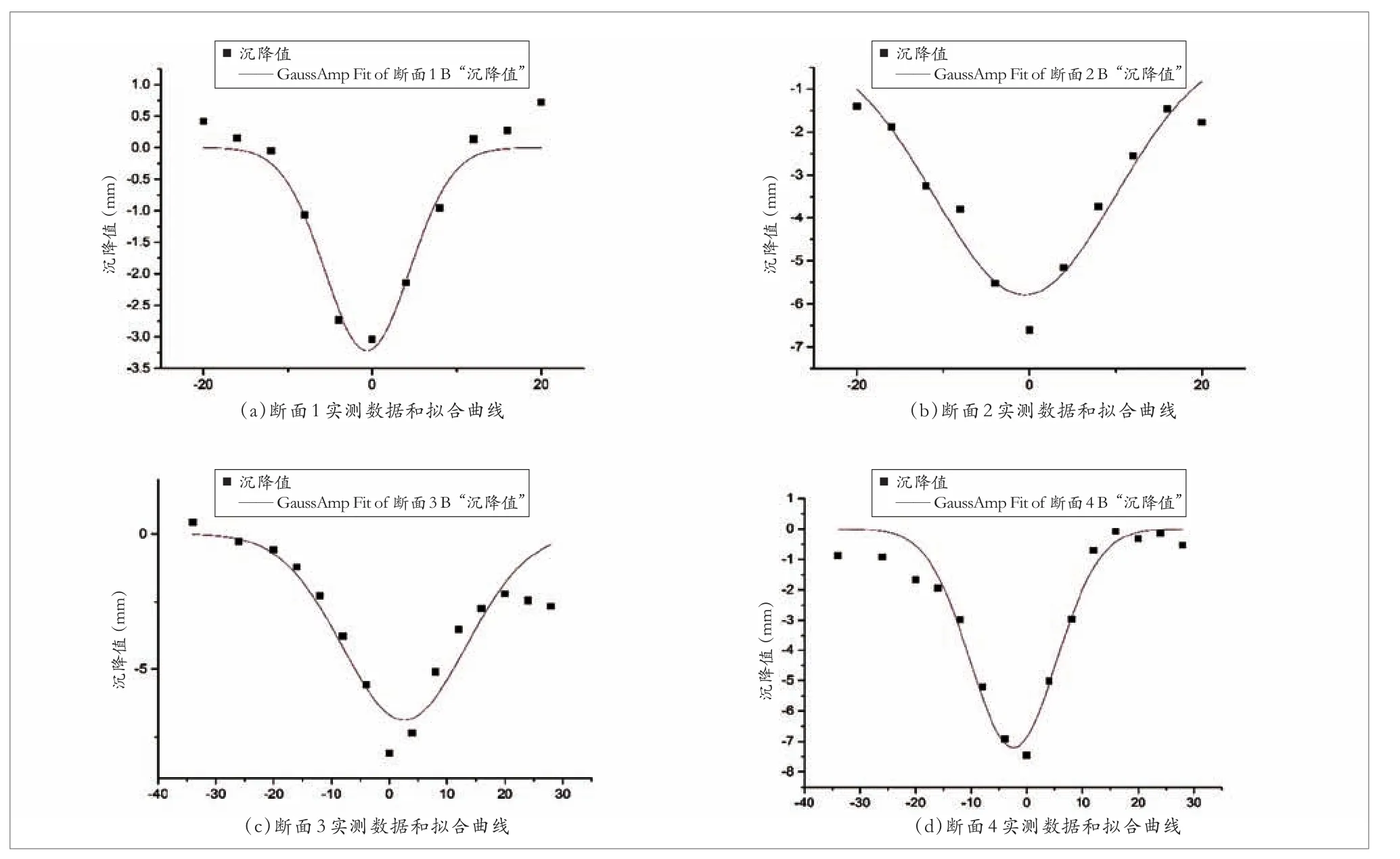
图3 既有隧道沉降值拟合曲线

4.参数讨论

根据Peck公式可知，比较重要的参数有最大沉降值S(max)、反弯点到曲线中心的距离i、沉降槽宽度系数K。通过具体的工程实测数据拟合曲线来反分析，最大沉降值是已知的，此处只讨论另外两个参数。

4.1 沉降槽宽度系数讨论

根据上述公式（3）可知，宽度系数K可以通过i与Z0得到。具体的沉降槽宽度系数如表2所示，之后对4个不同断面的宽度系数值进行平均，得到最终的沉降槽宽度系数平均值。

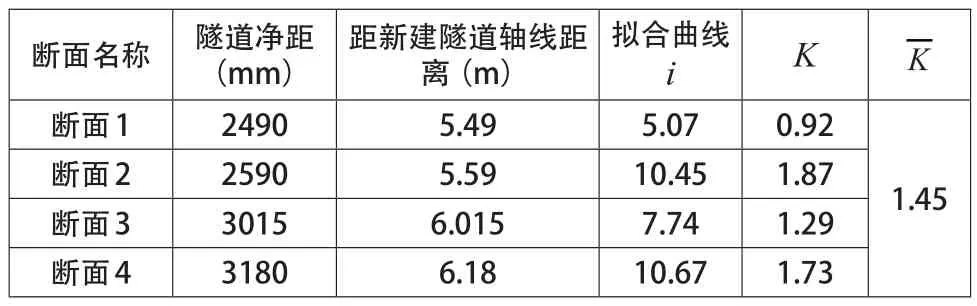
表2 沉降槽宽度系数求解

从表2中得到的数据可知，最终的沉降槽宽度系数平均值为1.45，大于单一隧道引起地表沉降所得的沉降槽宽度系数。因为天热地层的沉降槽宽度系数一般不超过1，大多在0.3-0.6之间[7]。沉降槽宽度系数增大的原因在于既有隧道刚度较大，在新建隧道开挖后对上覆地层的沉降具有阻挡作用，从而造成沉降槽宽度相对较大。

4.2 地层损失系数讨论

根据公式（1）～（3）可以推导出地层损失率V1与最大沉降值之间的关系式（4）。根据公式（4）结合实测数据所得出的拟合曲线参数，即可得到各个不同断面的地层损失率，如表3所示。

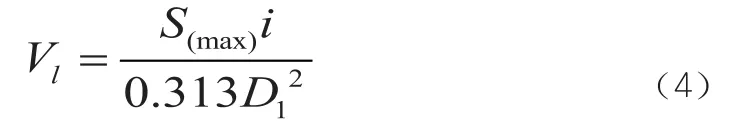
从表3中可以看出，断面1的地层损失率最小，断面2、断面3、断面4的地层损失率均在0.5%左右，就整体而言，各断面的地层损失率较小。

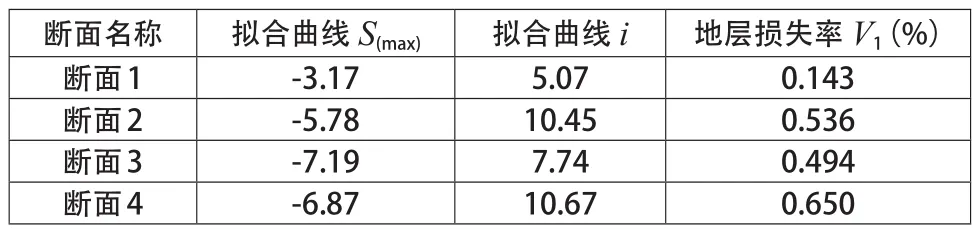
表3 地层损失率求解

假设新建盾构隧道在开挖过程中的地层损失只是由盾构机与管片之间的空隙所引起的，排除超挖的情况。盾构机与管片之间的空隙在施工过程中会有浆液填充，从理论上而言，注浆的区域为一圆环，且与管片环的圆心相同。如此即可通过几何关系得出在不考虑超挖情况下的地层损失率，如公式（5）所示。

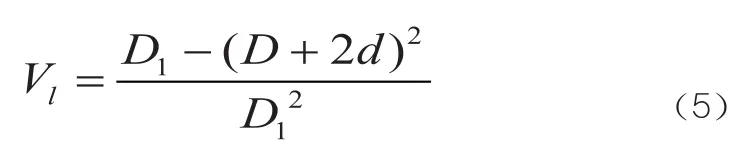
式中：D1为盾构机刀盘的直径，取6.28m；D为管片环的外直径，取6.0m；d为注浆层的厚度。

结合公式（4）和公式（5）即可求得注浆层的厚度，此时的注浆层厚度为实测数据反分析得到的厚度值。该工程反分析得到的注浆层厚度为13cm，而由盾构机刀盘直径6.28m可知理论上的注浆层厚度为14cm。虽然实际注浆层的厚度略小于理论值，但是相差很小，注浆层厚度达到理论值的93%，注浆效果良好，达到了注浆要求。

5.结论

基于新建隧道下穿既有盾构隧道的实测数据，利用Peck公式对数据进行拟合，并对拟合后的相关参数进行反分析，最终得到如下结论：

（1）利用Peck公式来反分析既有隧道的变形相关参数是可行的。Peck公式的拟合效果较好，得到的反分析参数也能很好地反映工程实际情况，值得推广。

（2）反分析得到的沉降槽宽度系数比纯天然土层的系数要大，说明既有隧道确有阻挡地层位移向上发展的趋势。

（3）反分析可得到地层损失率，进而可推导出注浆厚度。该工程中注浆厚度达到理论值的93%，表明注浆效果良好。

（4）现场应注意加强数据的监测与收集，充足的实测数据可以准确地反映已完成工程的实施效果，为下一步的工程开展提供借鉴。