轨道交通应急资源储备点选址优化研究

何 舟，徐永能，王笑天

(南京理工大学， 南京 210094)

近几年来，我国城市轨道交通建设投资规模庞大，诸多城市都开始建设轨道交通或是扩大现有轨道交通规模。在这样的背景下，如何应对应急突发事件显得尤为重要，也对应急管理提出了更高的要求。现实情况中，应急资源通常是指在发生应急突发事件之后，将现有的应急救援资源点的物资通过一定的方式与途径派送到事故点，从而起到参与救援的作用。因此，在应急救援中，应急救援点的设置问题以及应急物资的配置问题关系到整个应急救援体系的效率。而当出现重大事故或大型突发事件时，往往需要多个应急站点同时配合参与才能保障救援的快速有效。所以，科学有效的设置轨道交通应急资源储备点对于快速有效应对突发事件起着至关重要的作用。

在实际运营中，关键节点对于城市轨道交通的重要性不言而喻。为有效保护关键节点，本文设置了应急需求点关键度权重，综合考虑距离、救援效益等因素，在关键度权重下建立多目标规划模型，从而使得关键节点获得尽可能多的应急资源覆盖保障。期望能通过对关键节点的保护，能有效应对轨道交通突发事件，保障线路运行安全。

本文行文结构如下：第一章对众多学者已开展的应急资源储备点设置研究问题进行综述分析；第二章对本文涉及的储备点设置问题的前提条件进行假定；第三章建立了关键度权重下的多目标规划模型，并进行了条件约束；第四章使用算例，对建立的模型进行实际算例计算，验证模型的合理性；第五章则对文章进行最终的总结。

1 文献综述

对于不同环境下的应急资源配置研究问题已开展诸多研究。肖传宇[1]以高速公路网络化运行为背景，提出了基于网络化条件下高速公路沿线应急资源配置点选址模型，并给出了模型的算法流程以及求解步骤；方晨[2]则重点研究了海上突发事件的应急资源配置方法，运用柯布一道格拉斯生产函数建立确定最优分配方案的应急资源优化配置模型。

对于轨道交通应急资源的储备点以及资源调配优化问题，众多学者也做出了自己的研究。在不确定性条件下，刘畅[3]以典型的突发事件——地震为背景，运用基于随机需求的两阶段机会约束规划模型对应急储备库的选址于资源配置规划问题进行研究；汤兆平等[4]建立多目标规划模型，运用基于TOPSIS方法和限定参数区间搜索的模型求解方法对不确定需求的铁路应急资源调度问题展开了研究。

在模型建立上，部分学者使用了多目标模型进行建模求解。牟海波等[5]建立了在铁路应急物资储备点的运输能力约束和应急物资需求点的需求约束条件下的双目标规划模型对铁路应急物资的储备点选址问题进行了研究；孙剑萍、宫素萍等[6]建立了基于集合覆盖模型的，以应急资源配送时间最短和应急成本最低为目标的多目标规划模型，并进行了应急资源储备点实证分析；王普等[7]建立了以铁路应急救援开始时间最早、铁路应急资源输送可靠性最大、应急救援出救点数目最少的多目标优化，并运用分层序列法进行求解。

李卫军等[8]则是通过探讨网络化条件下轨道交通应急抢险要求，资源配置影响因素、配置流程等方面，分析不同覆盖模型下的应急资源选址问题，并使用实例进行了分析论证。冉连月等[9]通过考虑空间、成本、救援三个约束，建立了“P-中心”下的应急救援站选址模型，并通过线网脆弱性对比分析证明模型选址的可靠性。龙京等[10]则从不同角度出发，通过构建急管理能力评价指标体系,并进行实例论证，提升铁路应急管理能力。

从诸多学者的已经进行的研究来看，学者对于应急储备点的选址考虑因素大多在于空间、成本、救援时间等方面，并进行资源配置流程的梳理，由此采用的模型方法使用较多的为多目标规划法，以此实现对于两个以上预期目标的综合考虑，由此可见对于多目标问题的研究具有一定的借鉴意义。同时发现，对于轨道交通线路中存在的重要关键节点的保护并不十分突出，因此，参考多目标规划方法，综合考虑应急时间、应急救援站数量，最有效覆盖等多方面因素，同时考虑关键节点的重要度情况，建立了关键度权重下的多目标应急资源储备点选址模型，并进行计算分析。

2 问题描述

应急资源储备点的选址问题是个多目标综合考虑的问题，其中最为突出的目标就是时间最小化以及效益的最大化两个目标。如何在时间最小化的基础上满足最大的应急救援效益是其中的关键问题。基于此，引入应急需求点关键度权重，在此权重下优先保证关键节点的应急需求，在最短时间内取得最大的救援效果，从而构建高效可靠的轨道交通应急救援系统。为了更好的对问题进行分析，现对以下条件进行设立：各应急救援点之间的物资可以进行相互调运；各应急需求点关键性不同，关键度权重也不同；所有应急需求点的需要都能得到应急储备点的满足；应急储备点设立后不轻易改变站点选址。

在以上条件下构建轨道交通应急资源储备点选址模型。

3 模型建立

3.1 模型主要约束条件

在模型建立之前，需对模型的部分需要约束的问题进行说明：

1) 需考虑应急救援速度最快，并且需最大满足应急需求点的需求。

2) 在设置关键度权重时，关键度越高的需求点所得到的应急储备点的服务与支持越多。

3) 保证每个需求点至少有一个应急储备点提供服务。

4) 设置应急储备点到应急需求点之间的反应时间的约束。

5) 从总体设置条件与成本考虑，需对应急储备点总数进行约束。

3.2 多目标的应急资源储备点选址模型

根据以上分析，构建得出多目标应急资源储备点选址模型如下：

1) 建立目标函数。首先应当确立的各个应急储备站点到到各需求点的距离以及在加权下的应急反应时间的距离最小。目标函数式(1)如下：

(1)

式(1)中，α1和α2为权重系数；i∈I，I={1,2,3,…,n}为所有应急需求点的集合；j∈J，J={1,2,3,…,m}为所有潜在应急资源储备点的集合；Pi为应急需求点i的关键度权重系数；dij为应急需求点i到应急资源储备点j的距离；rj为应急资源储备点的服务半径。

其次我们需要使得关键度越高的需求点得到越多的储备点的服务越多；qi为应急需求点i被重复覆盖次数。目标函数(2)如下：

(2)

在上述条件下，应当考虑应急需求点的最大化收益值。Vi为应急需求点所影响的客流人数，以日均客流为基准；ui为应急需求点i可能发生应急事件的概率；uij为应急资源储备点覆盖到应急需求点i的概率；yij为{0,1}变量，当应急资源储备点j覆盖到应急需求点i时，yij=1；当应急资源储备点j没有覆盖到应急需求点i时，yij=0。表达式如下：

(3)

最大化收益目标函数式(4)如下：

(4)

2) 约束条件建立。首先应当使得全部的应急资源储备点到其所需服务的应急需求点的距离满足其服务半径的要求。cj为第j个应急储备站点所服务的需求点的个数。约束条件式(5)如下：

maxdij=rj, 1≤j≤rj

(5)

对于应急储备点服务半径的取值约束如式(6)所示：

(6)

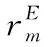
若j点为应急资源储备点，则最多可服务n个应急需求点，即：

(7)

要求满足每个应急需求点至少有一个应急资源储备点提供应急服务，约束如式(8)：

(8)

由于综合成本等原因需对应急资源储备站最大数量进行约束，设置最大数量为s，约束如下：

(9)

在应急反应时间方面，应急资源储备点j出动资源到达应急需求点i的反应时间不能超过轨道交通应急救援的临界时间值tc；wij为应急储备点到应急需求点的平均速度，因此平均时间表达式为

(10)

则应急反应时间约束式：

(11)

在约束变量中，xj为{0,1}变量，当在j点设置应急储备点时，xj=1；反之，则xj=0。

(12)

4 算例分析

上文所建立的模型为多目标线性整数规划模型，采用Matlab算法工具，使用遗传算法进行求解。由于在约束条件中出现不等式约束，因此可考虑采用松弛变量将约束条件转化。综合考虑本文所建立模型，采用线性加权和法，现将多目标问题简化成单目标问题进行函数求解。目标函数综合表达式为

(13)

算例中假设应急需求点为24个，候选应急资源储备点为8个，如图1所示，因此I={1,2,3,…,24}，J={1,2,3,…,8}。在本实例中，需在8个候选应急储备点中选取6个作为最终的应急资源储备点。假设所有应急事件发生的可性能相等，所有资源储备点提供应急服务的可能性也相等；假设应急储备点的服务半径一定，本算例中设定为服务半径6 km；同时对轨道交通应急资源储备点资源物资出动的平均速度进行设定，根据轨道交通救援车辆的速度平均设定为vij=30 km/h；根据轨道交通抢修时间阈值界限，设置应急反应临界时间为tc=15 min。

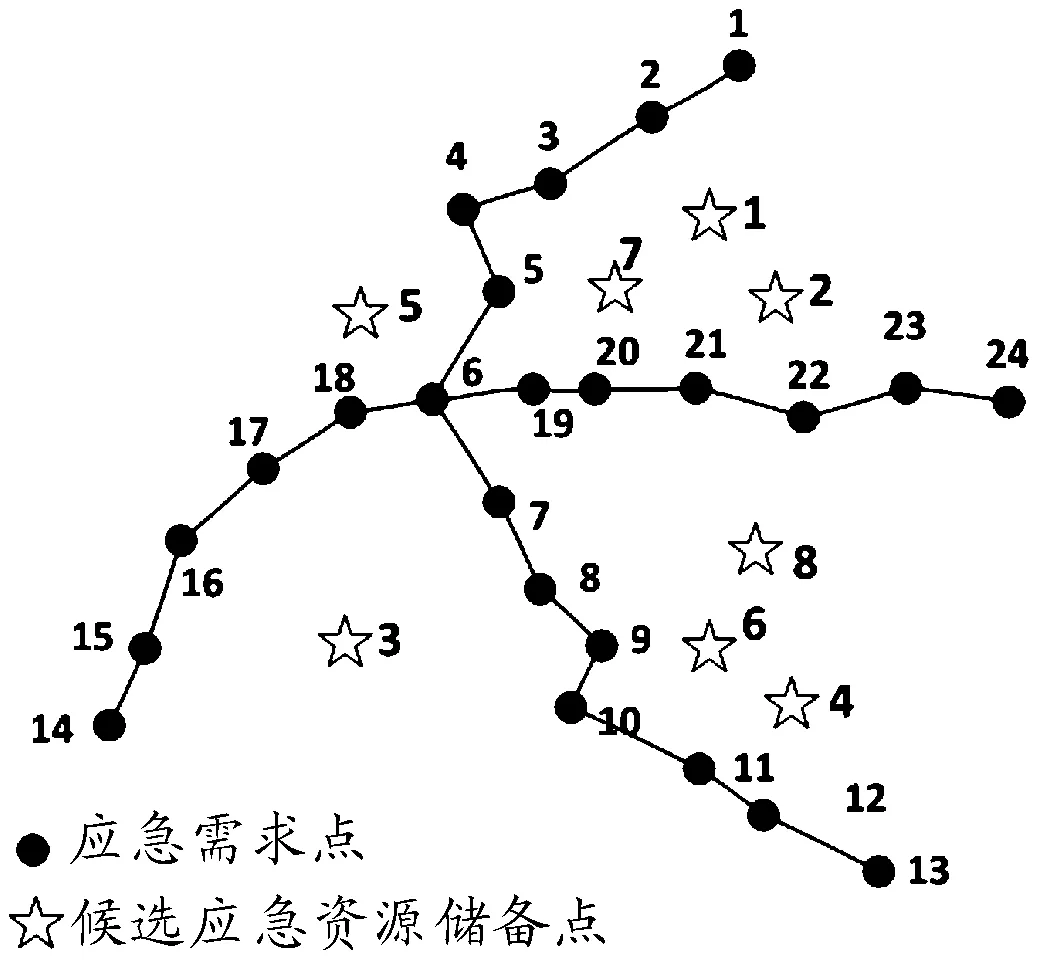
图1 应急需求点与候选应急资源储备点位置图

给定应急资源储备点与应急需求点之间的关系如表1所示。例：应急资源储备点j=1可覆盖i=1，i=2，i=3，i=22，i=23，i=24共6个应急需求点。

表1 应急资源储备点与应急需求点之间的关系

在应急需求点关键度权重上，通过评估需求点客流量，需求点周围环境包含的危险因素，以及对危险因素的应对控制能力来进行关键度权重pi的确立。

(14)

式(14)中：f为潜在危险因素数量；f1为危险发生临界值；g为单个站点客流量；g1为所有站点总客流量；T为风险控制能力水平值。由此可得各站点关键度权重系数pi。日平均客流和权重如表2所示。

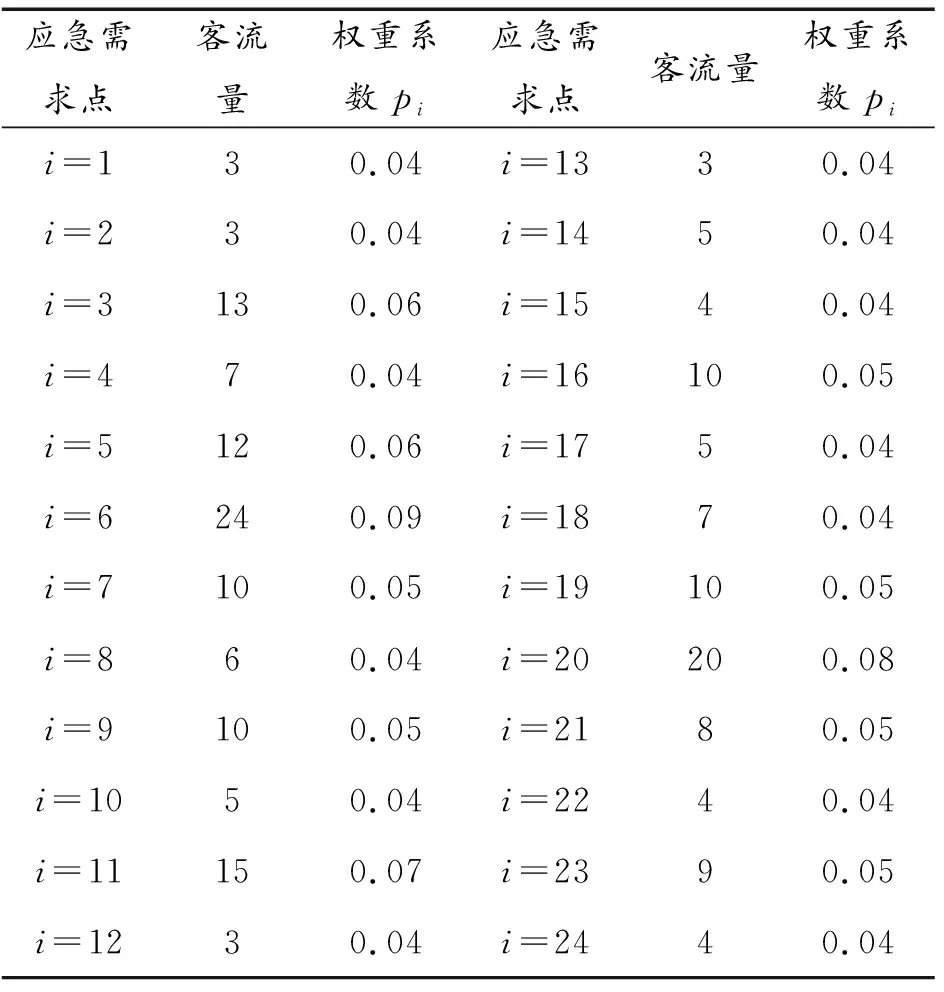
表2 各应急需求点客流与权重系数

给定各轨道交通应急物资储备点到各应急需求点之间的距离dij如表3所示。

表3 应急资源储备点到应急需求点之间的距离

根据第二章所建立的多目标规划模型求解可最终得出应急资源储备点选址为j=1，j=3，j=5，j=6，j=7，j=8共6个点，覆盖图如图2所示，6个储备点所最终覆盖的需求点情况如表4所示。

图2 筛选的应急资源储备点与所覆盖的需求点

被覆盖频次应急需求点1次i=1,i=2,i=4,i=8,i=10,i=12,i=13,i=14,i=15,i=17,i=18,i=21,i=22,i=242次i=3,i=5,i=7,i=9,i=11,i=16,i=19,i=233次i=6,i=20

根据所得6个应急储备点覆盖的需求点情况，可得出各需求点的实际覆盖频次。

分析可以得出：关键度权重高的应急需求点所得到的覆盖频次越高。算例中，i=6，i=20两个权重值分别为0.09和0.08的高权重需求点均得到了3次覆盖；权重值居中的部分需求点得到了2次覆盖，如i=7，i=9这两个权重值在0.05的需求点；而权重值低，本算例中pi=0.04的关键度较低的站点则满足了至少覆盖1次的要求，如i=1，i=2等。同时可以看到，例如i=11等pi=0.07高权重需求点只获得2次覆盖，并没有与i=6等站点一样获得3次覆盖，由此可见，模型考虑了应急储备点设置的合理性、经济型、有效性等方面的因素，满足实际的需求。

5 结论

城市轨道交通的应急系统与应急响应至关重要，而做好轨道交通应急资源储备点的选址与优化对于有效应对轨道交通突发事件有着积极的影响。在以往对于应急储备的选址问题研究中，对于应急事件、经济成本等方面因素考虑较多。鉴于轨道交通的特殊性以及轨道交通重要节点对于全网的关键性，本文综合考虑了应急需求点的关键度权重，从而使得关键节点能够获得尽可能多的应急资源储备点的覆盖。本文建立了多目标规划模型，并最终验证了高权重的站点获得了较多覆盖，并同时兼顾了站点设置的经济性、合理性、有效性。