基于颜色Petri网的食堂窗口排队模拟仿真

邓雪峰 侯益明 冯灵清

摘   要：食堂窗口是高校中排队现象最普遍的服务窗口，在就餐高峰期容易出现排长队的情况。文章对高校食堂的4个服务窗口进行了实地的调查，发现高校食堂窗口的平均到达率为1.3，平均服务率为0.672 413 793，平均队长为3.741 935 485，在此基础上，利用CPN Tools工具对食堂的排队情况进行动态仿真与监测。经实验证明，在可控制的误差范围内，该模型可以有效地对高校食堂的排队情况进行模拟仿真。

关键词：颜色Petri网;食堂窗口;CPN Tools

随着中国教育规模的扩大，高校的各项服务设施的流程优化可以提升服务窗口的服务效率，从而满足日益增长的消费需求。在大学的服务设施中，食堂是一个重要的服务窗口，食堂的排队乱一直是大学食堂广泛存在的现象[1-2]，在就餐高峰期如何优化排队、提升食堂的服务效率一直是一个值得研究的问题。

排队论是一种对排队现象进行分析的数学方法，排队论的思想已经用于多种领域，如计算机系统[3]、物流管理[4]、医院管理[5]、通信系统[6]、远程服务系统[7]等。排队系统同样也可以用于对食堂排队现象进行分析。排队系统的仿真可以模拟研究当前排队系统的相关特性，动态地模拟排队过程，有助于分析排队系统的性能[8]。颜色Petri网[9]（Color Petri Nets，CPN）是一种形式化的建模方法，通过CPN可以简化建模过程，并且可以利用CPN Tools等工具对模型进行仿真运行。本文利用颜色Petri网对食堂排队系统进行建模并仿真，根据食堂的排队实际数据模拟出食堂的排队情况，从而为食堂排队窗口的优化管理提供一种模拟仿真的方法。

1    食堂排队过程

1.1  食堂排队系统的组成

一个排队系统一般由系统的输入过程、系统的排队规则以及系统服务窗口的服务方式组成。一个典型的食堂排队系统如图1所示。

食堂排队系统的输入过程是一个随机的过程，一般来说，食堂就餐顾客的到达服从指数分布，到达每一个服务窗口的顾客服从泊松分布，食堂排队系统的排队方式一般服从先来先服务的原则。

1.2  食堂排队系统的服务流程

食堂排队系统的一般流程为：食堂的排队分为有排队情况和无排队情况两种，当顾客当达时，如果有排队的队列，则到达的顾客服从先来先服务的原则，到队尾进行排队，等待队列前无顾客进行服务，当顾客到达时，如果没有排队的现象，则直接穿过空队列进行服务，此时，不存在排队模型，因此，也无需进行优化。当顾客到达较为密集时，将会出现排长队和等待时间过长的问题，此时，就需要根據实际情况进行窗口的设置与排队系统的优化。

2    食堂排队系统建模

2.1  颜色Petri网简介

颜色Petri网是一种以Petri网为基础发展起来的高级网络系统，与谓词Petri网有着同样重要的作用，可以对离散的事件进行模拟仿真，并进行性质分析及状态空间的分析。颜色Petri网定义为六元组∑=（P，T;F，C，I，M0），（P，T;F）为有向网，为∑的基础网;C为颜色集，在本文中采用了赋时颜色集、整数颜色集等颜色集;I分为I﹢和I﹣，代表P×T是正函数和负函数;M0代表托肯色。

2.2  排队系统模型建立

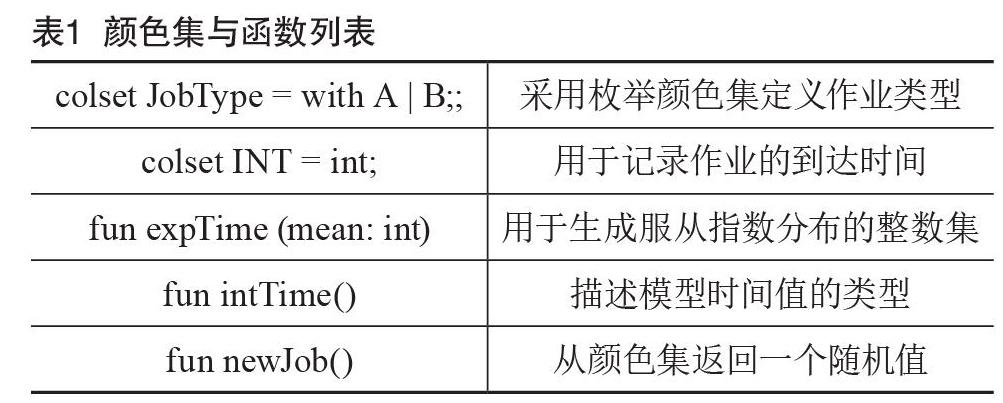
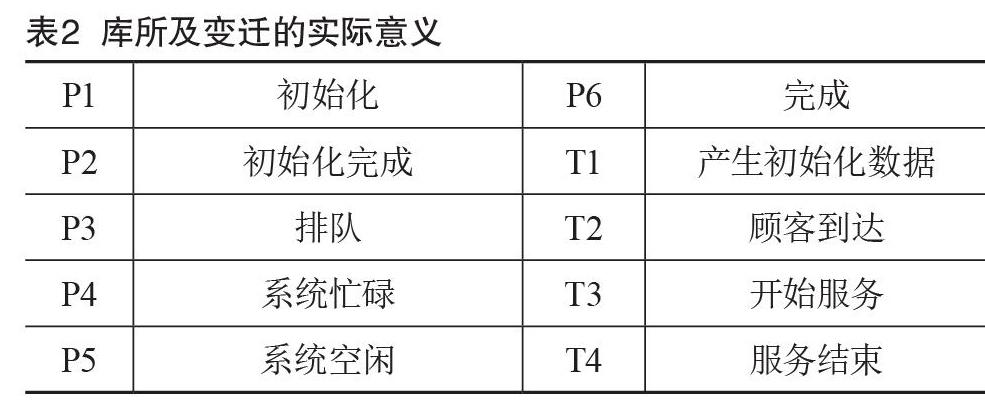
排队系统的模型有到达和服务两部分。（1）到达部分：由P1，P2，T1，P3，T2组成;（2）服务部分：由P6，P3，P4，T3，P5，T4组成，P3是排队状态，属于到达与服务的分界线，在本系统中用到的颜色集部分及函数如表1所示。

食堂排队系统的模型如图2所示，其中，P1—P2产生服从于作业到达情况的随机数;在P2—P3过程中，进行队列的排队过程;当系统处于P4空闲时期时，到达的作业直接进行服务;当系统处于P5的忙碌时期时，到达的作业根据先来先服务原则到队尾进行排队;直至系统处于P4的空闲时间进行服务，通过T4服务完成。表2阐述了每一个库所和变迁的实际意义。

3    排队系统模型模拟分析

3.1  模拟

在高校的食堂中，用餐高峰期，各个食堂窗口前会有学生排成长队等待打饭的情况，许多同学打饭时选择就餐的饭菜是由哪个窗口排队的人比较少决定的，有的队伍会出现打饭时间过长的问题。本文通过对某高校的食堂的排队情况进行实地调查，以1 min为单位时间，以4个窗口为调查对象，发现高校食堂很少存在学生排队过程中离去的状况，即窗口顾客的损失机制几乎为0。通过监测发现，高校食堂窗口的平均到达率为1.3，平均服务率为0.672 413 793，平均对长为3.741 935 485。在不考虑插队和损失的情况下，对高校食堂排队的队长进行约1 h的模拟，一般高校中午的就餐高峰时间约为1 h，队长的模拟情况如图3所示，CPN Tools可以通过颜色集及时间戳的方式对该模型进行有效的监督，动态性地证明了该模型的有效性。

3.2  分析

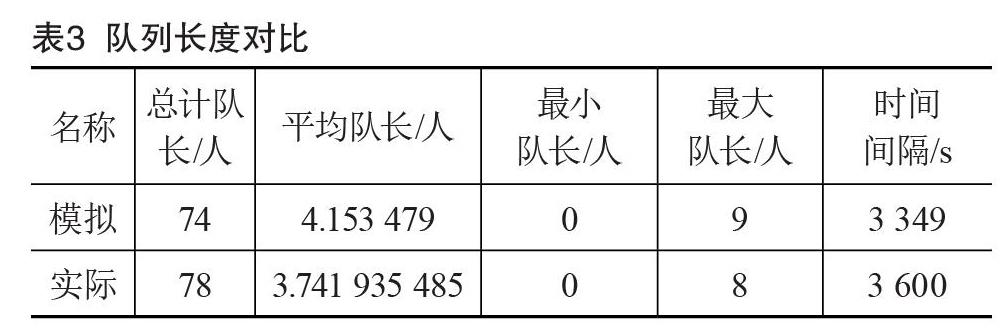
通过对模拟情况与实际情况的对比分析得到表3，通过表3得出，模拟总计队长74，实际总计队长78，队长总和相差4人，误差总队长占实际总队长的5.1%，模拟平均队长4.153 479，约4人，实际平均队长3.741 935 485，约4人，在可控的误差范围内，该模型可以有效地描述高校食堂的排队模型。

4    结语

本文通过颜色Petri网对食堂的排队模型进行建模并利用CPN Tools工具对高校食堂的排队情况进行模拟，将排队论的理论模型有效地应用于食堂的排队系统中，并对食堂的排队情况进行动态的仿真。仿真实验结果表明，本方法可以对食堂的排队情况进行有效的仿真模拟，可以利用仿真的结果为食堂的管理提供排队情况的动态预测分析，从而更加方便、可视地对食堂窗口进行管理控制，最大限度地提高食堂排队系统的利用率。

[参考文献]

[1]李欣，肖芳园，杨牡丹.高校食堂排队模型的研究[J].现代物业（上旬刊），2012（10）：37-39.

[2]郝洵.学生食堂就餐动态过程的数学模型及仿真研究[J].武汉理工大学学报，2008（6）：20-22.

[3]佚名.基于排队论的级联交换机网络传输延迟分析[J].西北工业大学学报，2017（2）：40-42.

[4]张河山.排队论在集装箱堆场进场闸口管理中的应用[J].集装箱化，2017（10）：18-22.

[5]佚名.基于排队论的患者预约容量分配研究[J].湘潭大学自然科学学报，2017（2）：6-7.

[6]安然.基于排队论的数据通信网络性能优化[J].信息通信，2017（4）：5-6.

[7]暴希会，吴长奇，白桦，等.远程故障诊断系统的排队论分析[J].无线电通信技术，2007（3）：25-27.

[8]吴可嘉.蒙特卡洛法在解决食堂窗口排队问题上的应用[J].大连海事大学学报，2007（z1）：11-13.

[9]袁崇义.Petri网原理与应用[M].北京：电子工业出版社，2005.