一种求解旅行商问题的基于外部存档的自适应遗传算法

刘景鑫 李林林 李治华 张耘赫

摘  要： 旅行商问题是一类经典的组合最优化问题，在理论研究和实际应用领域具有重要的研究价值。本文提出了一种自适应遗传算法，通过变异率的自适应策略平衡算法的全局性和局部性，同时利用外部存档策略为种群进化提供具有全局指导信息的父代个体，提高了算法的收敛速度。通过对TSPLIB标准库中实例的测试，验证了算法的可行性和有效性。

关键词： 旅行商问题; 遗传算法; 自适应; 外部存档

中图分类号：TP301.6          文献标志码：A     文章编号：1006-8228（2019）07-51-03

Abstract： Traveling Salesman Problem is a classical combinatorial optimization problem， which has important research value in theoretical research and practical application. In this paper， an adaptive genetic algorithm is proposed， which balances the global ability and local ability of the algorithm by adapting the self-adaptive mechanism of mutation probability. An external archiving strategy is used to provide better parent individuals which have global guiding information for the evolutionary process， to improve the convergence speed of the algorithm. The feasibility and effectiveness of the proposed algorithm are verified by the test on the instances in TSPLIB standard library.

Key words： Traveling Salesman Problem; genetic algorithm; self-adaptation; external archiving

0 引言

旅行商问题是一类复杂的组合优化问题[1]，在理论计算机科学和运筹学研究中非常重要。问题易于描述但难以求解，是典型的NP难问题[2]。旅行商问题的目标通常是最小化总行程，而且所有节点都必须访问一次。旅行商问题可以被应用与各个领域，如电路板设计、无线传感器网络、交通网络、物流配送等领域[3-5]。求解旅行商问题的算法包括遺传算法、爬山算法、模拟退火算法、蚁群算法、禁忌搜索算法、粒子群算法等[7-10]。

1 遗传算法

遗传算法是一类最经典的基于种群的随机优化算法，它模仿达尔文生物进化论的自然选择和遗传学机理的生物进化过程。算法通过种群中个体的并行繁殖和选择，保留优良个体，得到新的下一代种群，通过这种优胜劣汰的自然选择不断的保留优秀个体，进而最终得到问题的最优解。遗传算法非常适合与求解排列组合问题。遗传算法的基本流程如下：

步骤1 初始化种群;

步骤2 评价种群中个体的适应值;

步骤3 对种群中的当前个体，利用进化操作生成新个体：

步骤3.1 从当前种群中随机选择2个个体;

步骤3.2 对2个个体利用交叉操作生成实验个体;

步骤3.3 对实验个体利用变异操作生成后代个体;

步骤4 重复步骤3直到终止条件满足。

对于遗传算法来说，最核心的部分就是选择合适的交叉算子和变异算子，其中交叉算子能够组合不同个体的基因，变异算子改变基因信息，进而改进种群的多样性，提高算法的全局搜索能力。选择和使用合适的交叉和变异算子，能够防止算法出现早熟收敛等问题，同时保持种群的多样性。本文在第二部分展示旅行商问题的模型，第三部分展示提出算法的结构，第四部分和第五部分给出实验和结论。

2 TSP旅行商问题

旅行商问题是所有城市节点搜索最短的汉密尔顿回路。描述方式如下：有N个城市，城市之间的距离用矩阵D=（dij）N×N表示，dij表示从城市i到城市j之间的距离，问题的目标是从所有路径中找到最短路径，如公式⑴，这是一种递归方式的表达，其中πi表示路径经过的第i个城市。一般TSP问题可以按照距离矩阵分为两类：对称性TSP问题和非对称性TSP问题。本文主要对常见的对称性TSP问题进行求解。

⑴

通常旅行商问题可以按照距离矩阵可以分为两类：对称性旅行商问题和非对称性旅行商问题。对称性旅行商问题是在一个带权无向完全图中找一个权值最小的Hamilton回路。在各类TSP中，该类问题的研究成果最多。近几年来，研究者或者基于数学理论构造近似算法，或者使用各种仿自然的算法框架结合不同的局部搜索方法构造混合算法。本文主要针对对称性旅行商问题进行研究。

3 基于外部存档的自适应遗传算法

3.1 个体编码

本文以城市序号为基因，对城市序号进行编码。由于旅行商问题要求最后回到出发城市，因此只需要对从出发城市到途径城市的序号进行编码即可。例如个体为{2，3，4，5，1}表示旅行商的线路为从2号城市出发，依次途径3号城市、4号城市、5号城市、1号城市，最后从1号城市返回2号城市。

3.2 交叉操作

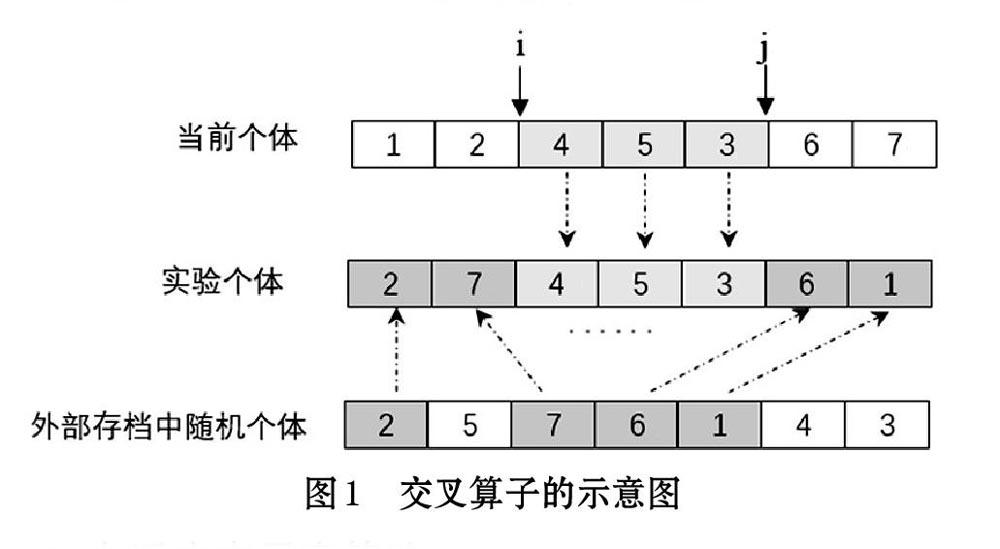
交叉算子是通过对父代个体的基因重组得到实验个体的过程。这里对LOX算子进行了改进，一般LOX算子父代个体的选择是来自当前种群中的随机个体，考虑到外部存档中的个体具有更高的质量，因此从外部存档中随机选择一个个体作为父代个体，另一个个体选择种群中的当前个体，在利用LOX操作的方式得到新个体。交叉算子如图1所示。通过这种方式，能够使优良基因信息在交叉过程中得到保留，使個体进化具有方向性，进而提高种群进化效率。

3.3 自适应变异率策略

变异操作是对生成个体的一个或几个基因位进行变化，防止个体的基因信息趋于相似而造成种群进化停滞现象。变异率的大小决定变异操作的机会的大小，变异率过大，会导致算法更加具有随机性，影响算法的收敛速度;变异率过小，会导致种群多样性变化太小，而出现早衰或陷入局部最优等问题。因此，为算法设置合适的变异率能够更好的平衡算法的全局探索能力和局部开采能力。

种群进化前期，算法更加关注种群进化的速度，因此需要设置较小的变异率来提高种群中个体的质量;随着种群的不断进化，算法容易出现多样性变差等问题，因此需要较大的变异机会才能够改变种群的多样性变差的问题。因此利用指数函数生成变异率，如公式⑵，其中为0.2。变异算子则采用随机交换交叉后生成个体的两个基因位的信息，得到新的后代个体，如图2所示。

3.4 选择操作

为了保存优良解，将后代个体与种群当前个体的目标函数值进行比较，如果后代个体的适应值优于当前个体，则利用后代个体更新种群中的当前个体。

3.5 外部存档

为了保存种群进化中搜索到的历史最好信息，将进化过程中生成的N个最好个体保存在外部存档中，用于种群进化的交叉操作。当新生成的后代个体更新种群的当前个体时，则将新个体与外部存档中所有个体进行比较，如果新个体比外部存档中的任意一个个体适应值好，则利用新个体替代原来个体。

4 实验

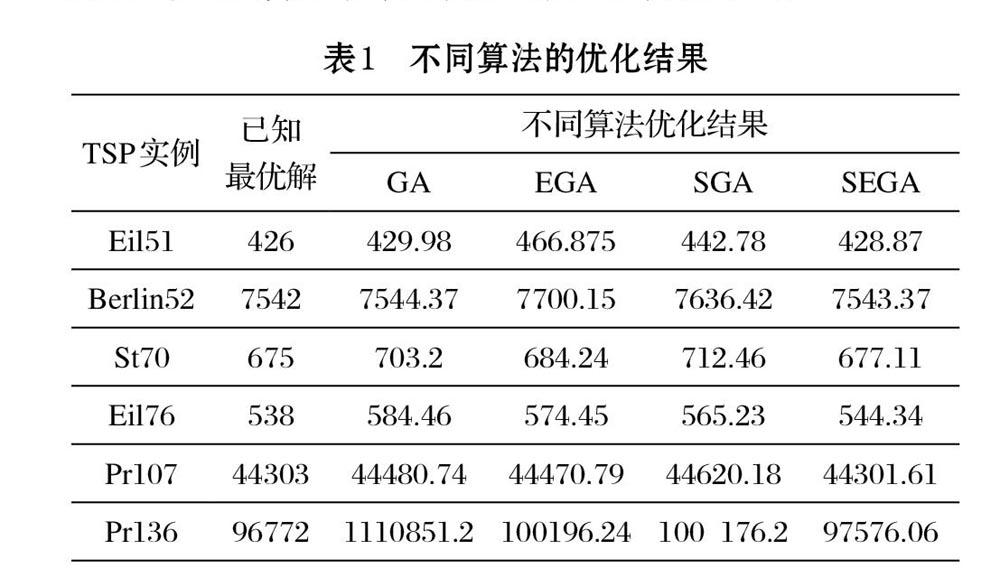
为了验证提出算法SEGA及策略的有效性，选取TSPLIB标准库中的Eil51、Berlin52、St70、Eil76、Pr107、Pr136六个实例进行实验。算法开发环境为Windows 8，使用Visual Studio2015进行开发，使用C++语言编写。算法的种群规模NP设置为100，自适应变异系数设置为0.2，外部存档最大容量N为10，算法的最大进化代数设置为10，000。对每个实例分别运行10次，得到的优化结果作为性能评价指标。本文将提出的算法SEGA与经典的遗传算法GA及不使用自适应策略的EGA和不使用外部存策略的算法SGA的优化结果进行比较，比较的结果如表1所示。

通过比较发现提出算法SEGA得到的结果均优于其他三种算法，说明算法提出策略是有效的。EGA算法不使用自适应变异率策略对旅行商问题进行求解，算法得到的结果6个实例中有5个实例比使用自适应策略的SGA算法的更差，二所有实例得到的结果均差于SEGA算法得到的结果，说明自适应的变异策略在平衡算法的全局探索能力和局部开采能力方面性能更好。SGA算法不使用外部存档策略，而外部存档策略能够为种群进化过程中提供更好的父代个体，帮助算法提高收敛性。从算法得到的优化结果来看，使用外部存档策略对于提高算法的收敛性是有效的。

5 结束语

本文提出了一种基于外部存档的自适应遗传算法，以对称性旅行商问题作为研究对象进行研究。通过对TSPLIB标准库中6个实例测试实验解结果对比分析，将提出算法与经典遗传算法及去掉自适应变异率策略、外部存档策略的算法进行比较，说明自适应变异策略在平衡算法局部能力和全局能力方面具有优越性，也证明了外部存档策略在提高算法收敛性方面的有效性。

参考文献（References）：

[1] PADBERG M W，RINALDI G. Optimization of a 532-citysymmetric genetic traveling salesman problems by branch and cut[J].Operation Research Letters，1987.6（1）：1-7

[2] GAREY M R， JOHNSON D S. Computers andIntractability：A Guide to the Theory of NP-Completeness[M]. New York： W. H. Freeman and Company，1979：56-59

[3] Kopanos G M， Puigjaner L， Georgiadis M C.Simultaneousproduction and logistics operations planning in semicontinuous food industries[J].Omega-International Journal of Management Science，2012.40（5）：634-650

[4] 潘颖，解晓宇，薛冬娟，谢忠东.全自适应遗传算法求解柔性作业车间调度问题[J].牡丹江大学学报，2014.23（3）：151-153

[5] 高立兵，苏军德.基于量子蚁群进化算法的大规模无线传感器网络目标覆盖研究[J].自动化应用，2018.10：53-56

[6] Lee W P，Hsiao Y T.Inferring gene regulatory networks using a hybrid GA-PSO approach with numerical constraints and network decomposition[J].Information Sciences，2012.188：80-99

[7] 王迎，张立毅，费腾等.求解TSP的带混沌扰动的模拟退火蚁群算法[J].计算机工程与设计，2016.37（4）： 1067-1070

[8] 王忠英，白艳萍，岳利霞.经过改进的求解TSP问题的蚁群算法[J].数学的实践与认识，2012.42（4）：133-140

[9] Grymin R，Jagiello S.Fast branch and bound algorithm for the travelling salesman problem[C]//Computer Information Systems and Industrial Management，2016：206-217

[10] 刘荷花，崔超，陈晶.一种改进的遗传算法求解旅行商问题[J].北京理工大学学报，2013.33（4）：390-393