求解TSP问题的改进模拟退火算法

何锦福 符强 王豪东

摘  要： 模拟退火算法是一种结构简单，鲁棒性强的群智能方法，在旅行商问题（Traveling Salesman Problem TSP）中得到了较好的应用。但是该算法在获取高性能解的过程中需要放慢降温过程，因此收敛速度较慢。为了解决该问题，本文对求解TSP问题的模拟退火算法进行了降温方式的改进，针对温度设置能量值，并根据能量值的高低状态判断是否进行跳跃式降温，从而在保证精度的同时，加快了算法的收敛速度。用TSPLIB标准库数据测试的结果表明，与改进前的模拟退火算法相比，改进的算法具有更加高效的寻优能力。

关键词： TSP问题; 模拟退火算法; 跳跃式降温; 二重退火

中图分类号：TP301.6          文献标志码：A     文章编号：1006-8228（2019）07-47-04

Abstract： Simulated annealing is a simple and robust swarm optimization method， which has been well applied in solving Traveling Salesman Problem （TSP）. However， the algorithm needs to slow down the cooling process in the process of obtaining high-performance solutions， so the convergence speed is slow. In order to solve this problem， this paper improves the simulated annealing algorithm for solving TSP， sets the energy value for the temperature， and judges whether the jumping cooling is carried out according to the state of the energy value， thus speeds up the convergence speed of the algorithm while ensuring the accuracy. The performance of the algorithm is verified by the test on standard TSPLIB data， the results show that the improved algorithm has a more efficient optimization.

Key words： TSP; Simulated annealing algorithm; jumping cooling; twice annealing

0 引言

TSP问题又被称之为旅行商问题，该问题为一名旅行商人要去多个城市旅游，其中每个城市仅去一次，且最终回到原点，求所走路径最短的方案。随着TSP问题中的城市数目增加，问题的复杂度呈指数上升，此类问题的大型实例无法用穷举法这类常规算法求解，需寻找有效的近似方法计算。目前人们已经提出了多种人工智能算法来求解该类问题：蚁群优化算法[4]，遗传算法[5]，神经网络算法[6]，改进的遗传混合蚁群算法[1]等。其中模拟退火算法使用灵活、描述问题简单直观，能扩大全局搜索能力，有效解决算法结果陷入局部最优的问题。因此在TSP问题的求解中具有更佳的性能。

模拟退火算法借鉴了固体退火的机制。当固体处于高温状态时，内部的粒子无序并且活跃，而在其慢慢冷却的过程中，随着温度逐渐下降，内部粒子将随之变得渐渐有序。1983年，S. Kirkpatrick等人成功将模拟退火思想引入到组合优化问题上。目前已经广泛应用于VLSI设计、一维下料问题研究[2]和神经网计算机的研究。在解决TSP问题时，模拟退火算法为得到精确的结果，耗费时间成本较大，本文由此改进了模拟退火算法的退火策略以达到保证结果精度的同时缩减时间的目的。

1 模拟退火算法

1.1 模拟退火算法简介

给算法一个初始值作为当前解，这个解包含的部分元素通过变换产生大量新解，算法选择其中的最优解作为当前新解。每一次都以最优解作为当前新解会让算法结果陷入局部最优，因此模拟退火算法有着概率突跳特性。即会以一定的概率去接受比最优解要差的解作为当前新解，那么下一次选择当前新解时就会在该差解的邻域空间中去寻找，这就为寻找全局最优解提供了新的方向，使算法跳出局部最优具有更大的可能性。模拟退火算法突跳性的概率会随着温度的降低而降低，在温度降低的同时算法重复着“产生新解→比较两个解的优劣→是否接受”的过程。当达到终止条件，算法所得的解即为全局最优解。

1.2 算法流程

Step1 初始化：设定初始温度T0，每个温度下的迭代次数L，给定初始解M。

Step2 每个温度下的L次迭代重复Step3-Step5。

Step3 产生新解MC。

Step4 计算增量ΔT=C（MC）-C（M），其中C（M）为评价函数。

Step5 若ΔT<0则接受MC成为新解，否则以exp（-ΔT/T）的概率接受MC作为新的当前解。

Step6 当算法满足要求或者达到终止温度时，程序结束。

2 基于改进模拟退火算法的TSP问题求解方案

在求解tsp问题时，模拟退火算法在初始温度、降温系数、终止温度、每个温度的迭代次数L共同作用下，算法进行大规模的数据迭代以及更新，搜寻比当前解更好的解，当达到终止温度后，算法运行结束得到的最新解就是最优解。模拟退火算法因为其大量的迭代次数以及概率突跳特性，拥有强大的全局搜索能力。但同时也需要大量的时间来完成算法的搜索过程。为了提升算法的效率，目前对模拟退火算法的改進方案大多是通过增加算子或与其他人工智能算法相结合等途径，来达到提高算法最优解精度的目的，而对于时间效率的考虑较少。本文对模拟退火算法的过程进行了探索，针对提高收敛速度的要求，提出了以下改进措施。

2.1 跳跃式降温

针对退火策略提出跳跃式降温，每一个温度都有能量值P。在某温度下的L次迭代中，迭代成功的次数越多，则该温度的能量值P越大。给定一个能量标准值N，把此温度的P值与N值相比较，如果P值超过设定的N值，那么该温度被称为跳跃温度J。跳跃温度是指该温度在临近的温度当中，进行迭代的成功次数很多。可以进行一次跳跃式降温，把该温度临近的温度所需要进行的降温环节省略，进行一次幅度比较大的降温。在算法使用跳跃式降温后，相比没有使用跳跃式降温的算法，数据迭代处理的次数大大减少。

2.2 二重退火

跳跃温度分为基准跳跃温度JR和超级跳跃温度JS。JR代表P值略大于或等于N值。JS代表P值远远大于N值。在JS 中能搜寻到的最优解质量是远高于JR中得到的解。在判定某个温度为JR后进行了跳跃，如果该温度的临近温度中出现了JS，那么JS就会被跳过。这种情况下就遗漏了这附近所有温度中所能得到的最优解。为了尽量消除这种情况带来的影响，算法还使用了二重退火。利用第一次退火产生一个较优的解，然后把温度初始化。开始进行第二次退火，产生一个最终解。进行第二次退火等价于让第一次退火中产生的较优解重新回到高温状态下去迭代。第二次退火中，初始解的精确度已经较高了，因此退火过程中整体的迭代成功率下降。原来的JR退化成了普通温度，而JS相较之下则更可能被保存下来仍然被判定为跳跃温度，进行跳跃式降温。这样就更容易搜寻到最优解，解决了JR与JS出现位置相近带来的问题。算法使用跳跃式降温与二重退火的改进后，相比其他文献，在保证了结果的精确性的基础上又减少了数据迭代处理次数。

2.3 路径的变异方式

路径变异方式的多样性影响到全局解是否会陷入到局部最优。在产生新路径的时候，如果只用一种路径的变异方式，那么新的路径产生就只朝着该变异方式的方向进行下去，即使模拟退火算法以一定概率接受较差解来跳出局部最优解，所能达到的也只是该种路径变异方式下的全局最优解。多增加几种路径的变异方式，新路径的产生就能从多个方向去进行，此时就会有更大的可能去逼近标准的解。本文采用了交换、移位、倒置的路径变异方式。

路径交换是指随机选择若干个城市进行交换位置。如果是两个城市之间的交换看成是点与点的交换。若干个城市点之间的交换，可以看成是城市点连成的城市段之间形成的交换。以此来形成新的路径。路径移位是指随机在路径中选出两个城市，把这两个城市以及它们中间的若干个城市，统一向左或者向右移动若干个位置，得到了新的路径。路径倒置是指随机在路径中选出两个城市，将这两个城市之间的城市顺序完全倒置得出新的路径。

2.4 改進后的算法流程

Step1 初始化：设定初始温度T0，温度下降系数A，终止温度Tf，每个温度下的迭代次数L，给定一条初始路径以及初始解。

Step2 每个温度下的L次迭代重复Step3-Step5。

Step3 用交换、移位、倒置的方式产生新的路径。

Step4 把新路径长度与原来的路径相比较，若新路径更短则直接替代原来的路径。如果新路径长则以“exp（-（Ln+1-Ln）/T）”的概率来接受新路径。（Ln+1为最新路径长度，Ln为原来长度，T为当前温度）

Step5 根据P值与N值得关系判断温度是否为跳跃温度。

Step6 降温。

Step7 达到终止温度Tf。算法运行结束得到结果。

3 仿真实验分析

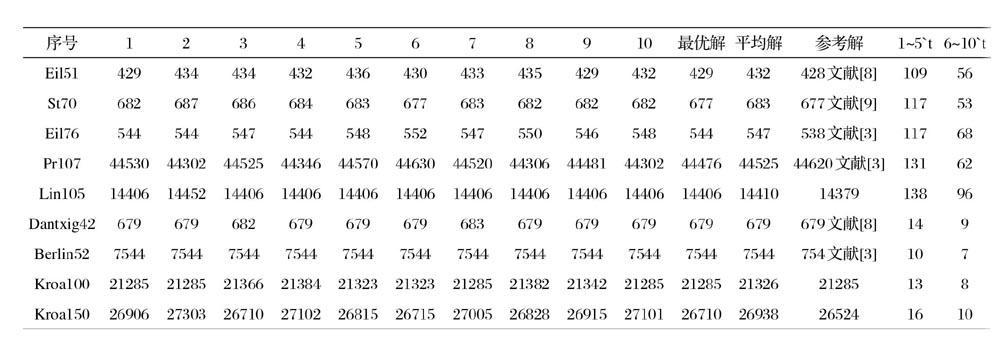
为了验证改进后的算法相比较于模拟退火算法在解决TSP问题时，在提高了收敛速度的同时还保证了解的精准度。该算法在TSPLIB标准库中随机选择不同规模的城市进行测试。为了保证实验不出现偶然性，针对每一个城市规模的TSP问题都进行十次仿真实验并采集数据。记录下最优解、计算出平均解，并以其他文献中的优秀解或官方解做参考。实验分别记录了每一个TSP问题的前五次算法平均运行时间和后五次的算法平均运行时间。每个问题的10次实验中前五次是没有改进降温机制的，后五次是使用了改进的降温机制。为节省篇幅，实验数据采用整数。

算法测试在Window 10系统core i7的环境下进行，测试的程序为MATLAB R2017b。每个TSP问题的实验初始温度为97?目标温度为3?迭代次数L为5000。eil51问题，st70问题，eil76问题，pr107问题，lin105的降温系数A为0.999，dantzig42问题、berlin52问题、kroA100问题、kroa150问题为0.99。从表中的平均值可看出本文算法的结果比较稳定，这是因为二重退火机制可以增强算法鲁棒性。实验数据中得到的最优解与参考解精度相近，从个别TSP问题中的到的最优解已经超越了参考解。从前五组与后五组的平均时间对比中可以得出在使用改进的降温方式以后，退火所需时间基本减少，加快了收敛速度。在针对城市数越多分布越复杂，降温越慢的情况上，效果更加明显。

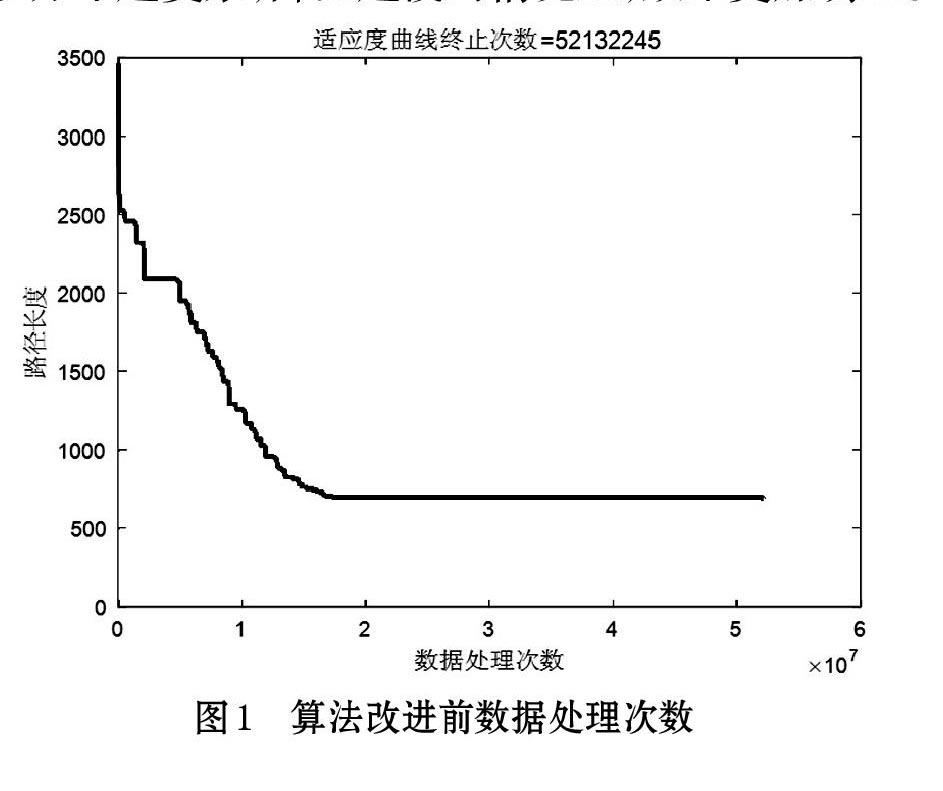
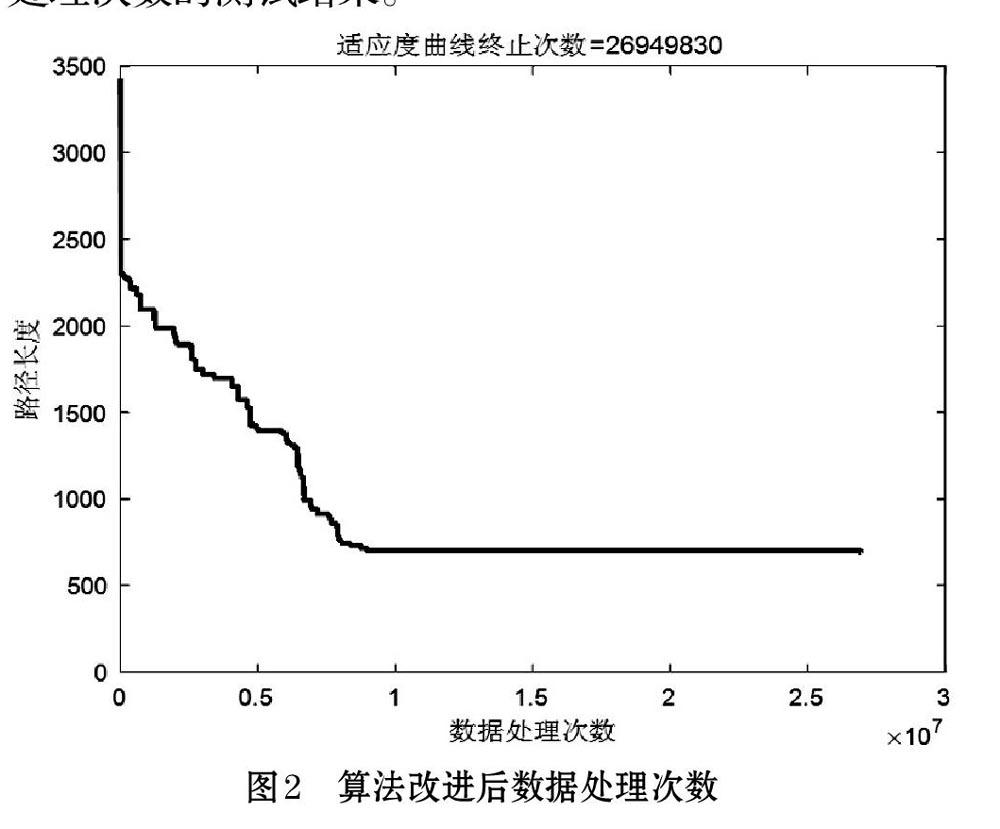
为了更好地展现改进后的模拟退火算法比改进前收敛速度的加快情况，本文记录并绘制了在不同城市规模下，各tsp测试结果的收敛曲线图。因篇幅的长度限制，这里仅显示st70在算法改进前降温系数为0.999（图1），以及改进后降温系数为0.999（图2）数据处理次数的测试结果。

在图1和图2两幅图中，曲线呈快速下降的趋势说明是高温状态。而趋于平缓则是已经到了低温期。从图中曲线的下降趋势可以看出，算法在改进前处理st70问题时，当数据处理1×107次时路径长度为1000～1500还处于快速缩短的过程。而算法改进后当数据处理1×107次时路径长度为500～1000已经处于平缓状态。图1的数据处理次数为52132245次，图2的数据处理次数为26949830次，减少了近一半的处理次数，因此花费时间也相应的缩短了一半，所得到路径长度是相近的。综上所述，本文改进后的模拟退火算法能够提高时间效率，节省时间。

4 结论

本文提出了一种改进的模拟退火算法，通过结合多种路径变异方式保证了解的精准度。创造了跳跃式降温的降温方式减少了运算时间。在保证算法寻找全局最优解能力的前提下，加快了从高温到低温的降温过程。使模拟退火算法的概率跳变特性更具有自适应性，利于算法寻优，并将改进的思想在程序中实现，通过对TSP不同实例的优化实验结果及对比分析表明，本文设计的算法具有可行性，可以为想要在模拟退火算法解的质量上做改进的同行，提供缩短算法运行时间的方法。该方法提高了针对TSP问题的优化效率，但是目前只对能量值做出一个定性的判定，下一步将对能量值做出一个定量的分析，使跳跃温度的判定更加准确。

参考文献（References）：

[1] 徐德明.改进的遗传混合蚁群算法在TSP问题中的应用[J].计算机时代，2012（11）：31-32+36.

[2] 张梦，陈仕军，李嘉宾，刘朝阳.基于模拟退火算法的一维下料研究[J].计算机时代，2017.12：1-4

[3] 杜鹏桢，唐振民，孙研.一种面向对象的多角色蚁群算法及其TSP问题求解[J].控制与决策，2014.29（10）：1729-1736

[4] 易正俊，李勇霞，易校石.自适应蚁群算法求解最短路径和TSP问题[J].计算机技术与发展，2016.26（12）：1-5

[5] 姚明海，王娜，赵连朋.改进的模拟退火和遗传算法求解TSP问题[J].计算机工程与应用，2013.49（14）：60-65

[6] 郭中华，金灵，郑彩英.人工神经网络求解TSP问题的改进算法研究[J].计算机仿真，2014.31（4）：355-358

[7] 张家善，王志宏.基于信息素的改进蚁群算法及其在TSP中的应用[J].数学的实践与认识，2013.43（22）：157-161

[8] 于宏涛，高立群，田卫华.求解TSP的离散人工蜂群算法[J].东北大学学报：自然科学版，2015.36（8）：1074-1079

[9] 程博，杨育，刘爱军等.基于遗传模拟退火算法的大件公路运输路径选择优化[J].计算机集成制造系统，2013.19（4）：879-887