发动机气门系统振动信号的多尺度分析
2019-08-06张森森蒋辉杨娟
张森森,蒋辉,杨娟
(1.中国人民解放军海军驻葫芦岛四三一厂军事代表,辽宁 葫芦岛 125000;2.沈阳天眼智云信息科技有限公司,辽宁 沈阳 110000)
1 引言
发动机作为一种重要的机械设备,合适的气门间隙是其正常工作的重要因素,然而气门间隙异常的情况经常出现。结合以往故障诊断实例来看,振动检测技术在实际应用中具有重要意义。本文通过分析发动机气门系统振动信号的方式,对其进行故障诊断。然而使用振动时间序列分析进行复杂机械系统进行的故障诊断,很难辨识该系统在可用状态和失效状态下的动力学模型,所以需根据车辆驱动系统的振动信号,分析车辆的非平稳特性和标度变量特性。
研究不同时间尺度下的实验数据集,基于分形统计方法进行动力学建模。由于被测信号的总特征是一个有关分析尺度范围的平均值,只了解单一标度指数是不够的。因此需要在考虑维数谱(奇点谱)的情况下,测量信号的多重分形水平,即由多个不同维数的交错分形组成的系统动力学。
由于计算方法相对简单,适用于数值计算,本文给出的计算结果是基于盒维数(体积维数)的。D 为时间序列的盒分形维数,假设曲线维数是所考虑信号的图谱。当与给定时间序列相一致的最小集合数为L,标度为s 时,。因此有:

自相似时间序列或积分后具有自相似性的时间序列描述了多重分形维数D(N),对不同标度范围的Hurst 指数H(N)有:

式中:N 是观测信号的样本数。
文献给出了基于多重分形(MF)的去趋势波动分析(DFA)算法。通过MF-DFA 算法计算Hurst 指数。与小波变换模极大值(WTMM)方法相比,MF-DFA 方法可以研究观测信号的多重分形,能够更稳定地处理多重分形形式。尽管MF-DFA 算法在故障诊断中有了较多应用,但尚未用于发动机气门系统。因此本文分析了发动机气门系统振动信号的脉动函数标度曲线和奇异谱,将信号的多重分形水平和奇异指数作为诊断特征,对发动机气门系统的所有模拟维修状态进行分类,验证了该方法在各种负载条件、转速和发动机温度下的有效性。
2 去趋势波动分析的改进
去趋势波动分析是研究标度指数和长程相关性,以及选择和分类复杂振动系统信号诊断特性的重要工具。
本文中的研究分2 个阶段进行。程序的第一部分是对波动函数进行尺度化处理,从信号中消除趋势,确定Hurst 指数;第二部分是对奇异指数进行Legendre 变换得到的多重分形谱。
假设观察到的时间序列xi 包含N 个样本。MF-DFA 过程如下:
(1)构造信号轮廓X(i),期望值为

(2)将信号轮廓X(i)以相同长度s 分成不重叠的Ns段数据。由于数据长度N 通常不能整除s,所以会剩余一段数据不能利用。为了充分利用数据长度,再从数据的反方向以相同长度分段,这样一共有2Ns段数据。
(3)利用最小二乘法拟合每段数据的多项式趋势,然后计算每段数据的方差:

式中,xv(i)为拟合的第v 段数据的趋势。若拟合的多项式为m 阶,则记该趋势过程为MF-DFAm。
(4)计算第q 阶波动函数的平均值:

(5)如果时间序列xi存在自相似特征,则第q 阶波动函数的平均值Fq(s)和时间尺度s 之间存在幂率关系:

式中,H(q)为长程相关性指数。如果xi是多重分形时间序列,则H(q)会随着q 的改变而变化;如果xi是单重分形时间序列,则H(q)是不依赖于q 的常数。当q=2 时,MFDFA 方法退化为DFA 方法。当q=0 时,式(6)发散,这时H(0)通过式(6)所定义的对数平均过程来确定:

指数H(q) 的统计可靠性评估需要在限制范围s ∈(10,N/4)内选择标度范围。当Hurst 指数值接近于零时,非持续信号的改进允许在MF-DFA 过程开始之前进行时间序列集成。对偶积分使数值波动函数的指数增加1,意味着
对于单分形,指数H(q)=const,而对于多重分形,指数H(q)=const 是一个递减函数。对于q 阶的负值,广义Hurst指数描述了低波动水平段的标度特性,而如果我们考虑q 阶的正值,则高方差段正在形成波动函数。根据广义Hurst 指数及下式所示的依赖关系,可以确定由奇异指数a 和奇异谱f(a)表示的局部标度,以此来表示广义多尺度指数τ(q)。
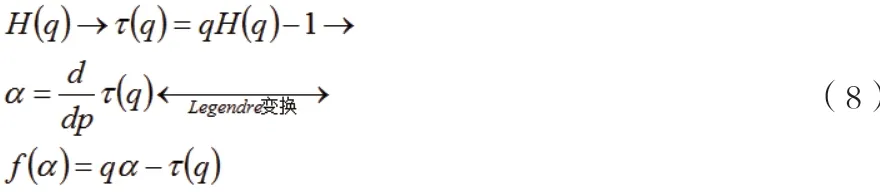
3 发动机气门系统多尺度诊断过程的实现
对M12 发动机进行了路试检查,对不同转速和负荷下的发动机振动进行了一系列测量。主要测量路径包括频率范围为0.1 ~16500Hz、共振频率为55kHz、工作温度为-74 ~+250℃的B&K4393 压电振动传感器(通过将接头拧入发动机侧的气缸1 处固定),以及用于记录数据的便携式设备B&K PLUSE 3560。在垂直和水平方向上记录发动机缸体振动的加速度,频率为65536Hz。然后用抗混叠滤波器对信号进行预处理,避免放大振动传感器固有频段中的分量。
除了发动机振动信号外,还记录了曲轴位置信号、节气门位置信号以及1 缸和4 缸点火线圈发出的信号。附加信号可以识别发动机工作周期、喷射力矩、点火和齿轮相位的正时。以恒定速度行驶时,记录1min 的持续信号。在进一步分析过程中消除了小的速度波动。由于发动机转速对振幅有很大的影响,因此在信号采集过程中,尽可能保证发动机转速恒定。负载对振幅影响较小,因此不作考虑。对振动信号重新取样,以均衡发动机每个运转循环中分析的样品数量。在分析过程中,该程序可以将时间域更改为曲轴的旋转角度。
检查气门系统的各种维护状态:
阀门工作状态良好,间隙最佳0.25mm(ZN);
阀门工作状态良好,间隙增0.06mm(ZNL);
阀门工作状态良好,间隙减-0.06mm(ZNL-);
阀门Ⅰ级故障(小缺陷),最佳间隙(ZU 小);
阀门Ⅱ级故障(大缺陷),最佳间隙(ZU 大)。
将M12 发动机2 个工作周期长度进行重新取样得到的集成信号(7200 个样本),分为相同长度的段。确定每一段的线性趋势,然后删除。
3.1 基于RMS 波动和交叉点的排气阀系统振动诊断特征提取
根据公式(5)确定无趋势积分时间序列的均方根波动。对长度为4 ~1024 个样本的时间尺度s 进行测量,以获得与时间无关的测量结果。在30 个时间序列中,确定了气门缺陷测试案例的平均波动与段(刻度)尺寸之间的关系。为了确定Hurst 指数,对双对数图中的曲线F(s)进行了3 个标度范围的直线逼近:6-64、64-128、128-1024。
第一个单列标度范围的特征是倾斜系数:0
3.2 基于奇异谱的振动信号特征选择与分类
为了提高精度并允许对所有模拟状态进行分类,在-5~+5 的顺序内,确定了通用Hurst 指数,并给出了相应的发动机气门系统的多尺度指数。这些算法步骤的平均结果如图1 所示。
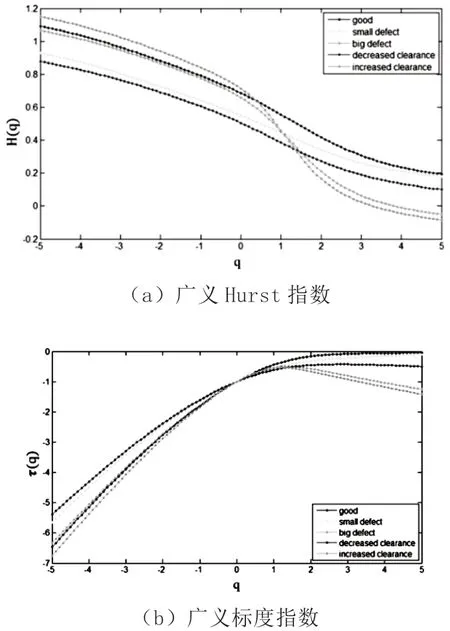
图1 测试维护状态的气门系统数据
分解结果得到的谱(图2)可以被视为与奇点相关的多重分形维数,表示测量在时间序列不同位置的局部比例。

图2 维修状态下气门系统振动信号的奇异谱
在调查中获得的曲线形状各异。利用基于多重分形水平建立的缺陷指数delta 对模拟维修状态进行分类,该指数代表被测信号的异质性。该特征定义为信号奇异性谱曲线的函数零点差。作为第二个特征,假设奇点指数A 为奇点谱的最大值。这是分析信号中最常见的奇点。与单个维护状态之间的分散相比,所选特性表示一个小的类间分散。图3 显示了列出的多重分形水平与奇点指数的关系图。
采用K-最近邻法对被测系统状态进行分类,并对分类质量进行分析。选择欧几里得平方距离作为度量,选择整数k=3。在精度评估中,采用了5 次交叉验证技术。分类准确度是根据正确分类的实验结果数量与总数量之比来评估的。
在每种维护状态下,进行相同系列的测试实验。每个测试观察生成100 个新的数据点,由选定的一对特征指定。将可用状态和所有模拟不可用状态分开。在500 个预测中,分类的混淆矩阵如表1 所示。
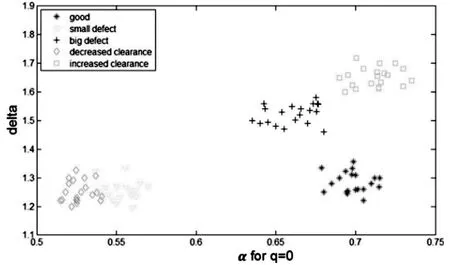
图3 多重分形水平和奇异指数的散点图.样本数据
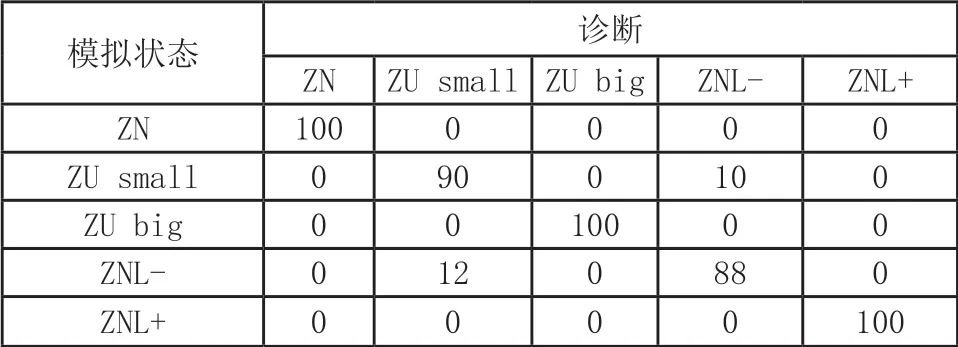
表1 用于发动机气门系统分级器的5 种维护状态的混淆矩阵
4 结语
分析了发动机气门系统振动信号的脉动函数标度曲线和奇异谱。根据Takens 延迟嵌入定理,该系统的所有其他动态变量都会影响该序列,所以采用一个变量的奇异时间序列。观察结果表明,在角度重采样之后,时间信号的比例曲线在维护期间发生了变化。振动信号中显示了标度变量特征。该变换过程是基于MF-DFA 算法,采用二次多项式进行离散。在分析的第一阶段,利用均方根波动和交叉点,验证了Hurst 指数是与信号的长程负相关,以及和相关性相对应的标度范围内的缺陷度量。该方法可以用来检测气门的初始缺陷和减小的阀门间隙。在大的气门缺陷和增加的气门间隙下,平面上的区域是弱可分离的,并且在缺陷的某个阶段,它们可能会重叠。研究的第二阶段包括从时间域到奇异域的信号转换。假设信号的多重分形水平和奇异指数作为诊断特征,从而对发动机气门系统的所有模拟维修状态进行分类。在线实验验证了该方法在各种负载条件、转速和发动机温度下的有效性。
