典型箱梁下腹板倾角对桥梁静风稳定性能的影响
2019-08-06姜保宋周志勇闫康健胡传新
姜保宋, 周志勇, 闫康健, 胡传新
(1.同济大学 土木工程防灾国家重点实验室, 上海 200092; 2.同济大学建筑设计研究院(集团)有限公司, 上海 200030)
大跨度桥梁在静风荷载作用下,主梁会发生弯曲和扭转变形.随着风速的提高,结构变形会进一步增大,当结构抗力的增速小于静风荷载增速时,结构发生静风失稳.随着桥梁跨径的不断增大,新型轻质高强复合材料的运用以及对桥梁美学的追求,桥梁结构变得更加轻柔,而桥梁静风稳定问题则日益突出[1].
对于跨度千米及以上的桥梁,由于结构刚度的降低,静风失稳可能先于颤振失稳出现.日本东京大学Hirai教授于1967年在悬索桥的全桥气弹模型风洞试验中观察到了静力扭转发散的现象[2],同济大学在对汕头海湾二桥的风洞试验中,发现了斜拉桥由静风引起的弯扭失稳现象[3].静风稳定性是千米级桥梁抗风性能的主要考查指标之一,因此,深入研究千米级桥梁的静风稳定性显得尤为重要.
由于桥梁的风荷载主要作用在主梁上,桥梁主梁气动力是决定桥梁静风稳定性能的主要因素.而桥梁主梁断面气动外形影响气流遇到断面以后的流场分布,直接决定了作用于主梁上的风荷载大小,即主梁三分力的大小,进而影响了桥梁的静风稳定性临界风速.
扁平箱梁由于风嘴的存在,可近似看成流线型结构[4],Sarwar等[5]研究了B/D=11.6(B为主梁宽度,D为主梁高度)情况下的流程及气动力分布,当风嘴角度为51°时,其气动性能类似于B/D=20的矩形断面.不仅如此,风嘴的外形参数对桥梁涡振响应也有着显著影响.Larsen等[6]的研究表明,通过改变闭口箱梁下腹板倾角,可以有效降低桥梁的涡振响应.Larsen同时指出,通过控制下腹板与水平底板夹角在15°以内,可以有效地将涡振振幅控制在较小的范围之内,甚至无涡振.孟晓亮等[7]的研究表明,封闭钢箱梁和半封闭分离双箱梁断面采用较小的风嘴角度,可以改善此类主梁断面斜拉桥的涡振性能,且较小的风嘴角度基本不会对桥梁的颤振稳定性产生不利影响.
以上研究表明,风嘴可以有效降低流动过程中的分离[8],从而减小作用于主梁上的气动力,提高主梁的抗风稳定性能[7-9].较小的风嘴角度有利于提高桥梁的颤振及涡振稳定性能.但是必须选取合理的风嘴角度,才能有效改善主梁的气动性能.同时,上述研究主要是针对风嘴对桥梁颤振及涡振性能的改善方面,其对桥梁静风稳定性能的改善及机理方面还缺少相应的研究.而计算流体动力学(CFD)方法目前在桥梁颤振机理分析、颤振临界风速预测、断面选型、抑振措施优化等方面均有成功的应用[10-13].通过CFD技术的应用,极大地提高了桥梁断面选型效率及计算准确度,可以说已经成为桥梁断面气动优化选型及机理分析的一种可信及重要的手段.
本文以大跨桥梁中常用的近流线型箱梁断面为研究对象,通过CFD方法,选取下腹板倾角这一关键几何参数,研究箱梁断面在不同下腹板倾角下的静气动力特征,并从流场的角度对其机理及差异进行分析.在上述CFD计算基础上,在不考虑主梁结构外形改变对刚度影响的前提下,选取一2×1 500 m的斜拉桥为加载模型,对比分析斜拉桥在不同腹板倾角下的静风稳定性能,并从三分力系数及桥梁失稳形态解释其失稳机理.
1 CFD数值模拟
1.1 断面选取
桥梁主梁气动力对于几何外形较为敏感,不同几何外形下,桥梁的静力三分力系数差异明显.本文通过CFD数值模拟技术,选取下腹板倾角αD(箱梁下侧腹板与水平底板之间的夹角)这一关键几何参数进行研究,分析其静气动力特征及流场分布的变化.断面如图1所示.考虑到大跨桥梁的宽高比多在10左右,断面的宽高比选为10,断面宽度为4 340 cm,断面高度为434 cm,桥面横坡为3%;参照He等[16]的研究结果,风嘴距下缘与上缘高度比应控制在2~3以内,本文选取2.86,风嘴距上缘高度为96 cm,距下缘高度为275 cm,上腹板倾角为50°,下腹板倾角变化为8°~50°.

图1 计算断面(单位:cm)
1.2 计算域及网格尺寸
网格划分采用ANSYS ICEM CFD软件进行.计算区域参见图2(B为主梁宽度、D为主梁高度),数值风洞高度为30D,进口距桥梁断面中心为5B,出口距桥梁断面中心为10B.采用结构化网格进行划分,通过块划分技术合理控制网格的疏密分布.桥梁断面壁面Y+分布见图3,满足Y+<5的要求.采用基于二维雷诺时均的k-ωSST((shear stress transport))模型进行流场计算.计算模型比例选取为1∶100,共计算了下斜腹板倾角αD在8°~50°变化范围内共43工况(角度步长为1°)、-12°~+12°共25个风攻角下的三分力系数.



图2 网格划分及数值风洞尺寸
Fig.2Dimensions and meshing of numerical wind tunnel

a αD=15°,α=-12°

b αD=50°,α=-12°
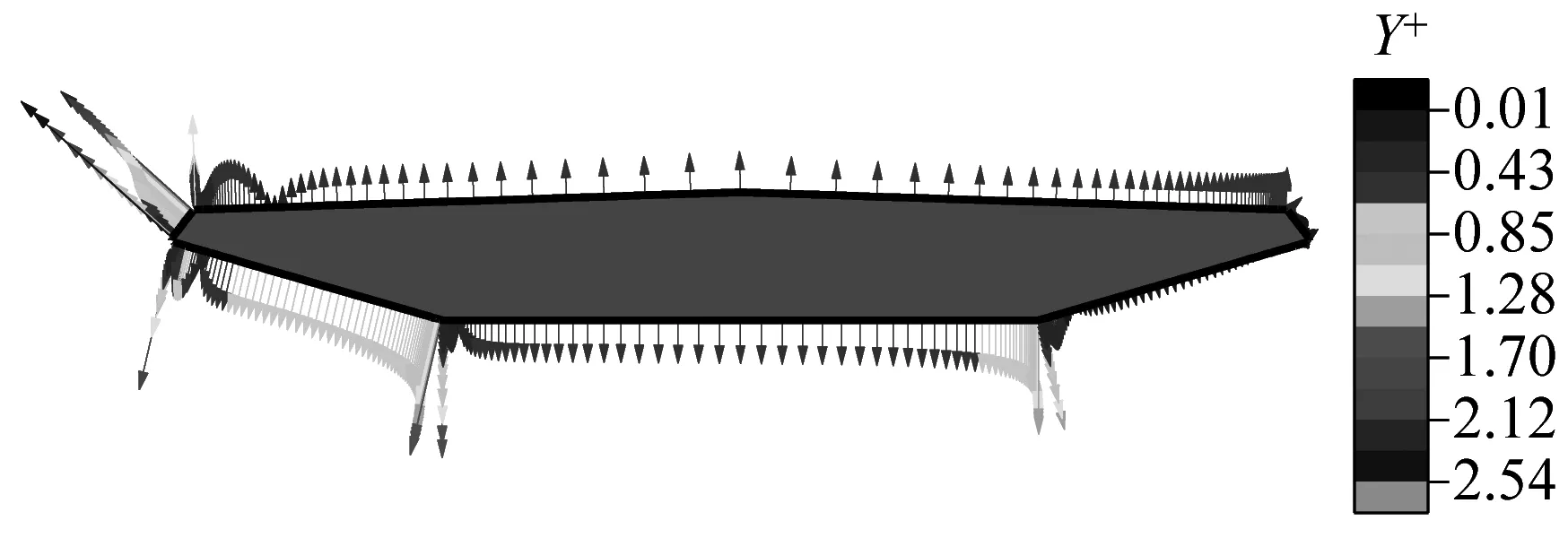
c αD=15°,α=0°
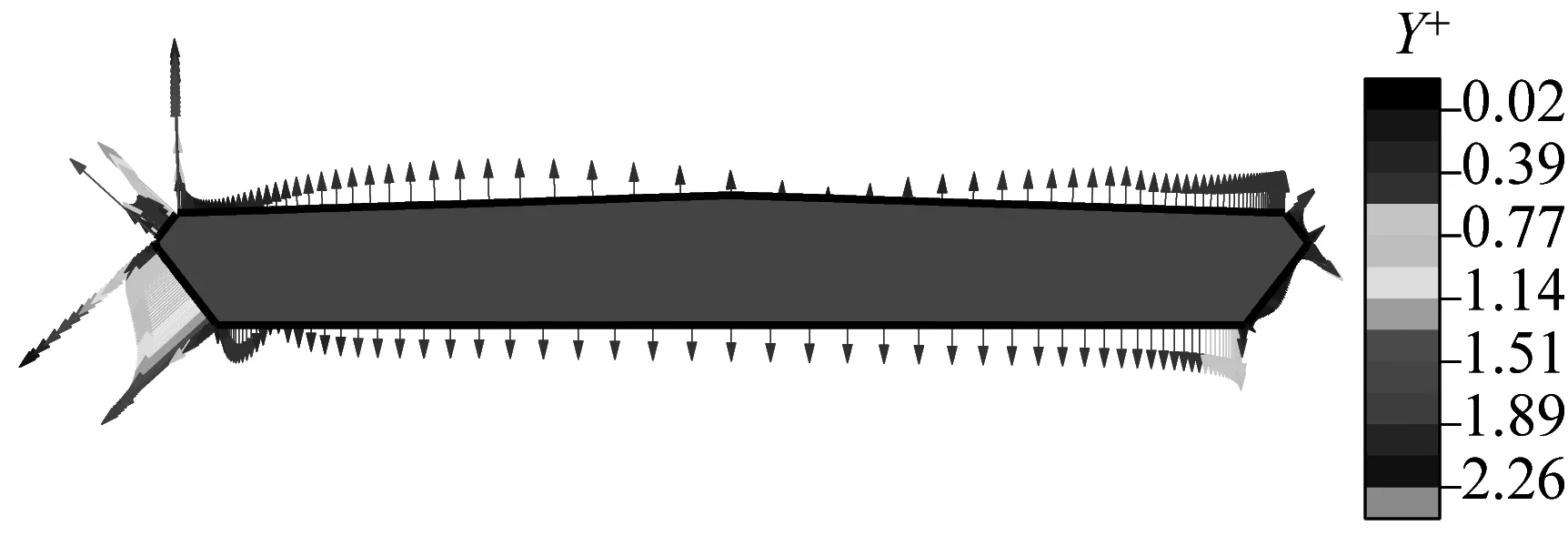
d αD=50°,α=0°

e αD=15°,α=12°

f αD=50°,α=12°
图3 桥梁断面壁面Y+值分布
Fig.3Y+distribution on wall of bridge section
如图4所示,FD、FL、MT分别为风轴坐标下单位长度作用于主梁的阻力、升力及扭矩;FH、FV、MT分别为体轴坐标下单位长度作用于主梁的阻力、升力及扭矩;α为风攻角;主梁三分力系数定义如下:
CD=FD/qWD
(1)
CL=FL/qWB
(2)
CM=MT/qWB2
(3)
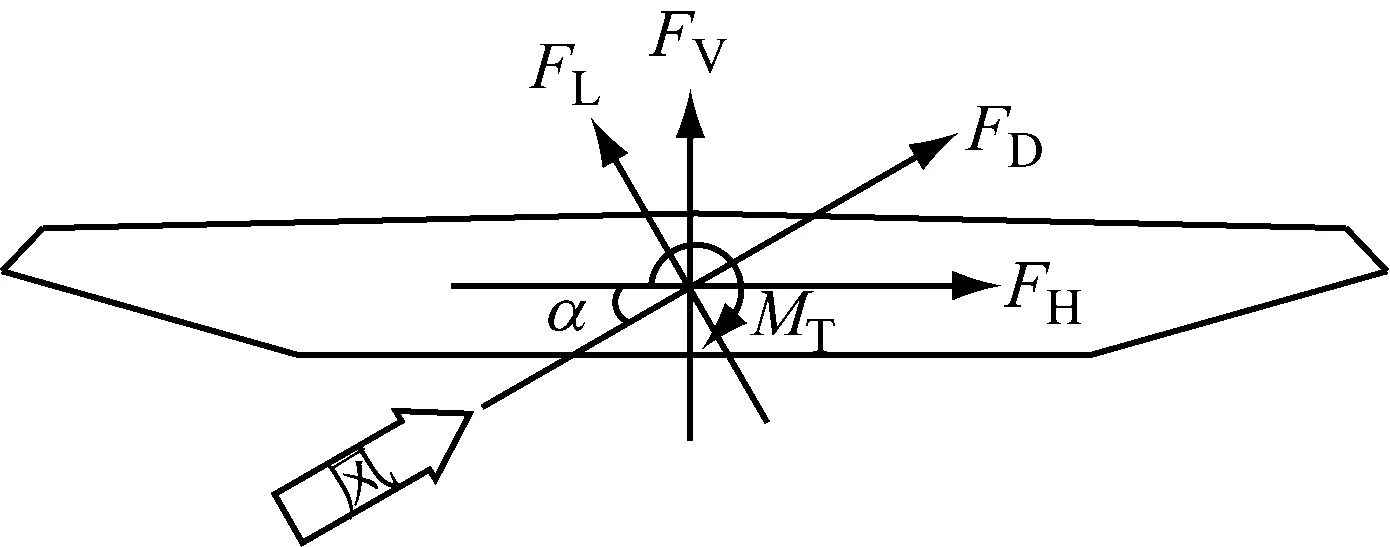
图4 风荷载坐标系统示意图
1.3 三分力系数
1.3.1阻力系数
箱梁断面的阻力系数随αD及风攻角的变化如图5所示.对不同的αD,CD随风攻角的变化趋势一致:在α=-5°~5°范围内的变化较为平缓,均在0.8以下;在α=-5°~-12°及α=5°~12°范围内的阻力系数变化明显.在12°攻角下,CD>2.3,在-12°攻角下,CD>1.8.

a
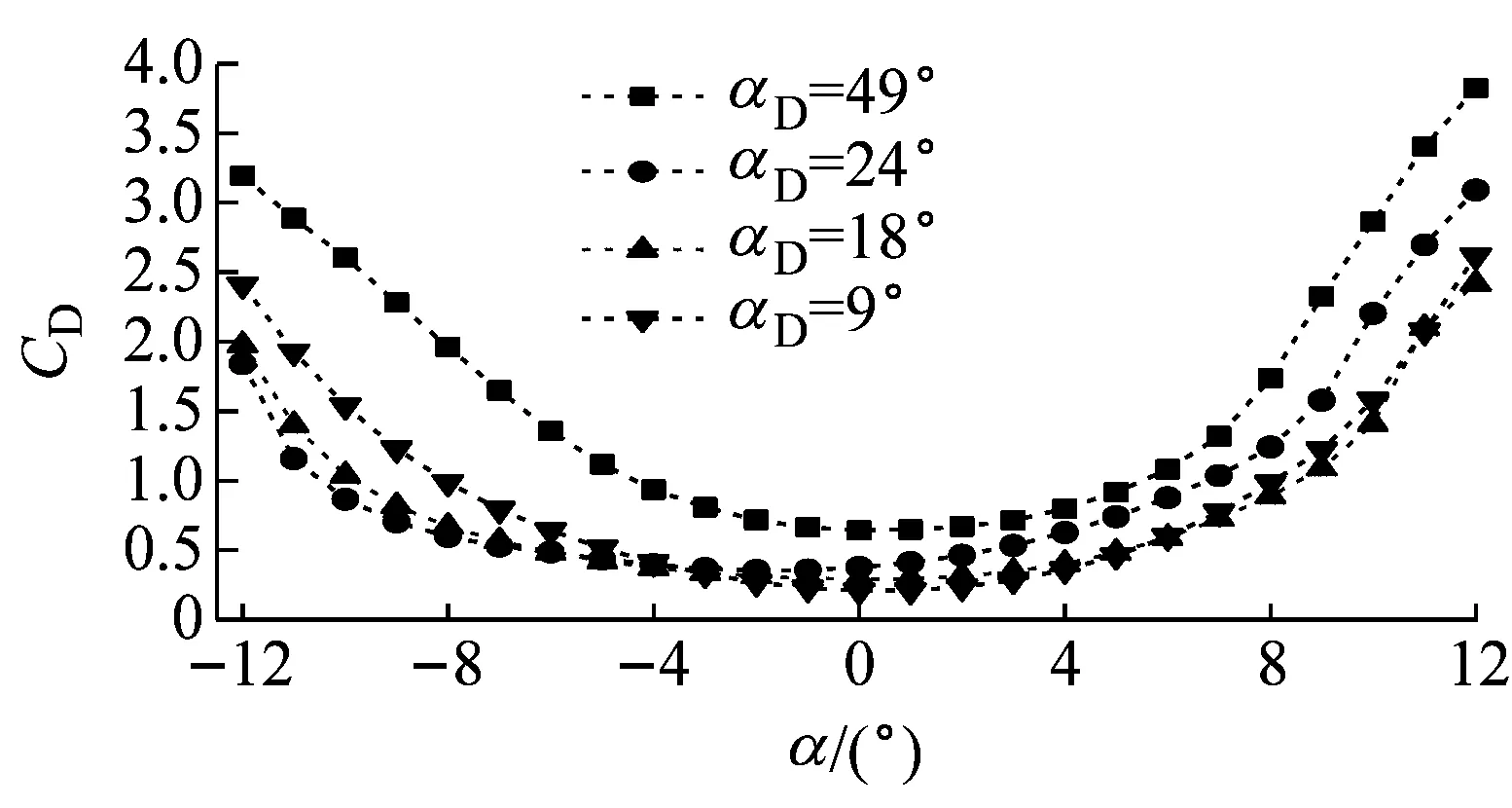
b
Fig.5 Drag coefficient versusαDand wind attack angle
随着αD的增大,CD增大,根据增速大小,可近似将计算断面分为3个区域: 区域1(αD=8°~18°);区域2 (αD=18°~24°);区域3(αD=24°~50°).在区域1及区域3,阻力系数随αD的变化相对平缓(图5a),而在区域2,阻力系数变化较大.
1.3.2升力系数
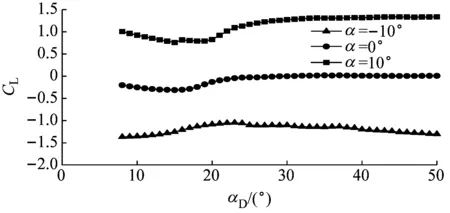
箱梁断面的升力系数随αD及风攻角变化如图6所示.对于不同的αD,升力系数随风攻角的变化趋势一致:升力系数随风攻角的增大而增大,且基本呈线性变化,在12°攻角下,CL≈1.5,在-12°攻角下,CL≈-1.5.当α=10°~12°时,升力系数趋于平缓,当αD>27°时,这一现象更为明显.
随着αD的增大,CL整体呈先减小后增大的趋势(图6a):当α≥0°时,这种趋势较为明显;而当α<0°时,αD对CL的影响则相对较小.根据这种变化趋势,可以将αD分为3个区域:区域1(αD=8°~16°);区域2(αD=16°~27°);区域3(αD=27°~50°).在区域1,CL整体随αD的增大而减小;在区域2,CL整体随αD的增大而增大;在区域3,CL随腹板的αD变化较为平缓.
a

b
Fig.6 Lift coefficient versusαDand wind attack angle
1.3.3扭矩系数
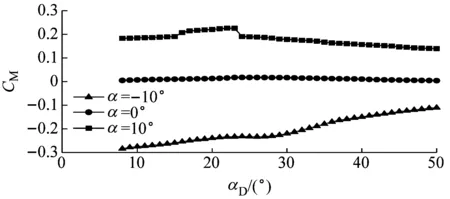
箱梁断面的扭矩系数随αD及风攻角变化如图7所示.在不同的αD下,扭矩系数随风攻角的变化趋势一致.CM在小攻角范围内(-5°~+5°)的扭矩系数基本呈线性变化:在α=-5°时,CM≈-0.12;在α=5°时,CM≈0.15.
CM在α=5°~12°时变化较为平缓,在0.10~0.20之间.而当α=-5°~-12°时,对于不同的αD,扭矩系数变化趋势发生了明显变化:当αD=41°~50°时,CM变化较为平缓,在0.10~0.15之间;当αD=8°~24°时,CM仍呈线性变化.
根据扭矩系数随风攻角的变化趋势,可近似将αD分为3个区域:区域1(αD=8°~24°);区域2(αD=24°~41°);区域3(αD=41°~50°).在区域1,CM在α=-12°~5°范围内呈线性变化,在α=5°~12°范围内变化平缓;在区域3,CM在α=-5°~5°范围内呈线性变化,在α=-5°~-12°及α=5°~12°两个范围内变化平缓;区域2中,CM随风攻角的变化趋势则介于区域3及区域1之间.
a

b
Fig.7 Torque coefficient versusαDand wind attack angle
1.3.4三分力系数结果讨论
本节从流场分析的角度,进一步解释在αD改变、不同风攻角下箱梁断面静三分力系数变化的原因.选取αD=15°及50°两个断面(分别记为断面1及断面2)进行对比分析.
1.3.4.1 阻力系数对比
图8为断面1、2在不同风攻角下的压力场及流迹线.从图8中可以看出:当风攻角较小时(α=±4°,0°),流动分离区域较小,分离区长度在B/3以内,高度小于D;而当风攻角较大时,分离区域已经扩展到整个桥宽区域,高度大于D,对于αD=50°的断面,在-12°风攻角下,甚至在底板及尾部下腹板位置均出现分离区.
分离区的迅速增大,是造成箱梁在大攻角下阻力系数迅速增大的主要原因.而当αD较小时,可有效减缓流动的分离,减小分离区,因此其阻力系数明显低于αD较大的箱梁断面.同时,较大的αD,也会造成前(后)缘较大的正(负)压分布区,从而进一步增大阻力系数.
1.3.4.2 升力系数对比
本文以0°风攻角下断面的压力分布图为例进行比较.如图8所示.对于下腹板,当αD较小时,在底板与下游腹板交接处存在负压力区,可以产生向下的升力分量.随着αD的增大,底板与下游腹板交接处漩涡脱落加强,位于该处的负压力区逐渐消失,升力系数也逐渐增大.在其他风攻角下的情况于此类似.
对比α=12°时断面1、2的压力分布可以发现:断面1的下表面腹板与底板交接处依然存在负压区;而断面2此时的下表面已经全部为正压,而上表面的负压分布也较大,从而造成升力系数增大.
1.3.4.3 扭矩系数对比
如图8所示,风攻角从-7°变化到-12°时,断面1下表面负压区增强,涡增大,而上表面始终维持正压状态,从而造成扭矩不断增大;而断面2的负压区及涡大小增长较小,且存在负压区后移的情况,从而其扭矩变化较为平缓.
风攻角从7°变化到12°时,断面1、2上表面负压区增强,涡增大,下表面正压增强,但由于前后缘压强同步增大或减小,从而抵消了由于压力变化造成的扭矩变化,因此扭矩变化较为平缓.

aαD=15°bαD=50°
图8 断面1及断面2在不同风攻角下的压力场及流迹线
Fig.8 Pressure field and flow trace of Section 1 and Section 2 at different wind attack angles
2 结构三维静风稳定计算
2.1 计算模型介绍
本文以一2×1 500 m斜拉桥为研究对象,在不考虑主梁结构外形改变对刚度影响的前提下,分析不同αD情况下的静风稳定.其中主梁三分力系数选用CFD方法计算结果,桥塔截面阻力系数取为1.4,斜拉索阻力系数按规范取为0.8.通过ANSYS自编程序,综合考虑结构几何及静风荷载非线性,采用平衡位置及逐级风速加载双重迭代方法[15],对不同αD下的静风稳定性进行计算.
桥梁跨径布置参见图9,跨径布置为244 m+408 m+1 500 m+1 500 m+408 m+244 m=4 304 m,主梁断面尺寸参见图1.基于上述桥梁结构,利用商业软件ANSYS建立三维有限元模型. 采用三维梁单元Beam188来模拟主梁、桥塔及桥墩单元,斜拉索采用Link10单元建模,并采用多段索单元来考虑斜拉索的垂度及几何非线性的影响,桥梁的结构参数列于表1,有限元模型如图10所示.

图9 桥梁结构总体立面布置图 (单位:m)

表1 桥梁主要结构参数表

a 总体划分
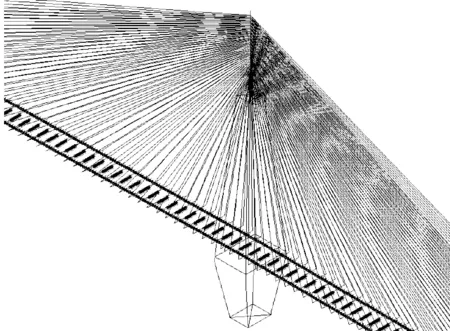
b 细部划分
2.2 静风稳定结果
图11为不同初始风攻角下,临界风速Ucr随αD的变化曲线.风攻角为+3°情况下的静风失稳临界风速要低于0°和-3°攻角下的临界风速.αD在9°~23°范围内的临界风速较高,这与第2节中关于扭矩系数在区域1(8°~24°)有较小的计算结果较为一致.
以0°初始风攻角为例,将不同αD断面跨中位置在70 m·s-1风速下的静风位移进行比较,分析结构静风失稳前的过程,如图12所示.随着断面形状的改变,扭转位移和竖向位移均有明显差别.通过改变αD,可以有效地减小0°初始风攻角下各风速点的竖向位移或扭转位移.在一定的αD范围内(9°~23°),竖向位移或扭转位移较小,这有利于提高静风失稳临界风速.

图11 不同αD下的静风失稳临界风速

图12 风速70 m·s-1下不同断面主梁跨中位移(0°风攻角)
Fig.12 Mid-span displacement of main girders at a wind speed of 70 m/s with different cross-sections (0° wind attack angle)
2.3 静风稳定结果讨论
通过比较不同αD下三分力系数及跨中位移(图13、图14),可以发现,在αD=20°附近,对应的CM值大于零,但此时在高风速下的扭转位移接近甚至小于零.通过对桥梁三维模型进一步分析,可以发现,除气动力矩外,由CD产生的气动阻力也可以使断面发生扭转变形.

图13 三分力系数随αD变化曲线(0°风攻角)
Fig.13 Aerodynamic coefficients versusαD(0° wind attack angle)

a αD=15°,Ucr=116.875 m·s-1

b αD=22°,Ucr=91.250 m·s-1

c αD=16°,Ucr=117.500 m·s-1

d αD=19°,Ucr=105.625 m·s-1
图14 结构风速-位移曲线
Fig.14 Structural displacement versus wind velocity
如图15所示,类似于摆锤的运动,竖向力与气动阻力的共同作用下,断面会产生逆时针转动.当αD<15°时,CM值较小, “摆锤”作用对于主梁的扭转变形占主导因素,主梁发生逆时针转动,但只会发生较小角度的转动,此时对应的负攻角范围内的CM值大于零,两个作用相互抵消,减小了主梁的扭转位移.同时,对应的CL值小于零,即对应的气动升力产生向下的竖向位移,使拉索应力增强,增加了结构的刚度.在上述因素的综合作用下,结构的扭转位移较小,如图14a所示.
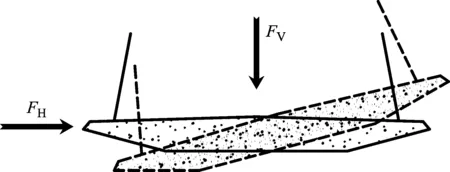
图15 阻力作用产生扭转变形示意图
当αD>27°时,CM值较大,对应的气动力矩项对于扭转变形一开始就占主导因素,产生顺时针转动,由此进一步增大结构所受的气动力矩,结构扭转变形增大,不利于结构的静风稳定.于此同时,当αD增大时,CL值也随之增大,对应的气动升力产生向上的竖向位移,使拉索索力减小甚至失效,削弱了结构的刚度.这些因素的综合作用,使扭转变形趋于发散,如图14b所示.
当15°<αD<27°时,对应断面的CL值、CM值随αD增大而增大.这类断面对应的结构位移风速曲线,甚至出现了扭转及竖向位曲线转折的现象,如图15c、15d所示.
3 典型断面静风失稳临界风速对比
为了对上述讨论结果进一步的验证,本节选取αD=15°(断面1)及αD=50°(断面2)的断面进行对比验证,进一步分析它们的差异.
两个断面静三分力系数对比如图16所示.两个断面的CM曲线在-4°~10°攻角范围内几乎完全重合.断面2在-4°攻角以下,CM曲线斜率开始减小,趋于零.两个断面的CL曲线形状基本相同.断面1的CL值比断面2小0.4左右.断面1的CD值小于断面2.
断面1和断面2在不同初始风攻角下的静风失稳临界风速如表2所示.断面1和断面2在不同初始风攻角下跨中的静风位移-风速曲线见图17.计算结果表明,通过改变αD,可以将静风失稳临界风速由83.75 m·s-1提高至103.75 m·s-1.即通过改变下腹板倾角能够比较明显地提高近流线型箱梁断面的静风稳定性能.选用倾角较小的断面,可以有效地增大下腹板的负压,从而有效地降低主梁的升力系数,同时降低阻力系数,进而达到提高静风稳定失稳风速的目的.
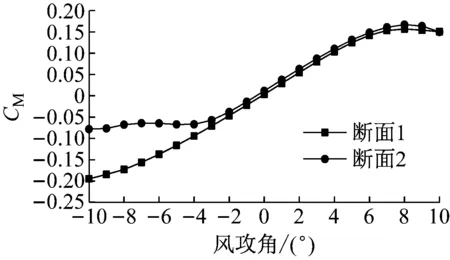
a CM值对比图
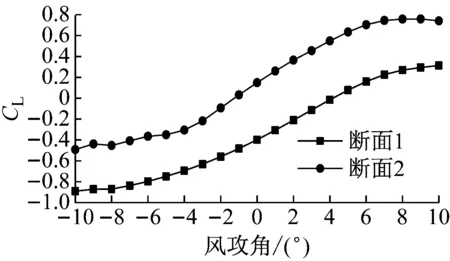
b CL值对比图

c CD值对比图
图16 两个断面的静三分力对比图
Fig.16 Comparison of aerodynamic coefficients between two sections


aα=0°
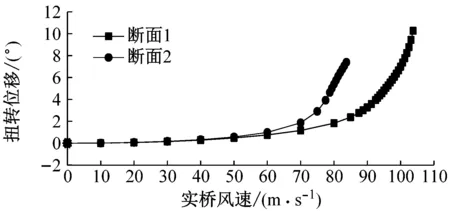
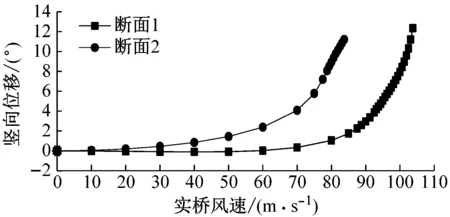
bα=3°


cα=-3°
图17 不同断面风速-位移曲线
Fig.17 Structural displacement versus wind velocity in different sections

表2 不同断面静风失稳临界风速
4 结论
(1) 分离区的迅速增大,是造成箱梁在较大风攻角下阻力系数迅速增大的主要原因.较小的αD有效地减缓了流动的分离,减小了分离区,因此其阻力系数明显低于αD较大的箱梁断面.而较大的αD也会造成前缘较大的正压分布区及尾部较大的负压分布区,进一步增大了阻力系数.
(2) 当αD较小时,在底板与下游腹板交接处存在负压力区,可以产生向下的升力分量.当αD逐渐增大时,底板与下游腹板交接处漩涡脱落加强,位于该处的负压力区逐渐消失,从而升力系数增大.
(3) 对于CM值较小的断面(αD<15°),气动阻力的“摆锤”作用对于扭转变形占主导因素,同时对应的CL值小于零,使拉索应力增强,增加了结构的刚度,结构的位移较小;对于CM值较大的断面(αD>27°),逐渐增大的风速及扭转变形对结构所受的气动力矩均产生不利影响,CL值也随之增大,使拉索应力减小甚至为零,削弱了结构的刚度.使扭转变形趋于发散.
(4) 当αD=9°~23°时,下腹板的负压增大,可以有效地降低主梁的升力系数,同时降低阻力系数,也可以有效地减小各风速点的竖向位移或扭转位移,从而达到提高静风稳定失稳风速的目的.
