模糊数学理论在地裂缝灾害危险性评估中的应用
2019-08-06文新征甄平福拜亚南罗晓峰
文新征 甄平福 彭 敏 拜亚南 罗晓峰
(1. 信息产业部电子综合勘察研究院, 陕西 西安 710054;2. 中交第一公路勘察设计研究院有限公司, 陕西 西安 710075;3. 内蒙古科技大学,内蒙古 包头 014010)
地裂缝是一种常见的区域性地质灾害,在世界各国都有发现,特别是在许多经济发达人口密集的大中型城市,其灾害频率及发展状况逐年加剧,其中西安地裂缝已成为典型代表。在大西北建设战略的背景下,加快西安城市发展步伐已成为迫切需要,然而地裂缝灾害却成为制约其发展的一个重要的“瓶颈”,因此开展地裂缝研究工作并对其灾害危险性进行分析评估显得尤为重要。
目前对地裂缝地质灾害危险性评估的方法多为定性的方法,即主要在调查和收集资料的基础上,通过分析成因、发展状况及危害程度,综合划分危险性分区,评价其对建设工程的影响作用。这种评估方法往往带有很大的主观性,忽略了评估系统各因素之间内在关系规律的揭示,对在建设工程中应用的理论和实践指导具有一定的局限性。因此,笔者以西安地裂缝为例尝试从研究区评估系统出发,提出地裂缝灾害危险性综合评价指标体系及分级标准,运用模糊数学理论[1-3],构建量化模型,分析研究各评价指标对评估分级标准的影响关系,收到了较为有效的评估效果。
1 构建地裂缝灾害评估指标体系及标准分级
根据研究区西安地裂缝构造特征和成因机制分析[4]及分布发展变化规律,参照相关已有研究资料[5-7],可以认识到,本质上西安地裂缝是先存地质构造(断裂系) 在现代引张应力场作用下蠕动而产生的断裂,表现为地面开裂、裂缝,这里的现代引张应力场作用主要是指地震活动、水文活动及人类工程活动等加剧断裂活动的作用。为了便于评估指标的选取和评估系统的建立,分别从基本因素、影响因素及灾害特征三大方面出发,综合筛选了8 个指标建立西安地裂缝灾害危险性评估指标体系及标准分级,详见表1。

表1 地裂缝灾害危险性评估指标体系及标准分级
2 模糊数学理论在地裂缝灾害危险性评估系统中的应用
2.1 模糊数学理论概述
模糊数学是从量上来研究分析和解决模糊问题的一个数学分支,它是以1965 年美国控制论专家L.A.Zadeh 教授最早提出的“模糊集合论”[8]为基础发展起来的数学理论。模糊数学的基本思想是以模糊系统为研究对象,通过“模糊集合”建造数学模型,逐步建立运算、变换规律,最终寻求解决模糊问题的有效数学方法。目前,模糊数学应用中的方法有模糊模式识别法、模糊聚类分析法、模糊综合评判法及模糊数值计算法等。
工程建设中的地质灾害问题常常错综复杂,蕴含着众多的模糊不确定性,例如:地质概念难以精确定义,划分界限模糊不清;地质系统本构关系复杂,难以识别;参数量测不够精确等。因此,从一定意义上说,模糊性已经成为解决工程地质问题的首要矛盾。在此,为了有效解决地裂缝灾害危险性评估的模糊性问题,笔者尝试运用模糊综合评判的方法进行相应的分析研究。
2.2 模糊综合评判的方法及应用
模糊综合评判就是运用模糊数学的方法对受多个因素制约的模糊系统(事物或对象) 进行总的评判。模糊综合评判的数学模型依据评判系统因素分类层次可分为一级模型和多级模型,本文对地裂缝灾害危害性评估包括一级模型模糊综合评判及二级模型模糊综合评判。
1) 一级模型模糊综合评判
①建立评判模糊集合,建立评判指标因素集U={u1,u2,u3,u4,u5,u6,u7,u8},其中u1~u8分别依次对应上表1中①~⑧各指标;建立评判集V={v1, v2, v3, v4},其中v1~v4分别依次对应上表1 中Ⅰ~Ⅳ各评价标准分级;
②确定各评价因素的隶属度, 评价因素隶属度的确定方法:对于定性指标因素(如表1 中②、④、⑥、⑧),主要采用专家经验评定法,直接给出隶属度取值,见表2;对于定量指标因素(如表1 中①、③、⑤、⑦),常用隶属函数代入实测值确定。隶属函数的常见分布形式有矩型、梯型、抛物线型、正态分布、哥西分布及岭型分布等,具体应用中根据研究对象分布特征选定。在地裂缝灾害评估系统中,综合各因素分布特征,选取“梯型分布”为隶属度函数,其分布函数图形见图1。

表2 定性指标隶属度取值表

图1 “梯型”隶属度函数分布图
图1 中,A (x) 表示定量指标因素分别对应评价分级的隶属度函数,x 为因素实测值;a、b、c 分别为各因素分级标准取值,a′、b′、c′为其相应的模糊性修正值,且a<a′<b<b′<c′<c。其具体表达公式如下:

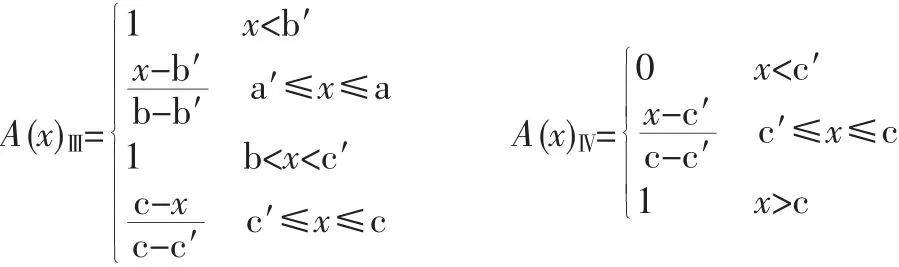
③确定单因素评判模糊矩阵,根据从U 到V 的隶属度可得模糊矩阵R,即建立评判指标因素集到评判集的一个模糊映射关系。
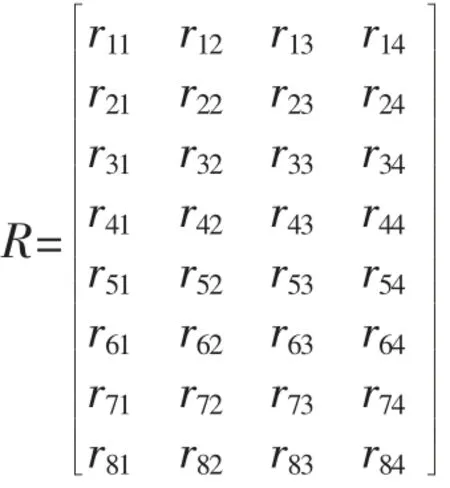
可见,由(U,V,R) 就共同构成了一个评估系统模型。
④确定各评价因素的权重,在评判系统中,各评价因素对评价分级的影响作用及重要性各不相同,因此综合评价时应赋予一定的权重值。可根据已有研究成果或结合专家经验先估计出一组权重值,然后通过大量的试运算,比较分析运算得到的综合评判结果与实际情况的拟合性,直到两者基本一致为止。由此可得U 上的一个权重系数模糊子集A:


其中“·”表示模糊子集的合成运算,运算法则同普通实数矩阵的乘法运算过程相同,只需将实数加法中的“+”改为集合取大运算的“∨”,将实数乘法中的“·”改为集合取小运算的“∧”。即

2) 二级模型模糊综合评判
二级模型可以进一步弥补一级模型的综合评判的不足之处,主要表现为:当评价因子过多时,其权重取值就会偏小,往往导致评价结果差异性也会变小;另外,当评价因子过多时,会使对各因子的权重分配的合理性变得更加困难。根据表1 对评价指标的两级分类情况,八个参数指标又可以划分为三大类,依此进行二级模糊综合评判的方法步骤如下:
①将因素集U 分为三个子集U1、U2、U3(分别对应表1中基本因素、影响因素、灾害特征),且满足U1∪U2∪U3=U,且两两取交集为空集。U1={a1, a2, a3} , U2={a4, a5, a6} , U3={a7, a8}。
②对每个子集Ui 分别按一级模型进行综合评判:

其中,A*i为Ui上的权重分配,且满足Σa*i=1。
③将每个子集Ui 进行单因素评判,可得二次模型评判矩阵:


2.3 评定结果分析
3 结语
1) 通过对模糊数学理论在西安地裂缝灾害危险性评估中的应用分析表明:以“模糊集”和“隶属度”为基础的模糊综合评判模型,运用数学量化手段解决地质灾害评估系统的模糊性问题,清晰明了,简单可行,对于同类工程地质问题具有参考价值及指导意义;2) 在模糊综合评判建模过程中,依然存在着不足之处。其一,评价系统中定性指标隶属度的取值主要依据专家经验评定的方法确定,具有一定的主观色彩;其二,各评价因子权重分配采用先是估值再进行实效拟合性试算的方法,当系统复杂参数较多时,运算工作量将加大;其三,在采用多级综合评价模型时,评价系统中参与因子越多,多层次分级分类越困难,同时也增加了评价因子隶属度及权重分配的难度等。
