煤矿巷道层状围岩松动圈范围的发育规律

胡世敬，裴 钻

（1.贵州交通职业技术学院，贵州 贵阳 550008；2.成都理工大学 地质灾害防治与地质环境保护国家重点实验室，四川 成都 610059）

巷道开挖后，岩体中原始应力状态进行调整，重新分布，巷道附近的应力由三向应力状态转变成二向应力状态，径向力近乎为0，应力大于岩体强度时致使围岩变形破坏，直至应力小于或等于岩体强度破坏停止，通常形成不规则的环形范围称为围岩松动圈[1-4]。围岩松动圈是构造应力、围岩属性及结构特征共同作用的综合性结果，随着时间以及应力不断的演化改变，宏观呈现由表及里，由局部到整体的特征[5-6]。目前关于松动范围确定主要分为物理检测和理论解析计算（包括数值分析和物理模型），从不同角度确定了围岩松动圈范围及发育规律[7-9]。其中物理检测最直观，直接反映围岩特征，常用方法包括超声波、地质雷达、地震波、渗透率测试、电阻率测试、钻孔窥视等。理论解析计算主要有弹塑性应力解析、Hoek-Brown强度折减法、双剪切理论、无量纲理论以及有限元数值分析、物理模型理论推导等[10-13]。然而，理论研究有较多的限制与假设，通常与实际地质情况有误差。目前，声波监测围岩松动圈范围广泛应用于实际工程并取得较好的效果[14]。以贵州织金煤矿巷道为研究实例，采用声波测试方法确定松动范围，重点分析研究巷道轴线与岩层走向在不同夹角情况下的围岩松动圈的发育范围和规律。

1 工程概况及声波测试

1.1 煤矿巷道地质概况

贵州织金煤矿位于扬子江台地，属于云贵高原。煤矿位于织金背斜北西一翼，巷道位于地下200～300 m，围岩岩体为三叠系法郎组中-下统层状粉质砂岩，岩层为单斜构造，岩层倾角为27°～32°。围岩节理较发育，围岩密度为2.7 g/cm3，体积模量为1.22 GPa，剪切模量为 0.72 GPa，内摩擦角为 33°，黏聚力为 3.2 MPa，抗拉强度为 1.34 MPa。

1.2 声波测试原理及方法

根据弹塑性介质中的波动理论，一般应力波波速公式为：

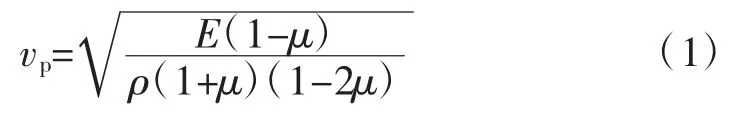
式中：vp为围岩声波速度；ρ为围岩密度；E为围岩弹性模量；μ为围岩泊松比。

声波测试原理为采用声波在不同裂隙岩体介质中传播速度衰减特征，判断介质属性差异。对于同一岩体介质而言，完整性高则声波速度快；完整性低，则声波速度慢。对于获取的“深度-声波速度”曲线，在速度的突变处，通常可以判定为松动圈范围边界[14-15]。深度-声波速度关系图如图1。

图1 深度-声波速度关系图

此次声波仪器采用的是RSM-SY5型声波仪，由武汉中岩科技公司所生产，单孔测试采用一发双收，由内而外沿孔壁连续观测，移动步距为20 cm。声波测试示意图如图2。

图2 声波测试示意图

计算声波速度v所使用的计算公式为：

式中：t1、t2为声波从发射探头到相应接受探头的历时；L1、L2为发射探头到相应接受探头的距离。

1.3 声波测试方案

矿区巷道根据不同生产作业功能，分为2种断面形式。直墙拱形巷道，宽度 B 为 3.5～4.5 m，平均为 4.0 m，拱高 h1为 1.0～1.5 m，平均为 1.2 m，h2为1.8～2.5 m，平均为 2.1 m；圆拱形巷道，宽度 B 为3.5～4.0 m，平均为 3.8 m，高度 H 为 3.0～3.5 m，平均为3.2 m。声波测试钻孔以环形布置，共设8个测试部位并予以编号（1#～8#），直墙拱形和圆拱形断面测试布置如图3和图4。

图3 直墙拱形断面测试布置图

图4 圆拱形断面测试布置图

测试断面分为4种类型：巷道轴向与岩层走向的夹角 α 为 0°（近似平行状态）、30°±5°、60°±5°以及90°（近似垂直状态），每种类型的断面测试4～6组。2种断面形式共测试不少于32组，以避免离散型统计。孔深设计必须满足声波速度近似原岩波动速度，明确判定为非松动破裂区。

2 围岩松动圈发育规律

2.1 松动圈范围判定

围岩松动圈根据现场测试孔获取的声波速度以及测试孔的深度，绘制“深度-声波速度”图。一般由巷道墙壁及里，声波速度会逐渐增加，但存在反复现象，声波出现突变，并且维持与原岩速度一定范围内，则为松动范围的边界。选择某个巷道走向与岩层走向近似平行的直墙拱形断面的测试孔（1#、2#、3#、4#、6#）为例，直墙断面声波测试实例图如图5。从图5中可得，该断面的原岩声波平均速度约为3 210 m/s，测试孔初始段声波速度为1 650～1 870 m/s，平均约为1 750 m/s，但声波突变对应的测试孔深度l存在较大差异，分别取值为：l1=2.74 m，l2=4.34 m，l3=2.24 m，l4=2.59 m，l6=1.92 m。

图5 直墙断面声波测试实例图

2.2 松动圈范围测试成果

根据上述声波测试围岩松动圈的范围的判定方法，共计测试40组，成果统计见表1。依据测试松动圈的长度l，绘制的巷道轴向与岩层走向不同夹角α情况下直墙拱形断面和圆拱形断面围岩松动圈范围发育规律如图6～图7。

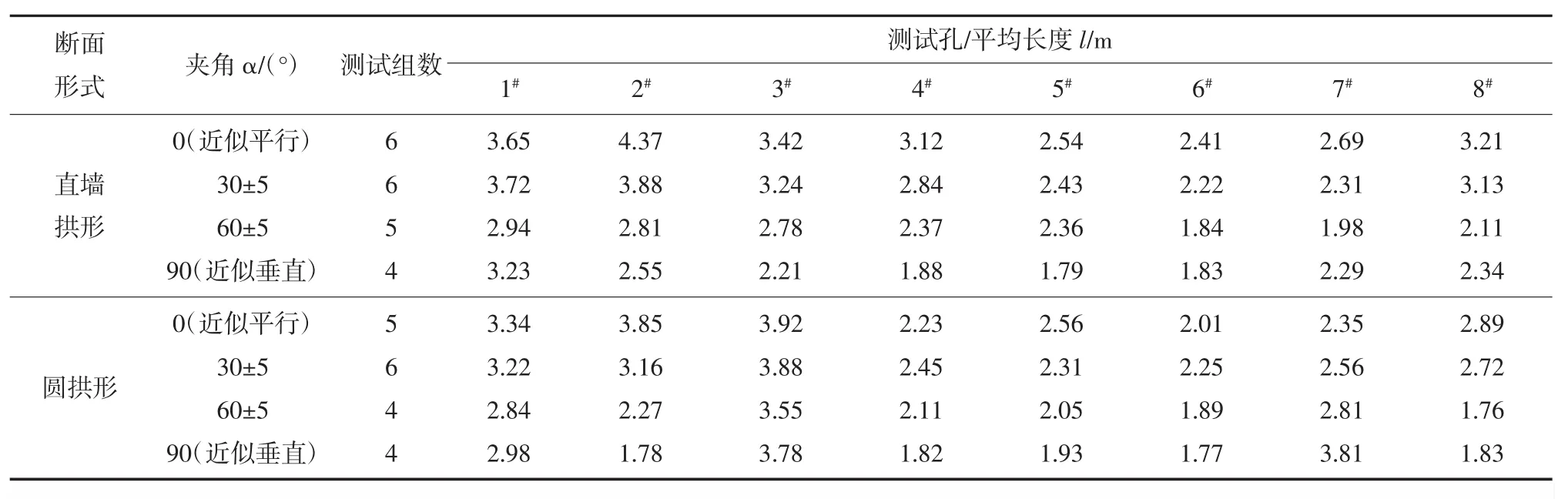
表1 松动圈测试成果表

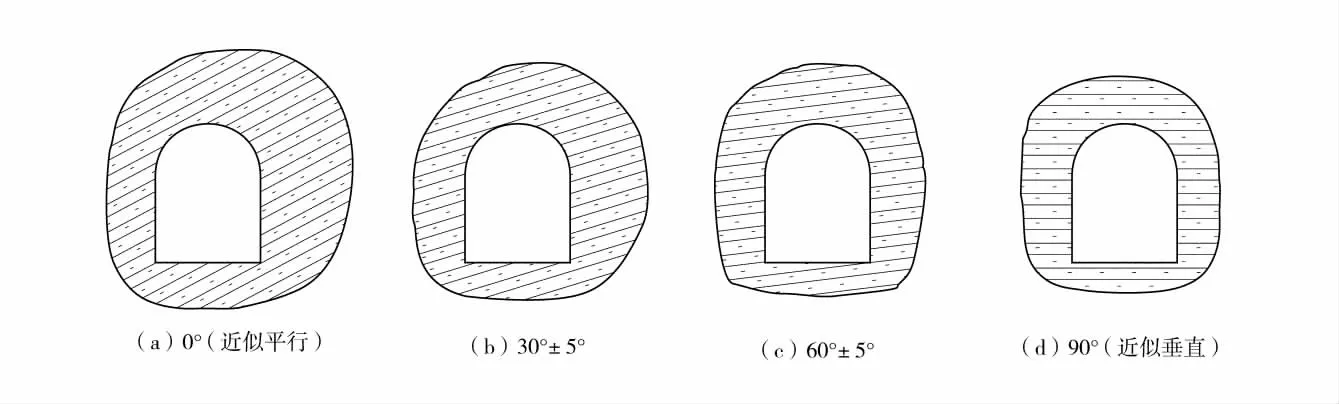
图6 直墙拱形断面层状围岩巷道松动圈范围发育规律图

2.3 直墙拱形断面松动圈发育规律

直墙拱形断面巷道轴向与岩层走向夹角α由0°到90°范围内变化，围岩松动圈发育规律主要表现以下几点：①当夹角为0°（近似平行）时，围岩松动圈最大部位为顺倾侧壁拱脚，其次为拱顶以及侧壁部位，最大松动长度近似等于巷道宽度B，反倾侧壁则松动范围较小，约为巷道宽度的B/3～B/2；②随着夹角α逐渐增大，顺倾侧壁拱脚松动范围逐渐减小，而其它部分松动范围逐渐增大，直至夹角90°（近似垂直）时，巷道拱顶以及两侧松动圈范围基本一致，约为（B/2±0.4）m；③当夹角为 0°（近似平行）时巷道底板松动区范围最大，约为B/2；当夹角α逐步增大后，松动范围变化不大，通常为（B/3±0.3）m；顺倾直墙脚部位的松动范围随着夹角α的变大逐渐呈现由大变小，反倾直墙脚部松动范围则相反。

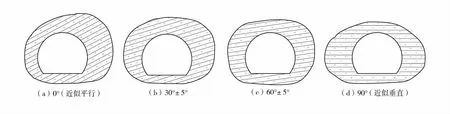
图7 圆拱形断面层状围岩巷道松动圈范围发育规律图

2.4 圆拱形断面松动圈发育规律

圆拱形断面巷道轴向与岩层走向夹角α由0°到90°范围内变化，围岩松动圈发育规律主要表现以下几点：①当夹角为0°（近似平行）时，围岩松动圈最大部位为顺倾侧壁中上部，其次为拱顶以及侧壁拱脚，最大松动长度近似等于巷道宽度2B/3～B，反倾侧壁松动范围则较小，约为巷道宽度的B/4～B/3；②随着夹角α逐渐增大，顺倾侧壁范围逐步减小，而反倾侧壁逐渐增大，直至夹角为90°（近似垂直）时，两侧壁松动范围近似一致，约为3B/4～B；③随着夹角α的逐渐增大，拱顶松动范围逐渐减小，约为B/3～2B/3，拱脚松动范围变化不大，通常为B/4～B/3范围内。

3 巷道围岩设计及支护建议

当夹角α=0°，或小角度近似平行时，顺层侧壁至拱顶部位松弛范围最大，尤其是拱上侧角最大可达巷道宽度B，甚至更长；随着夹角α=0°逐步增大，松动范围逐渐不出现两侧壁近似一致，拱顶松动范围逐步降低，巷道底板松动范围变化不大；随着夹角α的逐步增大，直墙拱形断面巷道的松动范围近似垂直方向较长，水平方向较短的不规则椭圆形状，而圆拱形断面巷道则形成水平方向较长，垂直方向较短的不规则椭圆形状。

因此，巷道设计时需要根据地质情况，尤其是考虑岩层空间分布，在满足生产条件的前提下，巷道轴向线尽量与岩层走向垂直，或大角度相交，则松动区范围相对较小。图6和图7的松动区范围分布情况可作为巷道支护的参考依据。

4 结论

1）通过声波测试方法，确定织金煤矿层状巷道松动岩体的声波平均速度为1 750 m/s，原岩声波平均速度为3 210 m/s，巷道开挖后岩体质量下降明显。以巷道走向与岩层夹角α的大小（0°（近似平行）、30°±5°、60°±5°以及 90°（近似垂直）） 为分类依据，将直墙拱形断面和圆拱形断面分别进行多样本测试，获取松动圈发育规律。

2）当夹角α为0°（近似平行）时，巷道松动范围呈非对称性，顺倾侧壁（2#测试孔）最大松动长度约为巷道宽度B；夹角α由小变大的过程，顺倾侧壁以及拱顶的松动范围逐渐减小，而反倾侧壁松动圈范围逐渐增大，直至近似一致；拱顶松动范围随着夹角α的变大逐步变小，而巷道底板松动范围变化不大。

3）以测试结果为依据，绘制了层状围岩松动圈的发育规律，为巷道的设计以及支护提供了可靠依据。