基于Abaqus的不对中激励力作用下轴系振动特性研究

楼京俊 王建午 刘丽滨 杨庆超

（1.海军工程大学船舶与海洋学院 武汉 430033）（2.海军装备部驻上海地区第二军事代表室 上海 200120）

1 引言

轴系对中不良时，在弹性联轴器和轴系各连接法兰处会产生强烈的不对中激励，这将改变轴系原有的振动传递和响应特性，从而导致轴系异常振动［1～4］。目前，关于轴系校中不良与轴系振动特性之间相互影响规律的研究较多，付波、王延溥、徐俊辉等从轴系不对中时的振动特性、振动诊断与处理方法等角度对轴系不对中与轴系振动之间的相互关系进行了研究［5～7］；李方、周奇郑等推导了不对中状态下的轴系振动响应计算公式，并分析了不对中量对其振动响应曲线的影响［8～9］；杨俊等分析了三种不对中情况下弹性联轴器的受力状态，通过对不对中激励力进行数值仿真和台架试验研究了轴系不对中量对轴系振动的影响［10］；蒋义海、吴振宇等以转子不对中故障平台为例，基于计算机软件建立了轴系仿真模型，计算并分析了不对中故障下轴系的振动响应特性［11～12］。

为进一步弄清轴系不对中激励力作用下的轴系振动特性，掌握轴系校中对其振动特性的影响，本文将对激励力作用下的轴系有限转子动力学方程进行推导，同时根据实船轴系在Abaqus软件中建立其有限元仿真模型，并对模型开展模态分析与瞬态动力学分析，由此得出不对中激励与轴系振动特性之间的相互影响关系。

2 轴系有限转子动力学方程

轴系实质上是一个质量连续分布的转子系统，用有限元法可将其离散化为许多具有若干集总质量的多自由度转子单元，这些转子单元按位置与受力状态可进一步分为两大类：梁单元与轴承支承处的的转子单元。

1）梁单元动力学方程

梁单元模型如图1所示，每一个梁单元都由两个节点组成，每一节点有沿水平方向位移x、沿竖直方向位移y、绕水平轴旋转角度θx与绕竖直轴旋转角度θy四个空间自由度。该梁单元的空间位移向量可表示为

式中，i、i+1为节点编号。

图1 轴系梁单元模型图

由拉格朗日法可推导出该梁单元动力学方程：

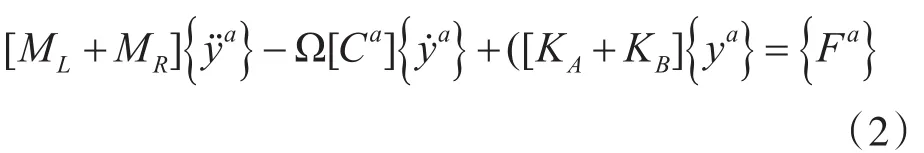
式中，ML、MR分别为梁单元位移质量矩阵与转角质量矩阵，Ca为梁单元阻尼矩阵，KA、KB分别为梁单元弯曲刚度与轴向刚度矩阵，Fa为梁单元上作用的不平衡力、外载荷等。

2）轴承支承处转子动力学方程

与梁单元动力学方程类似，线性轴承支承处转子单元动力学方程为

式中，yb、Cb、Kb、Fb分别为各轴承支承处转子单元的位移向量、阻尼矩阵、刚度矩阵及外载荷。

综合各轴系转子单元并将它们的质量、刚度、阻尼、受力进行等效合并，可得到整个轴系动力学方程：

上式中，F含轴系各零部件重力、外载荷、轴系不平衡力及不对中造成的激励力。

3 轴系有限元模型的建立

某船舶推进轴系结构简图如图2，该轴系由艉至艏依次为螺旋桨、艉轴、艉后轴承、艉中轴承、艉前轴承、推力轴、推力轴承、弹性联轴器、经航电机、中间轴、中间轴承、轮胎离合器。

图2 某船舶推进轴系结构简图

表1 轴系基本参数表

对上述推进轴系进行合理简化并在Abaqus中建立其仿真模型，用到的轴系基本参数如表1；建模时采用三维可变形梁来模拟轴系，用Springs单元来模拟各支承轴承，螺旋桨用实体七叶桨进行模拟，轴系各零部件用点质量进行模拟并施加于对应位置；由于轴系艏端以轮胎离合器与主推进装置相连，在建模时将其作简支处理；在各质量集中单元处对轴系进行分段处理，并在分割节点处设置点质量/惯性值用以赋予各部件质量属性；另外，在各轴承支承处创建参考点，用于模拟轴承基座并固定轴系。

在几何模型中首先根据轴系基本参数表设置其材料、截面属性及各零部件点质量，然后设置各轴承线性弹簧/阻尼连接器刚度。在连接器刚度设置时应注意计入各轴承工作长度对支撑弹簧数量的影响，此处用3个等间隔垂向和水平弹簧模拟艉后轴承，用2个等间隔垂向和水平弹簧模拟艉中、艉前轴承，用1个垂向和水平弹簧模拟中间轴承；推力轴承在设置时不但要计入水平、竖直方向的刚度，还需计入纵向刚度的影响，故用1个水平、1个垂向和1个纵向弹簧进行模拟。此外，由于艉后轴承离螺旋桨较近，受螺旋桨“悬臂作用”影响明显，一般具有较大轴承负载，因此在赋值时常将其垂向油膜刚度设置得比水平方向油膜刚度稍大，而使其他各轴承垂向刚度与水平刚度保持一致。各轴承刚度设定值见同表1。

根据实际情况，在各轴承支座模拟结点上施加固支边界条件，同时在螺旋桨中心处设置一参考点，并将该参考点与轴系相应结点建立coupling约束。最后对设定好的轴系几何模型进行网格划分与单元类型设置，得到其有限元模型如图3，其中轴段上共生成了223个结点和212个单元。

图3 轴系有限元模型示意图

4 不对中激励作用下轴系振动特性分析

4.1 轴系模态分析

各激振力在传递过程中首先要经过轴系，轴系的固有特性会对各激振力产生不同程度的放大或减弱效果，因而对轴系开展模态分析以弄清轴系本身固有特性是研究不同激励力作用下轴系振动特性的前提。

在模型中建立频率分析步，采用Lanczos法对轴系模态振型和频率进行求解。计算得到轴系一、二、三阶纵振振型如图4所示，其对应模态频率分别为 40.30Hz、90.34Hz、180.05Hz，由图可知，轴系一阶纵振振型最大变形处主要集中在艉轴中部，二阶纵振主要集中在在中间轴附近，三阶纵振主要集中在艉轴艏端。

图4 轴系纵振振型图

轴系前4阶横振振型如图5所示，对应模态频率分别为 8.69Hz、12.51Hz、18.29Hz、20Hz，一阶横振变形主要发生在艉轴靠近螺旋桨一端，二阶横振主要发生在在中间轴承附近，三、四阶横振主要发生在艉轴和中间轴上，各横振节点基本位于轴承支承处。

4.2 不对中激励作用下轴系振动响应分析

从模态分析得到的各阶振型图可以看出，不同频率激励力作用下，轴系各连接法兰和弹性联轴器处均会发生较大变形，这将改变轴系的校中状态和工作性能。轴系联轴器不对中是指其两端转子中心存在一定的位移或角度偏差，主要分为三种型式：平行不对中、角度不对中和综合不对中，不对中联轴器对轴系振动产生的激励作用主要体现在其两侧节点会产生额外不对中激励力矩，该激励力矩最终以反作用力的形式作用在轴系上并引发轴系振动；这种不对中激励复杂且难以定量计算，它会随着轴系运转工况、联轴器在轴系中的位置以及不对中量的不同而发生改变。

图5 轴系横振振型图

由文献8中相关理论可知，轴系不对中产生的激励力为周期力，其主要谐波分量为轴系工作频率的1倍频与2倍频。在Abaqus中进行仿真时，需要先根据模态分析得到各轴系固有频率fi并按公式：ni=60fi求解出轴系临界转速ni，以避免设定的工作转速与临界转速相重合而引起共振；因此，在模型中把轴系工作转速设定为15r/s，同时将轴系不对中激励力分解为x、y两个方向上的谐波分量有：Fy=A1coswt+A2cos2wt和 Fx=A1sinwt+A2sin2wt。按照上述谐波分量表达式将单位不对中激励施加在联轴器相应节点位置，并对轴系进行瞬态动力学分析，以艉轴中间点为响应考察点，计算得到轴系振动响应曲线如图6，其中，图6（a）、6（c）、6（e）为考察点三个方向振动响应时域图，对它们分别进行傅里叶变换得到考察点振动响应频谱图如图6（b）、6（d）、6（f）。

由图6（a）、6（c）、6（e）可知，不对中激励力作用下轴系竖直、水平方向上的振动响应幅值比纵向振动大了约两个数量级，这表明联轴器不对中激励在轴系上的传递途径主要沿各轴承水平方向与竖直方向，只有小部分以纵向传递的方式由各轴承基座传递给船体；从图6（b）可以看出，不对中激励力作用下轴系纵向振动响应峰值主要出现在26Hz、30Hz、32Hz、40Hz、42Hz、103Hz、131Hz及180Hz等处，结合模态分析结果可以发现：26Hz、32Hz、42Hz、131Hz为轴系横振固有频率，40Hz、180Hz为轴系纵振固有频率，103Hz为螺旋桨模态频率，又因为轴系转频为15r/s，纵振响应曲线在30Hz出现了最高峰值，这表明轴系不对中激励在沿纵向传递时，传递形式主要为其2倍转频分量；与图6（b）分析过程类似，发现在图6（d）、6（f）中，不对中激励力作用下轴系竖直、水平方向的振动响应峰值除了出现在各结构固有频率处，在15Hz、30Hz也分别出现了较强烈的响应峰值，其中30Hz处还出现了最高峰值，由此可见，轴系不对中激励在沿竖直、水平方向传递时，传递形式为其1倍转频分量与2倍转频分量且以2倍转频为主要频谱。综上所述，不对中激励下轴系频率响应峰值主要在1倍转频与2倍转频处，分别为15Hz、30Hz，仿真结果与理论值基本一致。

5 结语

利用有限单元法将轴系离散成了多个具有集总质量的转子单元，同时推导出了各转子单元及整个系统的动力学方程；在此基础上以某实船轴系为例，在Abaqus中搭建了轴系有限元仿真模型，通过对模型开展模态和瞬态动力学分析，得到了轴系各阶模态振型、固有频率及不对中激励力作用下的轴系振动响应曲线，通过对比研究发现不对中激励作用下轴系的振动响应频谱主要表现为1倍转频与2倍转频的特征，其中2倍转频为主要分量且能通过纵振、横振相结合的方式进行传递，1倍转频则主要通过轴系横振的方式进行传递，这与理论分析基本相符，验证了该仿真模型的正确有效性。

图6 不对中激励力作用下轴系振动响应