多组群教学优化算法-神经网络-支持向量机组合模型在径流预测中的应用

崔东文

(云南省文山州水务局,云南 文山 663000)

由于河川径流预测的复杂性、非线性、随机性和不确定性,传统回归分析、数理统计等方法往往难以达到理想的预测效果。广义回归神经网络(generalized regression neural network, GRNN)、径向基神经网络(radial basis function, RBF)和支持向量机(support vector machines, SVM)因所具有的高容错性、智能化和自学习等能力已在水文预测预报中得到广泛应用[1-6]。然而,在径流预测预报中,GRNN、RBF、SVM模型存在两方面不足:①单一预测模型存在一定的局限性,如GRNN存在因训练样本过度训练而导致检验样本预测精度下降等不足; RBF存在因训练样本训练不充分而导致泛化能力降低等问题;SVM存在惩罚因子、核函数参数等难以确定的缺点。②难以合理选取GRNN、RBF、SVM模型参数,如GRNN的光滑因子、RBF的均方误差、径向基函数扩展速度、SVM的惩罚因子、核函数参数等。实例研究表明,模型参数的合理选取是提高GRNN、RBF、SVM模型预测精度的关键因素。目前GRNN、RBF、SVM模型参数的选取普遍采用人工试错的方法进行调试确定,极大地制约了GRNN、RBF、SVM在水文预测预报中的应用。为提高水文预测预报精度,组合预测模型[7-8]被提出。组合模型的构成单元主要有回归模型单元[9]、神经网络模型单元[7]、混合组合模型单元[10]等;组合模型的组合方法主要有加权平均法[8,11]、线性组合法[12]等。

表1 基准函数

近年来,基于模仿生物机制或自然现象的随机优化技术越来越受到各行业领域的重视,各种基于某一生物社会群体行为或自然物理现象的随机优化算法被一一提出,如多元优化算法[2]、果蝇优化算法[13]、蚁群优化算法[14]、人工鱼群算法[15]、粒子群优化算法[6]、灰狼优化算法[16]、花授粉算法[16]等,并成功用于优化GRNN、RBF、SVM模型相关参数。

为进一步提高年径流量预测精度,本文通过5个标准测试函数对多组群教学优化(multi-group teaching-learning optimization, MGTLO)算法进行仿真验证,提出基于MGTLO算法与GRNN、RBF、SVM模型单元融合的MGTLO-GRNN-RBF、MGTLO-GRNN-SVM、MGTLO-RBF-SVM、MGTLO-GRNN-RBF-SVM组合预测模型,以新疆伊犁河雅马渡水文站和云南省某水文站年径流量预测为例进行实例研究。

1 多组群教学优化算法及其验证

1.1 多组群教学优化算法

教学优化(TLBO)算法是Rao等[17]于2012年提出的新型全局优化算法,该算法分为教师阶段和学生阶段,教师阶段通过教师传授学生知识来提高班级学习成绩;学生阶段通过学生之间互相学习提高班级创造性,通过这两个阶段不断提高学生成绩来获得问题最优解。TLBO算法调节参数少,算法简单,但存在收敛速度慢,寻优精度低等不足[18]。多组群教学优化(MGTLO)算法是Kommadath等[19]提出的一种基于多组群改进的教学优化算法,该算法利用分组策略定义学生(种群)数量、组数和每组学生数量,通过选择每组学生中适应度值最好的学生作为该组教师并对各组教师适应度值进行比较,最终确定所有组学生中适应度值最好的学生作为教师,即待优化问题最优解,该算法的具体实现步骤参见文献[19]。

1.2 算法验证

为验证MGTLO算法寻优能力,选取5个标准测试函数(表1)对其进行仿真验证,求测试函数的极值,并将其结果与基本TLBO算法以及混合蛙跳算法(shuffled frog leaping algorithm, SFLA)、差分进化(differential evolution, DE)算法、粒子群优化(particle swarm optimization，PSO)算法的仿真结果进行对比。

5种算法参数设置如下:MGTLO算法最大迭代次数T=1 000,学生规模(种群)N=50,组数G=5;TLBO算法T=1 000,N=100;SLFA算法T=1 000,N=50,子群数K=5,子群内青蛙个数Np=10,子群数局部进化次数T1=10;DE算法T=1 000,N=50,上下限的尺度因子分别为0.8、0.2,交叉率CR=0.2;PSO算法T=1 000,N=50,惯性因子κ=0.729,局部学习因子、全局学习因子c1=c2=2.0,个体速度限制为[-0.1,0.1]。

采取5种算法均对测试函数寻优20次,利用20次寻优结果的平均值、标准差及平均单次运行时间(表2)对各种算法的优化性能进行评估。其中,平均值用于反映算法的寻优精度;标准差用于反映算法的稳定性;平均运行时间用于反映算法的寻优时效性。

表2 函数优化对比结果

从表2可以得出:①从单峰函数Quartic和Rosenbrock的寻优效果来看,MGTLO算法的寻优平均值、标准差均优于其他4种算法,表明MGTLO算法具有较好的寻优精度和稳定性能。从多峰函数Griewank的寻优效果来看,MGTLO算法、TLBO算法的寻优平均值、标准差均为0,寻优精度和稳定性优于SLFA、DE和PSO算法;对于Rastrigin和Ackley函数,MGTLO算法寻优精度和稳定性优于其他4种算法。以上表明MGTLO算法具有较好的跳出局部极值能力、全局极值寻优能力。②从平均运行时间来看,MGTLO算法对5个函数的平均运行时间在0.322～0.978 s之间,平均不到其他4种算法平均运行时间的1/5,表现出较好的寻优时效性。由此可见,对于单峰或多峰函数,MGTLO算法无论是从算法的寻优精度和稳定性能上看,还是算法的寻优时效性和跳出局部极值的能力而言,其寻优效果均优于其他4种算法。

2 组合预测模型

2.1 单一模型

2.1.1广义回归神经网络

(1)

式中:Xi、Yi为两个随机变量的样本观测值;n为样本容量;σ为高斯函数的宽度系数,即光滑因子。

2.1.2径向基神经网络

RBF是前向神经网络,由输入层、隐含层和输出层组成,其数学模型为[22]

(2)

式中:y为输出值;x为RBF输入向量;φi为RBF隐含层和输出层之间的权值;ci为RBF中心节点向量;γ为中心节点宽度。

研究表明,径向基函数扩展速度s对RBF预测精度有着关键性影响,s越大,函数拟合越平滑,但过大的s意味着需要更多的神经元以适应函数的快速变化;s过小,则会导致网络拟合效果不理想。均方误差e设置过小,会导致网络过拟合而降低其泛化能力;e设置过大则会导致网络欠拟合而得不到理想的预测效果。设置合理的神经元最大数目M和两次显示之间所添加神经元数目F可有效平衡RBF的收敛速度和预测精度。本文基于Matlab神经网络工具箱,利用MGTLO算法搜寻Matlab神经网络工具箱中newrb()函数的最佳参数e、s、M、F。

2.1.3支持向量机

SVM是通过核函数将低维空间中非线性回归问题映射到高维特征空间,然后在高维特征空间中求解凸优化问题。设含有l个训练样本的集合为{(xi,yi),i=1,2,…,l},xi∈RD为第i个训练样本输入列向量,yi∈R为第i个样本输出变量的实测值[16,23],则在高维特征空间中建立的最终回归函数为

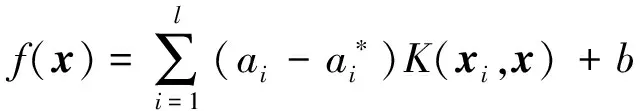
(3)

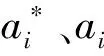
选择径向基核函数作为SVM核函数,径向基核函数表达式为

K(xi,x)=exp(-g‖x-xi‖2)

(4)

式中:g为核函数参数,g>0。

研究表明,惩罚因子C、核函数参数g和不敏感系数ε的合理选取决定着SVM性能[16,23]。C取值过小易导致网络欠拟合，C取值过大则网络过拟合,导致网络泛化能力差;g代表RBF带宽,g取值小则拟合误差小,但过小的g值会导致模型过拟合;ε值用于控制模型的预测能力,ε值小易导致模型欠拟合,ε值大则易导致模型过拟合。本文基于libsvm工具箱,利用MGTLO算法优化SVM的参数C、g和ε。

2.2 组合模型构建及实现步骤

本文提出的MGTLO-GRNN-RBF、MGTLO-GRNN-SVM、MGTLO-RBF-SVM、MGTLO-GRNN-RBF-SVM组合模型构建的基本思路是:基于GRNN、RBF、SVM模型单元两两组合及全部组合,得到GRNN-RBF、GRNN-SVM、RBF-SVM、GRNN-RBF-SVM 4种组合模型,确定各组合模型待优化目标函数和相关参数、组合权重系数搜索范围,利用MGTLO算法对各组合模型进行优化,将优化获得的最佳参数和权重系数代入各组合模型进行预测。

4种组合模型预测实现步骤可归纳如下:

步骤1选取训练样本和检验样本并对其进行归一化处理,设定组合模型σ、e、s、M、F、C、g、ε、模型单元权重系数ω的搜寻范围。由于M、F需为整数,本文采用fix函数对其进行取整。

步骤2确定各组合模型适应度函数。适应度函数是描述种群个体优劣程度的主要指标,本文选用平均相对误差绝对值之和作为适应度函数。各组合模型适应度函数描述如下：

(6)

(7)

(8)

步骤3初始化参数。设置算法最大迭代次数T,学生规模(种群)N和组数G,变量维度D及变量上、下限值;设置当前迭代次数t=0。

(9)

式中:fg为学生Xg的适应度值。如果fbest=0,那么Tg被赋值1。

步骤5随机分配给该组中每个成员一个合作伙伴,利用下式生成潜在学生Xnew:

(10)

式中:r、r′ 为[0,1]之间生成的随机向量;Xp为Xg的合作伙伴;ag为参数,如果fg优于Xp的适应度值fp,则参数ag=-1;否则,参数ag=1;Eg为[1,2]上随机选择的探索因子。

步骤6对潜在学生Xnew进行约束,并计算其适应度值fnew,如果fnew优于fg,则Xnew代替Xg,否则舍去Xnew。

步骤7合并所有组学生,并确定所有组学生中适应度值最好的学生作为教师。

步骤8令t=t+1,判断算法是否达到最大迭代次数T。若达到,则输出所有组学生中最佳适应度值及对应教师;否则转至步骤4,直到满足算法终止条件,算法结束。

步骤9输出教师所处空间位置及所对应的适应度值,即待优化问题最优解及最优适应度值。

步骤10将MGTLO算法优化获得的σ、e、s、M、F、C、g、ε和权重系数ω代入各组合模型进行预测。

3 算例分析

3.1 数据来源

3.1.1算例1

以新疆伊犁河雅马渡水文站径流预测为例进行实例分析,数据来源参见文献[24]。影响径流预测的4个预报因子分别为:X1为前1年11月至当年3月伊犁气象站的总降水量;X2为前1年8月欧亚地区月平均纬向环流指数;X3为前1年6月欧亚地区月平均径向环流指数;X4为前1年6月2 800 MHz太阳射电流量。

为便于与相关文献[24-28]进行对比,将X1～X4作为年径流量预测的影响因子,以前17年实测资料为训练样本,后6年资料作为预测样本,并利用下式对该站各径流序列进行归一化处理:

(11)

3.1.2算例2

以云南省某水文站1962—2005年44年的实测资料为例进行实例研究,利用SPSS软件分析该站年径流量与1—10月月均流量的相关性,分析结果见表3。

从表3可以看出,年径流量与1—10月月均流量均呈正相关关系,相关系数在0.056～0.727之间,相关性并不十分显著。本文选取在0.01水平(双侧)上显著相关的该站5—10月月均流量作为年径流量预测的影响因子,以1962—1991年共30年实测资料为训练样本,1992—2005年共14年资料为预测样本,利用式(11)对该站各径流序列进行归一化处理。

表3 年径流量与1—10月月均流量的相关系数

注:“**”表示在0.01水平(双侧)上显著相关;“*”表示在0.05水平(双侧)上显著相关。

3.2 模型构建与参数设置

3.2.1模型构建

基于Matlab R2011b软件环境创建4输入、1输出的MGTLO-GRNN-RBF、MGTLO-GRNN-SVM、MGTLO-RBF-SVM、MGTLO-GRNN-RBF-SVM组合模型及MGTLO-GRNN、MGTLO-RBF、MGTLO-SVM、GRNN、RBF、SVM单一模型对雅马渡水文站年径流量进行预测,创建6输入、1输出的4个组合模型和6个单一模型对云南省某水文站年径流量进行预测。选取平均相对误差绝对值(MRE)和均方根误差(R)对各模型的预测效果进行评价。

3.2.2参数设置

两个算例的参数设置均相同,即MGTLO算法T=100,N=50,G=5。各模型待优化参数搜索空间设置为:σ∈[0.000 1,10]、e∈[0.001,10]、s∈[0.001,10]、M∈[1,100]、F∈[1,100]、C∈[2-10,210]、g∈[2-10,210]、ε∈[2-10,210]、V=5。MGTLO-GRNN-RBF、MGTLO-GRNN-SVM、MGTLO-RBF-SVM、MGTLO-GRNN-RBF-SVM模型D分别为6、5、8和10;权重系数搜索空间见2.2节中的设定值。

3.3 预测结果

3.3.1算例1

利用MGTLO-GRNN-RBF、MGTLO-GRNN-SVM、MGTLO-RBF-SVM、MGTLO-GRNN-RBF-SVM组合模型及MGTLO-GRNN、MGTLO-RBF、MGTLO-SVM、GRNN、RBF、SVM单一模型对雅马渡水文站年径流量进行预测,预测结果见表4,MRE与文献[24-28]结果的对比见表5,23年的拟合和预测效果见图1。

MGTLO-GRNN-RBF模型优化结果如下:f1=118.57、σ=0.005 1、e=7.696 2、s=10.0、M=1、F=1、ωGRNN=0.393 1;MGTLO-GRNN-SVM模型优化结果如下:f2=135.12、σ=0.004 7、C=26.916 0、g=2-7.754 8、ε=2-10、ωGRNN=0.103 6;MGTLO-RBF-SVM模型优化结果如下:f3=139.47、e=0.001 0、s=3.619 4、M=39、F=30、C=22.973 4、g=2-3.995 6、ε=2-8.919 1、ωRBF=0.177 6;MGTLO-GRNN-RBF-SVM模型优化结果如下:f4=115.26、σ=0.005 1、e=9.777 0、s=9.963 6、M=1、F=100、C=26.753 5、g=22.615 3、ε=2-9.932 7、ωGRNN=0.167 2、ωRBF=0.233 1;MGTLO-GRNN模型优化结果如下:f5=205.75、σ=0.164 7;MGTLO-RBF模型优化结果如下:f6=158.30、e=8.37、s=1.472 2、M=57、F=7;MGTLO-SVM模型优化结果如下:f7=154.84、C=2-0.723 7、g=20.365 7、ε=2-10;GRNN模型优化结果如下:σ=0.50;RBF模型优化结果如下:e=10、s=0.5、M=20、F=5;SVM模型优化结果如下:C=25、g=2-5、ε=2-3。

表4 新疆伊犁河雅马渡站年径流量预测结果

表5 MRE值与相关文献预测结果比较

图1 新疆伊犁河雅马渡站年径流量拟合和预测效果

3.3.2算例2

利用4种组合模型及6种单一模型对云南省某水文站年径流量进行预测,预测结果见表6,44年的拟合和预测效果见图2。

MGTLO-GRNN-RBF模型优化结果如下:f1=72.37、σ=0.014 4、e=0.001 0、s=9.999 4、M=12、F=18、ωGRNN=0.204 7;MGTLO-GRNN-SVM模型优化结果如下:f2=76.67、σ=0.013 2、C=28.160 7、g=2-9.938 6、ε=2-7.592 2、ωGRNN=0.162 0;MGTLO-RBF-SVM模型优化结果如下:f3=49.15、e=0.001 0、s=0.353 0、M=84、F=49、C=28.668 9、g=2-10、ε=2-7.912 9、ωRBF=0.385 8;MGTLO-GRNN-RBF-SVM模型优化结果如下:f4=50.44、σ=0.027 5、e=0.076 0、s=0.435 2、M=1、F=7、C=22.675 2、g=2-4.975 7、ε=2-4.999 2、ωGRNN=0.147 2、ωRBF=0.043 3;MGTLO-GRNN模型优化结果如下:f5=127.49、σ=0.123 4;MGTLO-RBF模型优化结果如下:f6=83.68、e=0.001 0、s=0.708 6、M=33、F=43;MGTLO-SVM模型优化结果如下:f7=102.26、C=20.858 0、g=2-3.693 0、ε=2-5;GRNN模型优化结果如下:σ=0.30;RBF模型优化结果如下:e=20、s=1、M=100、F=10;SVM模型优化结果如下:C=210、g=2-4、ε=2-4。

表6 云南省某水文站年径流量预测结果

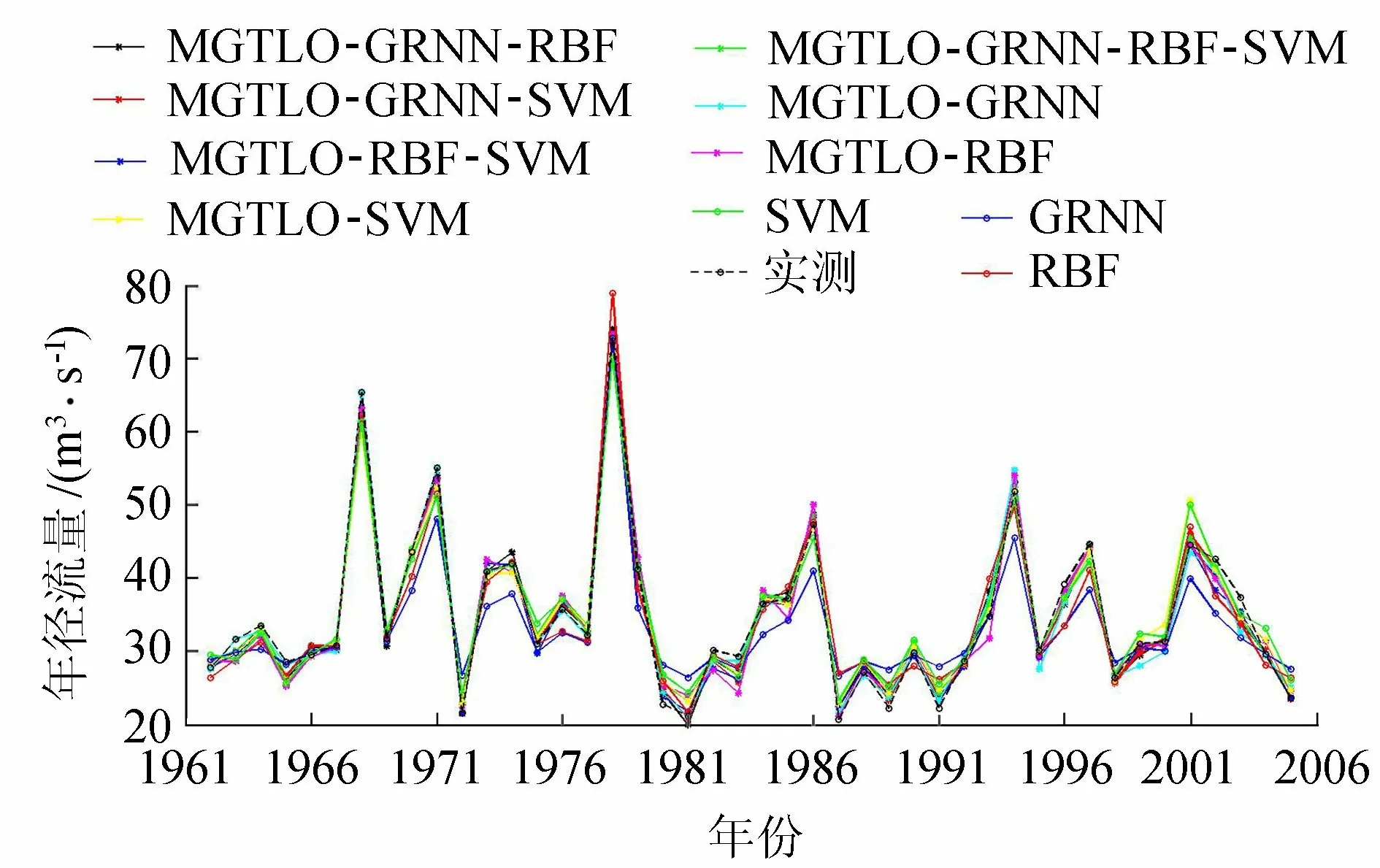
图2 云南某水文站年径流量拟合和预测效果

3.4 预测结果分析

由表4～表6及图1和图2可以看出:

a. 对于算例1,4种组合模型预测的平均相对误差绝对值在3.28%～4.70%之间,均方根误差在21.0～23.0之间,优于6种单一模型和文献[24-28]的预测精度,尤以MGTLO-GRNN-RBF-SVM模型预测效果最好；对于算例2,4种组合模型预测的平均相对误差绝对值在2.10%～3.23%之间,均方根误差在1.15～1.70之间,优于6种单一模型,尤以MGTLO-GRNN-RBF-SVM模型预测精度最高,表明MGTLO-GRNN-RBF-SVM组合模型能有效融合GRNN、RBF、SVM模型单元的优点,利用MGTLO算法优化GRNN、RBF、SVM模型相关参数和GRNN权重系数ωGRNN、RBF权重系数ωRBF能有效提高组合模型的预测精度和泛化能力。组合的模型单元数越多,预测效果越好,但同时对优化算法的寻优能力要求也较高。

b. 从各组合模型预测效果和适应度函数寻优值来看,适应度函数值越小,各单一模型间的互补性越强,组合模型的预测精度越高,表明MGTLO算法能有效优化各组合模型相关参数和权重系数。

c. 从图1和图2来看,组合模型对训练样本和预测样本具有较好的拟合和预测效果。对于单一模型,MGTLO-GRNN模型的拟合效果好,但泛化能力差,表现出过拟合特征;MGTLO-RBF模型的拟合效果差,但预测效果好,表现出欠拟合特征;MGTLO-SVM模型拟合、预测效果均较好,但拟合、预测效果劣于各组合模型。

d. 从两个实例预测效果来看,MGTLO-GRNN、MGTLO-RBF、MGTLO-SVM模型预测精度均优于其对应的GRNN、RBF、SVM模型,表明MGTLO能有效优化GRNN、RBF、SVM关键参数,优于传统的人工试凑法。

4 结 论

a. 通过5个典型测试函数对MGTLO算法进行仿真验证,并与基本TLBO算法以及SFLA、DE、PSO算法的仿真结果进行对比,结果表明MGTLO算法具有较好的寻优精度、收敛速度和全局极值寻优能力,是一种全新高效的全局优化算法。

b. 利用MGTLO算法优化基于GRNN、RBF、SVM模型单元的组合模型的适应度函数以获得各组合模型的相关参数和权重系数,提出MGTLO-GRNN-RBF、MGTLO-GRNN-SVM、MGTLO-RBF-SVM、MGTLO-GRNN-RBF-SVM组合预测模型。实例预测结果表明,组合模型能有效融合MGTLO算法和GRNN、RBF、SVM模型单元的优点,从而大大提高了组合模型的预测精度;MGTLO-GRNN-RBF、MGTLO-GRNN-SVM、MGTLO-RBF-SVM、MGTLO-GRNN-RBF-SVM组合模型用于年径流量预测是合理可行的,模型具有较好的预测精度和泛化能力,是提高预测精度的有效方法。

c. 从MGTLO算法优化各组合模型适应度函数获得的结果来看,其适应度函数值越小,组合模型的预测效果越好,其中尤以MGTLO-GRNN-RBF-SVM模型预测精度最高,表明MGTLO算法能有效优化各组合模型的相关参数和权重系数;组合的模型单元越多,预测效果越好。