基于节点移动的WSNs覆盖修复算法
2019-08-02刘丽娟刘定一廖建锋
刘丽娟, 刘定一, 廖建锋
(1. 信阳农林学院 信息工程学院, 河南 信阳 464000;2. 河南警察学院 信息安全系, 河南 郑州 450046;3. 河南经贸职业学院,河南 郑州 450046)
0 引 言
由微型传感节点构成的无线传感网络(Wireless Sensor Networks, WSNs)已在工业、农业以及医疗领域广泛使用[1-2]。基于WSNs的应用是以数据为中心。传感节点感测其覆盖范围内的数据,然后将数据向信宿传输,信宿再将数据传输至控制中心。控制中心再依据收集的数据对监测区域是否发生异常事件进行判断。
由于传感节点属微型设备,节点能量供给、数据处理以及通信半径均受限。当在监测区域部署了传感节点后,节点可能因为能量耗尽或故障失效,就无法感测原本其覆盖范围内数据,形成覆盖空白区域[3]。
覆盖空白区域[4]不但无法监测空白区域内的数据,也割裂了网络,阻碍了网络内数据传输的流畅性。因此,在形成了覆盖空白区域后,通过邻近节点的移动,覆盖这些空白区域。即对覆盖空白区域进行修复。如何选择这些修复节点成为WSNs覆盖修复算法的关键[5]。此外,WSNs经常部署于野外、人不便以介入的恶劣环境。这就给提高网络覆盖率,修复空白区域提出了挑战[6-8]。
据此,提出新的修复覆盖空白区域算法,记为RCHA(Repair-Coverage Hole Algorithm, RCHA)。RCHA先依据节点属性,包括节点能量、位置,计算节点成修复节点的概率,再依据概率择优选择修复节点。最终,通过修复节点的移动修复空白区域。仿真数据表明,提出的RCHA算法有效提高了覆盖区域。
1 网络模型及问题描述
1.1 网络模型
在区域Ω内有n个移动节点,区域面积为A2。第i个移动节点si的感测半径、通信半径分别表示为Ri、Ci。不失一般性,通信半径是感测半径的一倍,如图1所示。本文考虑同构网络,假定n个移动节点具有相同的通信半径和感测半径,即满足式(1):
Ri=Rj=R,Ci=Cj=C,i≠j,i,j=1,…,n
(1)
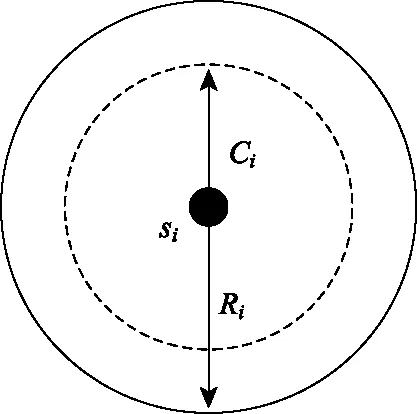
图1 传感节点的通信半径和感测半径
节点通过发送Hello消息获取邻近的局部拓扑信息,并形成自己的邻居节点集。令Ni表示节点si的邻居集,如式(2)所示:
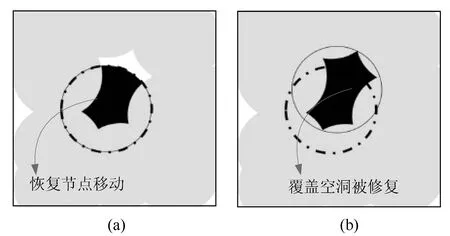
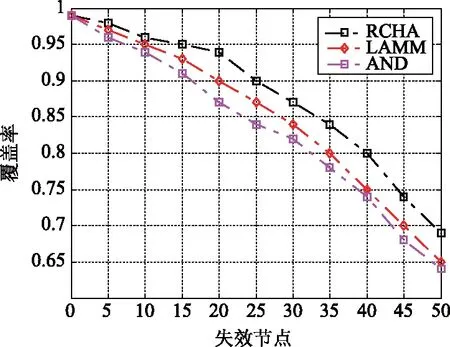
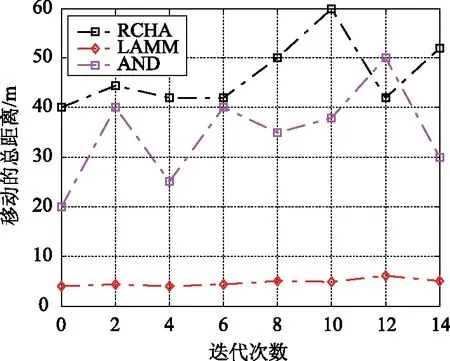
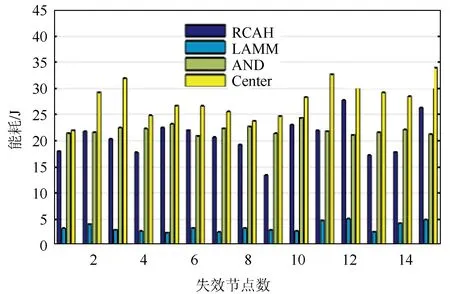
Ni={j|dij (2) 其中dij表示节点si与sj的欧式距离。 引用6元组表示节点的属性信息。令Mi=〈IDi,R,C,Li,Ei,Ni〉表示节点si的6元组信息。其中IDi、Li、Ei、Ni表示分别表示节点标识号、位置、能量以及邻居节点集。传感节点通过全球定位系统(Global Position System, GPS)获取自己位置[9]。 如图2所示,节点因能耗、故障等原因失效,而形成覆盖空白区域。图2中的空白区表示节点覆盖空白区域。 图2 覆盖空白区 提出RCHA算法的目在于修复覆盖空白区。具体而言,从覆盖空白区周边寻找合适的邻居节点,并通过此邻居节点的移动修复空白区,使原来空白区被覆盖,如图3所示。修复节点通过移动覆盖原空白区。黑色区域表示由修复节点重新覆盖的区域。 图3 覆盖空白区修复 综上所述,RCHA算法主要解决两个问题:修复节点的选择;修复节点如何移动,进而修复空白区。 RCHA算法通过节点能量、修复空白区所移动的距离以及覆盖重叠率信息,计算节点成为修复节点的概率。 若某一区域由两个或两个以上节点同时覆盖,则该区域覆盖重叠。从节点角度上讲,若两个或多个节点的覆盖区域面积有相交地方,则认为这些节点的覆盖区域重叠。对于网络而言,若网络区域覆盖重叠面积越多,节点的利用率就越低。尽可能减少节点间的覆盖重叠面积,进而提高资源利用率。 先计算两个节点的重叠区域面积。由图1可知,传感节点的覆盖区域为圆形。对于任意的两个节点(si、sj),它们的覆盖区域为两个圆。圆心为它们的位置,半径为其它们的感测半径Ri=Rj=R。若它们的圆心相距为dij,则它们的覆盖重叠区域面积: (3) 由于Ri=Rj=R,式(3)可简化为: (4) 对于传感节点si,其覆盖重叠率λi的定义如式(5)所示: (5) 为了修复覆盖空洞,修复节点需要寻找最优的移动距离以及目标位置。因此,每个节点计算需要移动的距离。再通过些距离来选择最合适的修复节点。 修复节点需通过移动, 才能覆盖空白区。因此, 移动距离是选择修复节点的重要参考量。首先, 邻覆盖空白区的邻居节点, 计算它与覆盖空白区的交叉点, 并获取这些交叉点位置,并保存离自己最近和最远的交叉点位置,如图4所示。 图4 交叉点及移动距离示意图 然后, 传感节点再依据最远交叉点和自己的位置计算所需要移动的距离Md: (6) 其中(xi,yi)表示传感节点位置。而(xp,yp)表示最远交叉点位置。 首先, 每个传感节点先计算与覆盖空白区交叉点位置, 并将这些节点信息传输至邻居。再依据最远交叉点位置, 并依据式(6)计算覆盖空白区所需移动的距离。随后, 再利用式(5)计算覆盖重叠率。 当获取了移动距离Md和覆盖重叠率λi,并结合节点剩余能量计算节点成为修复节点的概率, 如式(7)所示: (7) 其中Ei为节点si的剩余能量。从式(7)可知, 剩余能量越大, 节点成为修复节点的概率越大。能量越多, 节点能继续工作的时间越长, 具有修复覆盖空白区的能力越强。 最后, 再选择具有最大概率的节点作为修复节点, 并由它修复空白区。整个流程如图5所示。 图5 修复覆盖空白区的流程 为了更好地分析RCHA算法的性能, 通过Maltab建立仿真平台。在A2=400 m2内部署100个传感节点, 且感测半径R=50 m、通信半径C=25 m。节点能量的初始能量服从1~100 J的随机分配。假定传感节点每移动一米所消耗的能量为2 J[12]。 同时, 选择基于限制移动的动态覆盖(Limited Autonomous Mobility for Dynamic Coverage Maintenance, LAMM)算法[10]、自适应修复(Alternative Node Deployment, AND)算法[11]作为参照, 并对比分析LAMM、AND和RCHA算法的性能。 3.2.1实验一 先分析失效节点数对网络覆盖率的影响。图6显示了RCHA、LAMM和AND算法的覆盖率随失效节点数的变化情况。 图6 覆盖率 从图6可知, 失效节点数的增加, 降低了覆盖率。这主要是因为: 失效数越多, 网络内工作的节点数越少, 因此, 覆盖面积越少。此外, 相比于LAMM和AND算法,RCHA算法的覆盖率最高。原因在于: RCHA算法依据节点信息择优选择修复节点。而LAMM算法接近于静态环境, 但是LAMM算法对节点的移动进行了约束。而AND算法的覆盖率略优于LAMM算法, 但是AND算法的覆盖率仍较低。 3.2.2实验二 本次实验分析算法的移动距离。在保持覆盖率的条件下, 移动的距离越短, 算法性能越好。 图7显示了RCHA、LAMM和AND算法的移动距离。从图7可知, LAMM算法移动的距离最短, 但是它的覆盖率最低。换而言之, LAMM算法是低的覆盖率换取短的移动距离。然而, RCHA算法移动的距离最长。原因在于: RCHA算法旨在修复覆盖空白区。通过节点的移动, 修复空白区。 图7 移动距离 3.2.3实验三 本次实验分析算法的能耗, 并添加文献[12]的Center算法作为参照, 对比分析RCHA、LAMM、AND算法和Center算法的能耗性能, 如图8所示。 图8 能耗 从图8可知, LAMM算法的能耗最低。原因在于: LAMM算法移动的距离最短, 但其覆盖率低。而相比于LAMM算法和AND算法, RCHA算法的能耗较高, 这主要是因为: RCHA算法为了修复空白区, 大量节点需要移动。而Center算法的能耗最高。 针对WSNs的覆盖空白区的问题, 提出基于节点移动的覆盖空白区的修复算法RCHA。RCHA先收集覆盖空白区域信息, 并选择最优的节点修复空白区。通过节点的剩余能量, 移动距离以及覆盖重叠率信息计算节点成为修复节点的概率, 再依据概率选择最优的节点修复空白区。 通过仿真实验证实, 提出的RCHA算法以短移动距离修复了空白区。然而, 该算法存在不足: 能耗较大。这将是后期的研究内容, 降低能耗, 实现覆盖空白区的修复。1.2 问题描述
2 RCHA算法
2.1 覆盖重叠率
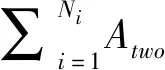
2.2 移动距离

2.3 修复节点的选择

3 性能分析
3.1 仿真平台
3.2 数值分析
4 结 语
