正整数n的分部量不小于2的有序分拆数
2019-08-02唐保祥任韩
唐保祥,任韩
(1.天水师范学院数学与统计学院,甘肃 天水 741001;2.华东师范大学数学系,上海 200062)
正整数的分拆理论是组合数学的研究课题之一,此问题在密码学,化学,生物学,统计学等学科中有广泛应用。目前,一些学者研究分部量有限制条件的有序和无序分拆数,分拆恒等式的组合证明等方面取得了丰富的研究成果[1-7]。本文利用递推的方法给出了各分部量不大于2和各分部量不小于2分拆分拆的显式计数公式,并给出了各分部量不大于3和4的分拆数的递推式,而且可以类似地给出了正整数n的各分部量是2,或3,或4的分拆数的递推式[8-10]。
1 结果及其证明
定理1设f(n)是正整数n的各分部量为1或2的分拆数;g(n+2)是正整数n+2的各分部量不小2的分拆数,则
(i)f(n)=g(n+2);
证明(i) 设An是正整数n的各分部量是1或2的所有分拆形成的集合;Bn+2是正整数n+2的各分部量不小2的分拆形成的集合。下面证明:|An|=|Bn+2|。
正整数的一个分拆唯一对应着各项是正整数的一个有限项的数列,所以在证明中为了说话方便,就把An和Bn+2中的元素就说成一个数列。
∀x∈An,在数列x的最后一项之后添加一项2,所得的数列记为y,再把y中每个2之前的相继出现的若干个1加到这个2上成为一项,所得的数列记为z,则z∈Bn+2。如,1,2,1,1,2→1,2,1,1,2,2→3,4,2。
对x1,x2∈An,当x1≠x2时,设x1=(an,an-1,…,a2,a1),x2=(bm,am-1,…,b2,b1),其中ai=1,或2,bj=1,或2,则z1=(an,an-1,…,a2,a1,2),z2=(bm,am-1,…,b2,b1,2)。假设n≤m,在a1与b1,a2与b2,…,an与bn中第一个不相等的数对是ak与bk,不妨设ak=1,bk=2,无论是a1=b1=a2=b2=…=ak-1=bk-1=1,或2,则由z1,z2的定义知,z1≠z2,且z1,z2∈Bn+2。这样就确定了An到Bn+2的一个单射,使得f(x)=z。

因此f是An到Bn+2的一个双射。故|An|=|Bn+2|,即f(n)=g(n+2)。

易知f(1)=1,f(2)=2。故


定理2(i) 设正整数n的各分部量不大于3的有序分拆数为σ(n),则
σ(n)=σ(n-1)+σ(n-2)+σ(n-3)
其中n≥4,σ(1)=1,σ(2)=2,σ(3)=4;
(ii) 设正整数n的各分部量不大于4的有序分拆数为τ(n),则
τ(n)=τ(n-1)+τ(n-2)+
τ(n-3)+τ(n-4)
其中n≥5,τ(1)=1,τ(2)=2,τ(3)=4,τ(4)=15。
证明(i) 设Ai表示正整数i的各分部量不大于3的有序分拆的集合,当n≥4时,Ai≠∅,i=n-3,n-2,n-1,且Ai∩Aj=∅(n-3≤i 故|An-3∪An-2∪An-1|=|An-3|+|An-2|+|An-1|≤|An|。 另一方面,∀z=(d1,d2,d3,…,dq)∈An,若d1=3,则(d2,d3,…,dq)∈An-3;若d1=2,则(d2,d3,…,dq)∈An-2;若d1=1,则(d2,d3,…,dq)∈An-1。 故|An|≤|An-3∪An-2∪An-1|=|An-3|+|An-2|+|An-1|≤|An|。 所以|An|=|An-1|+|An-2|+|An-3|,即 σ(n)=σ(n-1)+σ(n-2)+σ(n-3) 当1≤n≤6时,各分部量不大于3的有序分拆如下: n=1→1。 共1个。 n=2→1,1; 2。 共2个。 n=3→2,1; 1,1,1; 1,2; 3。 共4个。 n=4→3,1;2,1,1; 2,2;1,2,1;1,1,1,1;1,1,2;1,3。共7个。 n=5→3,1,1;3,2;2,2,1;2,1,1,1;2,1,2;2,3;1,3,1;1,2,1,1;1,2,2;1,1,2,1;1,1,1,1,1;1,1,1,2;1,1,3。共13个。 n=6→3,2,1;3,1,1,1;3,1,2;3,3;2,3,1;2,2,1,1;2,2,2;2,1,2,1;2,1,1,1,1;2,1,1,2;2,1,3; 1,3,1,1;1,3,2;1,2,2,1;1,2,1,1,1;1,2,1,2;1,2,3;1,1,3,1;1,1,2,1,1;1,1,2,2;1,1,1,2,1;1,1,1,1,1,1;1,1,1,1,2;1,1,1,3。共24个。 故σ(1)=1,σ(2)=2,σ(3)=4。 (ii) 的证明类似于(i)。 定理3(i) 设正整数n的各分部量是2,或3的有序分拆数为φ(n),则 φ(n)=φ(n-2)+φ(n-3) 其中n≥5,φ(2)=1,φ(3)=1。 (ii) 设正整数n的各分部量是2,或3,或4的有序分拆数为δ(n),则 δ(n)=δ(n-2)+δ(n-3)+δ(n-4) 其中n≥6,δ(2)=1,δ(3)=1,δ(4)=2。 证明仅证明(ii)。设Ai表示正整数i的各分部量是2,或3,或4的有序分拆的集合,当n≥6时,Ai≠∅,i=n-4,n-3,n-2,且Ai∩Aj=∅(n-4≤i 故|An-4∪An-3∪An-2|=|An-4|+|An-3|+|An-2|≤|An|。 另一方面,∀z=(d1,d2,d3,…,dq)∈An,若d1=4,则(d2,d3,…,dq)∈An-4;若d1=3,则(d2,d3,…,dq)∈An-3;若d1=2,则(d2,d3,…,dq)∈An-2。 故|An|≤|An-4∪An-3∪An-2|=|An-4|+|An-3|+|An-2|≤|An|。 所以|An|=|An-4|+|An-3|+|An-2|,即 δ(n)=δ(n-2)+δ(n-3)+δ(n-4) 当2≤n≤8时,各分部量是2,或3,或4的有序分拆如下: n=2→2。 共1个。 n=3→3。 共1个。 n=4→2,2;4。 共2个。 n=5→3,2;2,3。 共2个。 n=6→4,2;3,3;2,2,2;2,4。共4个。 n=7→4,3;3,2,2;3,4;2,3,2;2,2,3。 共5个。 n=8→4,2,2;4,4;3,3,2;3,2,3;2,4,2;2,3,3;2,2,2,2;2,2,4。 共8个。 故δ(2)=1,δ(3)=1,δ(4)=2。 定理2和定理3的证明思想,给出了生成正整数n的各分部量满足一定要求的正整数所有有序分拆的算法。因为递推式的解是正整数n的指数表达式,所以求各分部量满足这些的算法无有效算法。

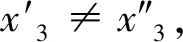


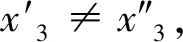
2 结 语
