基于人体骨架的非标准深蹲姿势检测方法

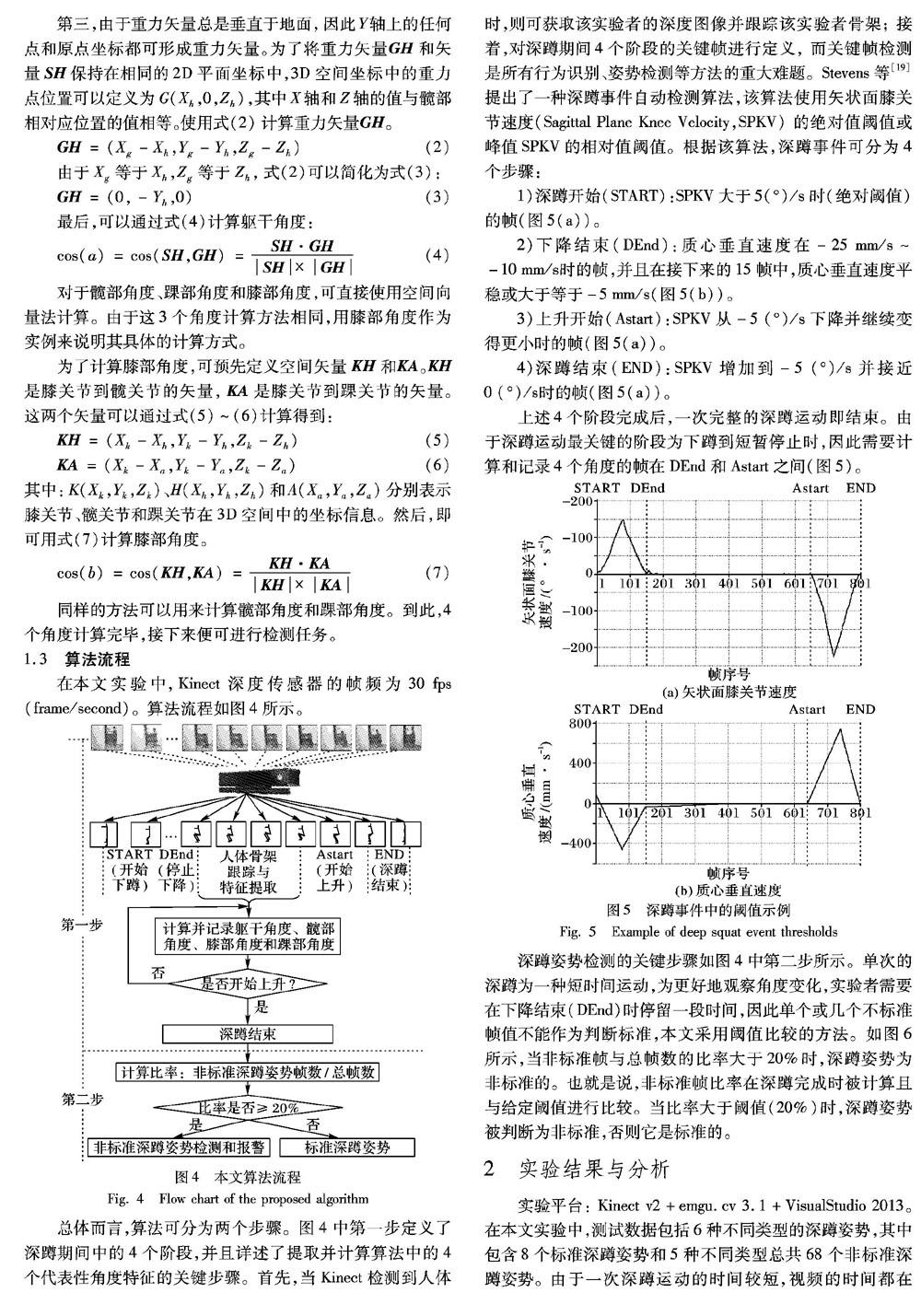
喻露 胡剑锋 姚磊岳

摘 要：针对现有的多流形人脸识别算法大多直接使用带有噪声的原始数据进行处理，而带有噪声的数据往往会对算法的准确率产生负面影响的问题，提出了一种基于最大间距准则的鲁棒多流形判别局部图嵌入算法（RMMDLGE/MMC）。首先，通过引入一个降噪投影对原始数据进行迭代降噪处理，提取出更加纯净的数据;其次，对数据图像进行分块，建立多流形模型;再次，结合最大间隔准则的思想，寻求最优的投影矩阵使得不同流形上的样本距离尽可能大，同时相同流形上的样本距离尽可能小;最后，计算待识样本流形到训练样本流形的距离进行分类识别。实验结果表明，与表现较好的最大间距准则框架下的多流形局部图嵌入算法（MLGE/MMC）相比，所提算法在添加噪声的ORL、Yale和FERET库上的分类识别率分别提高了1.04、1.28和2.13个百分点，分类效果明显提高。

关键词：多流形;降噪投影;图嵌入;最大间隔准则;分类识别

中图分类号：TP391.4

文献标志码：A

Abstract： In most existing multimanifold face recognition algorithms， the original data with noise are directly processed， but the noisy data often have a negative impact on the accuracy of the algorithm. In order to solve the problem， a Robust MultiManifold Discriminant Local Graph Embedding algorithm based on the Maximum Margin Criterion （RMMDLGE/MMC） was proposed. Firstly， a denoising projection was introduced to process the original data for iterative noise reduction， and the purer data were extracted. Secondly， the data image was divided into blocks and a multimanifold model was established. Thirdly， combined with the idea of maximum margin criterion， an optimal projection matrix was sought to maximize the sample distances on different manifolds while to minimize the sample distances on the same manifold. Finally， the distance from the test sample manifold to the training sample manifold was calculated for classification and identification. The experimental results show that， compared with MultiManifold Local Graph Embedding algorithm based on the Maximum Margin Criterion （MLGE/MMC） which performs well， the classification recognition rate of the proposed algorithm is improved by 1.04， 1.28 and 2.13 percentage points respectively on ORL， Yale and FERET database with noise and the classification effect is obviously improved.

英文關键词Key words： multimanifold; denoising projection; graph embedding; maximum margin criterion; classification and identification

0 引言

在过去十几年中，流形学习已经成为机器学习与数据挖掘领域的一个重要的研究课题[1-5]。目前，局部线性嵌入 （Locally Linear Embedding，LLE）[6]、局部保持投影 （Locality Preserving Projection， LPP）[7]、等距特征映射（ISOmetric MAPping， ISOMAP） [8]和拉普拉斯特征映射（Laplacian Eigenmap， LE）[9]等经典流形学习算法已在人脸识别和基因分类等领域得到广泛应用。之后，又有学者通过加入样本类别信息，提出了正交鉴别投影（Orthogonal Discriminant Projection， ODP）[10]、边界费舍尔分析（Margin Fisher Analysis， MFA）[11]和鉴别的局部保持投影（Discriminant Locality Preserving Projections， DLPP）[12]等算法。实际上，不同类别的样本数据差异明显，而在传统的流形学习算法中，都默认假设它们位于同一流形内，这显然是不合适的。为此，文献[13]用局部散布和类间散布来描述子流形和多流形信息，并在Fisher框架下计算投影，提出了约束最大方差映射（Constrained Maximum Variance Mapping， CMVM）算法; 文献[14]则将子流形和多流形的信息分别用类内图和类间图来表示，提出了多流形判别分析（MultiManifold Discriminant Analysis， MMDA）算法; 文献[15]提出了最大间距准则框架下的多流形局部图嵌入（MultiManifold Locally Graph Embedding based on Maximum Margin Criterion， MLGE/MMC）算法，利用图像分块的思想，对分块的小图像构建多流形，来处理小样本问题。

但是，上述多流形算法的識别性能均受到原始数据中噪声带来的影响。本文针对多流形人脸识别算法处理带有噪声的真实数据的鲁棒性问题，提出了一种基于最大间距准则的鲁棒多流形判别局部图嵌入（Robust MultiManifold Discriminant Local Graph Embedding based on Maximum Margin Criterion， RMMDLGE/MMC）算法。首先对原始数据进行迭代降噪处理，提取出更加纯净的数据;再结合多流形的思想，对数据图像进行分块，建立多流形模型;接着在最大间隔准则（Maximum Margin Criterion， MMC）的框架下，寻求最优的投影矩阵使位于不同流形上的数据样本之间的距离尽可能大，同时位于同一流形上的数据样本之间的距离尽可能小;最后通过计算待识样本流形到训练样本流形的距离进行分类识别。在ORL、Yale和FERET库上的实验，验证了所提算法的有效性。

3.6 实验结果分析

1） 在三个人脸数据集ORL、Yale和FERET的实验结果表明，随着训练样本数的增加，本文算法RMMDLGE/MMC的平均识别率均优于其他几种算法。由图5～7和图9～11可以看出，当添加噪声后，RMMDLGE/MMC的识别效果优势更加明显。

2） 在未加入噪声的Yale人脸库上，当训练样本数为2时，RMMDLGE/MMC算法的识别率比排在第二位的MLGE/MMC算法高出2.66%;在未加入噪声的FERET人脸库上，当训练样本数为3时，RMMDLGE/MMC算法的识别率比排在第二位的MLGE/MMC算法高出3.55%。因此，在训练样本数量较少时，本文所提算法RMMDLGE/MMC可以取得很好的识别效果。

3） 由表2和表3可以看出，本文算法RMMDLGE/MMC相对于其他算法在添加噪声的ORL、Yale和FERET库上的分类识别率分别提高了1.04、1.28和2.13个百分点，算法RMMDLGE/MMC的最高识别率受噪声的影响最小，充分表明它对噪声具有较强的鲁棒性。

4 结语

为了解决多流形算法对噪声的鲁棒性问题，本文提出了一种基于最大间距准则的鲁棒多流形判别局部图嵌入算法RMMDLGE/MMC。首先，通过引入一个降噪投影对原始数据进行迭代降噪处理，提取出更加纯净的数据; 再结合多流形的思想，对数据图像进行分块，建立多流形模型; 接着在最大间隔准则的框架下，寻求最优的投影矩阵使得不同流形上的样本距离尽可能大，同时相同流形上的样本距离尽可能小; 最后通过计算待识样本流形到训练样本流形的距离进行分类识别。在标准人脸图像库上的实验结果验证了本文算法的有效性。然而，在运用到实际的过程中，算法中过多的可调参数将造成参数选择问题，进一步减少算法中的可调参数将是下一步研究和改进的方向。

参考文献 （References）

[1] SEUNG H S， LEE D D. The manifold ways of perception [J]. Science， 2000， 290（5500）： 2268-2269.

[2]     MIN W L， LU K， HE X F. Locality pursuit embedding [J]. Pattern Recognition， 2004， 37（4）： 781-788.

[3]     GUI J， SUN Z N， JIA W， et al. Discriminant sparse neighborhood preserving embedding for face recognition [J]. Pattern Recognition， 2012， 45（8）： 2884-2893.

[4]     WAN M H， LI M， YANG G W， et al. Feature extraction using twodimensional maximum embedding difference [J]. Information Sciences， 2014， 274： 55-69.

[5]     AI Z H， WONG W K， XU Y， et al. Approximate orthogonal sparse embedding for dimensionality reduction[J]. IEEE Transactions on Neural Networks and Learning Systems， 2016， 27（4）： 723-735.

[6]     ROWEIS S T， SAUL L K. Nonlinear dimensionality reduction by locally linear embedding[J]. Science， 2000， 290（5500）： 2323-2326.

[7]     HE X F， YAN S C， HU Y X， et al. Face recognition using Laplacianfaces [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2005， 27（3）： 328-340.

[8]     TENENBAUM J B， SILVA V D， LANGFORD J C. A global geometric framework for nonlinear dimensionality reduction [J]. Science， 2000， 290（5500）： 2319-2323.

[9]     BELKIN M， NIYOGI P. Laplacian eigenmaps for dimensionality reduction and data representation [J]. Neural Computation， 2003， 15（6）： 1373-1396.

[10]    LI B， WANG C， HUANG D S. Supervised feature extraction based on orthogonal discriminant projection [J]. Neurocomputing， 2009， 73（1）：191-196.

[11]    YAN S， XU D， ZHANG B， et al. Graph embedding and extensions： a general framework for dimensionality reduction[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2007， 29（1）：40-51.

[12]    LIN K Z， RONG Y H， WU D， et al. Discriminant locality preserving projections based on neighborhood maximum margin [J]. International Journal of Hybrid Information Technology， 2014， 7（6）： 165-174.

[13]    LI B， HUANG D S， WANG C， et al. Feature extraction using constrained maximum variance mapping [J]. Pattern Recognition， 2008， 41（11）： 3287-3294.

[14]    YANG W K， SUN C Y， ZHANG L. A multimanifold discriminant analysis method for image feature extraction [J]. Pattern Recognition， 2011， 44（8）： 1649-1657.

[15]    WAN M H， LAI Z H. Multimanifold Locality Graph Embedding based on the Maximum Margin Criterion （MLGE/MMC） for face recognition [J].IEEE Access， 2017， 5： 9823-9830.

[16]    LI H， JIANG T， ZHANG K. Efficient and robust feature extraction by maximum margin criterion [J]. IEEE Transactions on Neural Networks， 2006， 17（1）：157-165.

[17]    HOU C， NIE F， LI X， et al. Joint embedding learning and sparse regression： a framework for unsupervised feature selection [J]. IEEE Transactions on Cybernetics， 2014， 44（6）： 793-804.

[18]    SHI J， MALIK J. Normalized cuts and image segmentation [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2002， 22（8）：888-905.

[19]    LU J， TAN Y， WANG G. Discriminative multimanifold analysis for face recognition from a single training sample per person [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2013， 35（1）： 39-51.

[20]    TURK M， PENTLAND A. Eigenfaces for recognition [J]. Journal of Cognitive Neuroscience， 1991， 3（1）：72-86.

[21]    董西偉，尧时茂，王玉伟，等.基于虚拟样本图像集的多流形鉴别学习算法[J].计算机应用研究， 2018，35（6）：1871-1878.（DONG X W， YAO S M， WANG Y W， et al. Virtual sample image set based multi manifold discriminant learning algorithm [J]. Application Research of Computers， 2018， 35（6）： 1871-1878.）

[22]    WITTEN I H， HALL M A. Data Mining Practical Machine Learning Tools and Techniques [M]. 3nd ed. San Francisco， CA： Morgan Kaufmann Publishers， 2011： 340-345.