平面闭曲线流几何演化性质的研究
2019-08-01丁丹平程永婷
丁丹平, 程永婷
(江苏大学 理学院,江苏 镇江 212013)
1 背景与问题
基于物理现象和现实问题的需要,曲线和曲面受外力的影响产生相应流的性质得到愈来愈多的关注和研究。其中收缩曲线流是其典型问题之一。即设X(s,t):[a,b]×[0,T]→R2是一族平面简单闭曲线,X0(s)=X(s,0)是初始曲线,则收缩曲线流定义为:
(1)
其中κ是曲线上点(s,t)处的高斯曲率,N是对应内法向量。1984年,Gage Hamilton证明当初始曲线为凸的平面简单闭曲线时,则在演化过程中曲线流(1)将保持凸的,并在有限时间内收缩成点[1]。1986年,Gage[2]讨论了上述平面曲线收缩流(1),得出了如果M是嵌入在平面中的凸曲线,则热方程将缩小到一个点,在某种意义上,曲线保持凸起并随收缩而变成圆形。
(2)
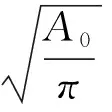
(3)
其中L,N和κ分别是长度,单位法向量和曲线的曲率。证明了平面闭凸曲线在演化过程中始终保持凸起,当减小其长度并保留闭区域时,曲线在演化过程中变得越来越圆,最后随着时间t变为无穷大其收敛到C度量中的有限圆。MIKULA K等也做了类似的工作[9-11]。
本文主要考虑如下简单闭曲线伸缩流X(s,t):S1→R2
(4)
其中T单位切向量,N单位内法向量,X0(s)是t=0时给定的平面简单闭曲线。
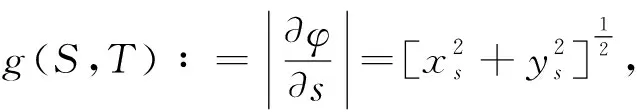
切线、法线、曲率、角度、弧长和面积由标准方法定义,即
2 若干几何量的演化控制方程
直接计算:
曲线流(3)对应的度量g、角度θ、弧长L的演化控制方程(详见[8]),即:
进一步计算,
故
(5)
(6)
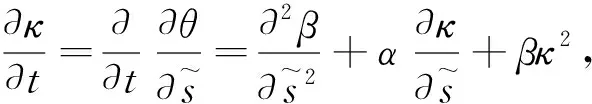
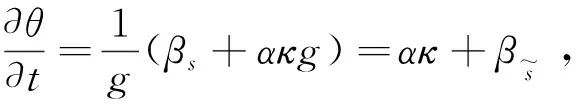
故
(7)
又因为
可得
再由(6)得到曲率κ的演化控制方程
3 弧长、面积和曲率的有界性
由(5)、(6)、(8)可知L,A,κ的演化控制方程不依赖Xt在切线上的分量。此外,我们由曲线的局部几何性质约束曲线流的形变,即β应该是曲率函数(详见[6])。假设Xt=X(.,t)是一族C2经典解曲线流,∀t∈[0,t′)(t′<),考虑α=0这一形式,即
(7)
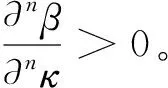
引理3.1 假设X(s,t)是(8)的解,且t∈[0,t′)(t<),那么
-2πMLt-2πm。
证明:因为β(κ)是光滑函数,所以mβ(κ)M,则有-Mκgds-βκgds-mκgds,即:-2πMLt-2πm。
引理3.2 假设X(s,t)是具有凸初值曲线(8)的一族解,如果βκ 证明: 因为β>0、βκ>0,那么 引理3.3 假设X(s,t)是(8)的解,那么曲线长度的变化速度在区间[0,2π]上是均匀的。 证明: 因此曲线长度的变化速度在区间[0,2π]上是均匀的。 引理3.4 假设X(s,t)是(8)的解,且t∈[0,t′)(t<),那么 -ML(t)At-mL(t) 证明: 即:-ML(t)At-mL(t)。 引理3.5 假设X(s,t)是一族具有凸初值条件曲线(8)的解,如果β>dκ,那么At区间[0,t′)上单调递减。 证明: 因为β>0、βκ>0、βκκ>0, 那么 与引理3.2类似,我们用反证法可以得出如果β>dκ,那么At在区间[0,t′)上单调递减,即面积的变化速度在区间[0,t′)是递增的。 引理3.6 假设X(s,t)是具有凸初值曲线(8)的一族解,那么曲线面积的变化速度在区间[0,2π]上是均匀的。 证明:计算 因此曲线面积的变化速度在区间[0,2π]上是均匀的。 因为 引理3.8 假设X(s,t)是具有凸初值曲线(8)的一族解,那么绝对总高斯曲率的变化速度在区间[0,2π]上是均匀的。 证明:计算 所以绝对总高斯曲率的变化速度在区间[0,2π]上是均匀的。 引理3.9 假设X(s,t)是(8)的解,且t∈[0,t′)(t<),那么 证明:因为β(κ)是光滑函数,所以β(κ)M。定义 这里q是f(x)=|x|的分段光滑凸近似, 那么 因为βκ>0,且q的凸性得到qκκ<0,我们有qt(t)-[q(κ)-κqκ(κ)](βκg)ds, 同时可以得到: 0q(x)-xq′(x) 因为 β(κ)M,且[q(κ)-κqκ(κ)]≥0, 因此 有 在本节中将引用[6]中的部分引理,以此证明曲线演化速度是有限的。 对于子集S⊂R2,令Nδ(S)表示δ-闭邻域,定义一个点(R2中的点)到曲线的符号距离为: 令 d(t):=d(p,Xt) 定理4.1 假设p是R2中的一点,如果C1βκC2,那么Xt是有限的。 eC1t+d(0)≥d(t)≥eC2t+d(0)。 其次,考虑点p在Xt内,此时κ(q(t))详见[6]引理4.1.2)。 则dC1d′(t)=-βdC2,那么C2C1。即: eC2t+d(o)d(t)eC1t+d(o)。 综上,Xt是有限的。

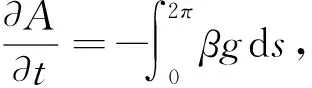
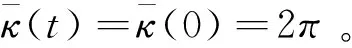


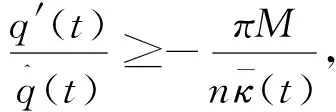


4 曲线行进的距离