喷雾干燥过程中雾滴内传质与传热方程的数值求解

张同旺，张 翊，朱丙田，刘凌涛，韩 颖，何广湘，陈海英

(1.中国石化 石油化工科学研究院，北京 100083;2.北京石油化工学院 化学工程学院，北京 102617;3.青海大学 化工学院，青海 西宁 810016)

喷雾干燥方法制备的催化剂颗粒呈球形，具有良好的流动性和耐磨性，适合在流化床中使用[1]。雾滴随热空气运动过程中，传热与传质同时进行。喷射的雾滴与热空气接触，热量以对流方式从空气传给雾滴，将水分蒸发变为汽化潜热；同时水从料雾中蒸发，蒸发的水分经过雾滴周围的边界层由对流传入空气。

蒋维钧、王喜忠等[2-3]研究发现，湿物料中的水分为非结合水和结合水，非结合水的汽化与自由液面水的汽化相当，雾滴表面温度及蒸汽分压保持不变，由表面气膜的扩散阻力控制，为恒速干燥阶段；然后是结合水的干燥，干燥速率取决于物料的性质、结构、形状尺寸，与干燥介质的流速关系不大，为降速干燥阶段，又称为物料内部迁移控制阶段。

若空气温度过高，水分很快蒸发，则雾滴内部水分迁移率不能维持雾滴表面湿润，使雾滴内的湿度梯度较大，且雾滴表面很快就形成干燥层，而干燥层又会严重阻碍水分的传递，将水分滞留在雾滴内部；传入的热量又会使雾滴内的水分气化，导致雾滴内压力升高，将干燥层崩开，使细粉增加，并有可能对所制备催化剂的微观结构产生影响[4]。因此，对喷雾干燥过程开展研究，对于生产球形度高、流化性能好、细粉量小的催化剂具有重要意义。

喷雾干燥过程中，雾滴内的传递过程与雾滴外流体(热空气)流动是既独立又相互影响的关系，二者通过雾滴表面的传热和传质相互关联。目前对于喷雾干燥的研究主要围绕喷雾干燥塔内气体的流动展开，将雾滴视为一个湿度、温度均匀的雾滴[5-6]。这与实际相去甚远，也会影响计算结果的准确性。周健[7]利用CFX的UserFortran将雾滴内传递与雾滴外流动相结合，对喷雾干燥过程进行了初步探索，但雾滴内传递方程计算速率较低。笔者目的是建立雾滴内部的传质、传热模型，并找到进行快速、准确数值计算的方法，为后续雾滴内外传递行为的耦合作准备。

1 雾滴中的传质与传热方程

1.1 传质方程

(1)

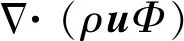
(2)

式中，C为水的质量分数，kg/kg；D为水在雾滴内的扩散系数，m2/s；r为径向位置，m。

图1 喷雾干燥催化剂电镜照片Fig.1 SEM of spray drying catalyst

催化剂制备流程如图2所示，先将分子筛、高岭土、拟薄水铝石与水混合加入剪切机分散打成浆液，然后加入盐酸剪切制成固体质量分数为20%～35%的均匀胶体，上述胶体老化12 h后制成均匀的胶体，再由喷雾干燥塔顶部雾化器雾化成中位粒径100 μm左右的小雾滴，并与热空气接触实现干燥，雾滴离开雾化喷嘴时，雾滴内各个位置处水的质量分数即为胶体中水的质量分数C0，故其初始条件为：

C(r,0)=C0

(3)

由于角方向浓度均匀，径向位置相同则水的质量分数相同，采用中心差分求浓度梯度，则雾滴中心处的浓度梯度为0[10]。雾滴表面则由于与外界存在浓度差，并且温度较高，液体气化并向雾滴外空间扩散。此处采用双膜理论，认为雾滴表面的传质速率与雾滴表面水的浓度及饱和蒸气压成正比，故式(1)的边界条件为：

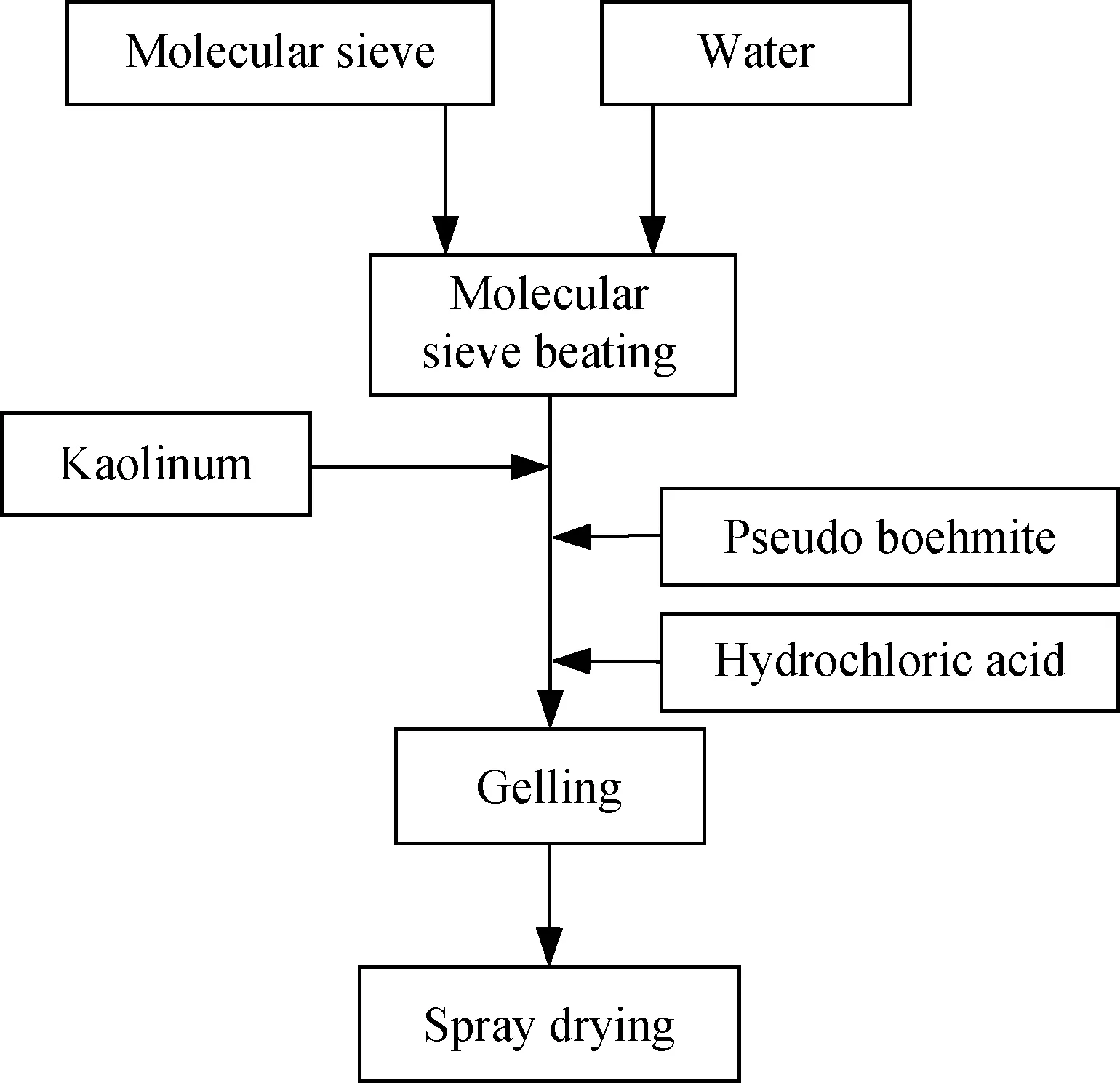
图2 催化剂制备工艺流程图Fig.2 Scheme of the catalyst preparation process

(4)

式中，R为颗粒半径，m；p为温度T下水的蒸气压，kPa；k为雾滴表面传质系数，m/(s·kPa)；kCp(T)为颗粒表面水的传质速率，kg/(m2·s)。

1.2 传热方程

与传质方程类似，传热方程有：

(5)

式中，T为温度，℃；ρ为颗粒密度，kg/m3；cp为颗粒的比热容，J/(kg·℃)；λ为导热系数，W/(m·℃)；离开喷嘴时雾滴内各处的温度相等且为物料的初始温度T0，故其初始条件为：

T(x,0)=T0

(6)

由于雾滴内角方向温度均匀，故中心处的温度梯度为0。雾滴表面温度的变化率不仅与雾滴表面的传热速率有关，还与雾滴表面液体蒸发气化吸收的热能有关，故颗粒表面的传热速率为传递进入的热量-液体气化吸收的热量，即式(5)的边界条件为：

(7)

式中，α为雾滴表面的传热系数，W/(m2·℃)；h为水的蒸发焓，J/kg。

1.3 数值求解

式(2)、式(5)形式类似，边界条件类似，且雾滴表面为第三类边界条件。赵秉新等[12-15]对形如式(2)、式(5)的数值求解方法进行了较为深入的研究，寻找高阶精度且稳定性好的离散格式，首先对空间项进行高精度离散，将方程化为各个节点上值为未知数的常微分方程组，然后对该常微分方程组应用龙格-库塔算法进行数值求解，但赵秉新等考察的边界条件均为第一类边界条件，边界处的函数值可以显式求解，而对于雾滴表面的传质与传热，均无法用显式格式直接求解。因此须将边界条件进行特殊处理，也化为关于时间项的常微分方程，并与其他节点上的值一起采用龙格-库塔方法进行求解。

1.3.1 方程离散化

由于式(2)、式(5)的形式一致，此处以式(2)为例讨论离散格式及最外层边界条件的处理。将空间划分为n-1个网格，共计n个节点，r1为颗粒中心，rn为颗粒表面。对于中心点，其导数为0，即式(2)右侧一阶偏导项为0，对右侧二阶偏导项采用二阶精度的中心差分格式进行离散，则有：

(8)

式中，C1为第1个空间离散节点上水的质量分数，即中心的浓度，C2为第2个空间节点上水的质量分数，其余类推。对于非边界点，式(2)右侧偏导项也采用具有二阶精度的中心差分格式进行离散，则各个节点离散后的格式为：

(9)

对式(2)关于最外层网格进行积分：

(10)

(11)

令：

将式(11)代入式(10)可得：

(12)

将边界条件式(4)代入式(12)可得：

(13)

Tn为颗粒表面的温度，则颗粒表面浓度的时间导数为：

(14)

将上述方法应用于传热方程式(5)和边界条件式(6)、式(7)，雾滴内传质、传热方程可化为如下的半离散常微分方程组：

(15)

1.3.2 方法验证

张亚刚等[12,16-18]将中心差分数值格式应用于有精确解的算例，用于验证该数值格式的准确性。为了验证前述数值方法的准确性，笔者将如下的初始条件和边界条件应用于式(2)，

(16)

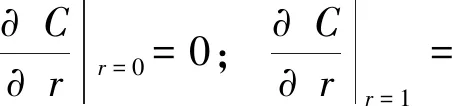
(17)

则式(2)其解析解为：

(18)

式(16)和式(17)与式(6)和式(7)同属第三类边界条件，故式(18)可用于检验前述数值方法的准确性，其相应式(15)空间离散后的常微分方程组为：

(19)

对式(19)采用龙格-库塔算法求解，令空间步长Δr=0.01 mm、D分别为0.01和0.20 mm2/s，如图3所示。D值不同，曲线的变化规律差别较大，当D=0.20 mm2/s 时，径向分布随时间、沿径向均单调下降，数值结果与解析解吻合较好；当D=0.01 mm2/s 时，径向分布为波动曲线，振幅随时间逐渐降低，还会出现不具有物理意义的负值，但数值结果依然与解析解吻合较好。这表明前述的数值求解算法能够用于求解喷雾干燥过程中雾滴内的传质与传热。

2 实际体系求解

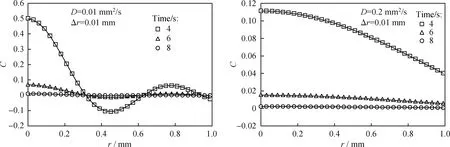
图3 数值解与解析解的比较Fig.3 The comparison between numerical and analytical solution

水的密度取值ρ=900 kg/m3，水的比热容取值为cp=4 kJ/kg，初始温度为60 ℃、雾滴的水的质量分数0.3，查物化手册得不同温度时水的饱和蒸气压，雾滴内水的质量分数和温度径向分布随时间的变化如图4 所示。

雾滴喷入流场后，雾滴内的温度急剧上升，在较短时间内即上升至系统温度；雾滴表面的水的质量分数快速降低，受扩散影响，雾滴中心处水的质量分数下降趋势相对较慢。

此处未考虑水蒸发导致环境湿度变大及其对界面处传质速率的影响；采用的扩散系数为定值，没有考虑水的质量分数降低后水的扩散速率会降低以及对水的质量分数径向分布的影响；此处的导热系数为水的导热系数，当含水量较大时，这种近似较为合理，但水量减少后，固体的导热系数的作用增加；这些都会使计算结果与实际结果有所差别，未来在对喷雾干燥塔内的流场进行计算流体力学模拟、并将雾滴内外的流场相互耦合时，须综合考虑扩散系数、导热系数，以及雾滴表面的传质系数和传热系数等随浓度的变化关系，才可能真实描述工艺条件对喷雾干燥效果的影响，进而指导工艺条件的优化。

图4 雾滴内水的质量分数与温度的分布Fig.4 The mass fraction of water and temperature in aqueous

3 结 论

(1)将广义Navier-Stokes方程应用于喷雾干燥过程中的雾滴，并进行简化，建立了雾滴的传质、传热模型。

(2)由于雾滴表面的边界条件为第三类边界，无法对雾滴表面的水的质量分数、温度进行显式求解，将边界条件与雾滴的传递模型相结合，采用中心差分格式对空间项进行离散，将传质、传热模型化为每个节点上关于时间的常微分方程组，并应用龙格-库塔法求解，建立了快速求解雾滴内浓度、温度分布的方法。以具有解析解的某个特殊方程对前述结果进行数值实验。结果表明，前述方法准确、可靠。

(3)应用前述数值求解方法求解实际雾滴内水的质量分数、温度分布，结果合理。随时间进行，雾滴温度急剧升高，雾滴表面的水的质量分数快速降低，中心的水的质量分数降低趋势相对缓和。