基于改进细菌觅食算法的测试用例生成方法

王曙燕 王瑞 孙家泽

摘 要：针对测试用例自动化生成技术中效率较低的问题，尝试引入新的细菌觅食算法，并结合测试用例生成问题提出了一种基于细菌觅食算法的改进算法（IM-BFOA）。IM-BFOA首先采用Kent映射来增加细菌的初始种群和全局搜索的多样性，其次针对算法中趋化阶段的步长进行自适应设计，使其在细菌趋化过程中更加合理化，并通过实验仿真验证其合理性，最后根据被测程序构造适应度函数来加速测试数据的优化。实验结果表明，与遗传算法（GA）、粒子群优化（PSO）算法和标准细菌觅食优化算法（BFOA）相比，该算法在保证覆盖率的前提下，在迭代次数和运行时间方面都是较优的，可有效提高生成测试用例的效率。

关键词：测试用例生成;细菌觅食算法;Kent映射;自适应步长;适应度函数

中图分类号： TP311.5

文献标志码：A

文章编号：1001-9081（2019）03-0845-06

Abstract： Aiming at the low efficiency of test case automatic generation technology， an IMproved Bacterial Foraging Optimization Algorithm （IM-BFOA） was proposed with introduction of Knet map. Firstly， Kent map was used to increase the diversity of the initial population and global search of bacteria. Secondly， the step size of chemotaxis stage in the algorithm was adaptively designed to make it more rational in the process of bacterial chemotaxis. Finally， a fitness function was constructed according to the program under test to accelerate the optimization of test data. The experimental results show that compared with Genetic Algorithm （GA）， Particle Swarm Optimization （PSO） algorithm and standard Bacterial Foraging Optimization Algorithm （BFOA）， the proposed algorithm is the best in terms of iterations number and running time with the guarantee of coverage and has high efficiency of test case generation.

Key words： test case generation; Bacterial Foraging Optimization Algorithm （BFOA）; Kent map; adaptive step size; fitness function

0 引言

軟件设计上的缺陷和代码错误严重影响了软件的可靠性和可用性，软件测试作为发现软件问题的一种方法受到了广泛关注[1]。软件测试是软件开发整个流程中必不可少的一环，也是保障软件可靠性的重要手段。软件测试可以检测软件中的bug，但软件测试耗时费力，它消耗了几乎50%的软件系统开发资源[2]。其中，测试用例生成是关键性步骤，其生成的效率决定了软件测试的整体效率，对整个软件测试工程的发展具有重要的影响。

在测试用例生成的发展过程中，根据不同的测试准则和粒度，产生了很多研究方法，主要有：数据流准则法[3]、需求分析法[4]、基于搜索的优化方法等。其中基于搜索的优化方法因其寻优能力较强而受到很多研究者的青睐，它的核心是启发式搜索算法，通过将寻找最优的测试用例问题转换为函数的最优化问题，结合生成测试用例的具体方法设计适应度函数，来实现测试用例的自动生成。Khan等[5]将遗传算法（Genetic Algorithm， GA）和变异分析方法融合来生成测试用例，该方法通过变异评分来优化测试用例，但这需要运行变异体得到变异评分，增加了运行时间。Andalib等[6]利用粒子群优化（Particle Swarm Optimization， PSO）算法生成测试用例，并将其与遗传算法进行比较，得到了更高的效率，但该方法适用于不具有数据依赖性的程序。郭后钱等[7]利用动态集合进化算法覆盖弱变异分支生成测试用例，降低减小了时间开销和测试用例规模。戚荣志等[8]利用Spark将遗传算法进行并行化，以此降低生成组合测试用例的计算成本，该方法相比串行的遗传算法得到了较高的效率。刘渊等[9]利用遗传算法生成Fuzzing测试用例，在效率和覆盖率方面得到了显著提高。夏春艳等[10]利用节点概率设计遗传算法的自适应函数来提高测试用例的生成效率。李龙澍等[11]将果蝇算法应用到测试用例领域，提高了生成测试用例的效率。这些算法都从不同的角度对测试用例生成提供了思路。

细菌觅食算法（Bacteria Foraging Optimization Algorithm，BFOA）[12]是受生物医学领域对大肠杆菌的群体觅食行为启发而总结出来的。由于BFOA群体智能算法可并行搜索、易于跳出局部极小值的优点已经吸引了不同理论研究者的注意，在电气工程与控制、调度问题、模式识别等领域得到了有效应用[13]，但该算法尚未在测试用例生成领域中实践，且该算法在寻优过程中存在收敛速度慢、精度不高的问题[14]。针对这些问题，本文引入了Kent映射[15]来增加种群多样性，并且设计自适应步长，以此来提高搜索的精度和效率。

1 测试用例生成方法

1.1 问题的编码

测试用例生成模型主要包括三部分：静态分析模块、测试驱动模块、算法生成测试用例模块。

静态分析模块 通过分析被测程序得到控制流图，选择被测程序的目标路径得到算法的部分参数，同时结合控制流图得到测试驱动模块的插桩程序。

测试驱动模块 测试驱动模块的输入为算法生成的测试用例，通过执行插桩的被测程序得到该测试用例的适应度值并传回给算法。

算法生成测试用例模块 该模块主要根据适应度值来进行判断迭代。由静态分析模块得到的参数开始执行改进的细菌觅食算法（IMproved Bacterial Foraging Optimization Algorithm， IM-BFOA），将生成的测试用例交付给测试驱动模块得到适应度值后利用IM-BFOA来迭代找到最优的测试用例。

因而，针对测试用例生成问题，首先，分析被测程序的控制流图，得到目标路径并对其进行插桩;其次，结合IM-BFOA生成初始种群，即初始的测试用例，运行插桩程序得到适应度值;最后，利用IM-BFOA迭代优化适应度值，得到更优的测试用例。

1.2 插桩方式与适应度函数的设定

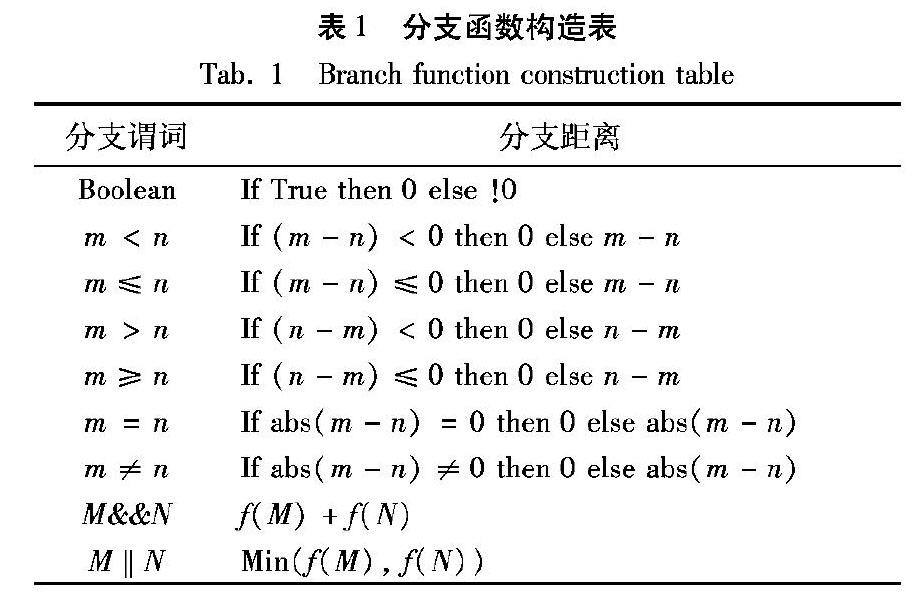
用算法解决具体的实际问题，是通过适应度函数来进行衔接，设计合理的适应度函数是更好解决问题的前提。在利用IM-BFOA解决测试用例生成问题中，适应度函数贯穿整个流程，无论是利用Kent映射产生初始种群，还是算法的趋化和复制操作，都是根据适应度值的高低决定操作步骤，而适应度值需要通过程序插桩来得到。针对不同的分支情况具体的插桩方式及分支距离如表1所示。

本文采用分支距离法[16]来评价测试用例的优劣。该方法首先需要针对分支进行插桩得到分支函数信息，现针对被测程序目标路径上的m个分支进行插桩，插桩函数如式（1）所示：

其中： f（i）表示第i个分支的插桩函数;Xi表示测试用例在第i个分支的数据;x表示分支的值。若f（i）小于等于零表示该测试用例可覆盖到该分支，则令f（i）=0;若f（i）大于零，则得到的值就是测试用例与该分支的距离，值越大代表测试用例越远离该分支。

最终计算适应度函数式如（2）所示：

式（2）使得值的范围在（0，1]区间，值越大表示测试用例越好。当适应度值为1时，表明该测试用例可完全覆盖该目标路径。

1.3 IM-BFOA生成测试用例

利用IM-BFOA生成測试用例的流程如图1所示。其中：p为测试用例问题的维度，根据被测程序导出;S是细菌初始种群;Ns是趋向操作中可前进的最大步数;C（i）是趋化操作中的游动步长;Nc是趋化操作的次数;Nre是复制操作的次数;Ned是迁徙操作的次数;Ped是细菌迁徙概率。

此流程图说明了IM-BFOA如何解决测试用例生成问题：在完成对被测程序的插桩后，利用IM-BFOA生成初始的测试用例，运行程序得到适应度值，然后经过算法的迭代优化，使适应度值达到最大值，完成基于搜索的测试用例生成。

2 细菌觅食算法

细菌觅食算法是一种新型的群体智能优化搜索算法，它模拟细菌在觅食过程中的趋化（chemotaxis）、复制（reproduction）、迁移（elimination-dispersa）三种行为。其优化搜索的操作方法如下：针对某个问题进行优化，将问题的可行域确定为其细菌的觅食区域，将问题的可行解抽象为细菌在可行域中的位置，将细菌个体的适应度转化为某个可行解针对问题是否优化的判断依据。

2.1 趋化行为

趋化行为主要靠翻转和游动两种操作来完成。翻转指的是细菌向任意方向移动单位步长的行为。游动指的是若翻转后的适应度值变高，那么将继续在同一方向进行移动，直至达到最大的游动步长或者适应度值不再得到改善;若翻转后适应度值下降，那么会继续向另一个随机的方向进行翻转。细菌的趋化行动可以用式（3）表示：

其中：θ（i， j，k，l）表示细菌i在第j次趋化、第k次复制、第l次迁移后所在的位置函数;C（i）是细菌i的趋化行动中的游动步长;Δ（i）是细菌i的趋化行动中翻转操作的单位随机方向向量。

2.2 复制行为

复制行为遵循适者生存的规律。在细菌复制前，根据适应度值降序排序，选取总细菌个数一半且适应度值高的细菌分裂成两个细菌，适应度值较低的一半细菌则被淘汰。复制行为确保了细菌种群的数量保持不变，这样可以大大提高搜索的速度。

2.3 迁移行为

迁移行为是为了防止细菌陷入局部最优点，一些细菌被随机地以小概率清除，当某个细菌满足迁移发生的概率时，该细菌就会被新的细菌所替代，新细菌是在解空间内随机初始化来的个体。迁移操作增加了细菌跳出局部最优的可能性。

3 改进的细菌觅食算法

为了解决细菌觅食算法搜索效率和精度不高的问题，引入了混沌序列，并设计了自适应步长。

3.1 Kent映射

在基本的细菌觅食算法当中，采用随机的方式来产生初细菌初始种群，这种随机性会使细菌分布不均匀，这会降低搜索的效率;因而可利用混沌序列来进行初始化，增加种群的多样性。

混沌指的是一种非线性的状态，在一定的范围内混沌变量具有随机性和遍历性。因此本文将混沌映射加入到细菌觅食算法的初始化阶段，利用混沌映射产生混沌序列。混沌序列会使得数据在某个范围内均匀分布，提高了解的质量，使得某个解尽可能地靠近最优解，从而提高算法搜索的效率。在众多的混沌映射模型当中，最基础且使用率最高的就是logistic映射，但该映射模型在遍历均匀性方面不如Kent映射[17]，因而，本文使用Kent映射来产生初始化种群，其具体计算如式（4）所示：

改进后的细菌觅食算法的初始化步骤如下。

步骤1 设置最大的迭代次数为M，种群的规模为S。

步骤4 将得到的混沌向量Y通过式（5）映射到细菌觅食算法的初始解空间：

其中：p为搜索空间的最小值，q为最大值。

步骤5 计算适应度值，选取S个最高的适应度值作为细菌觅食算法的初始种群。

3.2 自适应步长的设计

在基本的细菌觅食算法当中，不同的细菌采用的是固定的步长来进行趋化行为，而步长的大小会直接影响到细菌觅食的寻优速度和精度。如果步长较大，会使得解的精度不高;如果步长较小，算法可能会陷入局部最优，不利于算法的收敛。因而，选择合适的步长对算法而言尤为重要。

3.2.1 趋化次数的影响

对细菌觅食算法的趋化步长进行分析如下：算法初期，要求步长较大，以便尽快地搜索到最优解;随着趋化次数的增加，细菌逐步靠近最优解，需要使得搜寻的步伐减小，进行精细搜寻得到最优解，以防止步长过大而造成解震荡情况，从而提高算法的寻优速率。

根据步长随趋化次数的增加而减小的特性，利用神经网络当中的激活函数Gaussian，添加非线性因素来解决线性模型的表达能力较弱的问题，以此来解决较为复杂的问题。Gaussian激活函数原型如式（6）所示：

结合细菌觅食算法得到步长趋化次数学习因子如式（7）所示：

3.2.2 适应度值的影响

步长与细菌的适应度值有关，当细菌适应度值较小时，步长应该较大，从而使得该细菌以较大的步长进行搜寻。因而设计适应度学习因子如式（8）所示：

4 实验与分析

4.1 实验设置

为了对比分析4种方法，本实验基于eclipse平台，利用Java语言实现4种算法，并对被测程序的目标路径进行分析插桩，然后利用算法对每个被测程序独立运行多次后，统计数据得到平均值来进行实验分析。

本文实验以5个开源程序为被测对象，其详细信息见表2，从多个角度评估IM-BFOA生成测试用例的有效性。并通过与遗传算法（Genetic Algorithm， GA）、粒子群优化（Particle Swarm Optimization Algorithm， PSO）算法、基本细菌觅食算法（BFOA）、文献[10]中改进的遗传算法、文献[11]中果蝇算法的部分实验研究成果进行对比分析。

程序1的目标路径选择较为复杂的等边三角形判定;程序2的目标路径为两个数组是否相等，这里设置数组长度是4;程序3的目标路径为检验银行卡是否有效，将其长度设定为10，且选择每个代码在0～9之间，并且符合LuhnCheck算法合法的路径。程序4和程序5是两个工业用例，Sed目标路径为覆盖长选项命令行解析函数getopt_long（）的路径，Flex目标路径为计算输入的字符个数和行数。

为了保证在公平的实验环境下进行对比分析，4种方法在某些相同参数上设置一致，例如初始种群规模、最大迭代次数、独立运行次数，其他不同的参数均参考其他文献[18-20]进行设置。本文选用平均迭代次数和平均运行时间作为评判标准。具体的实验参数如表3所示。

4.2 实验分析

为了验证IM-BFOA算法中自适应步长的合理性，实验首先利用Matlab工具进行验证。设置式（9）中的参数NC=10，a=1，b=0，c=1/2π，Fmax=1，Fmin=0，C（i）=0.05，Fi分别取最大适应度值Fmax的0.25倍，0.5倍，0.75倍，得到趋化次数与步长关系如图2所示。由图可知，该自适应趋化步长在算法初期较大，有利于较快靠近最优解，随着趋化次数的增加，步长逐渐减小，可利于精细搜索，符合细菌觅食算法的要求规律，初步验证了该自适应步长设计的合理性。

同时，为了结合测试用例生成问题进行实证研究，本文通过三个对比实验来进行分析，其中在前两个实验中所有统计对比的前提条件是被测程序目标路径的覆盖率为100%。

实验一 对三角形判定程序在搜索范围为[0，5]的条件下，记录细菌的种群规模分别为10，20，30，40，50时，BFOA、IM-BFOA分别独立运行20次后的平均迭代次数和平均运行时间，实验结果如表4所示。从表4中可以看出，隨着种群规模的增加， BFOA算法与IM-BFOA算法的平均迭代次数和平均运行时间都呈现下降趋势，且IM-BFOA比基本的BFOA的平均迭代次数与平均运行时间都要少，可以看出IM-BFOA的效率更高。

实验二 在表2所示的搜索范围下，针对3个源程序，分别统计在GA、PSOA、BFOA、IM-BFOA下独立运行20次的迭代次数，得到的实验结果如图3所示。从3个程序下在不同算法的迭代情况来看，IM-BFOA所需要的迭代次数更少，寻优速度更快，能够在较少的迭代次数内找到覆盖目标路径的测试用例。

实验三 利用IM-BFOA针对表2中编号1、4、5的3个被测程序进行实验。其中，编号1的搜索范围变为[0，127]，与文献[11]保持一致，编号4、5的实验参数参考文献[10]进行设置，得到的实验结果如表5所示。与文献[11]相比，IM-BFOA在平均迭代次数和平均运行时间上均较少。与文献[10]相比，虽然本文方法的成功率较低，且在编号5中本方法的运行时间略高于文献[10]，但在其他情况下，尤其是在平均迭代次数上IM-BFOA远少于文献[10]，这是因为文献[10]在针对不可达路径的处理需要以迭代次数为代价，而本文方法针对目标路径进行处理没有检测不可达路径，这同时也导致了成功率的降低。因此，本文方法可有效生成满足覆盖目标路径的测试用例，但仍需进一步改进。

综上所述，IM-BFOA在保证被测程序目标覆盖率的前提下，生成测试用例的平均迭代次数和平均运行时间均优于GA、PSOA和BFOA，算法从整体上加快了种群的进化过程，弥补克服了算法收敛速度慢、精度不高的缺点，使得改进后算法能够快速地找到覆盖源程序目标路径的最优测试数据，有效地提高了测试用例的生成效率。

5 结语

软件自动化测试的效率主要取决于生成测试用例的效率，在利用智能群体优化算法进行搜索生成测试用例技术中，主要取决于算法的效率。本文将细菌觅食算法应用于测试用例的自动生成，并且针对基本的细菌觅食算法存在的问题，提出了一些改进措施并证明了其合理性。本文引入Kent混沌映射对细菌的初始位置进行均匀性分布，增加了种群的多样性，并且对趋化操作中的步长进行自适应设计，提高了收敛速度。同时，针对测试用例的具体问题，对算法的适应度函数进行了有效的设计，用测试用例的分支覆盖率表示适应度值，以加快测试用例的优化过程。本文利用三角形程序、判断数组相等程序和检测银行卡有效性的LuhnCheck算法程序，将遗传算法、粒子群算法、基本细菌觅食算法、改进后的细菌觅食算法进行了对比分析，实验结果表明了算法的可靠性和高效性，可以应用到测试环节中的测试用例生成问题当中。但是，相对于复杂的大规模的程序而言，其时间效率依然没有得到较大的提高，因而在后续工作中，可以利用细菌觅食算法的并行搜索能力，研究如何并行地生成测试用例，以期得到更高的效率来生成测试用例。

参考文献 （References）

[1] WU W. Research of automatic test case generation algorithm based on improved particle swarm optimization [C]// ICMMCT 2016： Proceedings of the 4th International Conference on Machinery， Materials and Computing Technology. Paris： Atlantis Press， 2016： 1558-1562.

[2] SHARMA C， SABHARWAL S， SIBAL R. A survey on software testing techniques using genetic algorithm [J]. International Journal of Computer Science Issues， 2013， 10（1）： 381-393.

[3] DENARO G， PEZZE M， VIVANTI M. Quantifying the complexity of dataflow testing [C]// Proceedings of the 8th International Workshop on Automation of Software Test. Piscataway， NJ： IEEE， 2013： 132-138.

[4] ELGHONDAKLY R， MOUSSA S， BADR N. Waterfall and agile requirements-based model for automated test cases generation [C]// Proceedings of the 2015 IEEE 7th International Conference on Intelligent Computing and Information Systems. Piscataway， NJ： IEEE， 2016： 607-612.

[5] KHAN R， AMJAD M. Automatic test case generation for unit software testing using genetic algorithm and mutation analysis [C]// Proceedings of the 2015 IEEE UP Section Conference on Electrical Computer and Electronics. Piscataway， NJ： IEEE， 2015： 1-5.

[6] ANDALIB A， BABAMIR S M. A new approach for test case generation by discrete particle swarm optimization algorithm [C]// Proceedings of the 2014 22nd Iranian Conference on Electrical Engineering. Piscataway， NJ： IEEE， 2015： 1180-1185.

[7] 郭后錢，王微微，尚颖，等.基于动态集合进化算法的弱变异测试用例集生成[J].计算机应用，2017，37（9）：2659-2664.（GUO H Q， WANG W W， SHANG Y， et al. Weak mutation test case set generation based on dynamic set evolutionary algorithm [J]. Journal of Computer Applications， 2017， 37（9）： 2659-2664.）

[8] 戚荣志，王志坚，黄宜华，等.基于Spark的并行化组合测试用例集生成方法[J].计算机学报，2018，41（6）：1064-1079.（QI R Z， WANG Z J， HUANG Y H， et al. Generating combinatorial test suite with spark based parallel approach [J]. Chinese Journal of Computers， 2018， 41（6）： 1064-1079.）

[9] 刘渊，杨永辉，张春瑞，等.一种基于遗传算法的Fuzzing测试用例生成新方法[J].电子学报，2017，45（3）：552-556.（LIU Y， YANG Y H， ZHANG C R， et al. A novel method for fuzzing test cases generating based on genetic algorithm[J]. Acta Electronica Sinica， 2017， 45（3）： 552-556.）

[10] 夏春艳，张岩，宋丽.基于节点概率的路径覆盖测试数据进化生成[J].软件学报，2016，27（4）：802-813.（XIA C Y， ZHANG Y， SONG L. Evolutionary generation of test data for paths coverage based on node probability[J]. Journal of Software， 2016， 27（4）： 802-813.）

[11] 李龙澍，郭紫梦.应用混沌果蝇算法的路径覆盖测试用例优化技术研究[J].小型微型计算机系统，2018，39（2）：362-366.（LI L S， GUO Z M. Optimization techniques research on testing data through path coverage with chaotic fruit fly algorithm [J]. Journal of Chinese Computer Systems， 2018， 39（2）： 362-366.）

[12] PASSINO K M. Biomimicry of bacterial foraging for distributed optimization and control [J]. IEEE Control Systems， 2002， 22（3）： 52-67.

[13] 周雅兰.细菌觅食优化算法的研究与应用[J].计算机工程与应用，2010，46（20）：16-21.（ZHOU Y L. Research and application on bacteria foraging optimization algorithm [J]. Computer Engineering and Applications， 2010， 46（20）： 16-21.）

[14] SADEGHIRAM S. Bacterial foraging optimisation algorithm， particle swarm optimisation and genetic algorithm： a comparative study [J]. International Journal of Bio-Inspired Computation， 2017， 10（4）： 275-282.

[15] CHEN Z， ZHOU Q. Kent chaos mapping application in the digital fountain codes [C] // Proceedings of the 30th Chinese Control Conference. Piscataway， NJ： IEEE， 2011： 4371-4376.

[16] 王令赛，姜淑娟，张艳梅，等.基于正交搜索的粒子群优化测试用例生成方法[J].电子学报， 2014， 42（12）： 2345-2351.（WANG L S， JIANG S J， ZHANG Y M， et al. Test case generation based on orthogonal exploration and particle swarm optimization [J]. Acta Electronica Sinica， 2014， 42（12）： 2345-2351.）

[17] 刘建军，石定元，武国宁.基于Kent映射的混合混沌优化算法[J]. 计算机工程与设计，2015， 36（6）： 1498-1503.（LIU J J， SHI D Y， WU G N. Hybrid chaotic optimization algorithm based on Kent map [J]. Computer Engineering and Design， 2015， 36（6）： 1498-1503.）

[18] 姜淑娟，王令赛，薛猛，等.基于模式组合的粒子群优化测试用例生成方法[J].软件学报，2016，27（4）：785-801.（JIANG S J， WANG L S， XUE M， et al. Test case generation based on combination of schema using particle swarm optimization [J]. Journal of Software， 2016， 27（4）： 785-801.）

[19] 高雪笛，周丽娟，张树东，等.基于改进遗传算法的测试数据自动生成的研究[J].计算机科学，2017， 44（3）： 209-214.（GAO X D， ZHOU L J， ZHANG S D， et al. Research on test data automatic generation based on improved genetic algorithm [J]. Compter Science， 2017， 44（3）： 209-214.）

[20] 張翼鹏，葛丽娜，王红，等.基于改进细菌觅食算法的舆情热点话题发现[J].计算机工程与设计， 2017， 38（10）： 2832-2837.（ZHANG Y P， GE L N， WANG H， et al. Cluster of people opinion analysis based on improved bacterial foraging optimization [J]. Computer Engineering and Design， 2017， 38（10）： 2832-2837.）