基于可靠信标和节点度估计距离的无线传感器网络定位算法

钱开国 卜春芬 王玉见 申时凯

摘 要：针对经典的DV-Hop、Amorphous等免测距无线传感器网络（WSN）定位算法信标节点选择不可靠、距离模糊和距离估计不准确等问题导致定位精度低，难以适应传感器节点分布不均匀应用的情况，提出了基于可靠信标和节点度估计距离的无线传感器网络定位算法（RDLA）。首先，通过跳数阈值和定位三角可靠度计算来选择引入误差小的信标节点;然后，利用节点度感知的距离估计方法计算单跳距离以解决距离模糊问题，在累积最小跳数路径（SHP）距离并修正使估计的最小跳数路径距离更准确;最后用双曲线定位方法提高定位精度。Matlab R2012a仿真结果表明：在节点均匀分布的应用中，RDLA的平均定位误差（ALE）比DV-Hop算法及其改进算法小;在节点非均匀和具有覆盖洞的C型分布的应用中，与DV-Hop算法及其改进算法相比，RDLA的ALE显著降低，几乎控制在28%以下。

关键词：无线传感器网络;免测距;节点分布;平均定位误差

中图分类号： TP391

文献标志码：A

文章编号：1001-9081（2019）03-0817-07

Abstract： Traditional DV-Hop localization algorithm and Amorphous algorithm for Wireless Sensor Network （WSN） can not meet practical application with lower localization accuracy due to defects of colinearity of beacons， range ambiguity and the distance error caused by path deviation. Especially， in the node heterogeneously distributed application scenario， the problem becomes more serious. So， a Reliable beacon-based and Density-aware distance Localization Algorithm for WSN （RDLA） was proposed to improve localization accuracy. Firstly， hop threshold and reliability function of approximate equilateral triangle were employed to select the beacon nodes with small error to avoid collinear problem. Secondly， node density-aware hop distance estimation method was used to solve range ambiguity problem， and distances were cumulatived along the Shortest Hop Path （SHP） from unknown node to three beacons. This distance was amended to straight-line distance. Finally， two-dimensional hyperbolic calculation method was adopted to determine locations of unknown nodes and improve node location accuracy. The extensive simulation results by Matlab R2012a show that the Average Localization Error （ALE） of RDLA is lower than that of DV-Hop algorithm and its improvement algorithms in node uniform distribution network. Remarkably， RDLA is tremendously superior to the others with the lowest ALE in node non-uniform distribution network and C shape network， in which， the ALE is almost controlled below 28%.

Key words： Wireless Sensor Network （WSN）; range-free; node distribution; Average Localization Error （ALE）

0 引言

无线传感器网络（Wireless Sensor Network， WSN） [1]是由部署在任务区域的大量传感器节点通过自组织方式构建的信息采集网络，可应用到健康护理、智能家居、战场监控、环境监测、目标跟踪等广阔领域中，是当前的研究热点。在大多数的应用中，传感器节点必须明确自身位置才能详细说明“在什么位置或区域发生了特定事件”，实现对外部目标的定位和追踪[2]，但由于传感器节点自身低功耗、微型化、资源有限等特点使得不可能给规模巨大的传感器节点都配置全球定位系统（Global Positioning System， GPS）设备，必须为无传感器网络设计适用的节点位置获取技术，即传感器网络节点定位。按照定位时所需的距离获取方式，已有的定位方法主要分为基于测距（Range-based）的定位算法和免测距（Range-free）的定位算法两种[3]。基于测距的定位算法通过测量未知位置节点和信标节点间的距离或方位角度，然后使用三边测量法或三角测量法计算节点位置，经典算法包括接收信号的强度指示（Received Signal Strength Indicator， RSSI）[4]、到达时间（Time-of-Arrival， TOA）[5]、到达时间差（Time Difference of Arrival， TDOA）[6]、到达角度（Angle of Arrival， AOA）[7]。这类算法需要传感器网络节点装配硬件测量模块，通过传感器节点间信号参数来测量距离，测距精度受到信号衰减、多径效应影响，同时增大了传感器节点的功耗。免测距的定位算法使用网络节点间的拓扑连接关系来估计节点间的距离，然后采用多边或者极大似然估计完成节点定位，经典的定位算法包括DV-Hop（Distance Vector Hop）[8]、Amorphous algorithm[9]、质心（Centroid）[10]定位算法、APIT（Approximate Point-In-Triangulation test）[11]。免测距定位算法不需要硬件支持，实现成本较低，功耗低，更适合资源受限的传感器网络应用;但以DV-Hop、Amorphous为代表的免测距定位算法存在距离模糊、最小跳路径偏离、信标节点共线等问题导致距离估计误差大，定位精度低。尤其在非均匀分布的应用场景中，距离估计误差更大，致使定位精度难以达到应用要求，而在传感器网络实际应用中，部署方式和障碍物使得节点分布多呈现非均匀分布，因此，在详细分析DV-Hop、Amorphous定位算法的基础上，本文根据节点分布提出了基于可靠信标和节点度估计距离的无线传感器网络定位算法（Reliable beacon-based and Density-aware distance Localization Algorithm for WSN， RDLA），降低免測距算法定位误差，并使其适用于节点非均方分布的应用中。

1 DV-Hop算法和相关研究

DV-Hop算法根据信标节点估计的平均跳距和节点间的跳数估算未知位置节点到信标节点的距离，然后利用极大似然估计法或最小二乘法计算出节点位置坐标。

1.1 DV-Hop定位算法

DV-Hop算法定位过程可分成三个阶段。首先，信标节点广播信息分组给邻居节点，該信息分组包括信标节点ID、位置坐标pi（xi，yi）、初始化为0的跳数hops。邻居节点收到该数据分组后，将跳数参数hops加1，保存并向邻居节点以广播方式转发。接收节点收到来自同一信标节点的位置信息，则保留跳数最小的信息分组，使得每个节点（包括信标节点）均保存了到所有信标节点的最小跳数和信标节点的位置信息。其次信标节点si按式（1）计算以自己为根的平均每跳距离（Average Hop Size， AHS）：

其中：hopsij是节点i到节点j的最小跳数，m是网络中部署的信标节点总数，然后信标节点将AHSi值广播给未知位置节点，通过节点存储转发，未知位置节点保存了每个信标节点的最小跳数和平均每跳距离AHS。未知位置节点从最近的信标处获得自身为根的平均每跳距离，用该平均每跳距离与最小跳数相乘就估算出未知定位节点到每个信标节点的距离。最后，未知位置节点利用极大似然估计法或最小二乘法计算自身的位置坐标。

1.2 相关算法分析

围绕定位精度的提高，研究人员提出了一些改进机制。文献[12]在经典DV-Hop算法计算出平均每跳距离AHS后，利用信标节点间的跳数与AHS相乘，估算出信标节点间的距离，利用估计距离与信标节点间的真实距离差值去除信标节点跳数和，可计算出平均每跳距离估计误差，从而修正平均跳距AHS，最后使用二维双曲线计算方法完成节点定位。文献[13]中提出一种加权处理平均每跳距离估算方法，根据到信标节点的跳数对多个信标节点的估计跳距进行加权处理，使网络平均每跳距离更为准确。文献[14]从采用最小二乘法校正信标节点的平均每跳距离、未知位置节点对收到的信标节点的平均每跳距离进行加权处理、在位置坐标估计时进行迭代求精等三项措施提高定位精度。文献[15]引入多通信半径方法细化节点间的跳数，在计算未知位置节点平均每跳距离时，剔除孤立节点，并利用信标节点得到的平均每跳距离进行加权归一化处理，来提高定位精度。文献[16]对接收到的多个信标节点平均每跳距离进行加权求和来减小平均每跳距离的误差，并且利用改进的最小二乘法来解决误差累积的问题。这些算法通过优化跳距计算，降低距离估计误差从而提高定位精度。Regulated neighborhood distance-based localization[17]算法使用了节点公共邻居数作为距离估计因子，距离估计较为精确，但当节点间跳数较大、最小跳路径偏离严重时，距离估计误差也会增大。Selective3-Anchor DV-Hop[18]用未知位置节点到信标节点间的跳数作为向量，应用向量差异最小为标准选择出三个最佳的信标节点完成未知位置节点定位，算法的距离估计仍使用DV-Hop的距离估计方法，孤立信标节点、大跳数信标节点也有机会成为参考节点。Rendered path[19]算法计算出渲染路径和直线距离的角度，从而计算出未知位置节点到信标节点的距离，提出了有效的、具有覆盖空洞的传感器网络的节点定位算法。Hop Count based Decomposition DV-Hop （HCD-DV-Hop）[20]通过传感器网络子区域划分，来降低DV-Hop算法在传感器网络非均匀分布时的定位误差，但如何划分子区域在分布较为复杂的传感器网络应用中难以确定。Improved Weighted Centroid DV-Hop （IWC-DV-Hop）[21]首先设定距离阈值来选择信标节点，去除大跳数不可靠节点，这些信标节点引入误差较大，然后使用信标节点的AHS和未知位置节点跳数相乘来估计距离，该距离和跳数作为因子，计算每个信标节点的权值，使用加权质心算法完成未知位置节点定位。文献[22]利用移动信标节点辅助定位，提高定位精度，在定位过程中，需要规划信标节点的移动轨迹。

1.3 误差来源分析

免测距定位算法DV-Hop存在3个缺陷，引入定位误差。

1.3.1 路径偏离和距离模糊问题

免测距算法在距离计算时，采用最小跳路径跳数与估算出的平均每跳距离相乘。这种距离计算方法首先用两节点间最小跳路径上的跳段距离替代节点直线路径跳数，在覆盖洞、分布不均匀等网络应用中，最小跳路径严重偏离直线路径时，将引入较大的距离估计误差，即出现路径偏离问题。如图1（a）所示，节点对u、v之间的最小跳路径为u-c-d-e-f-g-v，跳数hops为6;直线路径为u-h-v，跳数hops为2。

另外，同一节点，其外围分布的节点，如果距其跳数hops相同，则其估计距离相同，称为距离模糊问题。如图1（b）所示，信标节点z的1-hops邻居节点u、v、w被估计到z的距离相同，实际上u和w相差近节点通信半径r的距离。

1.3.2 共线问题

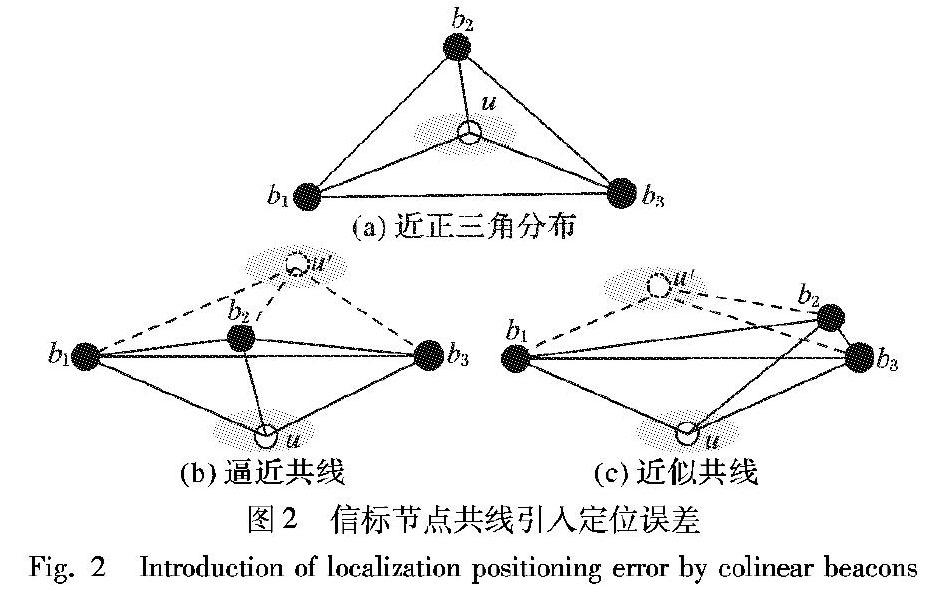
未知位置节点定位时，至少需要选择3个信标节点作为参考节点。如果选择的3个信标节点共线或逼近共线时，引入巨大的定位误差。如图2所示，阴影区域为未知位置节点u可能的定位位置，如图2（a）所示，3个信标节点近正三角形分布时，定位误差较小;而如图2（b）、（c）逼近共线分布时，如果被定位到u′阴影区域，引入的定位误差较大。

2 可靠信标和节点度估计距离的改进算法

首先设计跳数阈值来限制大跳数节点参与定位，形成候选信标节点集，再用近正三角形选择函数选择最佳分布的3个信标节点;其次，使用节点度来估计每个节点单跳距离，累积最小跳路径距离并修正该距离;最后采用双曲线定位计算完成节点定位，从而使DV-Hop算法在传感器网络应用中保持了较小的定位误差，具有较高的定位精度，同时也适用于非均匀分布的传感器网络应用。

2.1 拓扑信息交换

信标节点i生成元数据，包含自身序号、位置信息字段和跳数字段，即（id，xi，yi，hops）的四元组，其中，hops字段的初始值为0，向周围邻居节点广播出去，邻居节点接收该元数据后，将hops字段值加1，然后以泛洪方式广播出去，每个接收节点如果收到来自同一信标节点的元数据，则只保留hops字段值较小的元组数据;同时未知位置节点生成最小跳数查询元数据，包括自身序号和跳数字段，即（id，hops）的二元组，同信标节点一样的方式在全网内泛洪。通过拓扑信息交换，每个节点（包括信标节点）都记录了到其他节点所需要的最小跳数值。根据该跳数值hops（i），可构建全网的最小跳数路径拓扑结构。根据该拓扑结构，每个节点均可生成以自己为根的最小路径生成树。

2.2 信标节点选择

随机部署的无线传感器网络，传感器网络节点的分布服从泊松分布[23]，在区域A内分布的k个传感器网络节点概率密度函数为：

其中：λ=N/S为节点密度，N传感器节点数，S为监测区域面积。

因此，在未知位置节点u的n跳区域内分布的平均信标节点个数为：

其中r为传感器节点通信半径。

未知位置节点u完成定位，至少需要选择3个信标节点作为参考节点，则有：

即可求出未知位置节点最少取到3个信标节点的最近的n跳信标节点作为参考节点完成定位，即：

n3=UP-integer（1r3λπ）（5）UP-integer是一个函数名，还是UP减去integer？请明确

为了避免选择的3个信标节点共线或者逼近共线，充分利用网络中部署其余信标节点约束产生距离模糊问题。设网络监测区域直径为D，网络中存在的最大跳数为：

则取未知位置节点u的k跳邻居信标节点形成候选参考节点集：

2.3 lg（u）的距离估计

2.3.1 u到3个未知位置节点的距离估计

2.3.2 距离修正

信标节点选择完成后，定位单元lg（u）的分布有2种情况，u位于3个信标节点构成的三角形内部和u在信标节点构成的三角形外部，分别如图4（a）和图4（b）所示。

2.4 节点定位

3 实验结果与分析

为了验证算法的有效性，使用Matlab R2012a，在1000m×1000m的任务区域部署300个传感器节点，传感器节点在任务区域呈均匀随机分布、非均匀分布和C型节点分布三种应用场景中进行仿真实验，实验拓扑如图5所示。

将信标节点比例设置为10%～45%，步长增长为5%，节点通信半径设置为150～290m，步长增长为20m，两个参数变化上，对经典的DV-Hop算法、改进Improved DV-Hop （I-DV-Hop）算法[12]、IWC-DV-Hop[21]和本文改进算法RDLA定位性能进行实验对比分析。用网络的平均定位误差（Average Localization Error， ALE）比较考察算法的定位性能。平均相

3.1 节点均匀分布

图6是在节点均匀随机分布的场景中，信标节点比例和通信半径变化时，4种算法的平均相对定位误差结果。

从图6可以看出，随着信标节点比例和通信半径的增加，4种算法的定位误差均呈整体下降趋势。从图6（a）可以看出，经典的DV-Hop算法的定位精度从信标节点比例为10%的31.7%下降到信标节点比例为60%时的29%，改进算法I-DV-Hop从信标节点比例为10%时的28.9%下降到信标节点比例为60%时的24.8%，IWC-DV-Hop算法从31.5%下降到23%，而RDLA从信标节点比例为10%时的21.8%下降到信标节点比例为60%时的20.2%。总体上看，除了IWC-DV-Hop算法外，信标节点比例的提高对定位误差的影响不是很大，这是因为在节点均匀分布时，DV-Hop、改进算法I-DV-Hop和本文RDLA在跳距和距离估计时，最小跳路径基本靠近节点间直线路径，跳距估计和距离估计较为精确，只要满足有3个信标节点，定位就会比较准确，所以信标节点比例影响较小;而IWC-DV-Hop算法使用了阈值限制选择信标节点下的加权质心算法，信标节点数越多，可选择更加靠近未知位置节点的信标节点执行加权质心定位，精度就愈高。4种算法中，DV-Hop算法定位误差最高;改进算法I-DV-Hop平均跳距修正和双曲线定位计算方法提高了距离估计准确度和降低了计算误差，从而减少了定位误差;IWC-DV-Hop的加权质心定位计算方法在信标节点数较多时，获得了较高的定位精度;而本文RDLA通过正三角函数选择可靠信标，避免信标节点共线引入的误差，采用基于节点度的单跳距离估计和最小跳路径距离累积和修正的方法使距离估计接近节点间的直线距离，并用双曲线定位计算降低计算误差，从而获得最高的定位精度，且只要满足3个信标节点定位条件，信标节点个数对定位误差影响就很小。在实际应用中，就可以部署较少的信标节点来降低网络成本。

从图6（b）可以看出，随着节点通信半径提高，节点度提高，网络连通性越来越好，4种算法的定位误差均下降。经典的DV-Hop定位误差从41%减小到30.5%，改进算法I-DV-Hop从35.4%减小到27%，IWC-DV-Hop从41%降低到28%。本文的RDLA基于节点度的距离估计，减轻了距离模糊问题的影响，所以，定位性能最好，定位誤差从25.6%减小到21%左右。

3.2 非均匀分布

节点非均匀分布应用场景按照图5（b）完成节点部署，设置信标节点比例和通信半径两个参数，定位误差结果如图7所示。

随着信标节点比例从10%增加到50%，经典DV-Hop算法的定位误差从36.5%降低到32%，改进算法I-DV-Hop在30%左右波动，IWC-DV-Hop算法从37.5%降低到24.5%。随着信标节点比例增加，IWC-DV-Hop算法的阈值控制下信标节点选择机制选出引入误差下的信标节点机会大幅度增加，尤其是信标节点比例达到30%以后，其定位误差就开始低于26%;而本文RDLA由于近似正三角的信标节点选择、基于节点度的单跳距离估计和最小跳数路径距离修正保证距离估计准确。只要能选择到3个非共线节点，定位就比较精确，所以信标节点比例影响较小，定位误差几乎维持在24.5%左右，远低于其余三种算法。

隨着通信半径从150增加到290，4种算法的定位误差均降低，DV-Hop从42%降低到33%，改进算法I-DV-Hop从44%降低到29%，IWC-DV-Hop从37%降低到28%，而本文RDLA几乎维持在25%左右，定位精度较高。

对比图6和图7，从节点均匀分布到非均匀分布，4种算法的定位误差均升高，DV-Hop和改进算法I-DV-Hop升高最大。IWC-DV-Hop在信标节点比例较小时升高较大，但信标节点比例提高时升高较少。而本文RDLA升高最小，在非均匀分布时，也获得较高的定位精度，说明本文算法基于节点度的距离估估计和修正在节点非均匀分布时，距离估计也较为准确。

3.3 C型分布

按照图5（c）的应用场景完成节点部署，该节点部署方式存在覆盖洞，节点间的最小跳数路径存在严重弯曲，远偏离节点间的直线路径。

从图8可以看出：随着信标节点比例和通信半径的增加，经典的DV-Hop、改进算法I-DV-Hop算法定位误差有呈降低趋势，但由于最小跳路径偏离严重，距离估计非常不准确，引入的定位误差较大，达80%以上，难以满足定位精度的应用要求。而IWC-DV-Hop算法基于阈值完成信标节点选择后，再对信标节点到未知位置节点间的跳数路径距离进行修正后使用质心算法完成节点定位，所以定位误差相比前两个算法，改进较大，而随着信标节点比例的增加，信标节点比例为10%，定位误差最大，在50%;当信标节点在15%时，定位误差就下降到40%以下;随着信标节点比例的增加，定位误差进一步减小。本文RDLA的距离估计方法，始终比较准确，获得的定位误差也最小，无论信标节点是否增加，维持在28%左右，远低于其他三种算法。

随着节点通信半径的增加，4种定位算法的定位误差均降低。整体来看，DV-Hop和改进算法I-DV-Hop算法定位误差也非常大，大于65%;IWC-DV-Hop算法大于40%;而本文算法维持在28%左右，定位误差最小，定位精度最高。

综合图6～8来看，随着节点分布非均匀程度的增加，4种算法的定位误差均升高，但是DV-Hop、改进算法I-DV-Hop定位误差升高最大，存在有覆盖洞的极端情况C型分布中，定位误差非常大，难以满足定位精度要求;IWC-DV-Hop定位误差升高次之，在非均匀分布和C型分布时，随着信标节点比例和通信半径的增加，定位误差增加较小。而本文RDLA，近似正三角形的信标节点选择避免了共线引入误差，基于节点度的单跳距离估计减轻了距离模糊问题，而最小跳数路径距离估计和修正使距离估计使得无论在节点怎么分布时，距离估计都非常准确，所以随着节点分布非均匀度增长，定位误差尽管有所增加，但始终保持在28%以下，定位精度较高。

4 结语

针对传统的DV-Hop算法及其改进算法中存在的信标节点共线或近似共线、距离模糊和距离估计不准确等问题，在无线传感器网络节点分布较为均匀、节点密度较高的应用场景中，引入误差小，定位精度满足应用要求。当无线传感器网络节点分布不均匀，甚至存在覆盖洞等应用场景中，引入较大的定位误差，难以满足定位精度要求。本文引入基于跳数阈值和近正三角形信标节点选择避免信标节点共线，去除大跳数、不可靠的信标节点参与节点定位;并采用基于节点度的单跳距离估计缓解距离模糊问题，对最小跳数路径累计估计并进行修正，从而保证无论节点均匀分布、非均匀分布或存在覆盖洞分布情况下，距离估计均较为准确，保持较低的定位误差。

参考文献 （References）

[1] AKYILDZ I.F， SU W， SANKARASUBRAMANIAM Y， et al. A survey on sensor networks[J]. IEEE Communications Magazine， 2002， 40（8）：102-114.

[2] 王福豹，史龙，任丰原.无线传感器网络中的自身定位系统和算法[J].软件学报，2005，16（5）：857-867.（WANG F B， SHI L， REN F Y. Self-localization systems and algorithms for wireless sensor networks[J]. Journal of Software， 2005， 16（5）：857-867.）

[3] 曾凡仔，孙正章，罗娟，等.无线传感器网络的节点定位方法[J].通信学报，2008，29（11）：62-66.（ZENG F Z， SUN Z Z， LUO J， et al. Improved node localization algorithm for wireless sensor network[J]. Journal on Communications， 2008，29（11）：62-66.）

[4] ZHONG Z， HE T. Achieving range-free localization beyond connectivity[C]// Proceedings of the 7th ACM Conference on Embedded Networked Sensor Systems. New York： ACM， 2009：281-294.

[5] PATWARI N， HERO A O， PERKINS M， et al. Relative location estimation in wireless sensor networks[J]. IEEE Transactions on Signal Processing， 2003， 51（8）：2137-2148.

[6] GIROD L， ESTRIN D. Robust range estimation using acoustic and multimodal sensing[C]// Proceedings of the 2001 International Conference on Intelligent Robots and Systems. Piscataway， NJ： IEEE， 2001：1312-1320.

[7] LAZOS L， POOVENDRAN R. ROPE： robust position estimation in wireless sensor networks[C]// Proceedings of the 2005 International Symposium on Information Processing in Sensor Networks. Piscataway， NJ： IEEE， 2005：323-331.

[8] NICULESCU D， NATH B. DV based positioning in Ad Hoc networks[J]. Telecommunication Systems， 2003， 22（1/2/3/4）：267-280.

[9] JI W W， LIU Z. An improvement of DV-Hop algorithm in wireless sensor networks[C]// Proceedings of the 2006 International Conference on Wireless Communications， Networking and Mobile Computing. Piscataway， NJ： IEEE， 2006：1-4.

[10] 張爱清，叶新荣，胡海峰.无线传感器网络质心定位新算法及性能分析[J].计算机应用，2012，32（9）：2429-2431.（ZHANG A Q， YE X R， HU H F. Performance analysis of new centroid localization algorithm in wireless sensor network[J]. Journal of Computer Applications， 2012， 32（9）：2429-2431.）

[11] HE T， HUANG C， BLUM B M， et al. Range-free localization and its impact on large scale sensor networks[J]. ACM Transactions on Embedded Computing Systems， 2005， 4（4）：877-906.

[12] 石为人，贾传江，梁焕焕.一种改进的无线传感器网络DV-Hop定位算法[J].传感技术学报，2011，24（1）：83-87.（SHI W R，JIA C J， LIANG H H. An improved DV-Hop localization algorithm for wireless sensor networks[J]. Chinese Journal of Sensors and Actuators， 2011，24（1）：83-87.）

[13] 刘锋，张翰，杨骥.一种基于加权处理的无线传感器网络平均跳距离估计算法[J].电子与信息学报，2008，30（5）：1222-1225.（LIU F， ZHANG H， YANG J. An average one-hop distance estimation algorithm based on weighted disposal in wireless sensor network[J]. Journal of Electronics and Information Technology， 2008， 30（5）：1222-1225.）

[14] 林金朝，陈晓冰，刘海波.基于平均跳距修正的无线传感器网络节点迭代定位算法[J].通信学报，2009，30（10）：107-113.（LIN J Z， CHEN X B， LIU H B. Iterative algorithm for locating nodes in WSN based on modifying average hopping distances[J]. Journal on Communications， 2009，30（10）：107-113.）

[15] 景路路，张玲华.基于跳距优化的改进型DV-Hop定位算法[J].传感技术学报，2017，30（4）：582-586.（JING L L， ZHANG L H. An improved DV-Hop location algorithm based on hop-distance optimization [J]. Chinese Journal of Sensors and Actuators， 2017， 30（4）：582-586.）

[16] 赵芝璞，吴栋，王艳，等.基于平均跳距和位置优化的改进DV-Hop定位算法[J].系统仿真学报，2016，28（6）：1273-1280.（ZHAO Z P， WU D， WANG Y， et al. Improved DV-Hop localization algorithm based on average hopping distance and position optimization[J]. Journal of System Simulation， 2016， 28（6）：1273-1280.）

[17] WU G， WANG S， WANG B， et al. A novel range-free localization based on regulated neighborhood distance for wireless Ad Hoc and sensor networks[J]. Computer Networks， 2012， 56（16）：3581-3593.

[18] GUI L， VAL T， WEI A， et al. Improvement of range-free localization technology by a novel DV-Hop protocol in wireless sensor networks[J]. Ad Hoc Networks， 2015， 24： 55-73.

[19] LI M， LIU Y H. Rendered path： range-free localization in anisotropic sensor networks with holes[J]. IEEE/ACM Transactions on Networking， 2007， 18（1）：320-332.

[20] GAO B， ZHAO X， WANG J， et al. Decomposition based localization for anisotropic sensor networks[J]. International Journal of Distributed Sensor Networks， 2015， 2015： Article No. 8.

[21] SONG G， TAM D. Two novel DV-Hop localization algorithms for randomly deployed wireless sensor networks[J]. International Journal of Distributed Sensor Networks， 2015， 2015： Article ID 187670.

[22] SABALE K， MINI S. Anchor node path planning for localization in wireless sensor networks[J]. Wireless Networks， 2017（8）：1-13.

[23] HUANG B， YU C， ANDERSON G， et al. Connectivity-based distance estimation in wireless sensor networks[C]// Proceedings of the 2010 Global Telecommunications Conference. Piscataway， NJ： IEEE， 2010：1-5.

[24] HAN G， CHOI D， LIM W. Reference node placement and selection algorithm based on trilateration for indoor sensor networks[J]. Wireless Communications & Mobile Computing， 2009， 9（8）：1017-1027.

[25] SARRATR J， PALAU J， HUERTA A. Numerical representation of the quality measures of triangles and triangular meshes[J]. International Journal for Numerical Methods in Biomedical Engineering， 2003， 19（7）：551-561.

[26] KLEIN L， SILEVESTR J. Optimum transmission radii for packet radio networks or why six is a magic number[C]// Proceedings of the 1978 IEEE National Telecommunication Conference. Piscataway， NJ： IEEE， 1978：431-435.