基于阈值自适应忆阻器Hopfield神经网络的关联规则挖掘算法
2019-07-31于永斌戚敏惠尼玛扎西王琳
于永斌 戚敏惠 尼玛扎西 王琳


摘 要:针对基于Hopfield神经网络的最大频繁项集挖掘 (HNNMFI)算法存在的挖掘结果不准确的问题,提出基于电流阈值自适应忆阻器(TEAM)模型的Hopfield神经网络的改进关联规则挖掘算法。首先,使用TEAM模型设计实现突触,利用阈值忆阻器的忆阻值随方波电压连续变化的能力来设定和更新突触权值,自适应关联规则挖掘算法的输入。其次,改进原算法的能量函数以对齐标准能量函数,并用忆阻值表示权值,放大权值和偏置。最后,设计由最大频繁项集生成关联规则的算法。使用10组大小在30以内的随机事务集进行1000次仿真实验,实验结果表明,与HNNMFI算法相比,所提算法在关联挖掘结果准确率上提高33.9个百分点以上,说明忆阻器能够有效提高Hopfield神经网络在关联规则挖掘中的结果准确率。
关键词:电流阈值自适应忆阻器;Hopfield神经网络;最大频繁项集;关联规则挖掘;能量函数
中图分类号: TP301.6
文献标志码:A
文章编号:1001-9081(2019)03-0728-06
Abstract: Aiming at the inaccurate mining results of the Maximum Frequent Itemset mining algorithm based on Hopfield Neural Network (HNNMFI), an improved association rule mining algorithm for Hopfield neural network based on current ThrEshold Adaptive Memristor (TEAM) model was proposed. Firstly, TEAM model was used to design and implement synapses whose weights were set and updated by the ability of that threshold memristor continuously changes memristance value with square-wave voltage, and the input of association rule mining algorithm was self-adapted by the neural network. Secondly, the energy function was improved to align with standard energy function, and the memristance values were used to represent the weights, then the weights and bias were amplified. Finally, an algorithm of generating association rules from the maximum frequent itemsets was designed. A total of 1000 simulation experiments using 10 random transaction sets with size less than 30 were performed. Experimental results show that compared with HNNMFI algorithm, the proposed algorithm improves the result accuracy of association mining by more than 33.9 %, which indicates that the memristor can effectively improve the result accuracy of Hopfield neural network in association rule mining.
Key words: current ThrEshold Adaptive Memristor (TEAM); Hopfield Neural Network (HNN); maximum frequent itemset; association rule mining; energy function
0 引言
憶阻器的概念由蔡绍棠教授在1971年提出[1],2008年惠普实验室的研究人员Strukov等[2]首次做出实物模型,此后掀起忆阻器的研究热潮。忆阻器具有非线性和记忆特性[3],用来模拟人工神经网络中的突触[4],能够实现突触权值的连续更新并且在断电之后也能保存权值。近年来,许多忆阻器的数学模型相继被提出,其中Kvatinsky等提出电流阈值自适应忆阻器(ThrEshold Adaptive Memristor, TEAM)模型[5],该模型可通过调整系数以匹配其他忆阻器的数学模型,是一种非常精确且很有潜力的数学模型[6]。目前忆阻器的国内外研究方向主要包括神经网络、存储器、混沌电路、交叉阵列等[7]。忆阻器在神经网络中的研究取得很多进展[8-10],如电子科技大学的Hu等使用可重构忆阻离散Hopfield神经网络实现单联想和多联想记忆[11]。
Hopfield神经网络(Hopfield Neural Network, HNN)由Hopfield等在1982年提出,该模型又分为离散型(Discrete Hopfield Neural Network, DHNN)[12]和连续型(Continuous Hopfield Neural Network, CHNN)[13]。能量函数的概念被首次引入到人工神经网络中,为解决优化计算问题提供新的方法。能量函数的标准形式已由Hopfield给出,不同的优化问题对应的能量函数形式不同,但都由约束条件和目标解两个部分组成,只要能将其转化为标准形式便可从能量函数中导出权重和偏置。CHNN随时间演变,始终向能量函数降低的方向移动,最后达到能量函数的极小值点,即稳定平衡状态。将优化问题的目标函数与网络的能量函数相对应,则问题的求解过程可以看作CHNN向能量函数极小值点移动的过程。目前HNN的应用领域主要包括联想记忆和优化计算等[13]。
关联规则的概念最初是Agrawal等[14]在1993年针对购物篮分析问题(Market Basket Analysis)提出的,且于1994年提出经典的关联规则挖掘算法Apriori算法[15]。目前常见的关联规则挖掘算法[16]大致可分为:宽度优先算法如DHP(Direct Hashing and Pruning)算法[17];深度优先算法如FP-growth(Frequent-Pattern growth)算法[18];数据集划分算法如Partition算法[19];采样算法如Sampling算法[20];并行挖掘算法如CD(Count Distribution)、DD(Data Distribution)、CaD算法(Candidate Distribution)[21]等。其中FP-growth算法对Apriori算法的改进效果最显著。
Gaber等[22]提出基于Hopfield神经网络的最大频繁项集挖掘 (Maximum Frequent Itemset mining based on Hopfield Neural Network, HNNMFI) 算法,该算法属于并行挖掘算法,为CHNN在关联规则挖掘领域中的应用提供可行的思路。但该算法定义的能量函数与标准形式不太符合,权值和偏置较小,导致挖掘到的频繁项集范围小,无法适应不同大小的事务集。
本文针对上述问题,提出基于忆阻Hopfield神经网络(Memristive Hopfield Neural Network, MHNN)的关联规则算法,主要贡献概括如下:
1)提出改进的MHNN。
MHNN使用忆阻器和电阻组成的分压电阻作为突触,通过开关阵列实现正负突触权值的选择。该网络不仅结构简单,而且能够自适应关联规则挖掘算法的事务矩阵。
2)提出新的基于MHNN的关联规则挖掘算法。
新算法对HNNMFI算法的能量函数、权值以及偏置进行了修改,并设计由最大频繁项集生成关联规则的算法,在软件仿真上能够有效提高关联规则挖掘结果准确度。
1 基本概念
1.1 TEAM模型
TEAM模型对Abdalla等[23]提出的Simmons隧道结模型进行简化,不仅保留Simmons模型准确捕捉阈值的特点和简化Simmons模型的数学表达式,还可通过调整系数以匹配其他忆阻器的数学模型,是一种非常精确且具有潜力的数学模型。该模型的状态变量微分方程、窗函数表达式和忆阻值表达式[5]分别如下:
本文只考虑TEAM模型的忆阻值为线性关系,如式(4)所示。在外部电流正弦信号5sin(2πt)mA的激励下,对TEAM模型按照表1的参数设定进行代码仿真,得到图1的仿真结果。
图1(a)是外部正弦电流信号的波形图,从图1(c)中可以看出,正向电流得到更大电压,验证了TEAM模型的开关变化的非对称性。向该模型中加入图1(d)所示窗函数后,得到了图1(b)所示忆阻值随时间变化的曲线,从图1(b)中可以看出,在电流未达到阈值电流ioff 时,忆阻值保持不变,达到之后忆阻值开始变化。
重新调整TEAM模型的参数,为TEAM模型输入幅值为2V,周期为1s的方波电压,保证此时通过忆阻器的电流大于阈值电流ioff,能够使忆阻值发生改变。从仿真结果中可以得出忆阻值随方波电压连续变化,且成上升趋势,说明方波电压对TEAM模型忆阻器起到阻值编程作用,使TEAM模型忆阻器非常适合作电子突触。
1.2 CHNN基本结构
DHNN和CHNN的区别在于神经元输出不同,前者是二值的网络,神经元的取值为{0,1}或{-1,1},后者的神经元输出在某个区间内连续取值。本文只针对CHNN进行分析,网络中神经元的输入和输出之间呈现sigmoid函数关系[13],该函数的一种常见表达形式[22]如下:
的连接权重;E(v)是能量函数。Hopfield网络解决组合优化问题的步骤为:
1)对于待求解的问题,提供一种合理的解释方案能够使网络的输出表示被求解问题的解。
2)构造能量函数,使能量函数对应被求解问题的目标函数,能量函数向极小值点移动的过程就是问题的求解过程。
3)从能量函数中导出权重Tij和偏置电流Ii。
4)运行Hopfield神经网络,当网络达到稳定状态时的输出就是一定条件下问题的最优解。
1.3 关联规则挖掘基本概念
定义2 支持度。规则XY的支持度为X和Y在D的每个事务中一起出现的概率,记为support(XY)=P(XY)。
定义3 置信度。规则XY的置信度表示为D中包含项集X的事务中项集Y的百分比,即项集Y出现的条件概率,记作confidence(XY)=P(Y|X)。
定义4 频繁项集。若项集X的支持度大等于用户定义的最小支持度,则称X为频繁项集,否则称X为非频繁项集。
定义5 最大频繁项集。如果频繁项集X上的所有超集都不是频繁项集,则称X为局部最大频繁项集,所有局部最大頻繁项集组成的集合称最大频繁项集。
关联规则挖掘算法遵循两个步骤[24]:第一步是找到所有的频繁项集;第二步是在上一步的基础上产生关联规则。考虑到最大频繁项集已经隐含所有频繁项集信息,因此本文只需考虑挖掘最大频繁项集问题。
2 基于HNN的最大频繁项集挖掘算法
2.1 网络结构设计
HNN的神经元分布同事务矩阵D一样,共有n*p个神经元且呈二维数组形式排列。由于每个神经元接收到的突触数量都是一样的,因此该网络可抽象为1行n*p列的单层网络结构。以一个具有2行3列神经元的HNN为例,本文设计的HNN结构如图2所示。
2.2 确定最大频繁项集
本文对Gaber等提出的HNNMFI算法的能量函数进行修改:首先为了同能量函数的标准式对齐,将原能量函数的第二项(偏置部分)前面的符号由加变为减;其次,将第三项中k的累加上限由p改为n。修改后的能量函数能够适用大小不同的事务集,而原能量函数只能适用行数(n)和列数(p)相同的事务集,修改后的能量函数定义如下:
其中:A、B和C是正的常数,代表各个约束项的重要程度,n和p分别代表事务数和项目数,VTi代表第T笔事务中第i个神经元的输出,min是用户定义的最小支持度,bTi表示项目i是否出现在第T笔事务中,是为1,否为0。公式中的前两项确保每行生成一个有效解,该解具有该行表示事务包含的最大项集,第三项确保输出的解是频繁项集,即该解的支持度大于用户定义的最小支持度。
根据图2(a)所示结构,将下标T用A,B代替,重写(6)、(7)和(8)得:
网络参数的选取将会影响网络的效率以及结果准确性,目前对于网络参数的选择尚无理论依据。在实验和经验的基础上,HNN的参数设定如表2所示。
由于网络的迭代次数和步长与事务集所得的权值矩阵有关,使用多个事务集对HNN进行测试后在实验的基础上,总结出网络的权值矩阵同迭代次数Count和步长step的关系如下,其中x是权值矩阵中绝对值最大数的指数。
从能量函数中得到权重和偏置以及确定网络参数后,按照第1章提出的HNN求解组合优化问题的步骤,只需建立并运行HNN,等网络达到稳定状态,便可以求解出最大频繁项集,具体描述如算法1所示。
使用表3所示的事务集对该算法进行测试,minSup和minConf均设置为0.5,网络的迭代次数Count和步长step由式(14)计算后分别为500和10-5,按照算法1流程运行网络,得到编码规则数组code为{beer,bread,cook,diaper,egg,milk},110101,V使用code翻译出来是{beer,bread,diaper,milk},而使用Apriori算法得到的最大频繁项集是{{beer,bread},{beer,diaper},{beer,milk},{diaper,milk}}。可见HNNMFI算法得到的最大频繁项集是定义5中的所有局部最大频繁项集的并集。
3 基于MHNN的最大频繁项集挖掘算法
3.1 电路结构设计
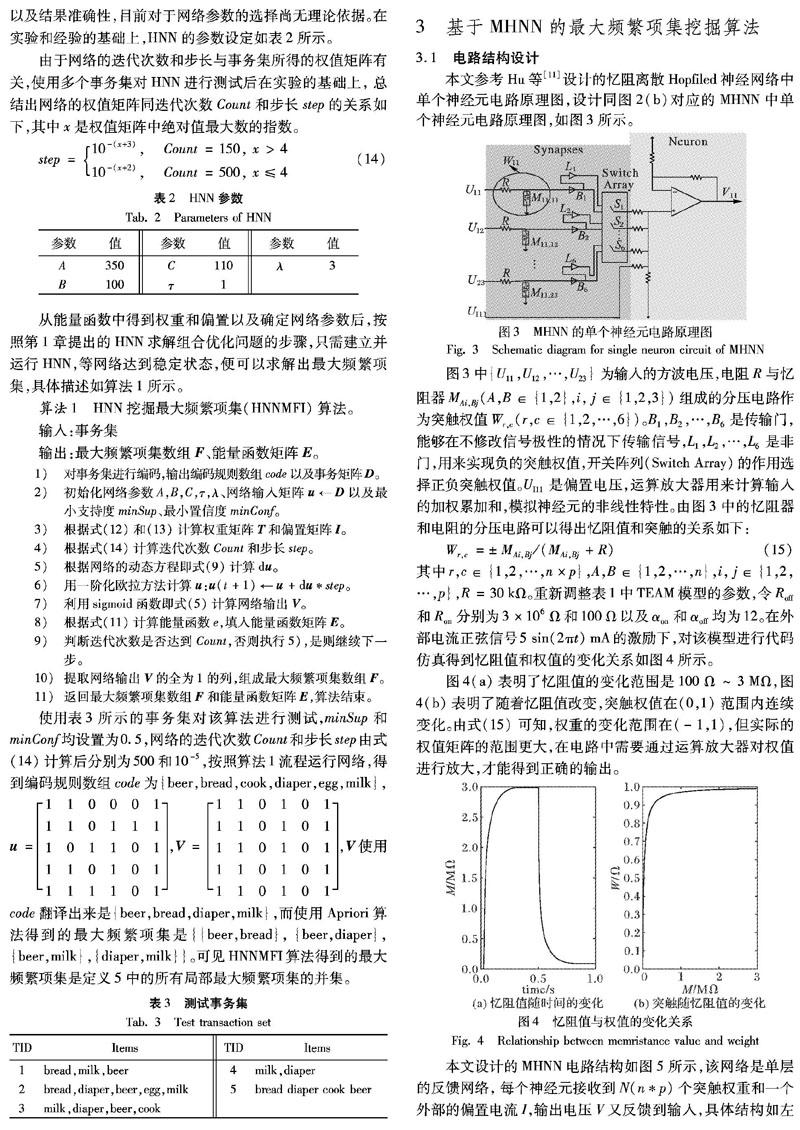
本文参考Hu等[11]设计的忆阻离散Hopfiled神经网络中单个神经元电路原理图,设计同图2(b)对应的MHNN中单个神经元电路原理图,如图3所示。
图4(a)表明了忆阻值的变化范围是100Ω~3MΩ,图4(b)表明了随着忆阻值改变,突触权值在(0,1)范围内连续变化。由式(15) 可知,权重的变化范围在(-1,1)之间,但实际的权值矩阵的范围更大,在电路中需要通过运算放大器对权值进行放大,才能得到正确的输出。
本文设计的MHNN电路结构如图5所示,该网络是单层的反馈网络,每个神经元接收到N(n*p)个突触权重和一个外部的偏置电流I,输出电压V又反馈到输入,具体结构如左边大的最深色阴影部分所示,该部分也是图3的扩展。
3.2 突触权值和偏置的映射
本文的MHNN主要是通过软件仿真实现的,为了对应图5的单个神经元电路,首先将HNN中的权值矩阵Wrc′按照式(16)进行归一化,使归一化之后的权值矩阵范围在(-1,1)之间。
在对权值矩阵进行归一化之后,为了保证MHNN挖掘最大频繁项集算法的结果准确性,还需要将归一化后的权值矩阵按照式(17)进行放大。
4 最大频繁项集生成关联规则算法
本文设计的由最大频繁项集生成关联规则的算法分为两步。第一步生成所有频繁项集的支持度数组,主要通过最大频繁项集的组合运算,产生所有的非空子集(子频繁项集),求出每个子集的支持度,存入支持度数组,具体描述如算法2所示。
第二步从支持度数组中生成满足用户定义的最小支持度与最小置信度的关联规则。首先遍历支持度数组,取频繁项集,作为关联规则XY中的X,再取支持度数组中与X不相交的频繁项集作为关联规则的Y,计算XY的支持度和置信度,满足要求则填入关联规则,具体描述如算法3所示。
5 仿真实验结果分析
5.1 设计生成随机分布事务集算法
由于HNN求解大规模的组合优化问题十分困难,处理小范围的数据集比较容易,所以本文提出的MHNN目前只适用于小规模的事务集,加上关联规则挖掘的测试数据集都比较大,不适用于本文的测试,故本文设计生成随机分布事务集算法来对比两种网络的挖掘结果准确率。该算法具体描述如算法4所示,可通过设置传入事务集的行数n,列数p以及1出现的概率p1来控制随机生成事务集的大小和疏密程度。
5.2 1000次仿真实验的关联规则挖掘结果分析
本文设定算法4的输入n=p,p1=0.5,最小支持度和最小置信度均设置为0.5。设置10种不同大小的事务集,分别为4,6,8,10,12,14,16,18,20,22。對每种事务集分别使用Apriori算法、HNN和MHNN进行100次实验, 以Apriori算法的结果为标准,统计两种网络的挖掘结果准确率,结果如图6所示。
从图6中可以看出,当事务集的大小低于10时,两种网络的挖掘结果准确率相差不大,但随着事务集的增大,两种网络的准确率曲线差距均在0.27以上。通过计算两条曲线差值之和的均值,可得出MHNN在HNN的基础上提升约35.3个百分点的挖掘结果准确率。在上述情况下,又进行多组实验,其中最好结果为36%,最坏结果为33.9%,得出改进后的算法在关联挖掘结果准确率上提高33.9个百分点以上。
6 結语
本文在软件仿真上为忆阻器在HNN处理关联规则挖掘的问题中的应用提出了一种可行的思路。本文设计的MHNN能够处理较小规模的关联规则挖掘问题,但仍然存在容易陷入局部最优点的问题,后续可以考虑使用遗传算法对该网络进行改进。
在硬件实现上,随着关联规则挖掘问题复杂度的增加,需要设计的电路的规模也相应增大,对网络的集成度、能耗以及并行处理能力的要求也越来越高。本文设计的MHNN电路结构可以降低电路设计难度,提高电路自适应关联规则挖掘算法输入的能力,可有效解决传统人工神经网络的瓶颈。
参考文献 (References)
[1] CHUA L O. Memristor—the missing circuit element [J]. IEEE Transactions on Circuit Theory, 1971, 18(5): 507-519.
[2] STRUKOV D B, SNIDER G S, STEWART D R, et al. The missing memristor found [J]. Nature, 2008, 453(7191): 80-83.
[3] DU C, CAI F, ZIDAN M A, et al. Reservoir computing using dynamic memristors for temporal information processing [J]. Nature Communications, 2017, 8: Article No. 2204.
[4] JO S H, CHANG T, EBONG I, et al. Nanoscale memristor device as synapse in neuromorphic systems [J]. Nano Letters, 2010, 10(4): 1297-1301.
[5] KVATINSKY S, FRIEDMAN E G, KOLODNY A, et al. TEAM: ThrEshold Adaptive Memristor model [J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2013, 60(1): 211-221.
[6] 江之源.基于阈值自适应忆阻模型的分析及应用研究[D].重庆:西南大学,2016:11-12.(JIANG Z Y. Analysis and application research based on threshold adaptive memristor model [D].Chongqing: Southwestern University, 2016: 11-12.)
[7] 代祥光.忆阻神经网络的应用[D].重庆:重庆大学,2012:1-3.(DAI X G. Application of memristive neural network [D]. Chongqing: Chongqing University, 2012: 1-3.)
[8] ALIBART F, ZAMANIDOOST E, STRUKOV D B. Pattern classification by memristive crossbar circuits using ex situ and in situ training [J]. Nature Communications, 2013, 4(3): 131-140.
[9] PARK S, SHERI A, KIM J, et al. Neuromorphic speech systems using advanced ReRAM-based synapse [C]// Proceedings of 2013 IEEE International Electron Devices Meeting. Piscataway, NJ: IEEE, 2013: 25.6.1-25.6.4.
[10] ZIEGLER M, SONI R, PATELCZYK T, et al. An electronic version of Pavlov's dog [J]. Advanced Functional Materials, 2012, 22(13): 2744-2749.
[11] HU S G, LIU Y, LIU Z, et al. Associative memory realized by a reconfigurable memristive Hopfield neural network [J]. Nature Communications, 2015, 6: Article number 7522.
[12] HOPFIELD J J. Neural networks and physical systems with emergent collective computational abilities [J]. Proceedings of the National Academy of Sciences of the United States of America, 1982, 79(8): 2554-2558.
[13] HOPFIELD J J, TANK D W. “Neural” computation of decisions in optimization problems [J]. Biological Cybernetics, 1985, 52(3): 141-145.
[14] AGRAWAL R, IMIELINSKI T, SWAMI A N. Mining association rules between sets of items in large databases [C]// Proceedings of the 1993 ACM SIGMOD International Conference on Management of Data. New York: ACM, 1993:207-216.
[15] AGRAWAL R, SRIKANT R. Fast algorithms for mining association rules in large databases [C]// VLDB '94: Proceedings of the 20th International Conference on Very Large Data Bases. San Francisco, CA: Morgan Kaufmann, 1994: 487-499.
[16] 王爱平,王占凤,陶嗣干,等.数据挖掘中常用关联规则挖掘算法[J].计算机技术与发展,2010,20(4):105-108.(WANG A P, WANG Z F, TAO S G, et al. Common algorithms of association rules mining in data mining [J]. Computer Technology and Development, 2010,20(4): 105-108.)
[17] PARK J S, CHEN M S, YU P S. An effective hash-based algorithm for mining association rules [J]. ACM SIGMOD Record, 1995, 24(2): 175-186.
[18] JI C R, DENG Z H. Mining frequent ordered patterns without candidate generation [C]// Proceedings of the 4th IEEE International Conference on Fuzzy Systems and Knowledge Discovery. Piscataway, NJ: IEEE, 2007,1: 402-406.
[19] SAVASERE A, OMIECINSKI E, NAVATHE S B, et al. An efficient algorithm for mining association rules in large databases [C]// VLDB '95: Proceedings of the 21st International Conference on Very Large Data Bases. San Francisco, CA: Morgan Kaufmann, 1995: 432-444.
[20] TOIVONEN H. Sampling large databases for association rules [C]// VLDB '96: Proceedings of the 22th International Conference on Very Large Data Bases. San Francisco, CA: Morgan Kaufmann, 1996: 134-145.
[21] AGRAWAL R, SHAFER J C. Parallel mining of association rules [J]. IEEE Transactions on Knowledge and Data Engineering, 2007, 8(6): 962-969.
[22] GABER K, BAHI J M, EL-GHAZAWI T A. Parallel mining of association rules with a Hopfield type neural network [C]// ICTAI '00: Proceedings of the 12th IEEE International Conference on Tools with Artificial Intelligence. Washington, DC: IEEE Computer Society, 2000: 90-93.
[23] ABDALLA H, PICKETT M D. SPICE modeling of memristors [C]// Proceedings of the 2011 IEEE International Symposium on Circuits and Systems. Piscataway, NJ: IEEE, 2011: 1832-1835.
[24] 徐開勇,龚雪容,成茂才.基于改进Apriori算法的审计日志关联规则挖掘[J].计算机应用,2016,36(7):1847-1851.(XU K Y, GONG X R, CHENG M C. Audit log association rule mining based on improved apriori algorithm [J]. Journal of Computer Applications, 2016, 36(7): 1847-1851.)