基于数学模型对游乐园游玩路线的分析和设计
2019-07-31姜高亮李俊锋
姜高亮,李俊锋
(郑州大学 化工与能源学院,河南 郑州 450001)
近年来,随着中国经济的快速发展,中国额旅游业增长迅猛,许多著名景区人满为患。游乐园作为假期家庭的娱乐休闲场所,其无处不在的新奇、刺激和冒险游乐项目,带给人们无数的快乐和欢笑,吸大多数游客。
1 研究背景
在游乐园中,随处可见大量游客,使得原本项目众多的游乐园变得异常拥挤,与此同时,游客排队等待耗费许多游玩时间,严重影响游园者的体验。在游玩过程中,由于游乐园面积很大,很多游客往往会因为没有规划好合理的路线而玩的不尽兴,这就需要我们制定合理的游玩路线,满足旅游需求,达到游玩更多项目的目的。
2 模型分析
通过游客在迪士尼游玩项目的种类,项目排队时间,项目数量等等因素,可以建立游客游玩最佳体验目标函数,而对于不同游客对同一项目可能有不同的偏好度,可以通过随机偏好度来模拟不同人群,进而分析游客在不同项目游玩的排队时间,建立游客动态游览路线模型,得出仅有一天游玩时间的等待时间最优,游玩项目最优,游玩体验最优的策略。
3 模型假设
1)假设游客一天内最多只游玩某个项目一次。
2)游客在某个项目的游玩时不会早退或逗留更长时间。
3)每个游客对各个游乐项目的偏好度不同,游客对某个项目的偏好度与该项目的排队时间无必然联系。
4)游客在游玩的过程中不会遇到突发情况延误行程。
4 模型的建立与求解
4.1 游客偏好模型的建立
分析建立游客对每个项目的喜好程度,我们可以建立游客偏好与旅游感受值之间的关系。假设游客的数量是m,项目的数量是n,并且游客i对项目j的偏好程度记为pij,pij∈[0,1],pij表明游客i对希望项目j进行游览的目标值,其越大,表面越希望去游玩;则游客i对游乐场内所项目偏好数组记为pij=[pi1,pi2,pi1,…pin]。游客偏好矩阵:
综合游客对各项目的偏好值、各个游玩项目拥挤程度值和旅游感受值的关系,游客i在项目j的旅游感受值为:
(1)
4.2 游玩路线规划模型的建立
基于任何单一行为特征选择目标项目的方式有不能解决游客在景区内分布不均衡的问题,为此李进等人采用了协调控制的方法,投建了协调系数vijh,该系数表示游客i在项目j时选择项目h的可能性,该值综合反映了对游客偏好、项目的拥挤程度和道路阻抗因素的平衡,其值越大说明越能满足游客偏好,项目越不拥挤,道路的阻抗越小[1]。本文沿用该模型,并基于该模型来确定目标项目。
(2)
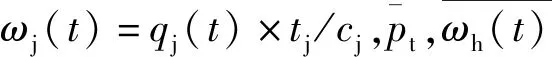
(3)
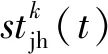
(4)
参数α、β和γ表示模型对游客偏好、项目的拥挤状况和路线阻抗的平衡,三个参数的不同取值代表对三类要素不同的选取。通常α和γ取正值,β取负值,本文沿用文献[3]的研究,α=γ=1,β=-0.3。
4.3 模型检验
我们以上海迪士尼乐园中绳索挑战道、探索步行、胡迪牛仔嘉年华、抱抱龙冲天赛车、晶彩奇航、雷鸣山漂流、风暴来临和冰雪奇缘:欢唱盛会8个游玩项目为例,对模型进行验证和求解。
Step1:生成各个游览项目之间的时间和路径矩阵
由百度地图可定位出入口,选取8个游览项目,由出口到各个项目之间的时间和距离及各个项目的游玩时间和预计排队时间如表1所示。
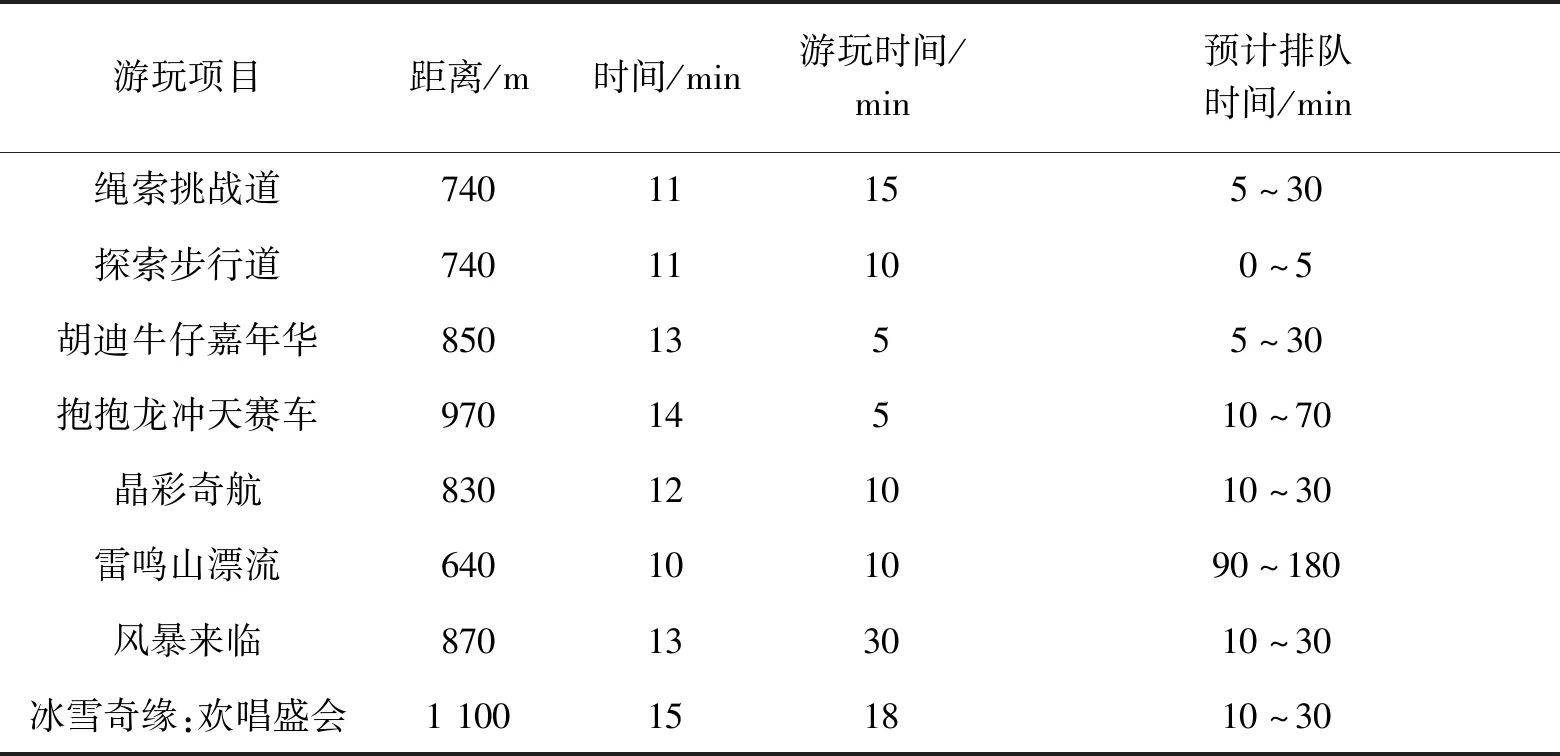
表1 出口到各个项目之间的时间和距离
Step2:生成偏好度矩阵
由于不同游客对游玩项目的偏好度不同,因此本文对这8个游乐项目随机生成了一个1行8列的偏好矩阵pih,以此表示某个游客对这8个项目的偏好程度,实际应用与不同人群时只需将偏好度矩阵修改即可,其中pih∈[0,1],随机生成的偏好程度如表2所示。

表2 不同人群的偏好度
Step3:确定游览项目顺序和路线
由模型假设部分可知,选择下一个游览项目的依据为参数vijh的大小,该值综合反映了对游客偏好、游玩项目的拥挤程度和道路阻抗因素的平衡,其值越大说明越能满足游客偏好,游玩项目越不拥挤,道路的阻抗越小。笔者沿用该模型,并基于该模型来确定目标游玩项目。
将游客游玩的各个项目的具体名称、游玩次序、偏好度、协调系数、到达这一地点的行走时间、排队时间、和游玩时间列表如表3所示,其中协调系数一栏表示的为该时刻从项目j到某一具体的h项目的协调系数值均大于从项目j到其他项目的协调系数值。游玩路线图如图1所示。

表3 游客游玩路线表
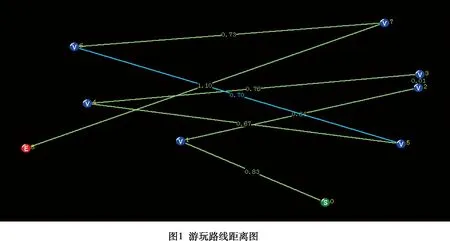
因迪士尼游乐园大部分时间处于游客高峰期,因此所走的路径是适用于高峰期下的Logit模型的路径,时间也是基于这种路径求得。但当游乐园不处于高峰期时,可对路线进行优化。
5 结语
基于Floyd算法求出各点间的最短路径如图1所示,按照走最短路径算出的两个游玩项目之间的行走时间将优于按照现在的路径所走时间,这一行走时间在游客人数未超过园区正常容量的情况下是适用的。
