基于条件期望最大化的断裂航迹粘连∗
2019-07-31赖作镁
赖作镁
(中国电子科技集团公司第十研究所 成都 610036)
1 引言
在非协作目标跟踪过程中,由于未知的目标机动,航迹断裂较为常见[1~4]。航迹断裂将导致航迹连续性差,甚至导致目标数目的误判,这对态势评估及战术决策十分不利。因此,断裂航迹的粘连或关联(Track Segment Association,TSA)技术受到越来越多的关注。Bar-Shalom 首先提出了一种在稀疏传感器分布式系统中处理单目标断裂航迹的方法[6]。在面向预警雷达系统的应用中,文献[5,7]提出了一种将新起批航迹段和已终结航迹段粘连的离散优化方法,两个可能一致的候选航迹首先应该外推到公共时刻,再通过全局约束优化的方法进一步粘连在一起,对航迹的连续性有显著改善。文献[8]提出了一种改进的单点初始化技术,该技术引入了径向速率量测,同时提出了一个更好的有着较小步长的IMM 估计,其适用于采样间隔较长的情况。在面向 GMTI 的应用[9~12]中,考虑到“走-停-走”机动造成的航迹断裂,提出了“双虚拟”的分配方法,通过定义“快状态”和“慢状态”,开发与目标状态相关联的状态转移概率来跟踪机动目标,并进一步利用状态相关模式转移概率的IMM 估计器进行航迹段预测,特别适用于目标机动情形。
引入ESM 属性信息辅助解决MTI 航迹段的粘连,从问题本质来看,它属于状态估计与多参数辨识的联合优化范畴。本文推导出的方案包含通过MTI和ESM 关联的属性指派、在空间和属性约束下的假设优化以及条件期望最大化(ECM)的联合估计与辨识,在此基础上,同时辨识出转弯角速率和机动起始终结时刻。仿真结果表明,该算法可以延长平均航迹维持能力、减少断裂航迹数量、避免不同目标航迹段的误关联。
2 基于ECM的断裂航迹粘连算法
2.1 属性指派
对MTI航迹的属性指派可分为两个步骤:粗关联和细关联。第一步:粗关联,通过如下公式构建距离。
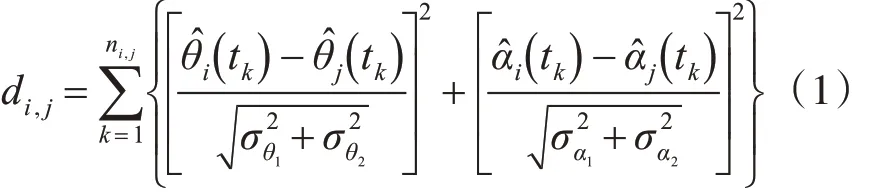
其中,ni,j是第 j 条 MTI 航迹和第 i 条 ESM 航迹状态可能相关的状态数目。ˆ 和分别是 ESM 估计的方位角和俯仰角,ˆ and分别是 MTI 估计的方位角和俯仰角,、分别是MTI 的方位角量测方差和俯仰角量测方差。、分别是ESM方位角量测和俯仰角量测方差。如果第 j 个MTI 航迹可以和第 i 条 ESM 航迹相关联,di,j~χ2( 2ni,j)。如果 di,j≤( 2ni,j),其中 α 为假设检验的预定义显著性水平,第i 条ESM 轨迹与第 j 条MTI 轨迹大致相关。
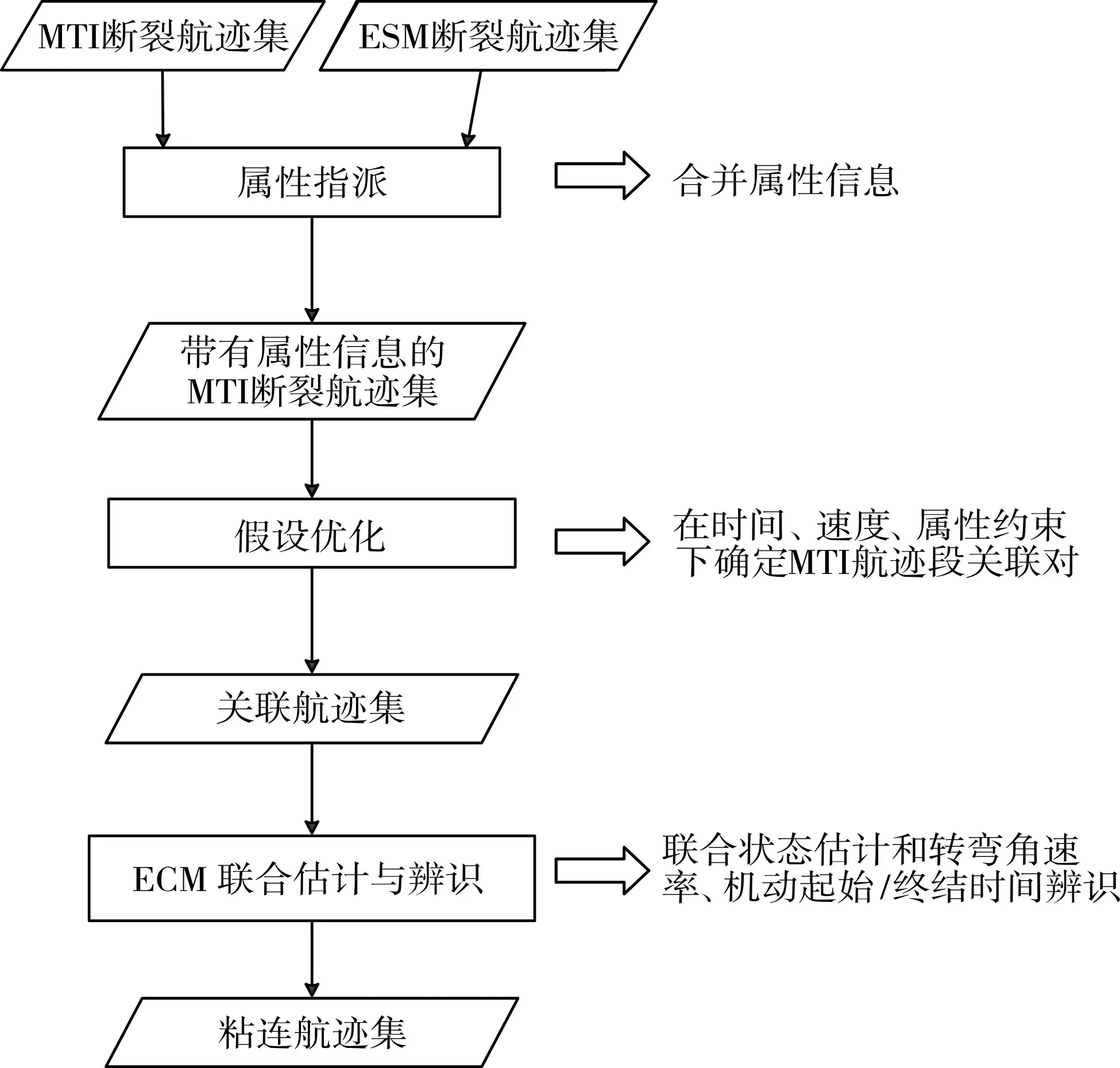
图1 本文提出的TSA算法流程
第二步:细关联。在粗关联之后,如果ESM 航迹与第 j 条MTI航迹大致关联的数目为n(n > 1) 时执行。令:

2.2 假设优化
假设:
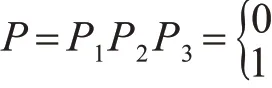
1)时间约束:若 to,e≤ty,s,其中 to,e和 ty,s分别是终结航迹和新起始航迹的终结和起始时间,P1=1,否则 P1=0。
3)属性约束:

若m=n,P3=1,否则 P3=0。若 P=1,两条MTI航迹相关联。
2.3 联合估计与辨识
多个需要识别的参数增加了EM 算法中m 步计算的复杂性,因此采用ECM 算法而不是EM 算法,图2 是基于ECM 算法的联合估计与辨识流程。设i 和 j 表示目标转弯机动的预估起始和终结时刻,Xi:j和Yi:j表示机动过程中的状态和量测。
第1步建模。基于ECM 的TSA算法中,缺失数据是Xi:j被估计的参数是θ=[i , j,ω] 。
第2 步极大似然。完备数据的对数似然函数为


图2 基于ECM的联合优化流程
第3步计算条件期望。计算Q 函数并估计第r次迭代的目标状态。在机动时间[ ]i,j ,得到:

令D(x ,P )=xΤPx ,D(x ,P )=xΤPx 和前者的数目相同,似然函数的条件期望为

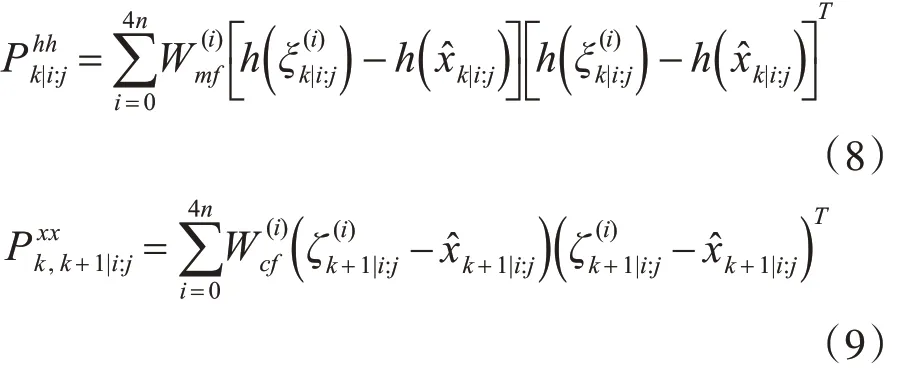
第5 步迭代。重复E 步-CM 步,直到连续两次迭代中的Q 函数值足够接近或迭代次数达到预先设定的上限。
第 6 步 输 出 。 得 到 目 标 状 态 Xˆi:j参 数θˆ=[iˆ,jˆ, ωˆ]的联合估计。
3 仿真结果
假设MTI 的检测概率和漏警率分别为PD=0.90 ,Pf=10-6。MTI 和 ESM 采样周期分别为TM=5s ,TE=1s ,RE=diag{0 .01 rad,0.01 rad} ,RG=diag{5 0m,0.005 rad,0.005 rad,4.5m s} ,目标在 41s~61s 和 101~121s 的机动引起 MTI 航迹断裂,而目标携带的辐射源关机将引起ESM 航迹断裂。这里用航迹连续性指标来表示断裂航迹粘连效果,航迹连续性定义为所有断裂航迹段持续时间的和占航迹总持续时间的比例。目标跟踪模型的详细信息见表1。

表1 目标跟踪使用的参数及算法
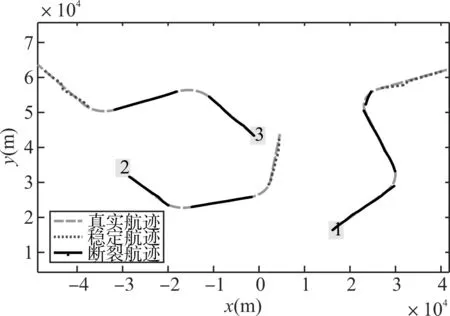
图3 MTI跟踪结果

图4 断裂航迹粘连效果(数字为转弯角速率的辨识效果)

图5 位置估计误差
从图中可以看出所有断裂的航迹全部都被正确粘连,由于空间有限,图5 仅给出了两个目标的粘连精度。3 个目标的断裂航迹粘连精度分别从0.94、0.84、0.69 提高到 0.98、0.98、0.98。仿真结果表明,该方法可以大大改善航迹粘连效果、航迹连续性提升15.7%。
4 结语
提出一种新颖的ESM 辅助下的MTI 转弯机动目标航迹粘连算法,基于ECM 框架实现状态估计、机动起始终结时刻辨识和转弯角速率的联合优化,通过引入ESM 的属性信息避免了来自于不同目标的航迹误关联。仿真结果表明,提出的TSA技术可以减少断裂航迹数量、航迹连续性提升15.7%。
