计及机会维修的电力设备状态检测策略优化模型
2019-07-30徐波张玉敏
徐波,张玉敏
(1. 国网能源研究院有限公司,北京 102209;2.电网智能化调度与控制教育部重点实验室(山东大学),山东 济南 250061)
状态检测是获取设备状态信息的有效手段。设备状态检测间隔过大时,难以及时发现潜在故障隐患,造成设备“欠检修”,带来较大的故障损失;状态检测间隔过小又会造成设备“过检修”,增加检修费用。因此,合理确定设备状态检测间隔对确保电力系统运行的可靠性与经济性至关重要[1-5]。
设备状态检测策略的基本模型是由Barlow等人于1963年首次提出的[6],此后考虑状态检测策略的电力设备检修建模和决策问题逐渐受到关注。文献[7]以电力设备长期运行成本最小为目标,考虑不同劣化状态下检修方式和检修频率对电力设备检修费用和停运损失的影响,对设备检修策略进行优化;文献[8]研究了设备状态转移时间服从一般分布的情况,给出基于半马尔可夫决策过程的求解思路;文献[9]分析了设备可靠性指标随状态检测频率的变化规律,通过优化设备状态检测频率追求设备运行成本的最小化;文献[10]考虑到设备状态检测频率会随着设备劣化程度加剧而加快,基于蒙特卡洛模拟方法求解设备的可靠性指标;文献[11]通过马尔可夫过程描述设备非周期状态检测过程,利用解析法求解设备的可靠性指标,提高了问题求解效率;文献[12]考虑设备可修复故障和不可修复故障,以设备检修、故障、更换等费用最小为目标建立设备状态检测间隔优化模型;文献[13]考虑渐进老化与随机冲击对气体绝缘组合电器设备(gas insulated switchgear,GIS)运行可靠性的影响,综合考虑设备运行可靠性和检修费用,对设备周期性检测频率和检修策略进行优化。上述研究仅就设备个体检修决策展开,没有考虑设备检修与系统运行风险之间的关系。文献[14]推导了变电站负荷可用度、停电频率等可靠性指标,以变电站长期运行成本最小为目标,对设备检测频率、检修频率等进行决策;文献[15]针对设备可靠性参数的不确定性,建立模糊马尔可夫过程优化设备检修策略;文献[16]针对同一输电间隔内的设备,对不同设备状态检测频率和检修方式进行联合优化。
综观现有研究,关于设备状态检测策略的研究未考虑不同故障模式间经济关联,无法量化不同类型故障模式间机会维修策略变动对电力系统风险的影响。由于机会维修能够减少系统检修费用和停运损失,计及机会维修有利于提高设备状态检修的效益。目前,在电力系统检修决策中,机会维修得到广泛应用,如文献[17-19]分别针对电力设备和发电机组建立机会维修模型,显著了提高了系统运行的可靠性和经济性。不足之处在于,上述研究针对电力系统短期检修计划决策展开,无法反映机会维修对系统长期运行成本的影响。
本文针对包含突发性故障和老化故障的电力设备,提出一种计及机会维修的电力设备检测策略优化模型。该模型假设设备状态停留时间服从指数分布,基于马尔可夫过程理论描述设备状态转移过程。在此基础上,对设备不同类型故障模式间经济关联进行量化,给出因经济关联而变动的设备可用度、设备风险和系统运行风险等指标的表达式。然后,分析设备状态检测频率变化对系统长期运行的影响。最后,以系统总风险最小为目标,建立设备状态检测策略优化模型,对设备检测频率和机会维修策略进行优化,并通过算例验证该模型的有效性。
1 计及状态检测和机会维修的设备状态转移过程
在设备老化故障建模中,一般采用多状态马尔可夫过程。图1为设备老化故障状态转移过程。图1中,将设备老化过程划分为4个离散的状态[17],其中D0表示正常状态,D1和D2分别表示注意状态和异常状态,F表示故障状态。设备各状态间转移率为常数λi(i=0,1,2,…),修复率为μf。在设备运行过程中,可以通过状态检测获取设备的状态信息,从而制订设备检修策略,延缓设备故障发展过程。

图1 设备老化故障状态转移过程Fig.1 Transition process of deterioration failure
为计及设备状态检测策略和突发性故障的影响,本文借用文献[11]的建模思想,建立图2所示的设备状态转移过程。图2中,设备老化过程分为正常状态、注意状态和异常状态。其中,正常状态用D0,1表示,注意状态用D1,1和D1,22个子状态表示,异常状态用D2,1、D2,2和D2,33个子状态表示。I0、I1、I2表示设备检测状态,m0、m1、m2、m3表示设备发生突发性故障状态,M1、M2表示设备预防性检修状态,μi表示状态mi对应的修复率,p0、p1、p2分别表示设备从状态M1维修至状态D0,1、D1,2和D2,3的概率,q0、q1、q2分别表示设备从状态M2维修至状态D0,1、D1,2和D2,3的概率,ωi表示状态Mi对应的修复率,γ为检测频率,δ为从检测状态至预防性检修状态的转移率。
研究周期内,对设备进行周期性状态检测,只有经过状态检测或者检修(包括预防性检修、机会维修和故障后检修)后才可以确定设备的实际状态。若经过上一次状态检测或检修后确定设备处于正常状态,在未进行下一次检测或检修前,设备实际状态可能为D0,1、D1,1或D2,1,由于检修人员无法感知设备状态变化,因此会认为设备仍处于正常状态;若经过上一次状态检测或检修后确定设备处于注意状态,在未进行下一次检测或检修前,设备实际状态可能为D1,2或D2,2,由于检修人员无法感知设备是否发生了状态变化,仍会认为设备处于注意状态;若经过上一次状态检测或检修后确定设备处于异常状态,则设备的状态对检修人员而言是确定的,即状态D2,3。

图2 计及机会维修的设备状态转移过程Fig.2 Equipment transition process considering opportunistic maintenance
图2中,当检测到设备处于正常状态时,不需要进行预防性检修;当检测到设备处于注意状态或者异常状态时,进行预防性检修。
设备进入状态mi后,若只进行最小维修,则设备修复至故障前的状态。但是考虑到不同类型故障间存在经济关联,可以在进入状态mi后对设备进行机会维修。也就是说,若在状态mi发现设备处于注意状态或异常状态,则在进行故障后检修的同时对设备进行机会维修。由于设备实际老化状态需要通过状态检测才能确定,因此,当设备进入状态mi后,要增加状态检测(机会检测),各状态具体定义如下:
状态m0:表示设备在状态D0,1发生突发性故障,进行机会检测;
状态m1:表示设备在状态D1,1或状态D1,2发生突发性故障,进行机会检测和机会维修;
状态m2:表示设备在状态D2,1或状态D2,2发生突发性故障,进行机会检测和机会维修;
状态m3:表示设备在状态D2,3发生突发性故障,由于当设备从状态D2,3进入状态m3后,不需要增加状态检测即可确定设备的老化状态,因此在状态m3不需要机会检测即可进行机会维修。
图2中相关参数计算如下:
a)当设备进入状态m0、m1、m2后,由于设备发生故障前的老化状态无法确定,需要增加机会检测,考虑设备机会检测持续时间的影响,可得3种状态的设备修复率分别为:
(1)
(2)
(3)
式中:Δd为实施机会维修所节省的平均时间;μm为突发性故障的修复率。
b)当设备从状态D2,3进入状态m3后,不需要增加机会检测,此时设备修复率
(4)
2 设备可用度表达
本文在进行设备检测策略优化时,决策量为设备检测频率γ和机会维修策略。由于图2给出的设备状态转移过程满足马尔可夫过程,可通过马尔可夫理论求解设备可靠性指标。
令π=[πD0,1πD1,1…πF],其中,矩阵内各元素表示设备处于各状态的稳态概率,则设备稳态状态概率满足[20]
πT=π.
(5)
式中T为设备状态转移矩阵。
式(5)可以写为
π(T-I)=0.
(6)
式中T-I为单位矩阵,可以写为
(7)
式中b0、b1、b2分别为:
(8)
进一步,考虑全概率条件可得
(9)
求解式(9),可得设备α的稳态可用度
Aα=πD0,1+πD1,1+πD1,2+πD2,1+πD2,2+πD2,3.
(10)
3 设备状态检测策略优化模型
3.1 设备风险
设备风险包括检修风险(预防性检修和机会维修)、故障风险和状态检测对应的风险,采用频率和持续时间法求解设备风险。
3.1.1 设备检修风险
设备检修风险是指设备进行预防性检修和机会维修对应的设备个体损失,即
πm3μ3(CP,2-C0).
(11)
式中:EP为设备检修风险;πMi为状态Mi对应的稳态概率;CP,i为设备状态Di对应的预防性检修费用;πmi为状态mi对应的稳态概率;C0为实施机会维修相比单独进行预防性检修所节省的费用。
3.1.2 设备故障风险
设备故障风险是指设备故障引起的个体损失,即
(12)
式中:EF为设备故障风险;CF,M、CF,m分别为设备老化故障、突发性故障对应的检修费用;πD2,i为状态D2,i对应的稳态概率。
3.1.3 设备检测风险
设备检测风险是指进行状态检测引起的设备个体损失,即
(13)
式中:EI为设备检测风险;CI为设备检测费用;πIi为状态Ii对应的稳态概率。
综合上述情况,设备α的风险
Rα=EP+EF+EI.
(14)
3.2 系统运行风险
系统运行风险为系统停电损失费用的期望值,本文根据系统削减负荷损失计算系统运行风险,考虑系统中事故发生概率和引起的损失,系统运行风险
(15)
式中:S为系统故障场景集合;Ls为事故场景s对应的系统负荷削减量(MW/d),本文以天(d)为单位进行计算;Hw为每天包含的小时数,即Hw=24;ce为系统单位失负荷损失;N为系统中的设备数目;N-Ns、Ns分别为故障场景s中处于工作状态、故障状态的设备数目。
3.3 目标函数及约束条件
综合考虑设备风险和系统运行风险,以系统总风险最小为目标,优化设备状态检测频率和机会维修策略,数学模型为
(16)
式中γi为设备i的检测频率,γi,min、γi,max为其下限和上限。
3.4 求解流程
通过遗传算法优化设备检测频率和机会维修策略,模型求解流程如图3所示,遗传算法详细操作步骤参考文献[21],主要包括以下步骤:
a) 初始化染色体种群。种群中每个个体代表系统中各设备的检测频率和机会维修策略。
b)针对种群中每个个体进行染色体解码,得到系统的检修方案,判断其是否满足约束条件。若满足,则计算该个体对应的系统总风险。在设备层,依据设备检测频率和所采取的机会维修策略,建立设备马尔可夫状态转移过程,利用第3.1节中的方法计算设备风险;在系统层,考虑系统负荷需求,求取系统运行风险;最后,将系统总风险作为其适应度值。若不满足,则直接赋予一个较大的数值作为其对应的适应度值。
c)判断算法是否收敛。若收敛,则以适应度最小的个体对应的检修方案作为模型的解;否则,通过染色体之间的交叉、变异、选择,生成下一代种群,返回步骤b)。
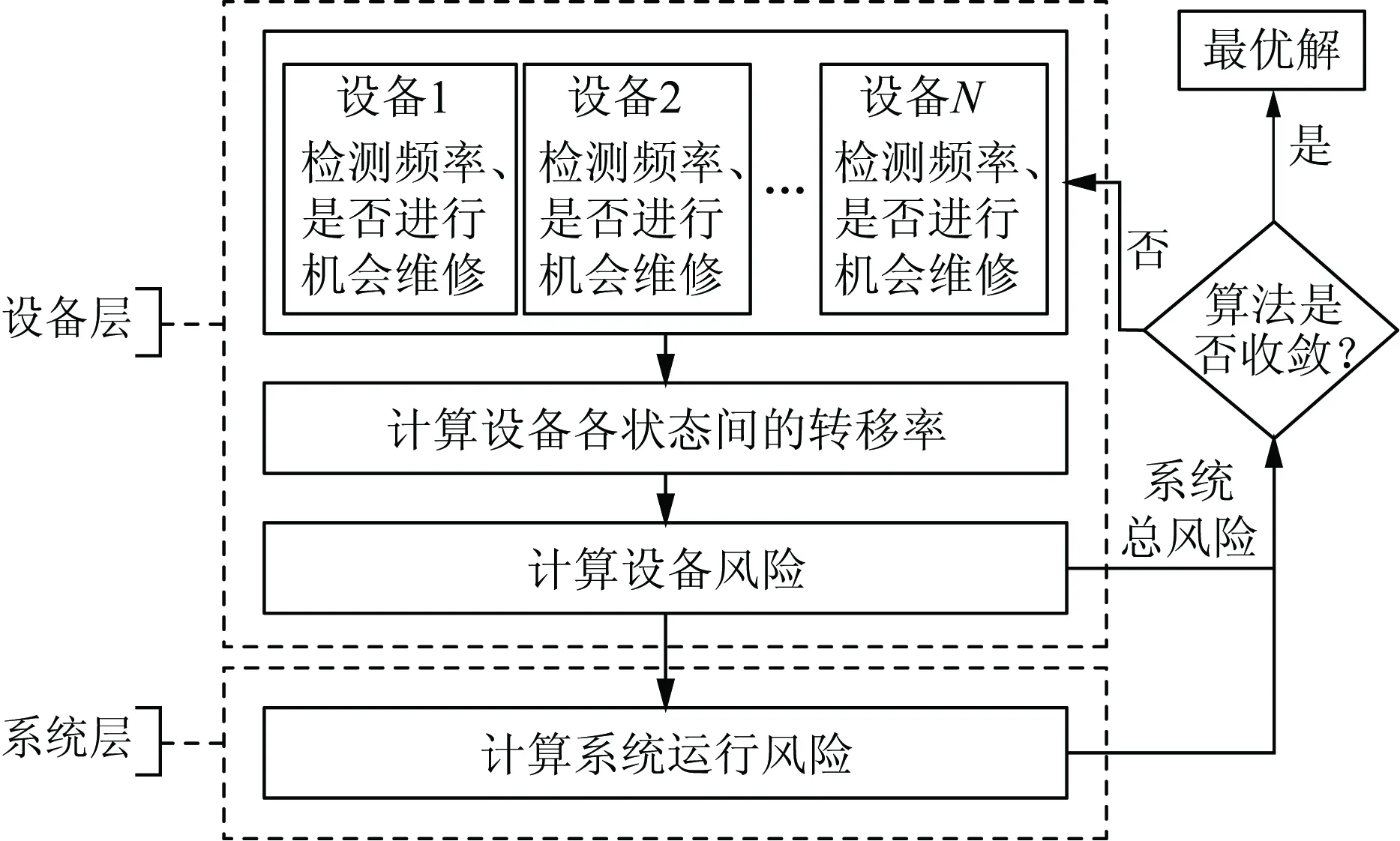
图3 模型求解流程Fig.3 Flowchart of the solution of the proposed model
4 算例分析
本算例对图4所示变电站进行分析,为便于对比,给出了2种典型变电站结构:变电站a和变电站b。以变压器T1为研究对象,变压器检修参数[22]见表1,检修费用见表2。假设其他设备可用度为99.9%,系统负荷为50 MW,单位失负荷损失为10.53元/kWh。

图4 变电站典型结构Fig.4 Typical structure of substation

参数数值λ0/(次·d-1)0.001 19λ1/(次·d-1)0.001 21λ2/(次·d-1)0.002 76λ3/(次·d-1)0.001 00μm/(次·d-1)0.100μf/(次·d-1)0.022ω1/(次·d-1)0.143ω2/(次·d-1)0.070参数数值δ/(次·d-1)10p00.55p10.43p20.02q00.72q10.18q20.10

表2 变压器检修费用Tab.2 Maintenance cost of transformer 万元
4.1 机会维修对检修决策的影响
设定设备不同故障模式间的经济关联参数为C0=2万元,Δd=7 d,分析以下2种检修策略:策略1,不计及机会维修;策略2,计及机会维修。
图5为变压器T1可用度随其状态检测频率变化的曲线。从图5可以看出:①当变压器状态检测频率较低时,变压器可用度随状态检测频率的增加而增大,但当变压器可用度达到最大值后,随着状态检测频率的增加而逐渐降低,变压器从“欠检修”状态过渡到“过检修”状态;②策略2对应的变压器可用度最大,最佳检测频率为0.003 5次/d,这是由于通过机会维修减少了变压器的平均停运时间,提高了变压器可用度。
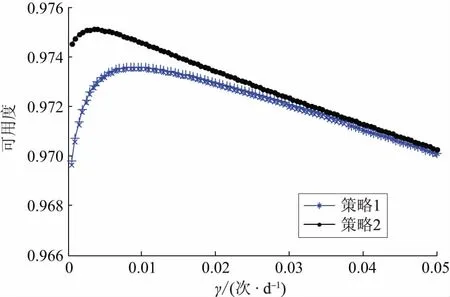
图5 变压器可用度曲线(Δd=7 d)Fig.5 Availability curves of transformer(Δd=7 d)
图6为变压器风险随状态检测频率的变化曲线。从图6可以看出:①当检测频率较低时,变压器风险随状态检测频率的增加而减小;但当变压器风险达到最小值后,随着检测频率的增加而逐渐增加,变压器从“欠检修”状态过渡到“过检修”状态。②策略2对应的变压器风险最小,最佳检测频率为0.001 6次/d,这是由于通过机会维修减少了节省变压器检修费用,减小了变压器对应的风险。

图6 变压器风险曲线Fig.6 Risk curves of transformer
图7为变电站a总风险随检测频率变化的曲线。由于变电站a可靠性较低,变压器T1故障后对变电站运行风险影响较大,如何降低变电站运行风险是检修决策的主要矛盾;因此,变压器可用度最大时对应的变电站总风险最小,最佳检测频率为0.003 5次/d,变电站总风险最小值为32.7。
图8为变电站b总风险随检测频率变化的曲线。由于变电站b中变压器T1故障后对变电站运行风险影响较小,如何降低变压器风险是检修决策的主要矛盾;因此,综合考虑变压器风险和变电站运行风险,变压器T1最佳检测频率为0.002 0次/d,变电站b总风险最小值为0.161。

图7 变电站a总风险曲线Fig.7 Total risk curves of substation a

图8 变电站b总风险曲线Fig.8 Total risk curves of substation b
4.2 经济关联变动对检修决策的影响
令变压器不同故障模式间经济关联有所减小,设定Δd由7 d减小至2 d,图9为变压器T1可用度变化曲线。当不同故障模式间经济关联减弱时,实施机会维修节省的变压器停运时间减少,导致变压器可用度降低,这说明经济关联对变压器可用度有较明显的影响。
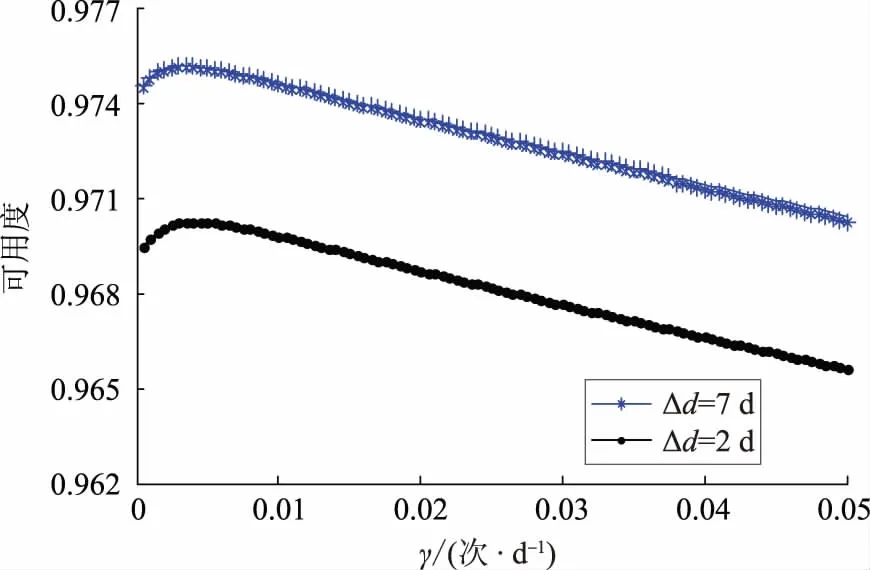
图9 变压器可用度曲线Fig.9 Availability curves of transformer
当经济关联减弱时,以变压器风险和变电站运行风险之和最小为目标进行检修决策,表3为计算结果。
由表3可知:①对于变电站a,由于不同类型故障模式间经济关联减弱,实施机会维修导致变电站总风险增加,策略1对应的变电站总风险最小,变压器最佳检测频率为0.009 0次/d;②对于变电站b,策略1对应的变电站总风险最小,但变压器最佳检测频率为0.003 6次/d,这是由于对变电站b而言,如何降低变压器风险是检修决策的主要矛盾。
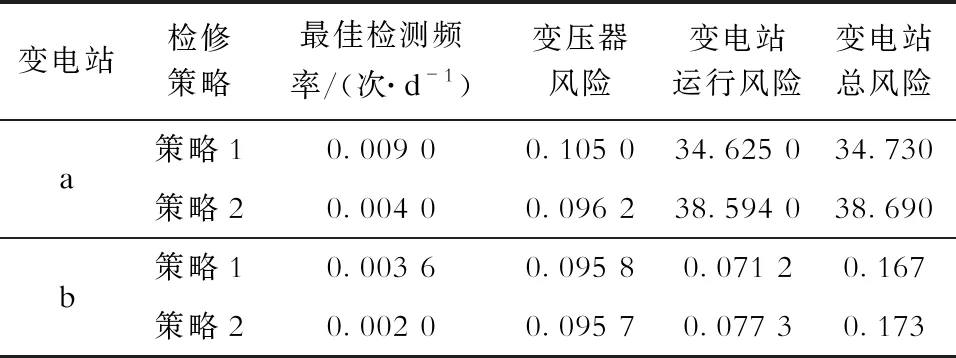
表3 不同检修策略对比Tab.3 Comparison of differentmaintenance strategies
上述算例表明:计及机会维修优化设备状态检测策略是有意义的,不同类型故障模式间经济关联对设备风险和系统运行风险有着重要影响,应该从系统整体角度出发进行检修决策。
5 结论
电力设备运行工况复杂,存在老化故障和突发性故障,为有机统筹设备不同类型故障的检修,本文提出计及机会维修的设备状态检测策略优化模型,经过算例验证,得出如下结论:
a)设备老化故障和突发性故障间存在经济关联,当这种经济关联增强时,实施机会维修有利于提高设备可用度,减小系统运行风险;
b)本文模型能够根据不同类型故障间经济关联对设备性能的影响程度,灵活选择设备检测策略和机会维修策略,有效避免检修不足或者检修过剩,提高系统运行的可靠性和经济性。
