基于样本扩展和特征标记的节假日短期负荷预测

张乔榆，蔡秋娜，刘思捷，闫斌杰，苏炳洪，易江文，杨杉

(1.广东电网有限责任公司电力调度控制中心，广东 广州510600；2.北京清能互联科技有限公司，北京100080)

近年来，随着我国电力市场的不断发展和完善，短期负荷预测面临着前所未有的挑战[1-2]。节假日负荷由于受到外界气象、自身特性和国家调休政策等诸多因素的影响，呈现出固有的不确定性和波动性[3]，如何通过可行的策略和预测方法，挖掘各种相关因素与节假日负荷之间的内在联系，有效提高其预测精度，是当前短期负荷预测的一个研究热点。

负荷预测是通过大量的历史样本数据挖掘其内在的变化规律，从而对其未来态进行估计[4-5]。研究结果表明，节假日与工作日之间的负荷特性存在较大的差异性[6-8]，因此在节假日负荷预测中，考虑工作日的样本策略，未必对预测结果的精度起到积极的作用。在已有的节假日负荷预测研究中，往往只考虑节假日的历史负荷数据，但同类型节假日一年内往往仅出现一次，即使是同一假期，其负荷特性也会随着各年负荷水平的变化而变化[9]，因此当前节假日负荷预测样本策略中容易出现有效样本匮乏的情况。

已有的短期负荷预测研究成果主要集中在算法研究方面，传统方法主要有回归分析法、时间序列法、相似日法、指数平滑法、灰色预测法等[10-14]。针对传统方法中预测精度不高的问题，国内外相关专家和学者做了大量的研究工作，相继提出了一系列新型方法，主要有卡尔曼滤波法[15]、维纳滤波法[16]、BP网络法[17-18]以及支持向量机(support vector machine，SVM)算法[19-21]。各种新型方法的提出不断丰富了负荷预测研究工作；其中滤波算法只考虑负荷自身规律的变化趋势，忽略了外界气象等因素偏差对负荷的影响；BP网络法虽然考虑气象等因素，但也存在泛化能力不强、隐层数目难以确定等缺点；因此这些方法的预测精度和实用性有待考证。相比而言，SVM是一种有监督的学习模型，被广泛用于模式识别、分类及回归分析；且研究表明，应用SVM进行电力系统负荷预测，具有精度高、速度快等优点，对预测效果有较好的改善作用[19-21]。本文基于SVM算法，深入探讨节假日负荷预测问题；然而SVM对样本数据量的要求较高，需要大量的历史样本数据进行训练，才能获得较好的预测结果，而现有的节假日负荷预测样本策略难以满足要求。另外，已有的节假日负荷预测研究中一般只考虑气象等敏感因素，极少涉及到负荷特性，因此如何有效挖掘节假日负荷自身的特征属性也是提高其预测精度亟需解决的一个重要难点。

针对上述问题，本文重点研究非假期的休息日与节假日负荷特性的相似性，提出一种适用于节假日负荷预测的扩展样本策略，并深入探讨所选样本假期类型等特性的标记方式，最后采用SVM方法对其进行预测，以提高预测的准确性。

1 样本扩展策略

1.1 节假日负荷特性分析

我国法定节假日主要有元旦、春节、清明节、劳动节、端午节、中秋节和国庆节，其中春节和国庆节假期一般有7天，其余假期为3天。节假日期间，由于社会生产和人们生活习惯极大不同，与正常的工作日和周休日相比，其负荷特性会表现出明显不同。为了挖掘节假日负荷特性的一般性规律，本文抽取某省份2015—2018年的历史节假日负荷数据，进行分析研究。以2016年历史节假日负荷数据为例绘制负荷曲线，如图1和2所示。

通过分析海量历史数据，发现：

a)在法定节假日，负荷水平显著降低；其中7天长假类型影响范围较广，尤其是春节，波及范围从腊月下旬开始至正月中旬之后；3天小长假类型影响范围相对较小。

b)对于3天小长假来说，负荷往往在法定节假日当天最低；对于国庆7天长假来说，负荷一般在前2天达到最低，而后5天则逐渐开始回升；对于春节7天长假来说，由于假期本身的特殊性，负荷持续较低，且比较平稳。

图1 3天小长假类型Fig.1 3-day small holiday types

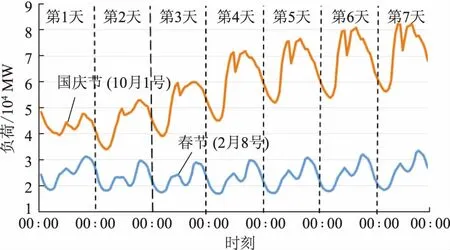
图2 7天长假类型Fig.2 7-day long holiday types

c)3天小长假期间，负荷变化趋势与节日当天在假期中所处的位置有极大关联。若第1天为节日当天，则当日负荷最低，其后2天负荷逐步升高，节假日负荷呈现“/”型变化趋势；若第2天为节日当天，则第2天负荷最低，第1天、第3天相对较高，节假日负荷呈现“V”型变化趋势；若第3天为节日当天，则3天的负荷逐步降低，到第3天时负荷最低，节假日负荷呈现“”型变化趋势。

1.2 休息日与节假日负荷特性相似性分析

通过对海量历史负荷数据的分析可以发现，由于在法定休息日大部分企业会停工、停产或降低生产强度，若不考虑节假日的影响，法定休息日的负荷水平较周一至周五的工作日要低，而且往往在周日达到最低。因此，非节假日的周六、周日、周一这3天的负荷往往也呈现出“V”型变化趋势，与某类3天小长假的负荷特性有一定的相似性。

为了进一步验证休息日与节假日负荷特性的相似性，以某省份2016年劳动节为例进行分析。该节假日期间，法定假日刚好处于第2天，属于典型的“V”型负荷变化趋势，抽取该假期前后近1个月的休息日负荷数据进行对比(如图3—4所示)。

图3 “V”型节假日与休息日的负荷曲线对比Fig.3 Comparison of load curves of “V” typed holidalies and weekends

图4 “V”型节假日与休息日的日最高负荷值对比Fig.4 Comparison of the daily maximum load values of “V” typed holidaies and weekends

由图3—4可以看出，与平常的休息日相比，除了法定节假日当天，负荷减小幅度比较大之外，3天小长假和平常的休息日的负荷特性具有较大的相似度，表现如下：

a)3天内负荷曲线的整体变化趋势比较相似，均呈现为“V”型走向(如图4)；单独对比第1天和第3天，负荷曲线的形状也比较相似。

b)3天内负荷最高峰基本都出现在第3天早晨时段，最低峰则出现在第2天与第3天的交界时段。

c)单独分析每一天，基本都会出现1个早高峰，而低谷则发生在凌晨时段。

1.3 样本扩展

已有的节假日负荷预测方法中，预测样本主要是参考往年的节假日负荷曲线，样本数据缺乏严重影响了预测结果的精度；此外，智能算法在进行模型训练时，需要大量样本来对模型进行训练，才能获得较好的预测结果；因此现有的样本策略难以满足智能算法的需求。

基于节假日与平常休息日的负荷特性较高的相似性，本文提出一种适用于节假日负荷预测的扩展样本策略，在进行样本选择时，不仅考虑了往年历史节假日的负荷数据，还参考了待预测节假日近几年非节假日的周六、周日以及周一的历史数据，可有效提高基础样本的数据量，以满足基于智能算法的预测方法的样本需求。

2 样本特征标记

2.1 节假日特征的标记方式

由第1.1小节的分析结果可知，与正常工作日和周休日相比，节假日会呈现出特有的特征属性，开展节假日特征属性研究，有利于提高其负荷预测的可行性和准确性。对此，针对负荷样本的节假日特征属性(包括节假日种类和负荷变化趋势)，探讨其标记方式，具体如下。

a) 元旦、春节、清明节、劳动节、端午节、中秋节、国庆节的节假日种类特征分别标记为“1”“2”“3”“4”“5”“6”“7”，而非节假日的周六、周日、周一的节假日种类标记为“0”。

b) 对于3天小长假类型，“/”型负荷变化趋势特征分别标记为“1”“2”“3”；“V”型负荷变化趋势特征分别标记为“3”“1”“2”； “”型负荷变化趋势特征分别标记为“3”“2”“1”。

c) 对于7天长假类型，分别标记假期的负荷变化趋势特征为“1”“2”“3”“4”“5”“6”“7”。

d) 对于非节假日的周六、周日、周一样本数据，其负荷变化趋势特征则分别标记为“3”“1”“2”。

2.2 基于特征标记的相关因素矢量

2.2.1 相关因素矢量建立

研究表明，气象信息和季节变化是影响节假日负荷波动的重要因素，综合考虑气象信息和季节变化等因素信息才能进一步提高预测的精度。为此，本文基于上述所提的样本特征标记方式，并结合气象信息和季节变化因素，提出一种基于节假日样本特征标记的相关因素矢量集合，如下：

X={x1,x2,x3,x4,x5,x6,x7}.

(1)

所构建的相关因素矢量重点考虑了7个关键因素，分别对应日最高温度、日降水量、月份、前1天对应时刻负荷、前2天对应时刻负荷、节假日种类以及变化趋势特征，涵盖了气象信息、季节变化、历史负荷数据以及节假日特征等重要因素信息。

2.2.2 归一化处理

在本文所提方法中，以上述所建的相关因素矢量为输入变量，以待预测日的负荷为输出变量。在预测过程中，为了方便处理不同数量级和不同量纲的输入和输出变量，进行归一化处理。本文采用max-min方法进行归一化处理，具体方法如下。

(2)

式中：xi和xi′分别为归一化前后的变量(下标i表示第i个相关矢量)；X为归一化前的输入变量，表示由xi组成的集合；max(X)和min(X)分别为待归一化变量的最大值和最小值。

3 基于样本扩展和特征标记的节假日负荷预测

3.1 SVM基本原理

SVM是基于统计学习理论中的Vapnik-Chervonekis(VC)维理论和结构风险最小化原理而发展起来的，其核心思想是通过内积核函数定义的非线性变换，将输入空间变换到1个高维空间，然后再在该高维空间内建立输入和输出变量之间的线性关系函数，以描述原空间里输入和输出的非线性关系。基本原理叙述如下：

设训练样本集S={(xi,yi),xi∈Rn,yi∈R,i=1,2,…,l}，其中xi为n维的训练样本输入，yi为训练样本输出，l为样本数。对于一般的非线性函数回归问题，SVM常用式(3)来拟合估计：

f(x)=ωφ(x)+b.

(3)

式中：φ(x)为从输入空间到高维特征空间的非线性映射；ω为权值矢量；b为偏置。根据Vapnik的结构风险最小化原理，函数估计问题就是寻找使风险函数式(3)最小的f(x)，即

(4)

式中：C为正规化参数；R为经验风险。

标准SVM一般选用不敏感损失函数ε作为风险函数，即假设所有训练数据在精度ε下用线性函数拟合，这样函数估计问题则可转化为求最小化的优化问题，即

(5)

式中：ξ、ξ*为松弛因子。第1项可使拟合函数更为平坦，从而提高泛化能力；第2项为减小误差；常数C>0表示对超出误差ε的样本的惩罚程度。由此可见这是一个凸二次优化问题，对此可通过引入Lagrange函数对ω和b进行求解，即可求得线性拟合函数

(6)

进一步利用核函数的方法，令

K(x,xi)=ωTω.

(7)

要求解的非线性拟合函数可进一步表示为

(8)

(9)

式中σ2为高斯函数的方差。

综上所述，所对应的SVM优化模型如下：

(10)

3.2 本文方法的计算过程

以上述介绍的SVM为主要工具，并基于样本扩展和特征标记的研究成果，提出一种适用于节假日负荷的预测方法，整体计算流程如图5所示。所提方法的样本策略在传统方法的基础上加入了与节假日负荷特性有相似性的休息日作为样本，以满足SVM对训练样本数量的要求；此外，通过分析节假日负荷特性，提取节假日属性作为样本特征，并建立基于特征标记的相关因素矢量；最后以所建立的相关因素矢量为输入矢量，以待预测日的负荷为输出，并应用智能算法SVM进行训练和预测，从而实现对节假日负荷的准确预测。

在本文所提方法中，分别对待预测日每一时刻的负荷单独进行预测，即在预测待预测日t时刻的负荷时，只采用该时刻点的负荷和气象数据。本文方法的计算过程具体如下。

a)收集研究对象负荷以及气象等历史数据。设定基准日为待预测日的前2天，则收集的历史样本集合为基准日(包含)前2年的样本数据。

b)组建样本扩展集合。从历史样本集合中挑选节假日及休息日对应的样本，组成样本扩展集合以进行模型训练。

c)构建样本扩展集合的相关因素矢量集合X和标签。首先对样本扩展集合中每个样本进行特征提取和标记，并构建其对应的相关因素矢量和标签，其中相关因素矢量涵盖了7个关键因素特征，标签则为待预测时刻负荷；然后对其进行预处理，归一化至[0,1]区间内，以构建样本扩展集合相关因素矢量和标签的归一化形式。

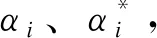
e)预测待预测时刻的负荷。首先，构建并归一化待预测时刻对应的X，并输入到已训练好的SVM模型中，从而得到对应时刻负荷的预测结果；然后对预测结果进行反归一化处理，得到最终的负荷预测结果。

f)对预测结果进行评价分析。针对最终的负荷预测曲线，比对实际负荷数据，采用平均绝对百分误差(mean absolute percentage error，MAPE)指标评价本文所提方法的预测效果。

图5 所提方法的整体计算流程Fig.5 Overall calculation flow chart of the proposed method

4 算例分析

以某省份的全网负荷为研究对象，分别对其2018年元旦、春节、清明节、劳动节及端午节5个节假日负荷进行模拟预测。当对每一个节假日负荷进行预测时，训练的样本扩展集合包括待预测日前2年的休息日及节假日的历史数据，因此本算例中收集了该省份2016年元旦至2018年端午节的负荷及气象数据，形成历史数据库，其中每天数据采集时间间隔为15 min(即每天96个点)。

为了验证本文所提方法的有效性，选取一种传统的节假日负荷预测方法—倍比平滑法，进行预测效果对比。同时，为了便于进行对比分析，选取一种常用的评价指标MAPE，其计算公式如下：

(11)

式中：Yt为待预测日t时刻的预测负荷；yt为t时刻的实际负荷值；T=96，为每天预测的时刻点数。

分别应用本文方法和倍比平滑法对2018年元旦、春节、清明节、劳动节、端午节的日负荷曲线进行模拟预测，预测结果如图6至图11以及表1所示(本文只展示清明和端午假期的预测效果)。

图6 清明假期第1天(2018-04-05)Fig.6 The first day of Qingming Festival(2018-04-05)

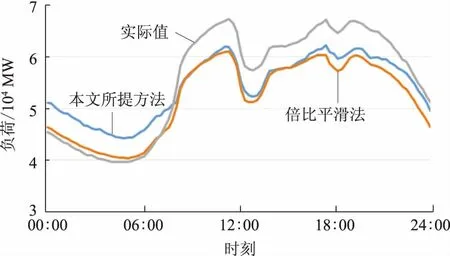
图7 清明假期第2天(2018-04-06)Fig.7 The second day of Qingming Festival(2018-04-06)

图8 清明假期第3天(2018-04-07)Fig.8 The third day of Qingming Festival(2018-04-06)

由图6至图8可以看出，与实际负荷曲线相比，倍比平滑法的预测结果偏差很大，而本文方法则相对较小。这主要是因为传统负荷预测方法中，忽略了负荷样本的节假日属性特征中的变化趋势特征。2017年中清明节处于假期的第3天，而2018年时却为假期的第1天，倍比平滑法在进行负荷预测时，采取了假期顺序对应方式，即预测第1天负荷时仅以往年同类假期第1天作为同类型日，因节假日变化趋势的不同必然导致较差的预测效果。相反地，本文所提方法通过标记节假日的变化趋势特征，并将其作为训练特征输入到SVM模型中，因而具有较高的预测精度。

图9 端午假期第1天(2018-06-16)Fig.9 The first day of Dragon Boat Festival(2018-06-16)

图10 端午假期第2天(2018-06-17)Fig.10 The second day of Dragon Boat Festival(2018-06-17)

图11 端午假期第3天(2018-06-18)Fig.11 The third day of Dragon Boat Festival(2018-06-18)

对比分析图9至图11可以看出，端午假期第1天，2种方法的预测准确率都较高；对于假期其余2天，倍比平滑法预测效果较差，特别是每一天的凌晨和晚上时段，本文方法具有更好的预测效果。

表1为2种方法的预测误差结果对比，其中每个假期的预测误差为整个假期的平均误差，如元旦的预测误差为元旦3天假期的预测误差平均值。由表1可以看出，对于2018年5个假期，倍比平滑法的预测误差平均值高达10.790%，而本文所提方法仅为4.798%；从精度数量级别来看，本文方法提升了1倍多，效果显著；单独对比同一节假日，本文方法的预测误差均远小于倍比平滑法。此外，纵向对比各节假日预测误差，可以发现倍比平滑法在元旦和清明假期的预测误差较大，均超过15%；相比而言，本文所提方法的预测误差较为平均，没有较大波动，具有更好的稳定性。由此可知，本文所提方法更为合理有效。

表1 预测误差对比Tab.1 Comparison of forecasting errors %

5 结束语

本文针对现有的节假日负荷预测精度不高的问题，提出一种基于样本扩展和特征标记的预测方法。首先基于对休息日与节假日负荷特性的相似性分析，在传统样本策略的基础上扩展考虑了休息日，以解决传统方法中样本匮乏问题；其次，基于对节假日负荷特性的分析，提炼其特征属性(节假日种类和负荷变化趋势)，并结合气象等敏感因素建立相关因素矢量；最后，以某省份全网负荷为研究对象进行模拟预测，结果验证了所提方法的准确性和有效性。