双相钢车身板DP780的温热成形本构模型

(山东理工大学 a. 交通与车辆工程学院，b. 机械工程学院，山东 淄博 255049)

随着汽车行业的蓬勃发展，环境与能源问题也日益凸显，全球汽车制造厂商开始积极推动汽车产品朝着低碳、节能、环保和安全等方向不断拓展。先进高强度钢板具有质量小、强度高、成本低等优点，因此广泛用于汽车车身结构件和承重梁，不仅使汽车车身质量得到有效减小，还在很大程度上改善了汽车安全性[1-3]。高强度钢板主要应用于强度要求较高的车身结构，如A柱、B柱、C柱、前后保险杠、车门槛、车身横梁和纵梁、车门侧板等[4]。

温热成形温度是指材料的成形温度低于材料的再结晶温度，其成形温度介于冷成形温度与热成形温度之间，具体材料的成形温度各不相同，并没有统一的界定。与冷成形相比，温成形的成形力小，成形性能好，不需要中间软化的过程，零件的尺寸精度高；与热成形相比，温成形的成形温度较低，氧化、脱碳倾向小，模具寿命长[5-6]。

随着温热成形技术广泛应用于镁铝合金、钛合金等材料冲压成形，部分专家学者开始研究不同温度范围内先进高强度钢板的力学行为及成形性能。文献[5]中通过温拉伸及温胀形实验，建立了先进高强度双相钢DP590的应力-应变模型和温成形韧性破裂准则；文献[6]中基于刚模胀形实验建立了双相钢车身板DP780(DP780钢板)温热状态下的成形极限曲线；文献[7]中通过温拉胀成形得出超高强度钢板Docol 1200M最合适的温拉胀成形温度为400 ℃。虽然上述文献对先进高强度钢温热成形均有一定的研究，但研究温度范围较小，并且没有建立工程应用简单、方便的温热成形本构模型。为了提高双相钢车身板温冲压成形数值模拟的精度，本文中以先进高强度DP780钢板为研究对象，探究DP780钢板温热状态下的力学行为，通过热拉伸实验建立DP780钢板温热成形的本构关系，并对所建立的关系进行实例验证。

1 实验

1.1 材料

本文中单向拉伸实验所用材料为上海宝钢集团有限公司提供的厚度为1 mm的DP780钢板，化学成分如表1[6]所示。

表1 双相钢车身板DP780的化学成分及其质量分数

实验试件取材均由同一板材、方向(沿板材轧制方向)上经激光切割所得，以保证实验材料力学性能的一致性。试件的尺寸根据国家标准GB/T 4338—2006《金属材料 高温拉伸试验方法》规定要求设计，激光切割试样如图1所示。

1.2 方案

实验在CSS-3905型蠕变及持久强度试验机上进行，试验机如图2所示。

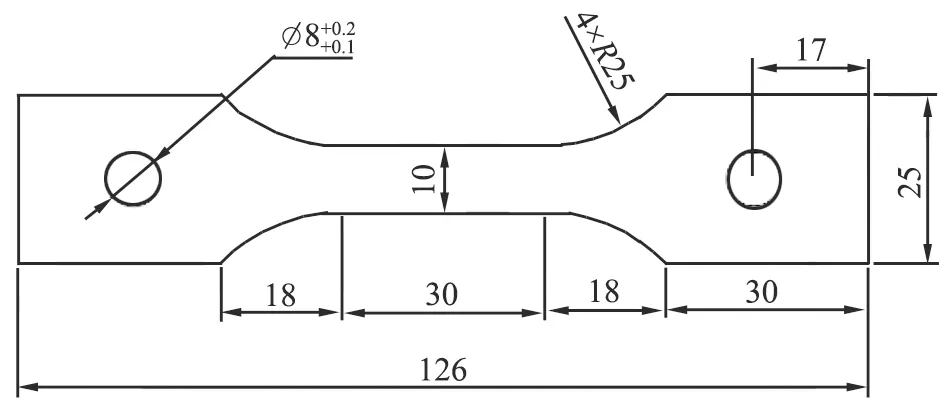
R、∅—圆的半径、直径，mm。图1 双相钢车身板DP780拉伸试件样形状及尺寸(图中单位为mm)

图2 CSS-3905型蠕变及持久强度试验机

实验温度分别为室温(293 K)以及573、673、773、873 K，应变率分别为6.67×10-4、3.33×10-3、6.67×10-3s-1。

实验过程如下：首先将试件加热至实验温度，保温5 min，然后以同一应变率进行等温拉伸，直至试件断裂，采集应力-应变关系数据。图3所示为不同温度、应变率时试件的断裂情况。

图3 不同温度与应变率时的断裂试件图

1.3 结果与分析

实验所得应力-应变曲线为名义应力-应变曲线，需要经过式(1)、(2)转化，获得真实应力-应变曲线，如图4所示。

ε=ln(1+εnom)，

(1)

σ=σnom(1+εnom)，

(2)

式中：ε、εnom分别为拉伸实验真实应变与名义应变；σ、σnom分别为拉伸实验真实应力与名义应力。

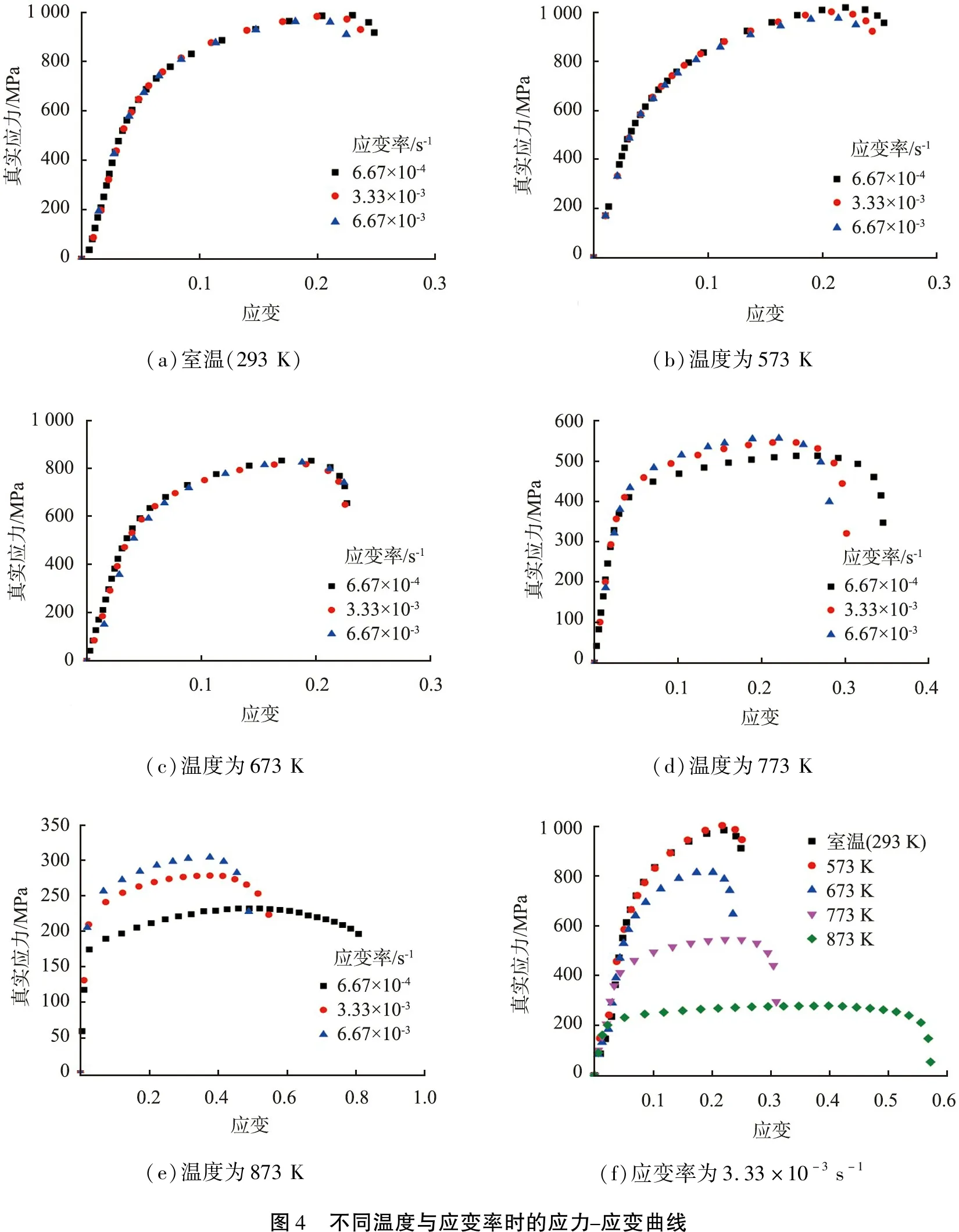
(a)室温(293K)(b)温度为573K(c)温度为673K(d)温度为773K(e)温度为873K(f)应变率为3.33×10-3s-1图4 不同温度与应变率时的应力-应变曲线

根据实验所采集的数据，在温热成形温度范围内，温度比应变率对DP780钢板的弹性模量及屈服强度影响更大。由图4可知，DP780钢板温热拉伸应力-应变曲线与室温条件下应力-应变曲线变化趋势一致，均为一致性较好的拱形曲线。任意温度、应变率条件下，DP780钢板的真实应力随着应变量的增大而增大，属于明显的加工硬化材料。同一温度条件下，当温度低于673 K时，随着应变率的增大，流变应力增大，当温度高于673 K时，随着应变率的增大，真实应力减小；同一应变率时，随着温度的升高，拱形呈宽度变大、高度变小的趋势，说明随着温度的升高，DP780钢板的断后延伸率增大，流变应力逐渐减小，塑性改善。其原因是随着温度的升高，材料自身会产生动态回复，动态回复的机制本质上是位错攀移和重新排列组成较稳定的组态来降低材料变形抗力的多边化过程，并且温度越高，动态回复所造成的软化现象越明显。如图4(f)所示，DP780钢板的屈服强度与抗拉强度相差较大，即相对于其他高强度钢，屈服强度比较小，也说明DP780钢板的塑性变形能力较强，成形性能良好。

为了研究蓝脆现象，进行温度为473 K的拉伸实验。整理应变率为3.33×10-3s-1时，不同温度条件下的真实应力峰值如图5所示。由图可知，随着温度的升高，虽然DP780钢板的塑性显著改善，但是在573 K时会出现蓝脆现象，导致抗拉强度、硬度增大，而延伸率、断面收缩率减小，脆性增大等。如图4(e)所示，当温度为873 K时，随着应变的增大，流变应力先增大后减小，说明在该温度条件下，材料已经达到再结晶温度，产生新的晶粒，增强了软化机制。当动态再结晶与动态回复的软化作用强于加工硬化作用时，曲线开始呈软化趋势。

图5 当应变率为3.33×10-3 s-1时不同温度条件下的真实应力峰值

2 温热本构关系建立与验证

2.1 本构关系理论

本构方程是表征材料变形过程中真实应力与塑性应变、应变率、温度等参数的关系。目前建立本构方程主要有2种方法：一种是基于高温变形实验结果，通过宏观应力-应变曲线，对实验数据进行回归分析，建立合适的流变应力数学模型；另一种是基于变形机理方面的描述，从位错密度、晶粒尺寸等微观结构入手，建立耦合的本构方程[8-9]。

根据近年的研究，目前第1类温热状态的本构模型应用最多的主要有4种，即Johnson-Cook模型[10]、Arrhenius模型[11]、井上胜郎模型[12]，以及Zerilli-Armstrong模型[13]，其中Johnson-Cook模型主要应用于高温、高应变率、大变形条件，Arrhenius方程多用于镁铝合金和钛合金，Zerilli-Armstrong模型中功硬化率与温度和应变率的影响是相互独立的，并不适于描述功硬化率与温度和应变率具有强相关性的材料[14]。相对于以上3种模型，井上胜郎本构模型不仅表述简单、工程应用价值高、适用于高强度钢，而且能够直观描述加工硬化-动态回复型曲线。由此，本文中选用日本学者井上胜郎于1972年提出的井上胜郎本构模型，又称Norton-Hoff模型，其表达式[12]为

(3)

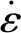
式(3)两边取对数，可得

(4)

2.2 本构模型参数求解

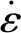
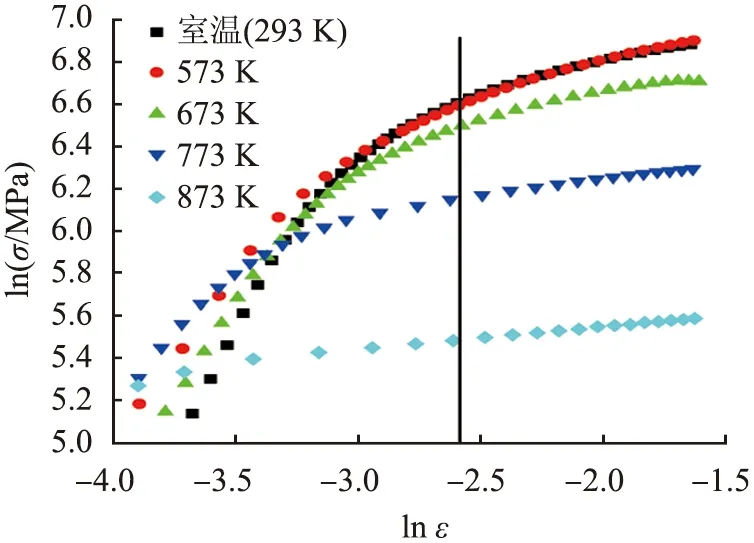
σ—真实应力；ε—真实应变。图6 当应变率为3.33×10-3 s-1时不同温度条件下ln σ与ln ε的关系

表2 不同温度时双相钢车身板DP780的本构模型参数

分别利用线性拟合和二次多项式拟合对n进行修正，结果表明n更适于二次多项式拟合，其相关系数为99.8%，n值二次多项式修正结果为

n=1.403-0.003T+1.375×10-6T2。

(5)

σ—真实应力；应变率。图7 当应变为0.15时ln σ与的关系

当温度低于673 K时，m为负值，真实应力与应变率负相关，并且相关性较小；当温度高于673 K时，m逐渐由负值变为正值，真实应力与应变率正相关，并且温度越高，材料对应变率越敏感。对m二次多项式拟合，结果为

m=0.234-0.001T+2.2×10-6T2。

(6)

继续取应变为0.15且不同温度时的lnσ值，作lnσ与1/T的关系图，拟合直线并求其斜率，可得不同的β值，分别为2 173、1 838、1 718。由文献[12]知，β是与材料有关的常数，因此

β=1/3(1 838+2 173+1 718)=1 910 。

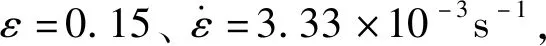
K=0.045T+39.42。

(7)

由此，可得DP780钢板的温热成形加工硬化-动态回复井上胜郎本构模型为

(8)

其中

K=0.045T+39.42 ，

n=0.216+0.001 7T-1.34×10-6T2，

m=0.603 4-0.002 05T+1.712 5×10-6T2。

2.3 模型验证

不同温度时流变应力-应变理论预测值与实验数值对比如图8所示。分别按照式(9)、(10)、(11)求其相对误差δ、标准差S、相关系数r为

(9)

(10)

图8 模型预测值与实验数值对比

(11)

式中：σ′为预测真实应力值；N为有限元模拟组数；Cov(σ′,σ)为预测应力与实验应力的协方差；Var|σ′|、Var|σ|分别为预测应力、实验应力方差。

所求相对误差δ、标准差S、相关系数r如表3所示。由表可以看出，温度为573、673、773、873 K时井上胜郎预测值与实验数据的相关系数分别为99.2%、98.7%、99.2%、98.8%，建立的先进高强度DP780钢板温热拉伸的井上胜郎本构模型的预测值与实验数据吻合较好。

表3 相对误差、标准差、相关系数结果

3 仿真算例

3.1 ABAQUS软件的VUMAT子程序

将建立的井上胜郎本构模型通过FORTRAN语言编写VUMAT子程序嵌入ABAQUS软件中，在ABAQUS软件中设置温度、应变率、材料参数等，实现有限元仿真。VUMAT子程序算法流程如下。

2)按照胡克定律计算试探应力

(12)

3)调用井上胜郎本构模型子程序计算真实应力。

5)若屈服，则计算塑性应变增量Δεp，利用应力补偿更新算法，更新本增量步结束时的应力。

6)更新等效塑性应变与各应变分量

(13)

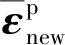
7)结束，返回主程序。

3.2 单向拉伸有限元模型

在ABAQUS软件中建立单向拉伸有限元模型，单元类型为C3D8R，为了保证仿真的准确性，将圆孔处网格单独划分并细化。边界条件与实验条件一致，左端固定，右端施加位移载荷，分别取应变率为3.33×10-3s-1，温度为573、673、773、873 K，结果如图9所示。

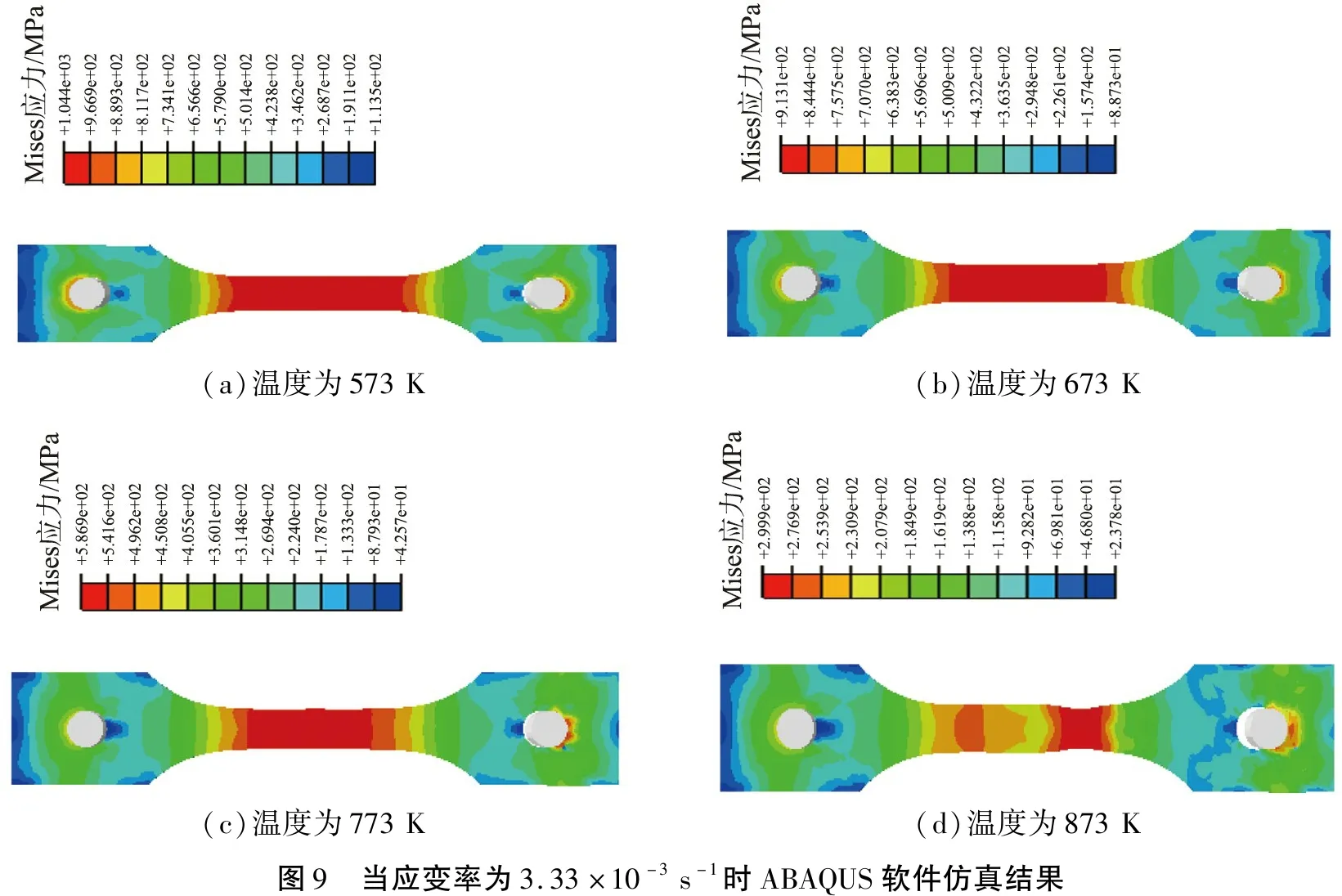
(a)温度为573K(b)温度为673K(c)温度为773K(d)温度为873K图9 当应变率为3.33×10-3s-1时ABAQUS软件仿真结果

3.3 仿真结果分析

分别随机取各温度下模型对称中心右侧某一单元的应力-应变数值、固定点处载荷-位移数值与实验数据对比，结果如图10所示。由图可知，当温度较高时，ABAQUS软件预测值与实验数据吻合较好；温度较低时，预测值与实验值吻合情况相对一般，原因是温度较低并且载荷较小，特别是DP780钢板温拉伸屈服之前，试验机温拉伸载荷、位移数据采集精度有限，这也是材料的弹性模量不能用拉伸试验机直接测得的原因。所建立的井上胜郎本构模型的预测精度在温度高于573 K并且材料进入塑性流动阶段时，完全可以满足先进高强度双相钢温热冲压成形有限元分析的工程需求。

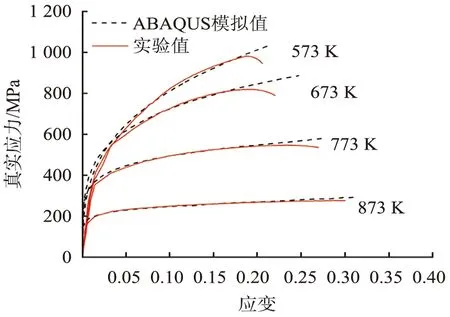
(a)应力-应变曲线

(b)载荷-位移曲线图10 ABAQUS软件仿真与实验对比

4 结论

本文中通过不同温度、应变率的单向拉伸实验，求解并修正了先进高强度DP780钢板的井上胜郎本构参数，并得到以下主要结论：

1)通过单向拉伸实验获取DP780钢板的应力-应变数据，得出其真实应力与温度负相关；当温度低于673 K时，真实应力与应变率负相关，当温度高于673 K时真实应力与应变率正相关；温度为573 K时会出现蓝脆现象。

2)建立的温度场下DP780钢板的井上胜郎本构模型与实验数据吻合较好，相关系数大于98%，可以精确地对先进高强度双相钢简单车身结构件进行温度场下的数值模拟，该模型适合温度范围为573～873 K。