压实度对脱硫石膏动模量和阻尼比的影响试验研究

袁明道卢 博林悦奇

(1.广东省水利水电科学研究院，广州 510610; 2.四川大学 水力学与山区河流开发保护国家重点实验室，成都 610065; 3.四川大学 水利水电学院，成都 610065; 4.中国电建集团 中南勘测设计研究院有限公司，长沙 410014)

1 研究背景

脱硫石膏是燃煤电厂湿法脱硫产生的三大固体废弃物之一，具有产量大、利用率低等特点，目前其综合利用率较低，仍以筑坝堆放处理为主[1]。脱硫石膏筑坝方式与粉煤灰和尾矿等类似，通常采用先建初期坝，而后再分级分期修建子坝方式进行筑坝[2]，由于沉积条件和碾压程度的不同，压实度亦各有差异。近年来，全球地震灾害频发，脱硫石膏作为一种动力敏感材料[3]，合理描述不同压实度下脱硫石膏的动力特性具有重要意义。

参考动应变是求取不同动应变下动模量和阻尼比的关键参数，是动模量和阻尼比函数确定的关键构成。作为一种特殊土体，脱硫石膏的参考动应变与常规土体存在一定差异，合理确定其参考动应变具有重要意义。

自20世纪60年代起，国内外学者对不同类型土体动模量和阻尼比开展了较为深入的研究。1963年，Hardin等[4]给出了砾石土应变幅为10-4时最大动剪切模量Gmax与孔隙比和平均有效主应力关系经验表达式。1984年，Seed等[5]指出砂土动剪切模量Gd分布于一条狭长窄带上，并建立了不同动应变时Gd的经验表达式。Kallioglou等[6]、何昌荣[7]和李瑞山等[8]对黏土动模量进行了研究。唐杰鑫等[9]对滑坡粉质黏土动模量和阻尼比进行了研究。尹光志等[10]对自然固结和机械碾压2种不同压实度下的尾粉砂和尾粉土进行动三轴试验，分析了压实度对2种尾矿动模量和阻尼比的影响。边学成等[11]针对钱塘江粉土动模量和阻尼比特性开展了循环三轴试验研究。周勤等[12]对压实度分别为0.90，0.93，0.95，0.98的黄土动模量和阻尼比进行研究，结果表明随压实度增大，黄土初始动模量逐渐增大，而阻尼比逐渐减小。朱明龙[13]在不同围压和固结比下对石膏进行动三轴试验，指出初始动模量随围压和固结比的增大而增大，阻尼比随围压和固结比增大而减小。综上所述，目前动模量和阻尼比特性研究仍以普通砂土或黏土为主，而压实度对脱硫石膏动模量和阻尼比特性的影响研究有待进一步加强。

本文在等压和偏压2种固结条件下，分别针对某电厂脱硫石膏，进行了不同压实度下的动三轴试验，研究了压实度对脱硫石膏动模量和阻尼比特性的影响，建立了考虑压实度的脱硫石膏初始动模量计算公式，进而推求了考虑压实度的动模量衰减全过程曲线，并给出了脱硫石膏参考动应变取值范围。

2 试 验

2.1 试验仪器

试验仪器为单向振动三轴仪，仪器主要由主机、测控系统和传感器等构成，如图1所示。其中:主机为DZ78-1型电磁式动三轴仪；测控系统为DDS-70动三轴测试系统；力传感器型号为BLR-1;孔压传感器型号为AK-1(量程0～1 MPa);位移传感器为DA-2(量程±2 mm)。通过对仪器进行改进并尽可能减少活塞摩擦，自制应变计拾取的信号经动态电阻应变仪和X-Y函数仪两级放大后，竖向变形测量精度达10-4mm级，可较准确地量测到轴向动应变εd= 10-6级。

2.2 试验土料

试验土料为某电厂脱硫石膏，颜色为灰白色，相对密度为Gs=2.53，通过粒度分析仪平行2次测定，2次测定的土样分别编号为G1和G2，取2次测定结果平均值为试验结果。脱硫石膏级配如图2所示，砂粒(1～0.075 mm)占6.92%，粉粒(0.075～0.005 mm)占82.84%，黏粒(≤0.005 mm)占10.24%，液限wL=29.6%，塑性指数IP=7.5，可分类定名为低液限粉土ML[14]。通过轻型击实试验确定最大干密度ρdmax=1.56 g/cm3，最优含水率wop=19.4%。

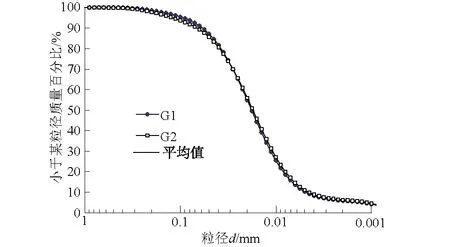
图2 脱硫石膏级配Fig.2 Gradation of desulphurized gypsum

2.3 试验程序

根据现场调研及室内常规土工试验结果拟定3个压实度R(0.85，0.90，0.95)，确定制样干密度和含水率。试样直径Φ=50 mm，高H=115 mm，采用湿捣法分5层制备，精确称取每层土样质量，并保持每层击实高度一致，对每层脱硫石膏接触面进行刮毛处理以保证上下土层接触良好。试样采用真空抽气饱和法进行饱和，饱和及试样用水均采用蒸馏水。试样饱和后，缓慢打开排水阀，对试样进行双面排水固结，固结方式分等压和偏压固结2组：等压固结，固结比Kc=1，围压σ3=100，200，400 kPa；偏压固结，围压σ3=100 kPa，固结比Kc=1.0，1.5，2.0。固结稳定后测记排水量，固结稳定标准为关闭排水阀5 min后，孔隙水压力不再上升。固结完成后施加循环动荷载，荷载波形为正弦波，振动频率1 Hz。每一围压或固结比按等差方式从小到大依次施加30级振动荷载，每级荷载振动2周[15]。

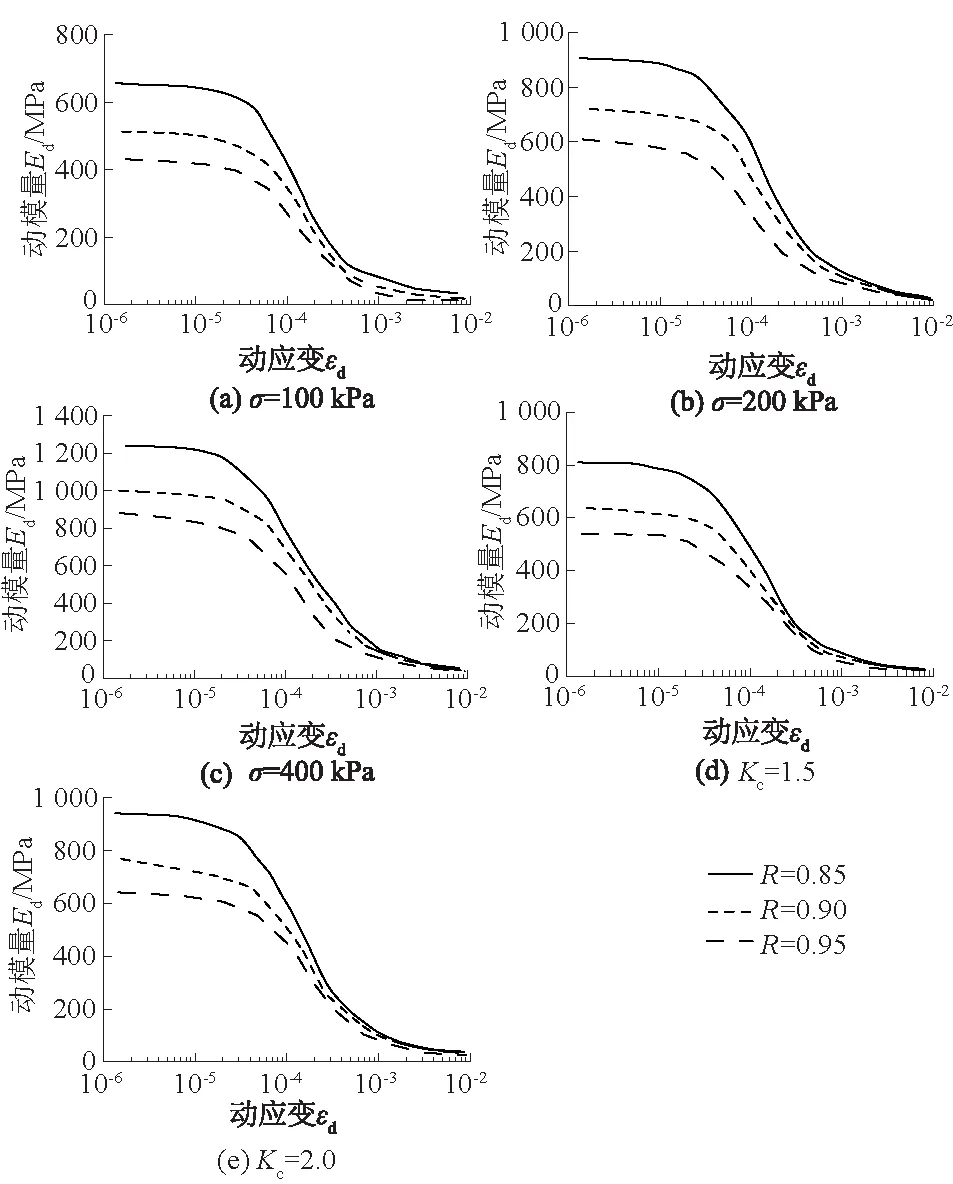
图3 不同压实度下脱硫石膏Ed-εd关系曲线Fig.3 Curves of dynamic modulus Ed versus dynamicstrain εd of desulphurized gypsum with varied compactness

3 试验结果与分析

3.1 动模量

3.1.1压实度的影响

不同压实度下石膏的动模量Ed与动应变εd关系曲线如图3所示。可知：随压实度增大，不同固结方式脱硫石膏土样同一动应变εd对应的动模量Ed均逐渐增大。分析其原因为动荷载作用下，脱硫石膏骨架会受到一定的惯性力与干扰力，由于土颗粒质量、排列方式和初始应力条件等方面的差异，其作用于各个土颗粒上的力在大小、方向以及产生的实际影响等方面会有明显不同，进而在土颗粒接触点产生新的应力[16]。当该应力超过一定值时，会破坏土颗粒间原有的联结强度与结构状态，使颗粒彼此间脱离接触。脱硫石膏压实度越大，土样越紧密，土颗粒间作用力越强，颗粒原有联结骨架越不容易破坏，颗粒越难以彼此脱离，土样抵抗变形能力越强。

3.1.2 考虑压实度的初始动模量

取动应变εd=10-4～10-2范围的动模量Ed，将1/Ed～εd试验点线性拟合并延长，其与纵坐标εd=0交点的倒数即为初始动模量Ed0[7]。不同σ3和Kc下初始动模量Ed0与压实度R关系曲线如图4所示。可知，随R增大，不同σ3和Kc下Ed0均增大，且具有良好的幂函数相关性。何昌荣[7]考虑σ3和Kc的影响，建立Ed0的估算经验公式,即

Ed0=K1pa(σ3/pa)n(Kc)m。

(1)

式中：K1，n，m为试验参数；pa为标准大气压。

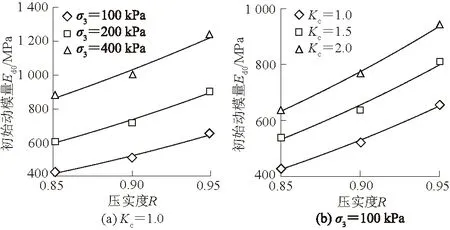
图4 初始动模量Ed0与压实度R关系曲线Fig.4 Curves of initial dynamic modulus Ed0 versuscompactness R

压实度R越大，脱硫石膏越紧密，结构越稳定，越难以发生变形，Ed0越大。考虑压实度R的影响，式(1)可改写为

(2)

式中：K1为反映土性影响的参数；n为反映围压影响的参数；m为反映固结比影响的参数；s为反映压实度影响的参数。试验参数物理意义明晰。经试验验证不同类型土体(黏性土、砂性土、原状土和扰动土)参数n均为0.5左右[7, 17-19]，则式(2)可写为

(3)

式中拟合参数K1=7.9×106，m=0.55，s=3.95。

将等压和偏压固结下采用式(3)计算所得的脱硫石膏Ed0与试验所得的Ed0分别列于表1和表2。计算结果与试验结果误差均在±5%以内，说明建立的考虑压实度的初始动模量计算公式是合理的。

表1 等压固结下脱硫石膏初始动模量Table 1 Initial dynamic modulus of desulphurized gypsum under isotropic consolidation

表2 偏压固结下脱硫石膏初始动模量Table 2 Initial dynamic modulus of desulphurized gypsum under anisotropic consolidation

3.1.3 动模量衰减模型

采用Ed/Ed0对不同Kc，σ3，R下脱硫石膏动模量进行归一化处理，不同Kc，σ3，R下脱硫石膏Ed/Ed0-εd关系曲线如图5所示。可知：不同Kc，σ3和R下脱硫石膏Ed/Ed0-εd试验点基本集中于一条狭长带上，随εd增大，Ed/Ed0逐渐减小；εd<10-5时，Ed/Ed0变化不明显，εd=10-5～10-3时，随εd增大，Ed/Ed0显著减小，εd>10-3时，Ed/Ed0变化逐渐趋于平缓。Ed/Ed0随εd衰减过程可由双曲线函数描述[20],即

(4)

式中εr为参考动应变，为破坏动剪应力τm与Ed0比值。拟合试验点εr=1.8×10-4，试验点上包线εr=4×10-4，下包线εr=1×10-4；初步确定脱硫石膏εr取值范围为1×10-4～4×10-4。

将式(3)代入式(4)有

式(5)为脱硫石膏动模量Ed衰减全过程曲线，通过式(5)可获得不同Kc，σ3，R下每一εd对应的Ed。

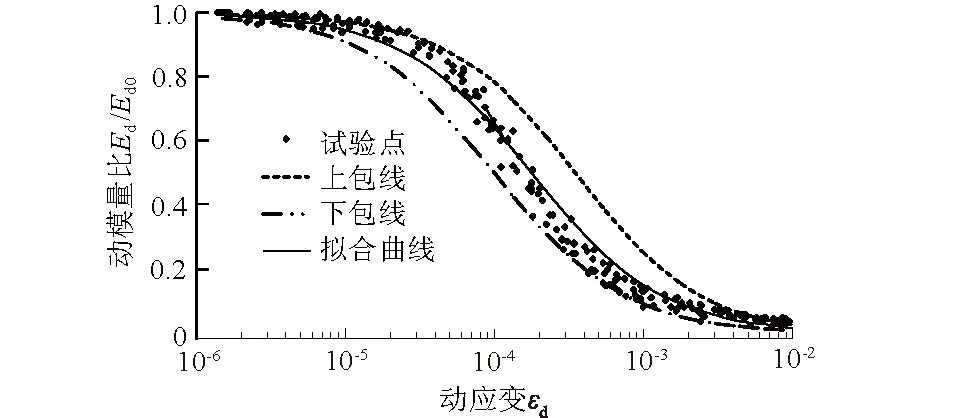
图5 Ed/Ed0-εd关系曲线Fig.5 Curves of Ed/Ed0 versus εd

3.2 阻尼比

不同压实度下石膏的阻尼比D与动应变εd关系曲线如图6所示。可知：εd>10-5时，随压实度R增大，同一应变εd对应的脱硫石膏阻尼比D逐渐减小，这是由于压实度越大，脱硫石膏颗粒间接触越紧密，土样刚度越大，循环荷载作用下能量损耗越小；εd<10-5时，不同R下脱硫石膏D相差较小，分析其原因为εd较小时，脱硫石膏主要处于弹性阶段，循环荷载作用下不同R的脱硫石膏能量损耗差异小；R相同时，D随Kc和σ3增大而逐渐减小。

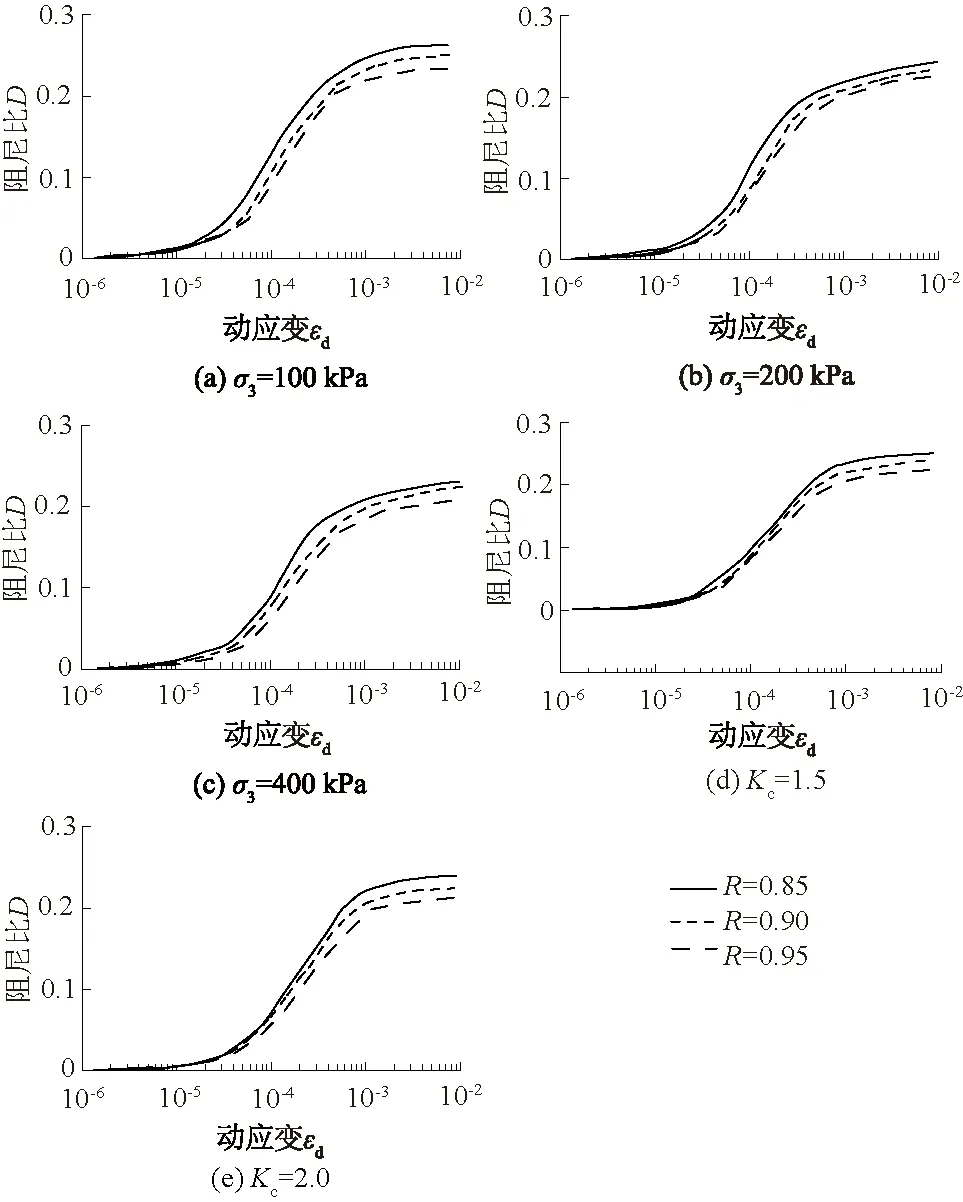
图6 不同压实度下脱硫石膏D-εd关系曲线Fig.6 Curves of damping ratio D versus εd ofdesulphurized gypsum with varied compactness

取脱硫石膏D-εd曲线右渐近常数为最大阻尼比Dmax，经D/Dmax归一化后，不同Kc，σ3，R下脱硫石膏D/Dmax-εd关系曲线具有相同特征，试验点密集于较窄的条带内，如图7所示。可知D随εd的变化规律与Ed随εd的变化规律相反：εd<10-5时，D/Dmax变化不明显；εd=10-5～10-3时，随εd增大，D/Dmax显著增大；εd>10-3时，D/Dmax变化逐渐趋于平缓；D/Dmax随εd变化过程可描述为

(6)

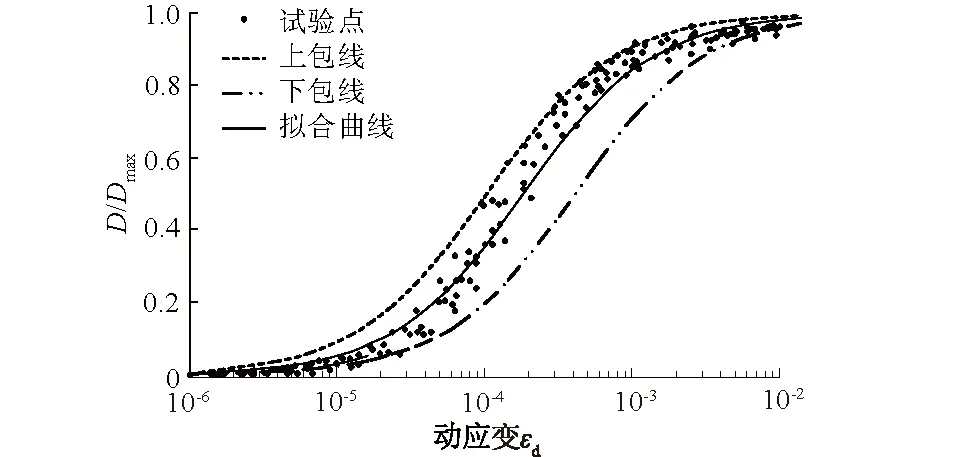
图7 D/Dmax-εd关系曲线Fig.7 Curves of D/Dmax versus εd

拟合试验点εr=1.8×10-4，试验点上包线εr=4×10-4，下包线εr=1×10-4；进一步验证了脱硫石膏εr取值范围为1×10-4～4×10-4。

3.3 试验结果转换

3.3.1 动模量与动剪切模量转换

根据材料弹性理论，动应变εd与动剪应变γd转换关系式为

γd=εd(1+μ) 。

(7)

式中μ为泊松比。

动剪应力τd与动应力σd关系式为

(8)

动模量Ed和与动剪切模量Gd关系式为

(9)

Ed和Gd可相互转换，Ed-εd关系与Gd-γd关系具有相同规律，故考虑压实度影响的初始动剪切模量Gd0可写为

(10)

考虑压实度影响的动剪切模量Gd可写为

(11)

式中γr为参考动剪应变。

3.3.2 动模量与阻尼比转换

将式(4)代入式(6)有

(12)

由于Ed-εd关系与Gd-γd关系具有相同规律，故式(12)可进一步改写为

(13)

Hardin等[20]根据应力-应变滞回圈几何特征推导得到了与式(13)一致的转换公式。通过该式可直接对脱硫石膏D/Dmax，Ed/Ed0，Gd/Gd0进行转换。

4 结 论

在等压固结和偏压固结条件下，分别对压实度为0.85，0.90，0.95的3组脱硫石膏试样进行振动三轴试验，分析了压实度对脱硫石膏动模量和阻尼比的影响，主要结论如下：

(1)随压实度增大，脱硫石膏动模量逐渐增大;阻尼比在动应变<10-5时差异不明显，动应变>10-5时逐渐减小。

(2)在试验压实度范围内，脱硫石膏初始动模量与压实度具有良好的幂函数相关性，基于何昌荣提出的初始动模量估算经验公式，建立考虑压实度影响的初始动模量计算公式，其计算结果与试验结果吻合良好。

(3)不同压实度下，归一化脱硫石膏动模量和阻尼比试验点均密集于较窄的条带内，试验用脱硫石膏参考动应变取值范围为1×10-4～4×10-4。