水下机械手分数阶积分滑模轨迹跟踪控制方法研究
2019-07-29黄道敏韩丽君唐国元周曾成徐国华
黄道敏 韩丽君 唐国元 周曾成 徐国华
1.华中科技大学船舶与海洋工程学院,武汉,4300742.空军预警学院预警技术系,武汉,430010
0 引言
海洋研究领域的逐步扩展,对水下自主航行器(autonomous underwater vehicle, AUV)的续航及作业能力提出了更高要求,这往往需要利用水下固定或移动平台对AUV进行捕获和对接,从而进行能源补充及数据交互。在固定或移动平台上安装水下机械手来实现对运动状态下AUV的捕获及对接作业是其中的重要方式之一。
考虑机械臂搭载于固定式平台捕捉水下航行器的情况,可将该系统的水下捕获对接过程简化为具有固定基座的水下机械手末端执行器对航行器的轨迹跟踪问题。目前提出的控制方法很多,包括PID控制[1]、自适应控制[2]、滑模控制(SMC)[3]、反演控制[4]、模糊理论[5]和神经网络控制[6]等,还包括采用以上两种及两种以上的混合控制技术。其中,滑模控制因具有操作简单、响应速度快、对系统的不确定性不敏感等特点而被广泛采用。滑模面的选择和控制律的设计是决定滑模控制性能的两个关键因素。文献[7-9]采用了线性类型的滑模面,如PID型滑模面,其中文献 [7]对趋近律函数进行了改进。文献[10-11]采用了非线性类型的滑模面,如终端滑模面,且文献[10]设计了一种新的分层终端滑模面。由于线性滑模面是关于误差及其导数或积分项的线性函数,因此只能实现渐近收敛。有些终端滑模控制方法虽然能够保证在有限时间内收敛,但是仍然需要考虑存在的奇异性问题,文献[12-13] 通过修改终端滑动面来解决奇异性问题。
本文采用分数阶理论,设计了一种基于指数趋近律的分数阶积分滑模控制方法,避免了奇异性问题。由李雅普诺夫理论的分析可知,该控制方法可以保证系统的渐近稳定性。通过对六自由度水下机械手对运动目标的轨迹跟踪控制的数值仿真,验证了所提控制方法的有效性和鲁棒性。
1 机械手的动力学模型
1.1 问题描述
机械手对运动目标的轨迹跟踪见图1。背部安装有导杆的航行器在确定的XY平面自主航行,其航行路线处于机械手末端执行器的工作空间范围内时,机械手控制系统可以通过传感器(如双目视觉)获得目标导杆的精确位置和姿态信息,并将其作为此时机械手末端执行器的目标信息。控制系统将机械手实际的位置和姿态信息与目标信息进行比较,并将两者的误差在控制器中进行计算, 然后输出相应的关节控制力矩来实时调整机械臂的各个关节角度。经过一段时间,机械手末端执行手爪最终能够捕获安装在航行器上的目标导杆。
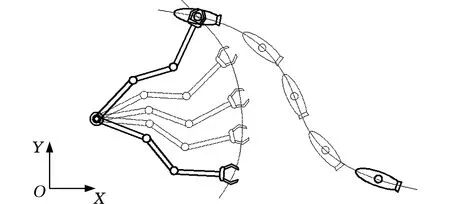
图1 机械手对运动目标的轨迹跟踪示意图Fig.1 The diagram for a manipulator to track a moving target
1.2 动力学方程
本文所采用的六自由度水下机械手构型见图2。使用D-H方法描述该结构[14],为每一个连杆分别定义4个量,包括连杆扭角αi-1、连杆长度ai-1、两连杆距离di、两连杆夹角θi(i=1,2,…,6)。所建立的机械手坐标系见图3,相应的连杆参数见表1。

图2 机械手构型Fig.2 The configuration of the manipulator
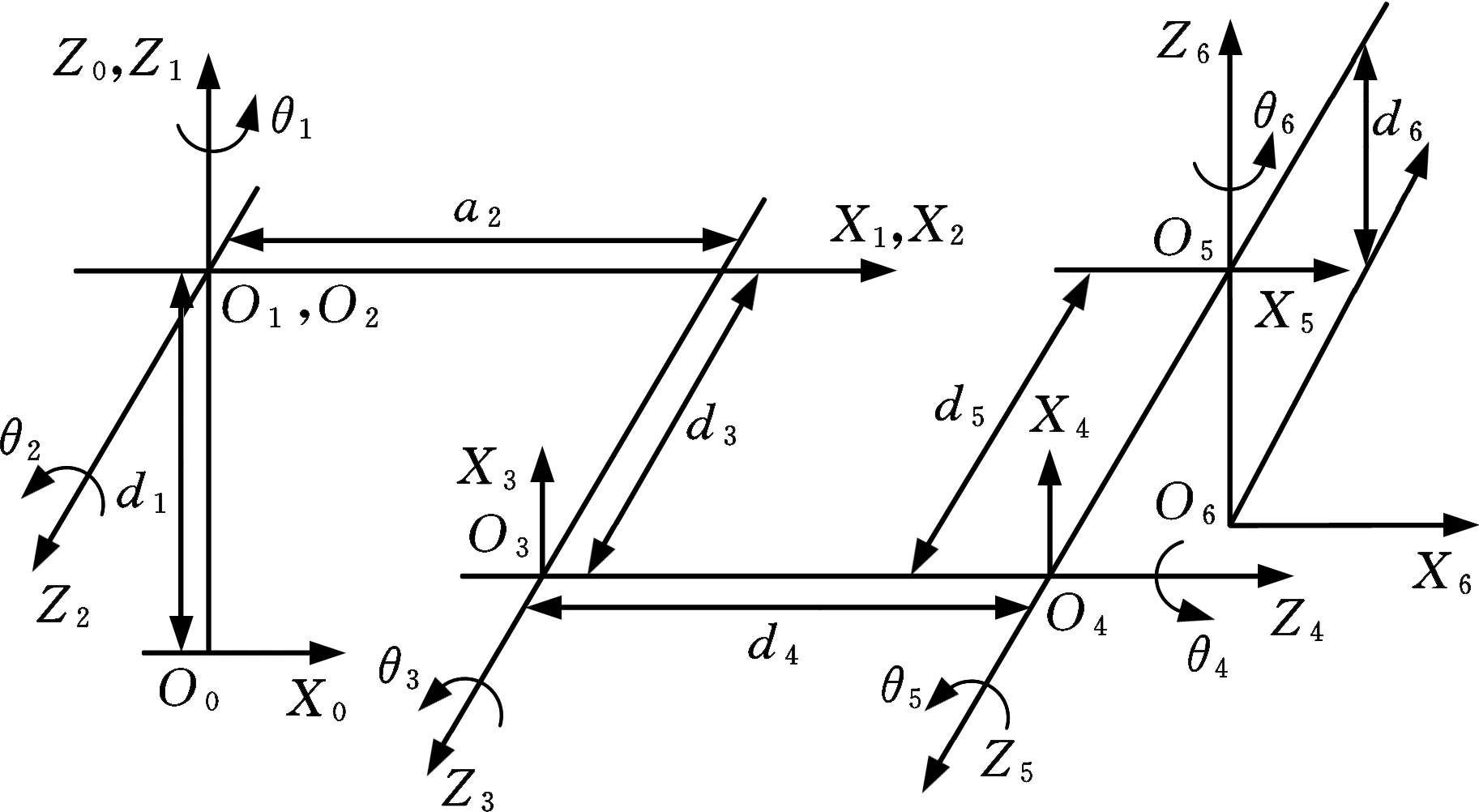
图3 连杆坐标系Fig.3 The frame of the manipulator表1 六自由度机械手连杆参数Tab.1 The link parameters of the 6DOF manipulator

连杆i扭角αi-1(°)长度ai-1(m)偏移di(m)角度θi(°)100d1θ129000θ230a2d3θ34900d4θ45-900d5θ56-900d6θ6
六自由度水下机械手的动力学方程表示为
(1)
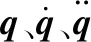
式(1)具有如下特性:
M(q)=(M(q))Τ
|M(q)|>0
为了简化式(1),定义
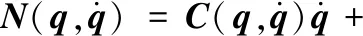
则由式(1)可得
(2)
这里将未知的外部扰动看作模型的不确定性,忽略摩擦力等因素的影响。
2 分数阶积分滑模控制
图4所示为水下机械手对航行器轨迹跟踪控制的框架。系统利用传感器得到每个采样时刻目标观测点的位姿信息,并对该信息进行处理,以获得各个时刻的包含六自由度位置和姿态的齐次变换矩阵,经过逆运动学求解,得到相应的机械手末端的期望关节轨迹,在经过观察和反馈、并与实际的关节轨迹进行比较后获得系统的跟踪误差。采用分数阶积分滑模面来设计控制器的输入,其输出结果作用于控制对象以形成完整的闭环系统。
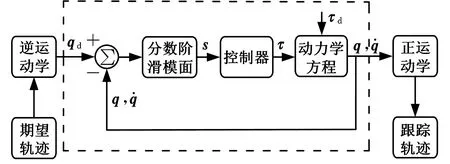
图4 轨迹跟踪控制过程Fig.4 The trajectory tracking control process
2.1 控制器设计
令qd为给定的二阶可微的期望关节矢量,定义跟踪误差e=qd-q,e=(e1,e2,…,e6)Τ。设计分数阶积分滑模面:
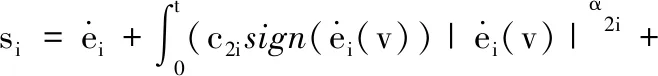
(3)
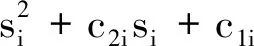
(4)
0<α2i<1i=1,2,…,6
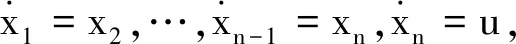
在滑动阶段,si(t)=0(i=1,2,…,6), 即
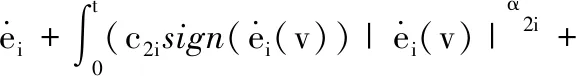
(5)
并且它的导数为
(6)
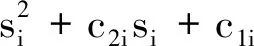
设计控制输入:
(7)
s=[s1s2…s6]Τc1=diag(c11,c12,…,c16)
c2=diag(c21,c22,…,c26)
(sign(ei)|ei|α1i)i=
[sign(e1)|ei|α11… sign(e6)|e6|α16]T


对s关于时间求导数,结合式(3)和式(7),可得
(8)
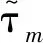
2.2 稳定性分析
考虑一个正定李雅普诺夫函数
(9)
对(9)关于时间求导数,并且利用式(8)得到:
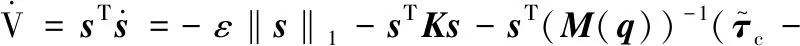
(10)
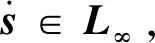
3 仿真
机械手连杆参数a2=5 m,d1=1.195 m,d3=0.7 m,d4=6.4 m,d5=-0.7 m,d6=-0.995 m,连杆密度为2 700 kg/m3。假设水下机械手的重力和浮力的中心是一致的,重力加速度为9.8 m/s2,水密度为1 025.9 kg/m3,流速为(0.5,0.5,0)m/s;水阻力系数Cd=0.6;附加质量力系数Cm=1。式(3)中的滑模面参数设为:c11=100,c12=120,c13=120,c14=100,c15=100,c16=100,c21=50,c22=60,c23=60,c24=50,c25=50,c26=50,α2i=0.9,i=1,2,…,6。目标航行器的动力学方程参数取值参考文献[16-17],如表2所示。考虑航行器在基坐标系下的z=0.5 m平面上运动。整个系统是基于计算机数值模拟进行的,以检验所提出控制律的有效性。
趋近律参数ε=0.5、ki=30,外部干扰τd为分量在[-100,100]N·m范围的随机分布向量,仿真结果见图5。图5所示为机械手末端的跟踪轨迹和航行器的运动轨迹,可以看出在t=0时二者的初始位置的距离较远,随着时间的推移,最终使得它们的位置相差很小。二者在X方向、Y方向上的位置误差如图6、图7所示,可以看出这两个位置误差约在t=2.5 s、t=1 s时首次达到误差零点,并且在后面的时间里分别实现约为[-0.02,0.02]m、[-0.01,0.01]m的稳态误差响应。由于控制器的不连续性以及外部干扰的影响,使得在X方向、Y方向上的位置误差都会产生一定程度的抖振现象,这从局部放大图中可以看出。
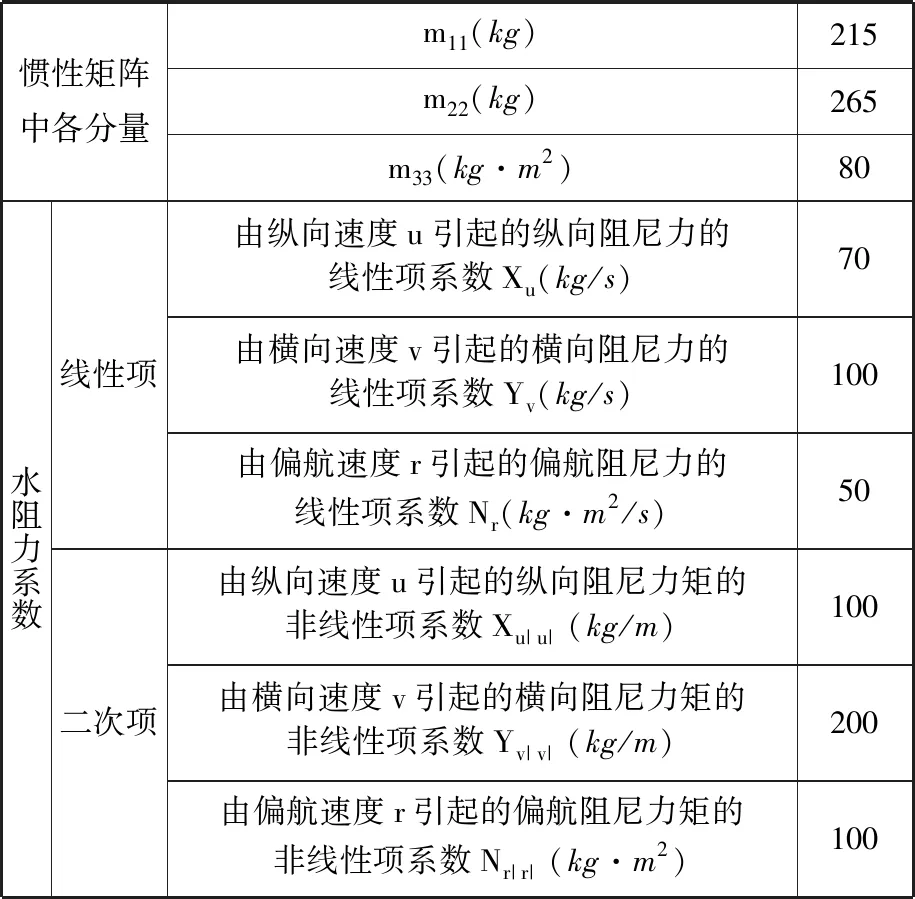
表2 目标航行器动力学方程参数Tab.2 The parameters of the dynamics equation for the target vehicle
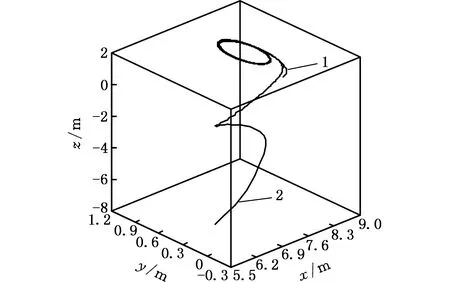
1.目标轨迹 2.机械手跟踪轨迹图5 存在干扰 [-100,100]N·m条件下的运动轨迹Fig.5 The trajectory with disturbance [-100,100] N·m
趋近律参数ε=0.5、ki=30,无外部干扰时的仿真结果如图8、图9所示。在X方向、Y方向上的位置误差仅在不连续性的影响下产生较小的抖振。
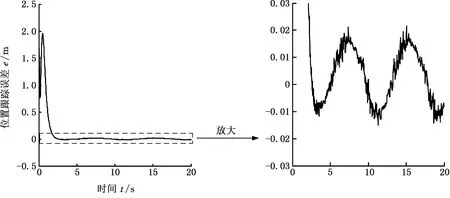
图6 存在干扰 [-100,100]N·m条件下的X方向的位置跟踪误差Fig.6 The tracking error in X direction with disturbances [-100,100]N·m
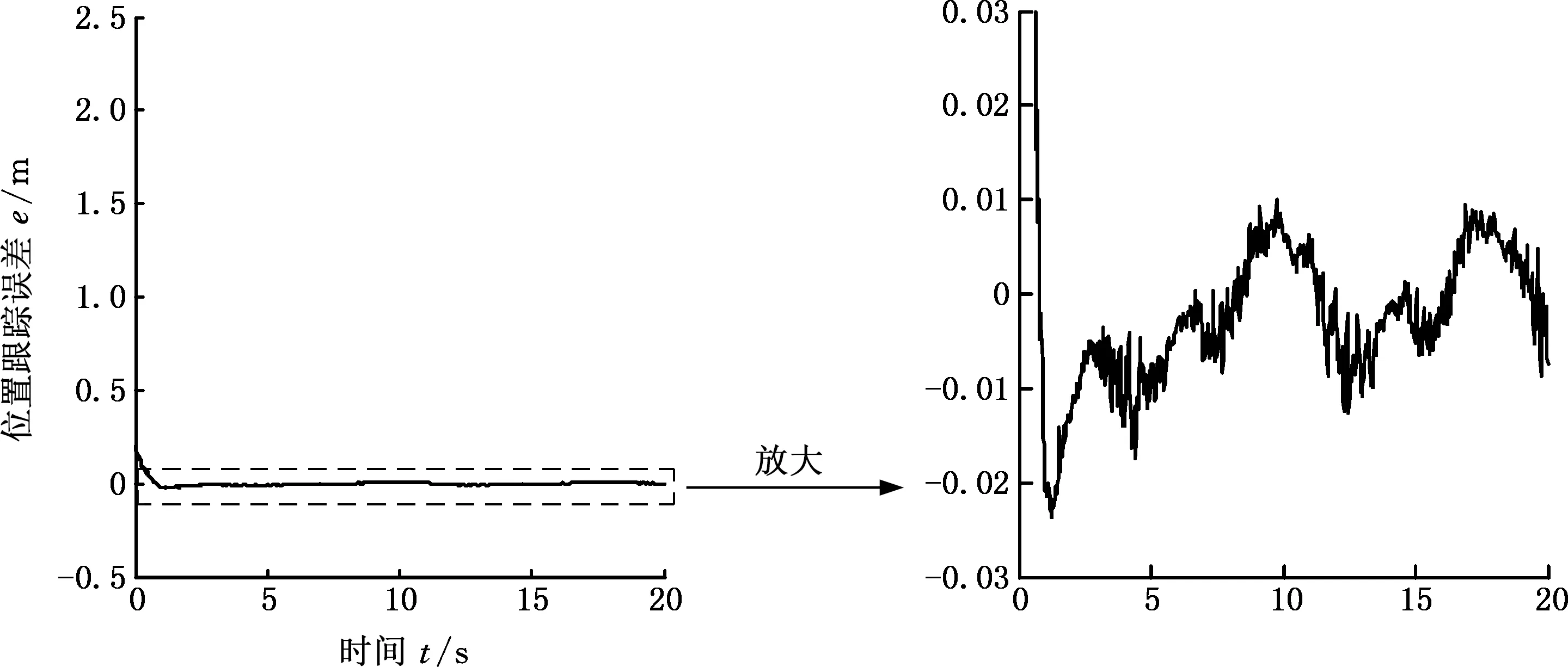
图7 存在干扰 [-100,100]N·m条件下的Y方向的位置跟踪误差Fig.7 The tracking error in Y direction with disturbance [-100,100]N·m
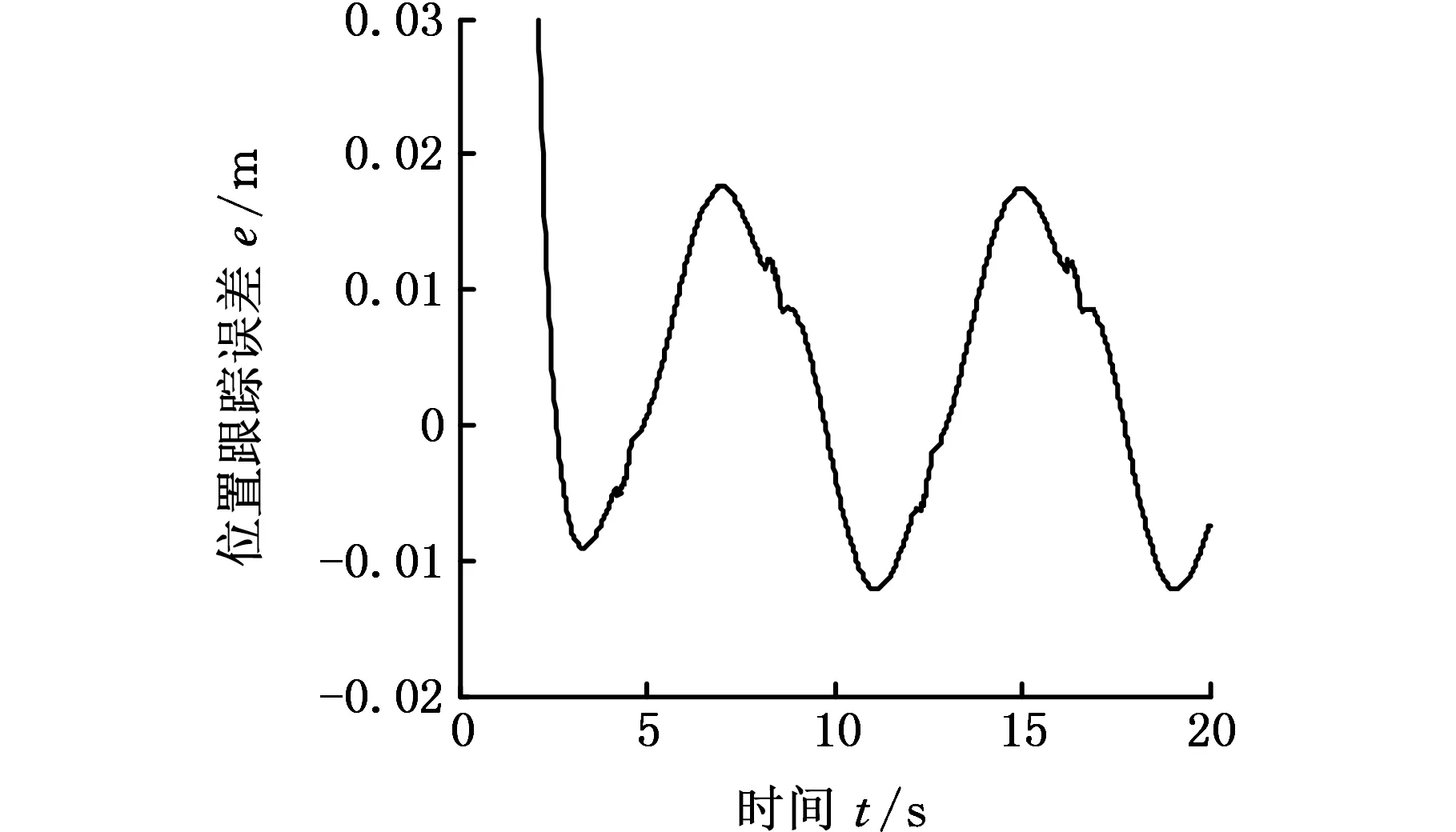
图8 无干扰条件下的X方向的位置跟踪误差Fig.8 The tracking error in X direction without disturbances
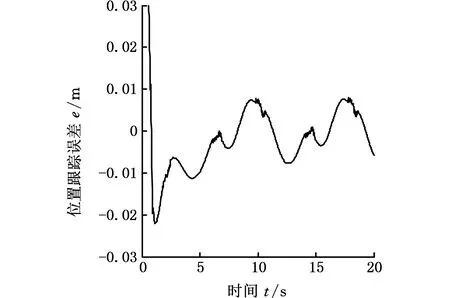
图9 无干扰条件下的Y方向的位置跟踪误差Fig.9 The tracking error in Y direction without disturbances
趋近律参数ε=0.5、ki=30,外部干扰τd为[-50,50]N·m的随机分布向量,此时的仿真结果如图10、图11所示。
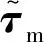
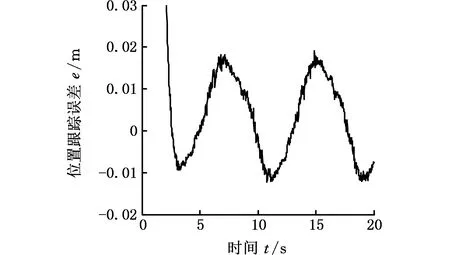
图10 存在干扰[-50,50]N·m条件下的 X方向的位置跟踪误差Fig.10 The tracking error in X direction with disturbance [-50,50]N·m
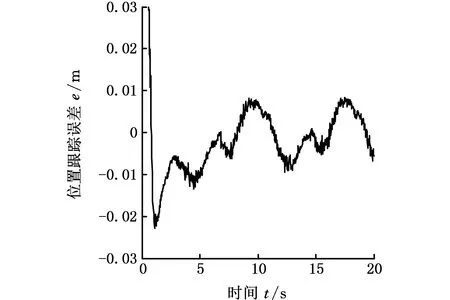
图11 存在干扰 [-50,50]N·m条件下的 Y方向的位置跟踪误差Fig.11 The tracking error in Y direction with disturbance [-50,50]N·m
4 结论
本文提出了一种分数阶积分滑模控制方法,对于未知外部扰动下的水下机械手的轨迹跟踪问题,在模型中添加了外部扰动的近似估计项,使得系统可以实现快速收敛,而且还具有较强的抗干扰能力。对六自由度水下机械手的跟踪问题进行了仿真,结果表明,该控制系统不仅能够实现高精度的轨迹跟踪性能,而且还具有较强的抗干扰能力,从而验证了该控制器的有效性。
