第三代轮毂轴承凸缘端面跳动的测量
2019-07-28陈於学沙伟张黎赵兴新赵晨昱
陈於学,沙伟,张黎,赵兴新, 赵晨昱
(1.华中科技大学 机械学院仪器系,武汉 430074;2.重庆长江轴承股份有限公司,重庆 401336)
轮毂轴承单元是汽车的关键零部件,其质量的优劣直接影响整车的运行性能。汽车用第三代轮毂轴承单元(以下简称轮毂轴承)的主要组成部分有内圈、钢球、保持架、外凸缘、凸缘、车轮螺栓等。轮毂轴承凸缘通过螺栓与制动盘轮辋连接。凸缘端面的跳动会产生不平衡惯量,使车轮产生离心力,此离心力的方向随车轮的转动而变化,对车辆的动、静态特性产生严重的影响[1-2]。目前,采用检测人员手动旋转轴承,通过人眼观察扭簧表读数确定检测数值的方法进行端面跳动的测量,这种方法比较繁琐且人为因素对测量结果的影响比较大[3]。同时,不同型号轮毂轴承凸缘端面具有不同数量的缺口,这些缺口的存在大大增加了人工测量的难度。
综上,提出一种新型的以LabVIEW为平台的轮毂轴承凸缘端面跳动测量方法,可以有效消除由于安装和装置本身端面倾斜导致的系统误差,从而得到准确的端面跳动测量结果[4]。
1 测量原理
如图1所示,不同型号轮毂轴承的凸缘端面可以分为连续端面和离散端面2大类,或者无缺口型、单缺口型、四缺口型3小种。

图1 不同端面的轮毂轴承凸缘
1.1 测量方法
根据轮毂轴承凸缘端面上的螺栓实际安装情况,并结合大量的试验,采用如图2所示的测量原理。利用一面两孔定位原理定位被测物,将被测轴承置于放置平台,然后将被测轴承上的车轮螺栓插入放置平台的孔中,再利用锁紧螺母将被测轴承锁紧。传感器垂直接触轮毂轴承凸缘端面,通过静压主轴带动被测轴承一起匀速旋转,测量轮毂轴承凸缘端面上的整个圆周。3种不同形状端面的测量结果如图3所示。
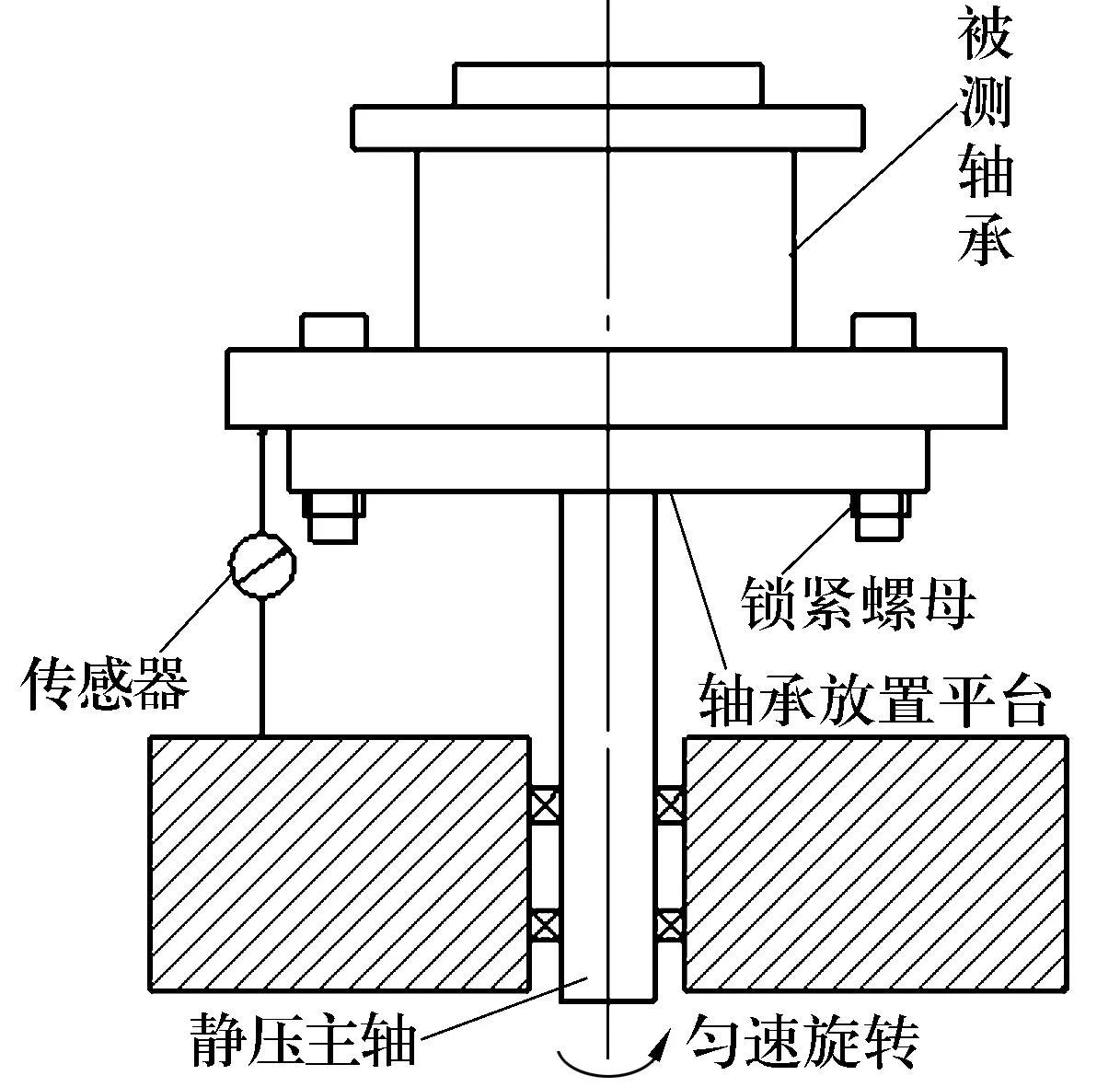
图2 轮毂轴承凸缘端面跳动测量原理示意图
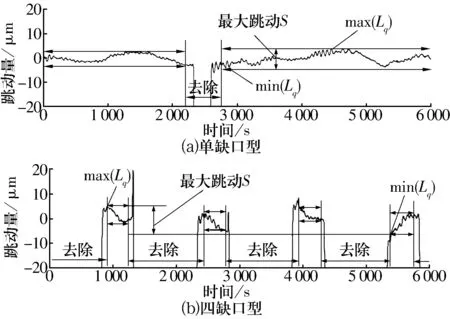
实际测量得到的3种波形呈现正弦波形趋势,如果采集更多圈数,正弦波形就会周期性的波动下去,符合旋转零件的测量情况[5]。但是,这种宏观上的正弦变化并不是轮毂轴承凸缘端面跳动量的实际情况,这是由于轮毂轴承安装平台的倾斜或者安装轴承时轴承轴线倾斜所导致的结果。
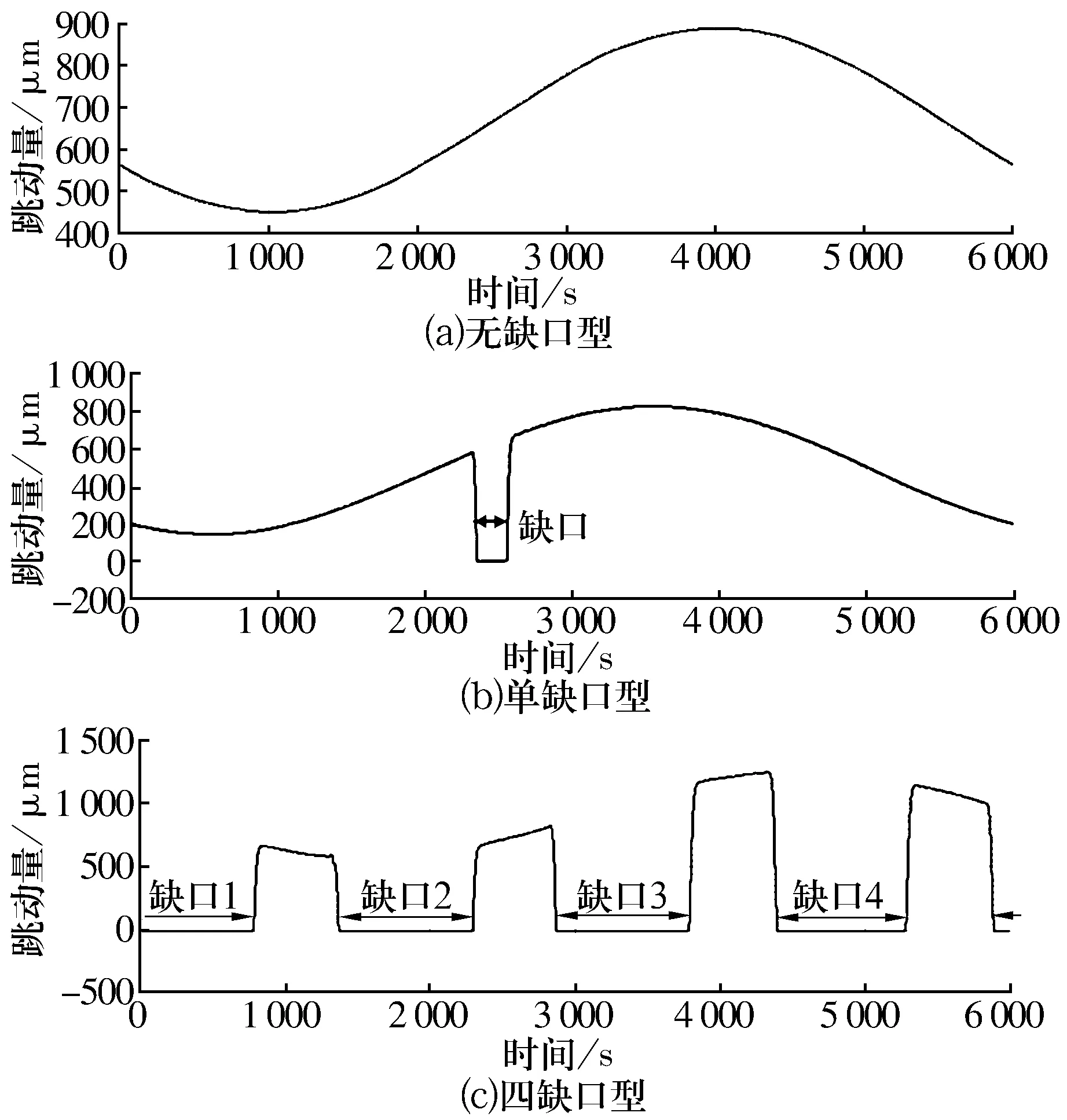
图3 轮毂轴承凸缘端面跳动采集数据
1.2 误差消除和凸缘端面跳动获取
1.2.1 端面测量中的误差分析
如图4所示,测量中端面保持理想水平,直接测量得到的就是实际的端面跳动量S。理想情况下得到的测量数据应当是一条直线,位移传感器的示值始终为初始值P0,如图5所示。但在实际测量过程中,被测轴承的凸缘端面可能是倾斜的,导致位移传感器触头与被测轴承凸缘端面接触点的空间运动轨迹是一个椭圆,这种情况下的测量数据不是端面的真实跳动量。

图4 被测轴承测量示意图
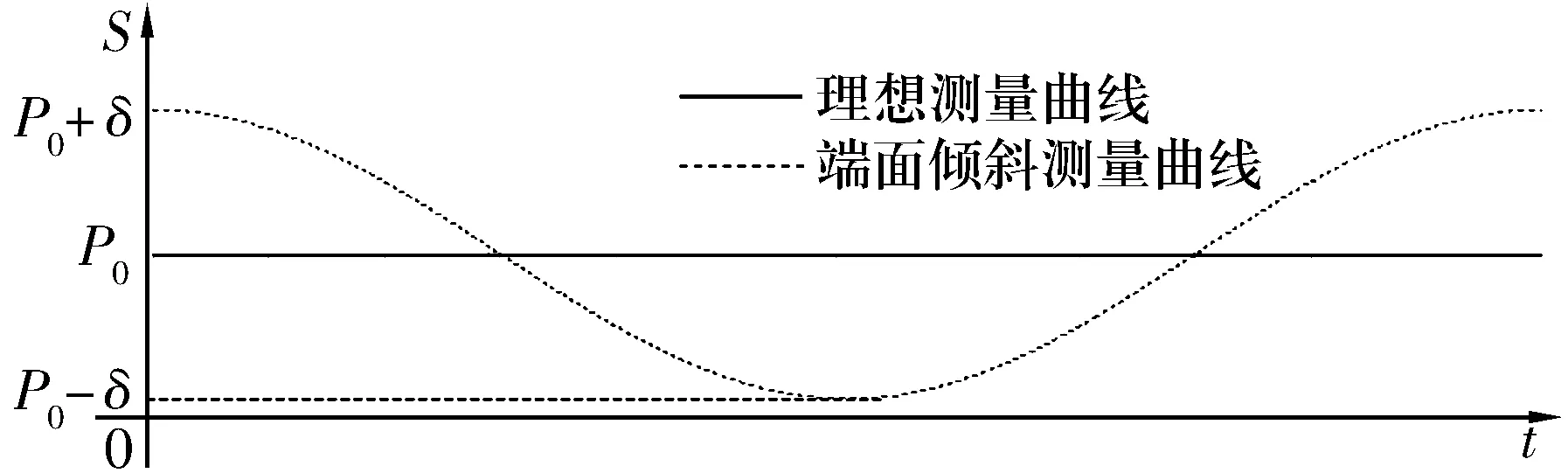
图5 理想水平测量数据
测量过程简化的模型如图6所示,此运动轨迹可以看作由一个圆柱和一个空间平面斜相交所导致。设圆柱和空间平面的方程分别为
x2+y2=R2,
(1)
Ax+By+Cz=D,
(2)
式中:R为位移传感器触头到轴线的垂直距离;A,B,C,D为常数且不等于0。
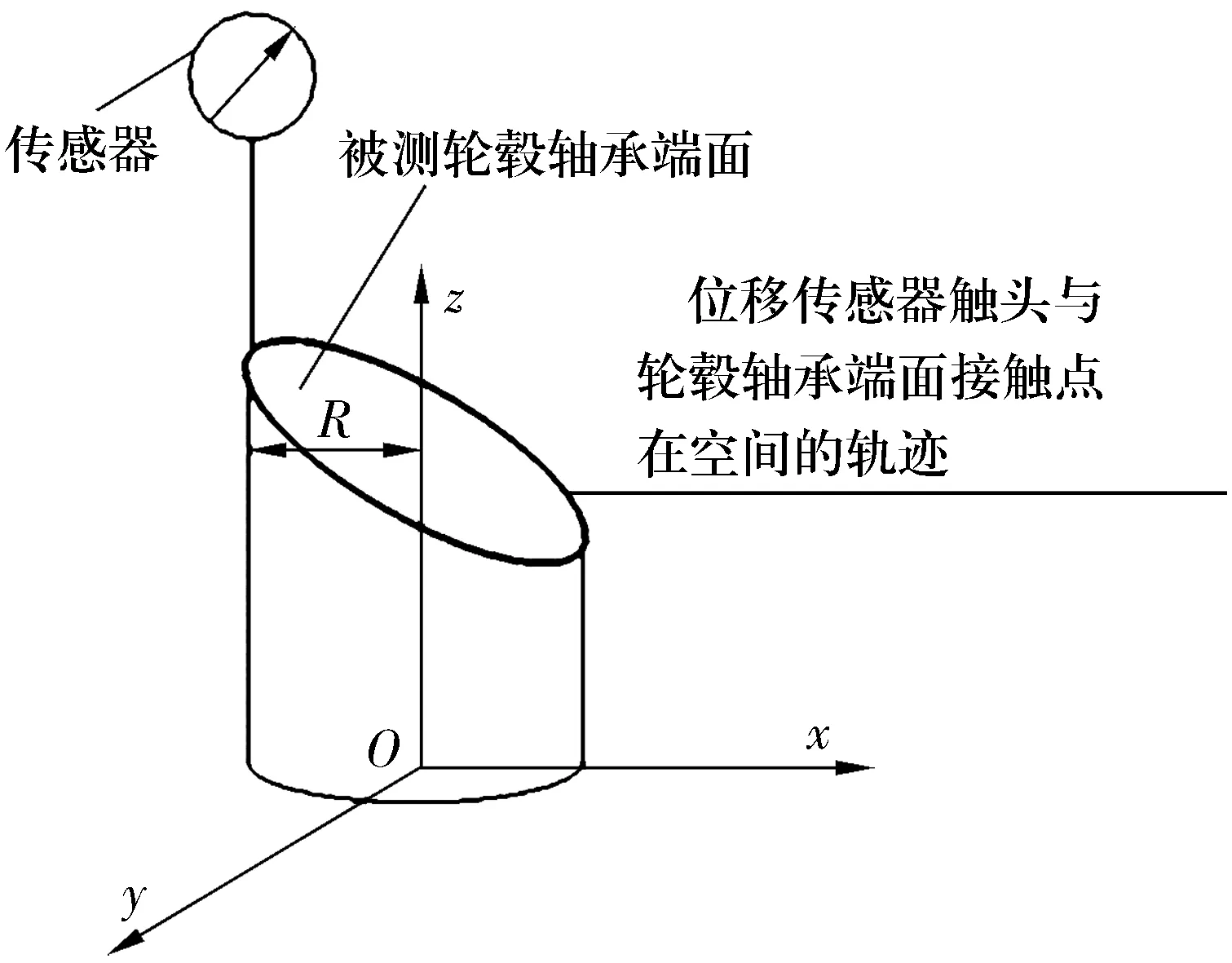
图6 轮毂轴承凸缘端面被测点在空间的运动轨迹
再令x=Rcost,y=Rsint,t∈(0,2π),代入(2)式化简可得
z=P0-δsin(t+θ),
(3)

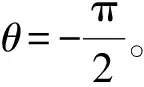
由于位移传感器的示值只与z轴方向变化有关,(3)式中z的变化就是位移传感器示值的变化,其表达式也证明了如果轴承凸缘端面出现图4中的倾斜,测量得到的数据应该如图5中虚线所示。而图3所示实际测量数据呈现明显的正弦趋势,证明实际测量过程中确实存在这种系统误差,所以在测量中消除这种系统误差才能得到准确的跳动量。
1.2.2 极坐标变换法消除误差
按照以下步骤可从原理上消除端面倾斜引起的系统误差。
1)根据伺服电动机带动静压主轴的转速和位移传感器的采样频率,得到旋转1周的总采样点数N为
(4)
式中:n为主轴旋转的速度,r/min;f为采样频率,Hz。
2)在实际测量中采集的信号数据点多于N,消除误差时只需要一整个圆周的信号即可,所以截取整个圆周N个数据点进行极坐标变换,对于任意一点(tk,sk),k=1,2,…,N,tk为采集信号的点数,sk为传感器的示数,将其从t-s坐标系变换到极坐标系
(5)
式中:θk,ρk为极坐标下的坐标值。
由于极坐标不好计算且难以建立数学图像,而直角坐标系下求取跳动更加方便和直观,因此再将其转化到直角坐标系下,进行以下变换
(6)
式中:xk,yk为直角坐标系下横、纵坐标值。
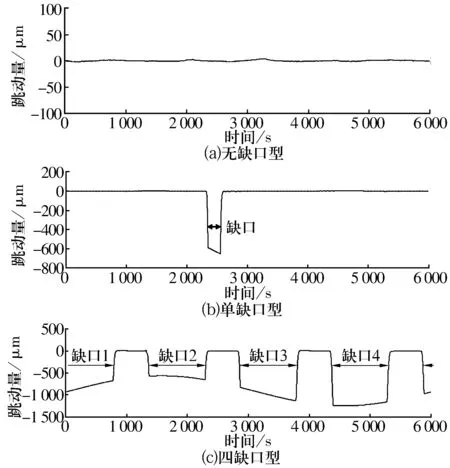
3)提取变换之后的数据点(xk,yk)进行最小二乘拟合圆,即
(7)
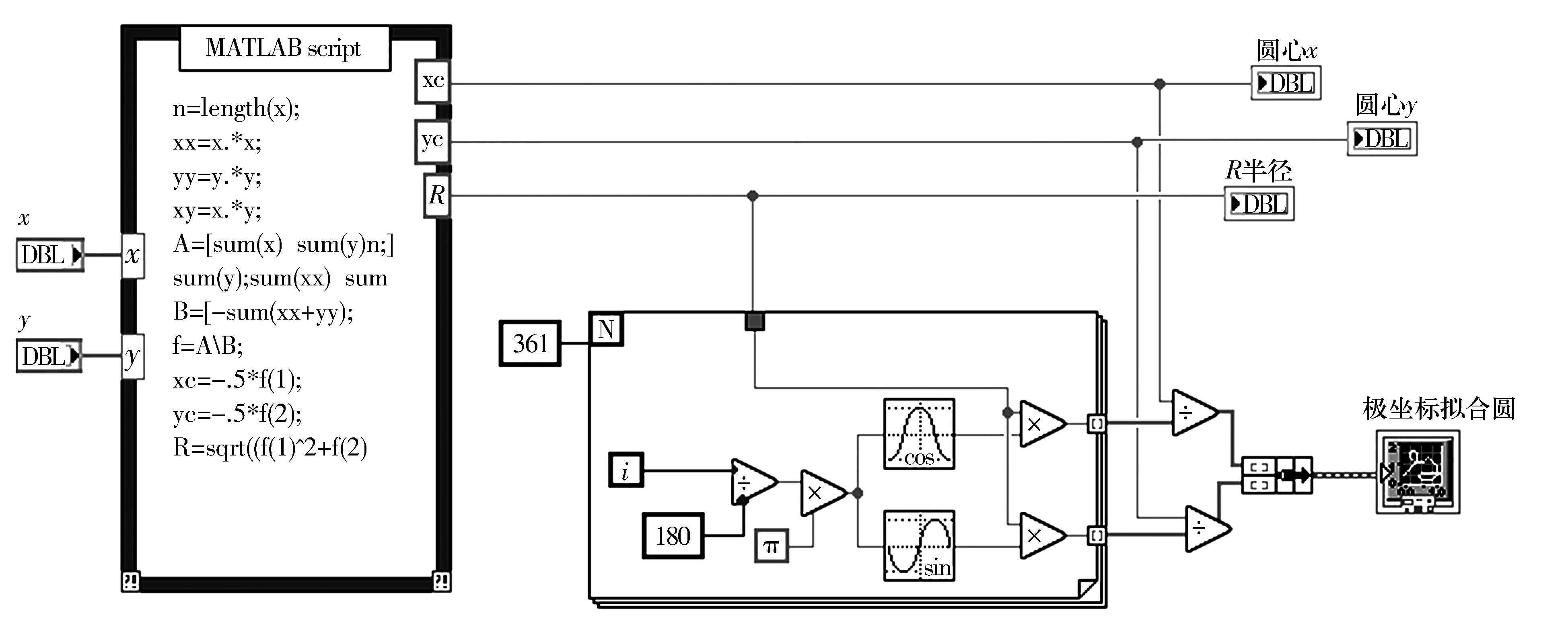
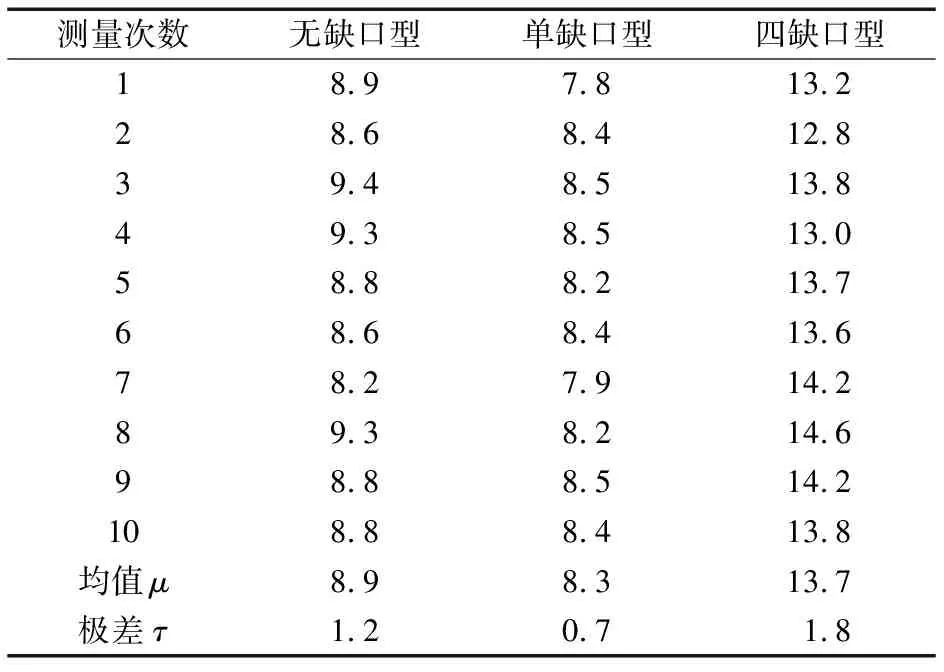
式中:f(x)为待拟合的方程;M为选取数据点的总数,对于连续端面M=N,对于离散端面M f(x)的函数模型为(x+x0)2+(y+y0)2=r2,所以可以利用最小二乘拟合方法得到圆心O1的坐标(x0,y0)和半径r,如图7所示。拟合出来的半径r实际上就是倾斜量δ。 图7 拟合圆示意图 4)对拟合后的任意点P(xj,yj)进行(5)式和(6)式的反变换得到P0(tj,sj),j=1,2,…,N。 则消除误差后的数据为 Lk=sj-sk。 (8) 图3中的数据经消除误差后如图8所示,对比可知:图3中的原始信号有明显的正弦趋势,这种趋势就是由于端面倾斜导致的系统误差,在经过上述的方法消除误差之后,这种趋势被明显消除。 图8 轮毂轴承凸缘端面消除误差后的跳动数据 1.2.3 端面跳动信号提取 由于轮毂轴承凸缘端面的形状并不单一,所采集到的端面信号不能全部使用,需要对采集信号进行提取。将采集到的轮毂轴承凸缘端面信号分为连续端面跳动信号和离散端面跳动信号进行分析。 1)连续端面跳动信号提取 对于无缺口型轮毂轴承凸缘,采集到的是连续端面跳动信号,位移传感器在整个测量过程中都与被测表面接触,所以采集到N个数据点的信号都是准确可用的,消除误差后的数据点sk如图9所示,则连续轮毂轴承的端面最大跳动为 SC=max(Lk)-min(Lk)。 (9) 2)离散端面跳动信号提取 相对于无缺口型轮毂轴承凸缘采集到的连续端面信号,离散端面跳动信号复杂一些。由于凸缘端面有缺口,采集过程中位移传感器在有缺口的地方没有与端面接触,会造成相应信号的缺失,如图3b和图3c所示。同时,当凸缘从缺口处旋转到与位移传感器接触时,此过程产生的撞击会极大地影响传感器的采集精度。 SD=max(Lq)-min(Lq)。 (10) 图10 离散端面跳动信号提取 基于上述测量原理进行轮毂轴承凸缘端面跳动测量试验。试验由2大部分组成:1)机械部分,利用伺服电动机,通过同步带传动带动静压主轴旋转实现被测轴承凸缘的旋转,并固定传感器;2)控制和信号采集系统,主要包括控制伺服电动机的转动和轮毂轴承凸缘端面跳动信号的采集、转换和处理,并得到最终的跳动量。 测量装置如图11所示,具体测量步骤如下: 1)将被测轴承置于放置台,尽可能使被测轴承凸缘端面与放置平台之间的安装倾斜度为零,调节锁紧螺母将被测轴承锁紧。 2)将电感位移传感器安装好,旋转调节螺母,使传感器在整个回转过程中保持在一半量程左右,同时不能与被测轴承发生干涉。 3)启动油泵和工控机,使伺服电动机运转,通过同步带带动静压主轴和被测轴承做同步匀速回转运动。 4)等待被测轴承的回转运动稳定,运行LabVIEW采集程序,将传感器所采集1个周期的端面跳动信号经过A/D转换器传输到计算机,在LabVIEW中经过数据处理显示出测量结果。 1—同步带;2—静压主轴;3—回转轴;4—轴承放置平台;5—被测轮毂轴承;6—总体机架;7—工控机;8—位移传感器;9—传感器锁紧件;10—传感器固定架;11—传感器调节架;12—伺服电动机;13—电动机固定架 轮毂轴承凸缘端面跳动信号的采集采用虚拟仪器技术,利用LabVIEW编程实现数据采集、信号显示、数据处理及存储读取等功能[6]。主要的子程序如图12—图14所示。 取3种型号的轮毂轴承各1套,进行10次装夹,每次装夹好测量1次凸缘端面跳动,测量结果见表1。由表可知,3套轴承各自的10次测量结果极差为±2 μm,相比采用手动千分表进行端面测量时6~7 μm的精度有很大提高,测量系统的重复性精度达到了预期要求。 图12 端面跳动信号最小二乘拟合子程序图 图14 离散端面信号截取子程序图 表1 轮毂轴承端面跳动试验测量结果 介绍了一种基于LabVIEW的轮毂轴承凸缘端面跳动测量方法,利用极坐标和直角坐标变换消除了端面倾斜系统误差。多次重复试验数据证明此方法可以达到预期要求的测量精度。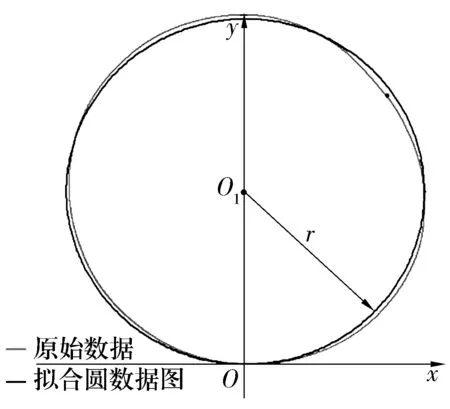
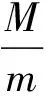
2 试验设计
2.1 机械测量装置

2.2 系统软件设计
3 试验结果

4 结束语
