基于结构张量空间模型的文本分类
2019-07-26庄建昌洪彩凤顾兴全
庄建昌,武 娇,洪彩凤,顾兴全
(中国计量大学 a.理学院;b.标准化学院,浙江 杭州 310018)
一、引言
自然语言处理(Natural Language Processing,NLP)在人工智能中占据着重要的地位。自然语言处理的任务是使用计算机并结合机器学习算法处理各类文本数据、挖掘文本信息。文本数据是一种非结构化的数据,计算机无法直接对文本进行处理,因此必须将其转变成结构化的数据,才能开展进一步的文本作业。文本数据的结构化表示对后续工作有直接的影响,因此文本的表示模型是文本处理领域的一个研究热点。
到目前为止,传统的向量空间模型(Vector Space Model,VSM)是文本表示的主流模型[1]。该模型将文本转化为向量的形式,向量中各维度的值对应着文本的各个特征。由于VSM操作简单,容易理解,在自然语言处理领域倍受关注,许多相关工作都是以VSM为基础开展的[2-4]。但是基于VSM的文本表示假设文本特征是相互独立的,导致文本的语义信息丢失,因此,一些学者针对此问题进行了深入研究。刘怀亮等依据知网的知识系统,提出基于知网语义相似度的中文文本分类方法[3],在进行文本相似性计算时,考虑了同义词的影响。但该方法仍是以VSM为基础,并未对文本的表示模型做出修改。Liu等则依据WordNet structure来构造概念向量,并用之研究文本语义相关性[4]。所谓概念向量,就是把原本用特征来构造的向量改成用概念来表示的向量,相比较特征,概念的适应性更强,构造的向量模型维度更低。
为了解决VSM的高维度问题,Cai等通过某种规则将文本的向量表示映射成二阶张量表示,提出文本的张量空间模型(Tensor Space Model,TSM),并基于此模型提出支持张量机(Support Tensor Machine,STM)算法解决文本分类问题,实验证明了TSM在小样本数据下较传统模型更具有优势[5]。俞炯等通过对小样本及数据不平衡情况下的文本分类实验,也证实了TSM优于传统VSM模型[6]。何伟等将TSM与KNN(k-nearest neighbors algorithm)结合进行文本的多分类实验,结果表明多分类任务中,TSM也优于VSM[7]。
由于利用张量表示数据能够有效地降低数据特征维度和较好地保持数据结构,因此近年来涌现出大量基于张量的算法,以及张量在图像处理、模式识别、统计模型等领域的应用研究[8-14]。在图像处理问题中,多通道图像或视频能够很自然地由三阶或高阶的张量表示,并且有效保持各分量图像或各视频帧之间的结构关系。但在文本处理问题中,张量表示能否有效地保持文本的结构信息呢?虽然有文献利用张量形式表示文本,但由文本的向量表示向张量表示的映射具有随意性,形成的张量空间模型不能明确体现文本的结构特征[5-7]。因此,有必要对文本的结构信息进行挖掘,以构造更具结构特征的张量空间模型。
Salton认为文本的最小结构单位是段落,提炼文本的结构信息有利于文本检索,以及提取长文本不同的主题概念[15]。林鸿飞等提出基于概念的文本结构分析方法,其中文本结构被定义为文本的层次[16]。他们认为文本的层次与层次之间应具有如下特性:同一层次下的段落尽可能相似,不同层次下的段落尽可能相异。基于这种特性可以提取文本的层次结构。受到以上工作的启发,在本文中,我们首先提出一种文本层次结构提取算法(Hierarchical Structure Extraction Algorithm,HSEA),提取文本层次结构信息;其次将提取的层次结构信息应用于文本的表示,提出一种新颖的基于文本分层表示的结构张量空间模型(Structured Tensor Space Model,STSM);最后,我们将文本的结构张量表示与一种基于交替优化的高阶支持张量机算法结合应用于文本分类。在文本分类实验中,与基于VSM的支持向量机分类算法和基于TSM的支持张量机分类算法进行了比较,实验结果表明,在小样本数据下,本文的方法能够获得更优的分类效果。
二、结构张量空间模型
(一)向量空间模型到张量空间模型
对语料库中任意的一个非结构化的文本f,传统向量空间模型将其表示为一个结构化的向量w=(w1,w2,…,wN)∈RN,如图1所示。向量w的维度N是生成VSM表示的词典(Vocabulary)中所包含词(Term)的个数,w的每个分量表示文本的一个特征,其中第n个分量wn对应着第n个词的某种统计量。根据不同的工作任务,这些特征可以取为词频、词频—逆文档频率、信息增益、互信息和期望交叉熵等,不同的特征反映文本不同方面的信息。由于文本语料中包含的词汇量巨大,因此文本的VSM表示通常具有高维度、高稀疏度的特点,此外如前文所述,VSM不能体现文本的语义信息。

图1 向量空间模型图
为此,Cai等人提出文本的张量空间模型(TSM),通过使用某种规则建立从VSM到TSM的映射关系,将文本f的VSM表示向量w∈RN转变为一个2阶张量,即矩阵W∈RN1×N2,如图2所示[5]。图2(a)将一个9维的向量w转化为的3×3的矩阵W,图2(b)通过补0将w转化为5×2的矩阵W。一般地,当N1×N2>N时,可先对原N维向量补0,再将其转化为N1×N2的矩阵。在文本处理时,通过从VSM表示到TSM表示的转换,模型参数的数量将从N下降为N1+N2,可有效地避免维度灾难。
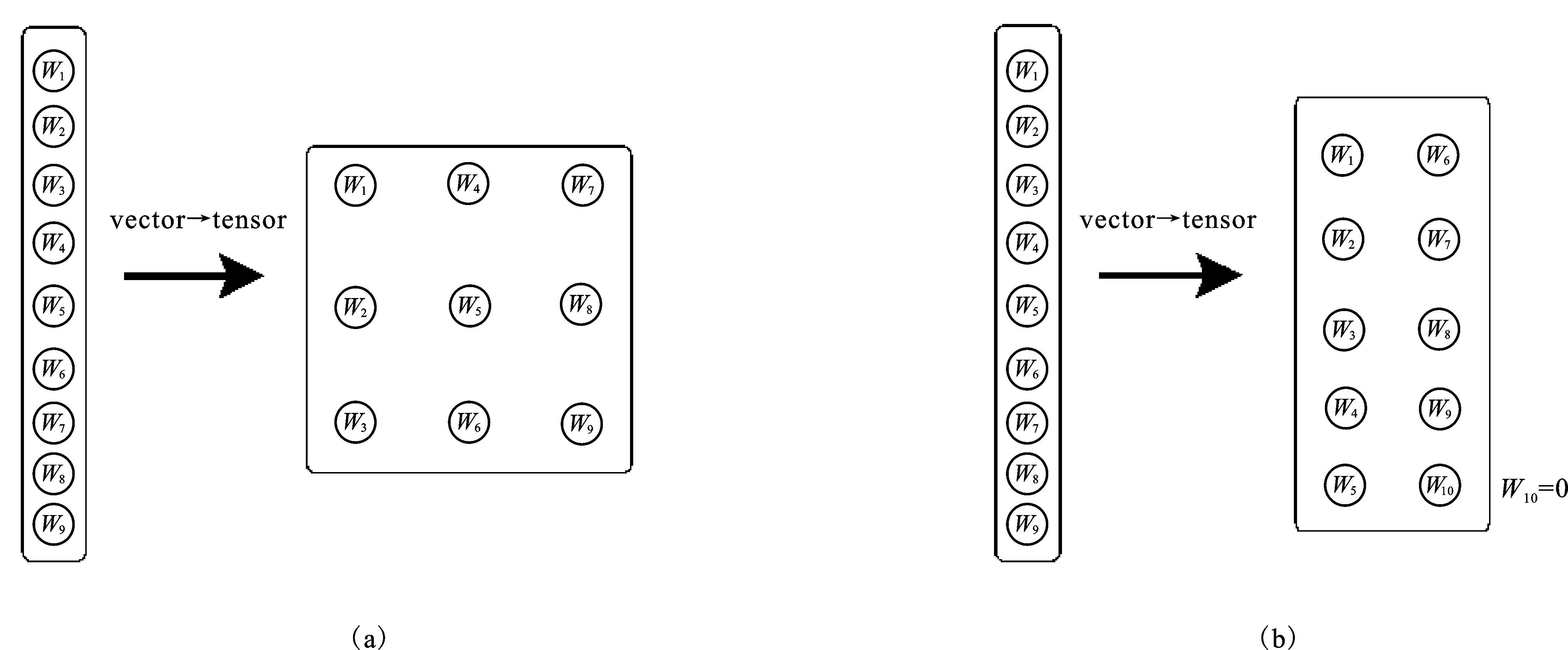
图2 VSM到TSM的映射图
从图2可以看到,一个向量可以被映射为不同维度的矩阵,映射方式具有随意性,Cai等没有给出一种确定的映射规则,并且由此形成的2阶TSM不能明确地体现文本的结构特征。为此,在下文中我们将文本的层次信息融入文本表示,得到更具结构性的文本表示模型。
(二)结构张量空间模型
1.文本的分层表示

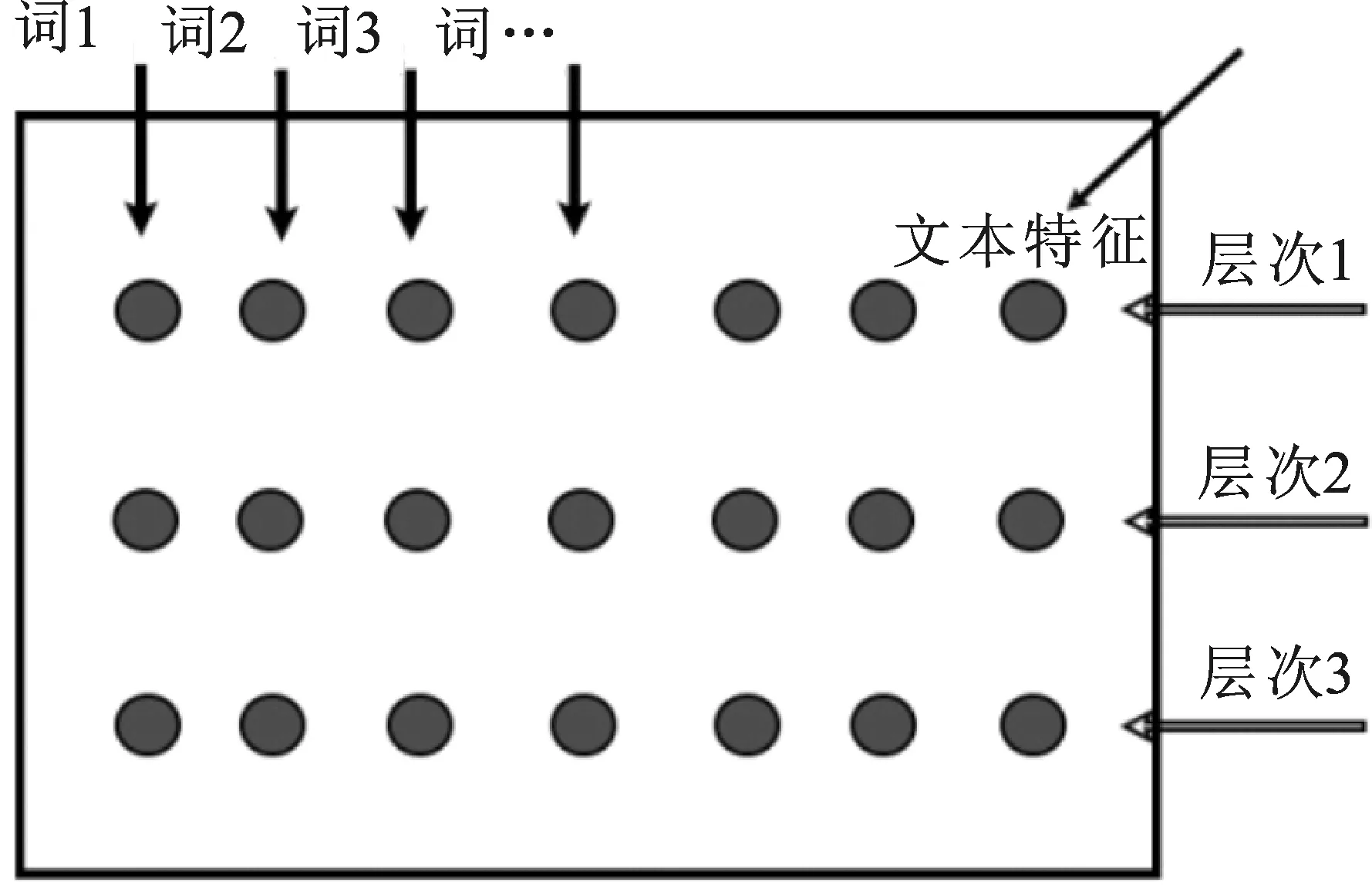
图3 文本的分层表示模型图
我们按以下原则提取文本层次结构[16]:
(1)段落为文本最小的结构单位,文本的层次由段落按先后顺序聚合而成;
(2)同一层次中的段落含义尽可能相似,不同层次中的段落含义尽可能相异。

定义:分层评价函数(Hierarchical Evaluation Function,HEF)
(1)
其中,Sinter是层间离散度,度量不同层次之间的距离;Sintra是层内离散度,度量同一层次内段落之间的距离。按上述层次结构提取原则,合理的层次结构应当使Sinter尽可能大,Sintra尽可能小,也就是使JHEF最大。Sinter与Sintra计算公式如下:
Sinter=∑i∑jd(pij,mi)
(2)
Sintra=∑iPi·d(mi,m)
(3)

(4)
(5)
d(·)为距离函数,度量两个向量之间的距离,本文使用余弦距离。
基于上述思想,本文提出文本层次结构提取算法(HSEA)。给定将要提取的层次个数L,HSEA首先将所有的段落并入一个层次,通过迭代的过程逐步进行层次的切分。假设在第i次迭代时,获得文本第i个层次的最优切分,那么第i+1个层次的最优切分是通过在第i个层次中遍历所有可能的分割点,选取最大化HEF值的分割点进行切分得到的。此过程重复进行,直到获得L个层次为止。
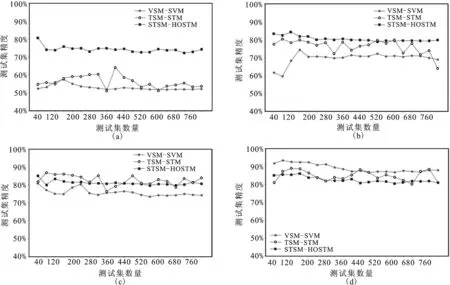
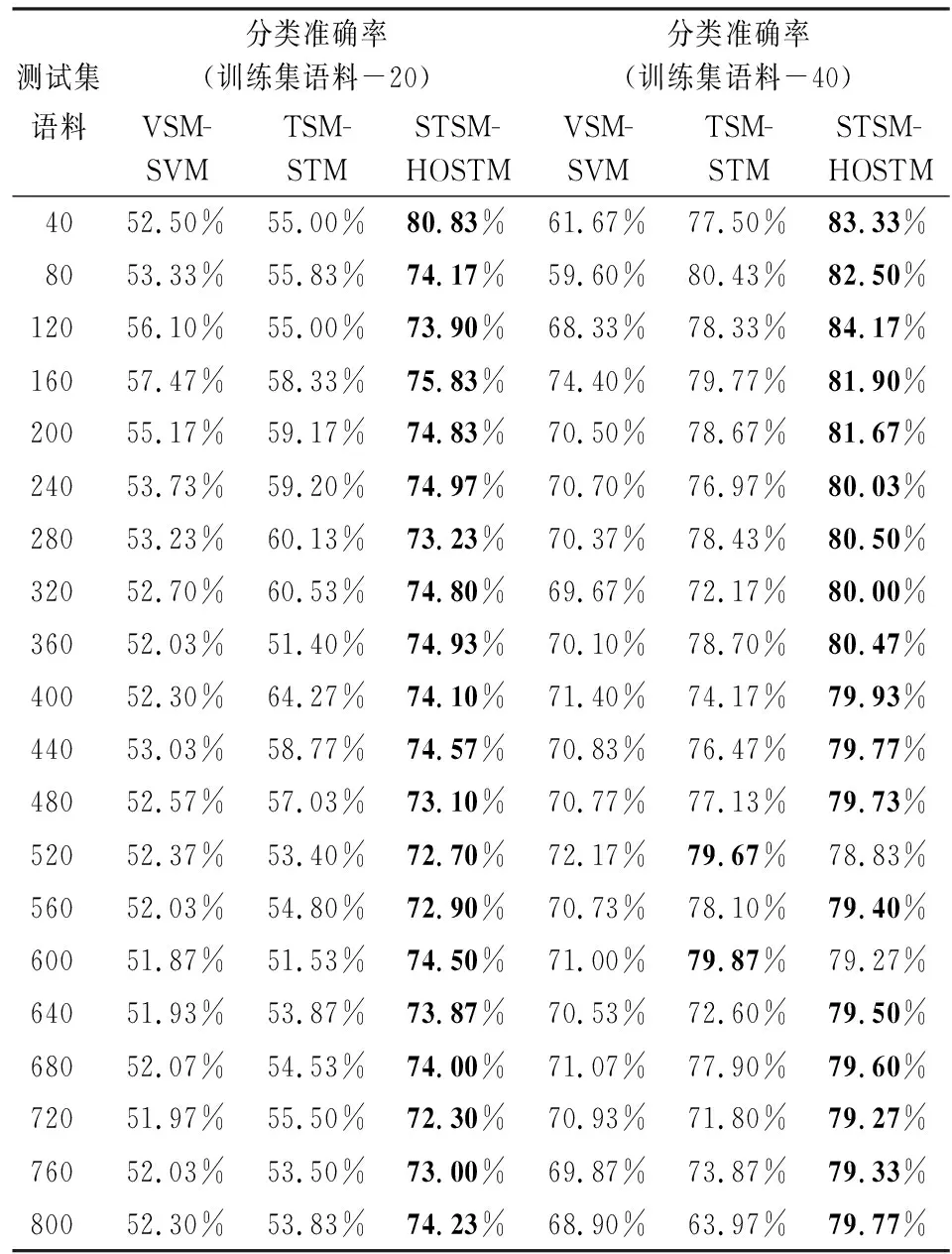
HSEA在每次提取新的层次时,需要遍历所有可能的|K|个分割点,计算相应分层结构的HEF值,这里|K|为分割点候选集K中分割点的个数。对段落总数为P的文本,获得层次个数为L的分层结构,由于|K| 在获得文本f的层次结构集Ph={Ph1,Ph2,…,PhL}后,使用语料库词典,将每个层次用VSM表示为向量形式,记第i个层次Phi的VSM表示向量为wi∈RN,那么文本f的分层表示即为如下矩阵形式: (6) 2.基于分层表示的结构张量空间模型 从式(6)可以看出,文本分层表示模型实际上是一个嵌入了文本层次结构的2阶TSM。但是在该模型中,文本的结构(即,层次)由高维的VSM表示,因此形成的2阶TSM具有高维度的缺点。为此,本文结合TSM中使用的由VSM到TSM的映射方法,将分层表示模型进一步转化为3阶的TSM,如图4所示。我们定义这个新的文本表示模型为基于分层表示的结构张量空间模型(Hierarchical Representation-based Structured Tensor Space Model,HR-STSM)。 图4 基于分层表示的结构张量空间模型图 在上一节中已得到文本f的分层表示矩阵W∈RL×N,下面我们将每个层次的VSM表示向量wi∈RN映射为矩阵Wi∈RM×M(i=1,2,…,L),其中矩阵的维度M由式(7)计算, (7) 从而得到文本f的HR-STSM表示,记为X∈RM×M×L。 将文本的高阶结构张量空间模型应用于文本分类的一个重要问题是设计能够处理张量结构数据的性能良好的分类算法。近年来,作为支持向量机(Support Vector Machine,SVM)方法的延伸,支持张量机(Support Tensor Machine,STM)在图像处理、文本处理等许多领域都备受关注,并由不同的出发点扩展出不同的张量算法。 与SVM相似,STM学习的最终结果也是找到能够最大程度分隔两类样本的最优分类超平面。STM的分类平面为 (8) 其中αk为k-mode模式参数向量,X×kαk表示张量X与αk的k-mode积,b为分类阈值,K是张量的阶数(本文中K=3)。 STM分类问题的目标函数为 (9) 其中,ξ=(ξ1,ξ2,…,ξD)T表示松驰变量,α1∘α2表示向量α1和α2的张量积。 求解优化问题(9)时,参数αk的确定依赖于其它的参数αl(1≤l≤K,l≠k),一般使用交替优化方法对参数进行求解。也就是说,在求解某个参数αk时,将其余的参数αl(l≠k)的值固定,然后交替地求解出每个参数。通过这种方法,高阶STM优化问题(9)可以被分解为一系列标准的SVM子问题进行交替求解。高阶STM算法代码可从作者的Github下载[注]Github:https://github.com/spzhuang/support-tensor-machine/create/master.。 在本章中,我们通过文本的分类实验来验证结构张量空间模型在文本分类任务上的有效性。实验包括两部分:第一部分研究了文本分层结构中层次的个数对分类性能的影响,以确定HR-STSM的最优分层数;第二部分研究了基于HR-STSM表示的高阶STM算法(简记为STSM-HOSTM)的分类效果,并与基于VSM表示的SVM算法(VSM-SVM)、基于TSM表示的STM算法(TSM-STM)的性能做出比较。 实验涉及的所有算法均采用Python 3.6.5进行实现,并在Spyder 3下进行编译与运行。程序中主要使用的软件包以及相应的版本如下:机器学习包scikit-learn(0.19.1),数值运算包numpy(1.14.3),数据处理包pandas(0.23.0),结巴分词包(0.39),张量代数运算包tensorly(0.4.2)。我们采用 libsvm 求解方法作为 SVM 算法的实现,STM和HOSTM中子优化问题的求解也使用了此方法。实验使用电脑 CPU 型号为Intel(R) Core(TM) i7-7500U,内存8GB,操作系统为Windows 10企业版。 1.搜狗新闻语料 搜狗新闻语料库[注]搜狐新闻数据:https://www.sogou.com/labs/ resource/cs.php.,是一个包含大量不同主题的网络新闻语料库。本文选取主题为IT、教育、汽车和财经4个类别的语料进行实验。语料的分布情况见表1。 表1 搜狗语料类别以及数量表 2.复旦中文语料表 复旦中文语料[注]复旦语料:http://www.nlpir.org/wordpress/download/tc-corpus-answer.rar,是一个多类中文语料库,语料中的题材多为历年来的相关文章。我们选择了类别为艺术,农业,政治三类语料进行文本实验,其数量分别见表2。 表2 复旦语料类别以及数量表 对语料的预处理包括:使用jieba分词工具对文本进行分词,去停用词处理。VSM和TSM均使用TF-IDF作为文本特征来构建文本表示模型,而在STSM模型中,对采用词频作为文本特征进行文本的分层,构建了文本的分层表示之后,进一步采用IDF加权,这意味着,在分类实验中,STSM使用TF-IDF作为特征的表示。 1.HR-STSM层次实验 本节研究HR-STSM中层次个数对分类性能的影响。实验使用IT、教育和汽车3个类别的语料,将3个类进行两两组合,共得到3个二分类组,3个类别的语料数量如表1所示。 训练集从3个二分类组中随机抽取,所包含的语料数量从100到800,每次增加100个;训练集和测试集均占语料数量的50%。在HR-STSM的层次个数分别为2、3、4、5的情况下使用HOSTM进行分类学习,利用测试准确率进行评价,测试准确率取3个二分类组的平均值。 实验结果如表3所示。可以看到4层HR-STSM的测试集分类精确度最高,因此在下面的实验中使用4层HR-STSM表示文本。 表3 层次实验结果表 注:粗体表示该组实验中的最大值。下同。 2.文本分类实验 本节对VSM-SVM 、TSM-STM和 TSM-HOSTM的分类性能进行比较,实验中三种算法的惩罚参数的弹性大小为1、50、50,以保证分类器对训练集的准确率能够不小于90%。 1)实验A:搜狗语料分类实验 实验A使用IT、教育、汽车和财经4个类别的语料,以IT语料作为正类样本,分别与其它类别语料构成3个二分类组。 实验A从两方面进行:固定语料总数,改变训练集和测试集语料比例的分类性能比较;固定训练集语料,改变测试集语料个数的分类性能比较。 第一,固定语料总数。3个二分类组包含的语料数量分别取200、400、600、800,在语料总数固定,训练集和测试集按不同比例分配(见表3第1列)的情况下,对VSM-SVM、TSM-STM和 STSM-HOSTM的分类性能比较结果见图5和表3,其中测试准确率为3个二分类组的平均值。 图5 实验A结果比较图 图5表示语料总数固定,训练集和测试集按不同比例分配变化时,VSM-SVM、TSM-STM和 STSM-HOSTM对测试集的分类准确率曲线。其中实心圆点、空心圆点和实心方块曲线分别是VSM-SVM、TSM-STM和STSM-HOSTM的分类结果。图6(a)~(d)分别为语料总数取200、400、600和800的分类结果。可以看到,在4种规模的语料总数下,当训练样本的比例较低,即训练样本包含的语料个数不超过60时,VSM-SVM的分类性能均较差,测试准确率低于70%。当训练样本语料个数约为30~60之间时,TSM-STM和STSM-HOSTM的分类精度都优于VSM-SVM,可达到70%以上。将TSM-STM和STSM-HOSTM的分类结果进行比较可以发现,当训练样本语料个数小于30时,TSM-STM的分类精度急剧下降,而STSM-HOSTM的分类精度略微下降,但仍保持着70%以上的准确率。 表4给出语料总数为200和400时,三种算法在训练样本与测试样本不同分配比例下得到的测试集分类准确率,对应于图6(a)和(b)的结果。 第二,固定训练集。3个二分类组各包含的语料总数为800,在固定训练集语料个数为20、40、60、80的四种情况下,将测试集语料个数从40增加至800,每次增加40个语料,对VSM-SVM、TSM-STM和STSM-HOSTM的分类性能进行比较,测试准确率为3个二分类组的平均值。实验结果见图6和表5。 表4 实验A分类结果比较表 图6 实验B结果比较图 表5 实验B分类结果比较表 图6表示训练集语料个数固定,测试集语料个数变化时,VSM-SVM、TSM-STM和 STSM-HOSTM对测试集的分类准确率曲线。其中实心圆点、空心圆点和实心方块曲线分别是VSM-SVM、TSM-STM和STSM-HOSTM的分类结果。图7(a)~(d)分别为训练集语料个数取20、40、60和80的分类结果。图7(a)和(b)表明,当训练集语料个数为20和40时,STSM-HOSTM的分类性能明显优于VSM-SVM和TSM-STM。相应的测试集分类准确率由表4给出。可以看到,训练集语料个数取20时,STSM-HOSTM的准确率均在70%以上,VSM-SVM和TSM-STM的准确率在55%附近波动,TSM-STM略优于VSM-SVM。当训练集语料个数取40时,STSM-HOSTM的准确率在测试集语料个数小于400时超过了80%,在测试集语料个数超过400时,准确率接近80%。而VSM-SVM和TSM-STM的分类准确率虽有所提高,但仍明显低于STSM-HOSTM。VSM-SVM与TSM-STM相比,TSM-STM的性能整体上优于VSM-SVM。图7(c)给出训练集语料个数取60的实验结果,可以看到随着训练语料的增加,VSM-SVM和TSM-STM的分类性能快速提升,此时TSM-STM的平均分类准确率已超过STSM-HOSTM。TSM-STM和STSM-HOSTM均优于VSM-SVM。从图7(d)看出,当训练集语料个数达到80时,VSM-SVM的分类准确率快速上升,达到90%以上,超过了TSM-STM和STSM-HOSTM。与训练集语料个数取60时的结果相比,TSM-STM和STSM-HOSTM的分类准确率略有上升。 实验A和实验B的分类结果均表明,当训练集语料个数小于60时,基于张量表示的TSM-STM和STSM-HOSTM的分类性能都显著的优于基于向量表示的VSM-SVM。这或许是因为,小样本训练语料提供的信息不够充分,不能使VSM-SVM得到充分训练,从而不能很好地识别文本特征,分类性能低下。而文本的张量表示蕴含着文本的结构特征,而这种潜在的结构特征有助于提升分类算法性能。前期关于基于TSM的文本分类的研究已表明,与基于VSM的文本分类相比,文本的张量表示更利于小样本训练集下的文本分类,上述实验结果正是对此结论的进一步验证[5-6]。 将STSM-HOSTM与TSM-STM的实验结果做进一步对比,可以看到,当训练集语料个数减少至30以下时,TSM-STM变的极不稳定,分类性能快速下降,而STSM-HOSTM的分类准确率却能稳定地保持在75%~80%之间。这说明在小样本情况下,向文本张量表示中加入的更为明确的文本层次结构信息能够起到保持分类算法稳定性、提高分类精度的作用。由此说明在文本的表示中加入有效的文本结构特征对提高后续文本处理任务的效果确实有着重要的意义。 2)实验B:复旦语料分类实验 为了验证的模型能够有更广的适用性,还在复旦语料下进行了文本分类的实验。在复旦语料中,我们分别在艺术与农业,农业与政治下进行了文本分类,并且固定语料的训练集为60个,不断增加测试集从40,80,…,400,测试不同测试集下分类模型对应的测试集的正确率。其结果见图7和表6。 (a)艺术与农业 (b) 农业与政治 图7 复旦语料下的分类实验图 表6 实验C分类结果比较表 图7中,(a)表示艺术与农业下的分类实验,(b)表示农业与政治下的分类实验,各个曲线和之前的实验相同。从(a)和表6中,可以看出VSM-SVM下的分类正确率均不高于80%,而STSM-HOSTM与TSM-STM的正确率均高于80%,相比较TSM-STM,STSM-HOSTM的正确率更高,大多数超过了88%,其曲线整体在另外二者的上方。从(b)和表6中可以发现,VSM-SVM的曲线程序上升趋势,但是其整体正确率仍然比较低,大多数实验组的正确率不高于80%。而TSM-STM与STSM-HOSTM的正确率均高于80%,其中TSM-STM的正确率在80%到90%区间段,曲线整体比较平稳;STSM-HOSTM的正确率大多数在90%以上,曲线于另外二者上方。 可以发现,当使用复旦中文语料时,STSM-HOSTM与TSM-STM两者的正确率均高于VSM-SVM的分类正确率,并且STSM-HOSTM的分类正确率效果相比较于另外两者是最好的。这再次验证了STSM-HOSTM在小样本数据下的优势。 本文提出一种新的文本表示模型——基于文本分层表示的结构张量空间模型(HR-STSM)。HR-STSM将文本表示为3阶张量,继承了2阶TSM的维度低的优点,并且包含了文本的层次结构信息。利用本文提出的文本层次结构提取算法(HSEA),能够实现文本的自动分层,从而得到文本的结构张量表示。与高阶支持张量机相结合得到的STSM-STM分类算法对小样本的分类任务具有显著的优势,分类性能明显优于VSM-SVM和TSM-STM。 当训练样本的数目足够大时,基于张量表示的 STSM-HOSTM和TSM-STM的分类性能的提升都不如VSM-SVM。这可能是由于随着样本量增大,分类器获得了充分训练,从而一方面弱化了文本结构信息对分类性能提升的影响;另一方面,TSM不能明确地表示文本的结构,而本文提出的HR-STSM可能会出现层次特征提取不够合理的问题,由此导致TSM-STM和STSM-HOSTM在大样本数据下性能不如VSM-SVM。 文本的层次结构提取是较为复杂的问题,类型和内容不同的文本可能具有不同的层次结构。一方面,在处理新闻语料分类问题时,本文仅是将所有语料的层次粗略地进行硬划分,使得同类别语料的相同层次之间的相关度不够显著;另一方面,在文本层次结构提取时仅使用了词频这个特征。因此,需要对文本的STSM表示开展进一步的研究:(1) 结合其它文本处理技术和文本语义信息,提取语义结构更明确的文本层次表示模型;(2) 探索文本的其它结构表示形式及提取方法;(3) 研究STSM表示下的张量分类算法;(4) STSM在其它文本处理任务中的应用研究。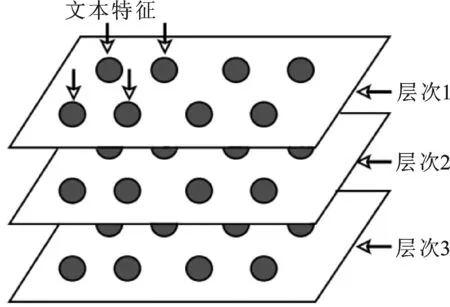
三、基于STSM的文本分类
(一) STM分类模型的一般形式
(二)基于交替优化的高阶STM学习算法
四、实验结果与分析
(一)实验环境
(二)实验语料


(三)实验结果分析





五、结束语
