模糊分数阶PID在线径控制系统中的应用
2019-07-26周克良胡梁眉洪智慧
周克良,胡梁眉,洪智慧
(江西理工大学 电气工程与自动化学院,赣州 341000)
0 引言
在电线电缆的生产过程中,绝缘挤出是最主要的工序之一,而推挤机则是完成这一过程的主要设备,其原理是将绝缘材料PTFE挤出到金属丝上完成绝缘挤出工序。在绝缘挤出过程中,主要技术要求有偏心度、光滑度和致密度,其中偏心度是最能体现挤出工艺水平的重要指标,它代表了挤出的绝缘厚度的偏差值,决定了线径(电缆外径),故以线径作为衡量控制器的重要指标。线径控制系统具有时变性、非线性、大滞后等特点。目前,传统的PID控制策略以其结构简单、控制效果及稳定性好、易于操作等优点在线径控制系统中应用广泛,但由于PID参数始终不变,在具有滞后特性的线径控制系统中很难达到最理想的效果。针对线径控制滞后大这一控制问题,最早是在2006年有学者[1]提出了一种带有滞后补偿的优化模糊PID算法,加快了响应速度,减轻了系统振荡,但抗干扰能力有待提高。之后在2009年[2]提出了动态矩阵控制算法,该算法对未来时刻过程的响应趋势进行预测,使得系统输出能尽可能好地跟踪期望值,但调节时间较长。最新的研究成果是在2017年,学者Hui Li[3]等人设计了基于蚁群优化算法(ACO)的ACO-KF-PID算法,并引入卡尔曼滤波算法,以抑制控制扰动和测量噪声对线径控制系统的影响,实现了电线绝缘护套挤出成型的智能化控制。
模糊PID控制是将模糊控制与PID控制相结合的一种复合控制方式,虽然该方式弥补了PID控制容易使闭环迟钝,易产生振荡的缺点,但超调较大。再结合分数阶微积分理论,在模糊PID控制器的基础上,对其微分阶次及积分阶次进行从整数阶到非整数阶的拓展,构成模糊分数阶PID控制器(FOFPID),以误差和误差变化率作为输入信号,利用模糊控制规则对KP、KI、KD、λ和μ五个参数进行在线调节。与模糊PID控制器相比,该控制器增加了调节参数的个数,使得控制器的控制范围更大、更灵活。并利用Smith预估器对纯滞后对象的有效补偿,在实践中获得了满意的控制效果。
近年来,学者们对模糊分数阶PID控制器的应用研究[4~9]验证了模糊分数阶PID控制器具有较好的动态性能和抗干扰能力。故在本文中,针对推挤机系统的线径控制问题,设计出带滞后补偿的FOFPID控制器,对推挤机的推挤速度进行控制,提高电缆外径控制精度,满足实际生产需求。同时结合ITAE指标,利用SIMULINK仿真对模糊PID控制器、动态矩阵控制算法及带滞后补偿的FOFPID控制器的控制效果进行比较。
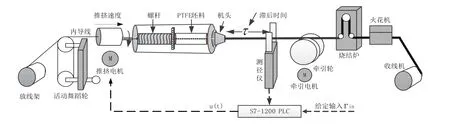
图1 线缆生产工艺流程图
1 线径控制系统的结构
在电缆生产的绝缘挤出工程中,放线架在牵引电机的作用下匀速放线,在内导线经过机头时,采用螺纹装置为活塞提供推力,将PTFE(聚四氟乙烯)材料挤出,使之在金属线芯的表面形成一层厚度均匀的绝缘外皮,由机头与牵引电机之间的测径仪对吸附绝缘外皮后的金属线芯的直径进行测量[10]。之后的烧结炉会将分散的聚四氟乙烯颗粒通过烧结作用凝聚成一个没有缝隙的整体[11]。最后,成形的电缆将受到工频火花机的检验,一旦线缆存在纵向开裂问题,将会被火花机击穿,能够及时将不合格的线缆剔除。线缆生产工艺流程如图1所示。
线缆的线径主要取决于推挤机的推挤速度和牵引速度,故若要使线径保持稳定,可从推挤速度和牵引速度这两方面来分析。在对线径控制系统进行设计时,保持推挤机的牵引速度不变,通过对推挤机的推挤速度进行有效控制,实现对电线电缆生产工艺的优化。推挤速度越大,线径则越大;推挤速度越小,线径则越小。
线径控制系统采用西门子PLC S7-1200作为控制器,电缆外径通过外径测径仪传递给PLC,由于机头与外径测径仪之间有一定的距离,这使得此系统对输入的响应具有滞后性,可用一阶惯性加纯滞后环节等效,螺杆调速系统为直流闭环调速,模型可等效为二阶惯性环节。其模型[1]可表示为:
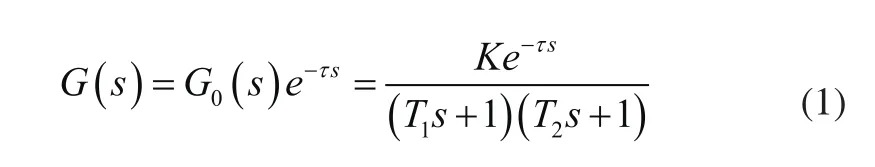
其中G0(s)为系统无滞后下的传递函数,K为放大倍数,T1、T2分别为大、小惯性时间常数,τ为滞后时间常数。根据相关研究成果[1~3]并结合现场推挤机设备WE-LIN040LS-2.0以及实验数据,可得到适合线径控制系统模拟的传递函数为:

PLC将实时根据测得的线径与目标线径的偏差及偏差的变化率,对推挤直流电机驱动器的输入电压进行控制,实现对推挤速度的调节,使得生产的线缆线径紧紧能够跟随目标线径。线径控制系统结构图如图2所示。图中rin为目标线径,y(t)为实际线径。

图2 线径控制系统结构图
2 基于FOFPID 的线径控制方案设计
2.1 分数阶PID控制器的结构
PIλDμ控制器是一种新型的控制器,它与传统PID控制器相比,分别对积分系数和微分系数增加了阶次调节参数λ和μ,因而它具有更大的调节范围[12,13],PIλDμ控制器可表示为:

分数阶PID控制系统结构示意图如图3所示。

图3 分数阶PID控制系统结构示意图
2.2 基于FOFPID控制器的线径控制方案
推挤机系统是一个复杂的不稳定系统,两根胚料接头处存在间隙或者胚料存在断裂等情况都将使得系统不稳定,线径波动较大,这些情况可以看成是某个扰动信号。针对推挤机系统的这些特点,结合Smith预估器的性质,设计出带滞后补偿的FOFPID控制器的线径控制系统框图,如图4所示。

图4 带滞后补偿的FOFPID控制器的线径控制系统框图
带滞后补偿的FOFPID控制器设计大致可分两步:FOFPID控制器设计和Smith预估器设计。其中FOFPID控制器的设计又由两部分组成,以线径的误差e和误差变化率ec作为控制器输入,经模糊推理后的解模糊分别输出分数阶PID控制器参数的增量△KP、△KI、△KD、及微分阶次λ和微分阶次μ。其中,前者的模糊规则可根据工程设计人员的技术知识和实际操作经验建立,后者的模糊规则通过比较不同的λ和μ在线径控制系统中对控制效果的影响来建立。
3 带滞后补偿的FOFPID 控制器的设计
3.1 FOFPID控制器的设计
在上述FOFPID控制器中,输入e和ec,输出△KP、△KI、△KD、λ和μ的模糊集均为{BN,MN,SN,OZ,SP,MP,BP}, 分别表示“负大值”、“负中值”、“负小值”、“零值”、“正小值”、“正中值”、“正大值”。
3.1.1 基于KP'、KI'、KD'的模糊规则
由于线径控制系统需要系统在响应初期具有较好的快速跟踪性能,且响应过程中不出现过大的超调 ,且应避免系统在进入稳态调节阶段后在设定值附近出现震荡。根据这些要求,先选取KP、KI、KD的初值,并将其送入FOFPID控制器中,对△KP、△KI、△KD进行参数整定,得到实时的自适应的PID控制参数KP'、KI'、KD'。

比例系数KP'的作用是加快系统的响应速度,提升系统的调节精度。KP'越大,系统的响应越迅速,调节精度越高,但易产生超调,影响系统稳定性;积分系数KI'的作用是减小系统的稳态误差。KI'越大,越易消除系统的稳态误差,但KI'过大,在响应过程的初期会产生积分饱和现象;微分系数KD'的作用是改善系统的动态性能。但KD'过大,会延长调节时间,降低系统的抗干扰能力。根据KP'、KI'、KD'的性质,再结合工程设计人员的技术知识和实际操作经验,建立合适的模糊规则,针对△KP、△KI、△KD的模糊规则分别如表1、表2、表3所示。其中,△KP、△KI、△KD的论域如下:△KP={-0.25,0.25}、△KI={-0.06,0.06}、△KD={-3,3},e、ec和△KD采用相同的隶属度函数相同,各参数的隶属函数[14,15]如图5所示。
在本文中,选取KP、KI、KD的初值为KP=1、KI=1、KD=1。
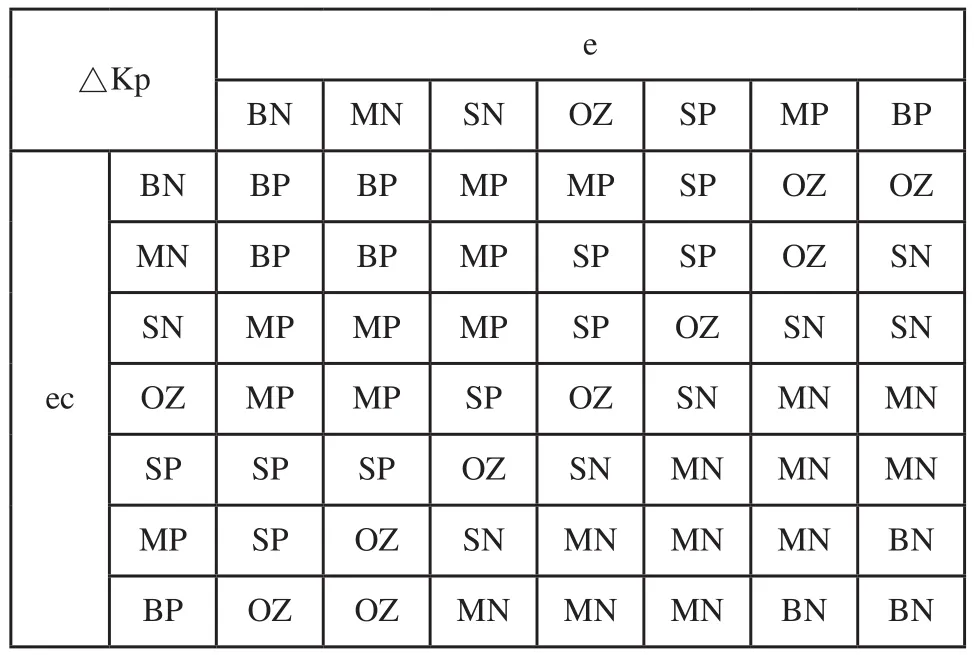
表1 △KP模糊控制规则表

表2 △KI模糊控制规则表

表3 △KD模糊控制规则表
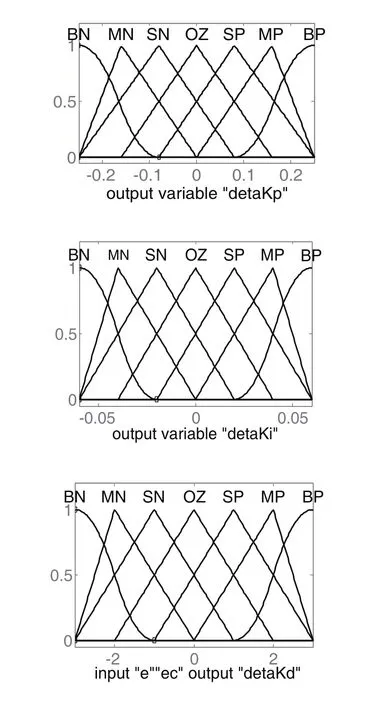
图5 隶属函数图
3.1.2 λ、μ在线径系统对线径控制效果的影响
在MATLAB仿真中,分别对λ、μ取不同的值进行分析,观察其对阶跃响应的影响。
1)线径系统中不同积分阶次对控制效果的影响
在仿真中:固定μ=0.8,分别选取λ=0.8、λ=0.67、λ=0.45、λ=0.37做四组仿真实验,结果如图6所示。随着λ的增大可以看出系统的响应速度加快,但超调也越来越大。当λ=0.37时,虽然没有超调,但始终没能到达稳态;当λ=0.8时,超调过大。可从图中看出当λ=0.45时,系统综合表现较好,超调较小,在10秒时系统已经接近稳定。故可以认为在线径控制系统中λ对超调量的影响较大,且在λ=0.45附近可以很好的控制系统的超调,稳态误差较小,过渡时间短。
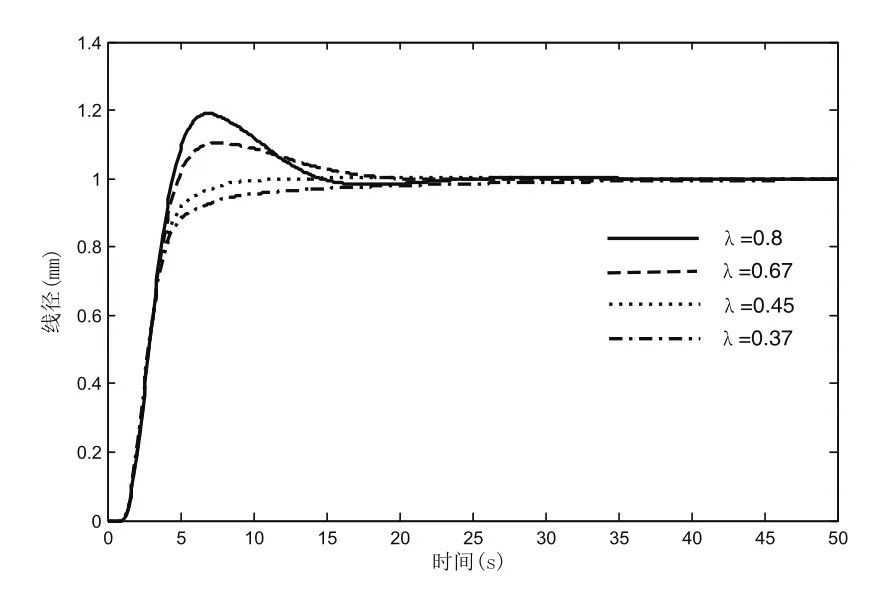
图6 不同微分阶次下的阶跃响应
2)线径系统中不同微分阶次对控制效果的影响
在仿真中:固定λ=0.45,分别选取μ=0.9、μ=0.65、μ=0.45、μ=0.37做四组仿真实验,结果如图7所示。随着μ的增大可以看出系统的震荡越来越小,但过渡时间略略有所加长。
当μ=0.37时,系统震荡特别剧烈,超调也比较大;当μ=0.65时,超调减小,曲线也相对平稳,但仍然存在些细小的震荡;直至μ=0.9,系统不再出现震荡,超调较小,在9秒时系统已经接近稳定。故可以认为在线径控制系统中μ对稳态误差的影响较大,且在μ=0.9附近可以很好的控制系统的稳态误差。

图7 不同积分阶次下的阶跃响应
通过对λ和μ的研究,发现λ对超调量的影响较大,选择合适的λ可以有效减小系统的超调;而μ对稳态误差的影响较大,其主要作用是减小系统的稳态误差。在分数阶的系统中存在一个范围使系统的稳定性较好,所以找出线径控制系统中分数阶的稳定域是十分必要的。同时发现只有当λ和μ两个参数匹配时,能能取得较优的控制结果。
3.1.3 λ、μ模糊规则的建立
根据上文中的结论,再结合实际操作经验,得到针对λ和μ两个参数调整的模糊规则如表4所示。λ和μ的论域如下:λ={0,1.7}和μ={0,1.3},采用的隶属度函数如图8所示。

图8 隶属函数图
3.2 Smith预估器的设计
Smith[16~18]预估器通过对控制对象动态特性的估计,在传统负反馈结构的基础上引入补偿环节,使延迟了的被调量提前反映到调节器使之动作,从而消除滞后环节对系统的影响,降低了滞后环节对整个控制系统造成的影响,提高了系统的响应速度和稳定性。其控制结构如图9所示。

图9 Smith预估器原理图
4 系统仿真及结果分析
根据带滞后补偿的FOFPID控制器的控制原理在MATLAB的SIMULINK中建立仿真模型,如图10所示。微分时间和积分时间的分数阶运算均采用MATLAB Function来建立。在SIMULINK中进行仿真时,线径设定值为某通讯线缆生产设定值3.58mm,与相同参数的模糊PID控制器及文献[2]中的动态矩阵控制器进行对比。
4.1 阶跃响应和抗干扰分析
在仿真时,为比较不同控制方法的抗干扰能力,30s处加入了一个阶跃值为-1.5的阶跃扰动信号,实验结果如图11所示。
由图11的实验结果可见,在对具有时变性、非线性、大滞后性质的线径控制系统进行控制时,前30秒系统未受到外界扰动,采用模糊PID控制器,系统超调量%约为25.7%,调节时间ts约为17s,线径波动较大,调节时间较长;采用动态矩阵控制器,系统超调量σ%约为6.1%,调节时间ts约为12s,与模糊PID控制相比线径波动更小;采用带滞后补偿的FOFPID控制器,虽然响应速度较慢,但系统几乎无超调,调节时间约为8s,线径波动较小,调节时间较短。当系统受到外界扰动时,带滞后补偿的FOFPID控制器的曲线响应速度较快,波动较小,而模糊PID控制和动态矩阵的曲线响应速度较慢,波动较大。
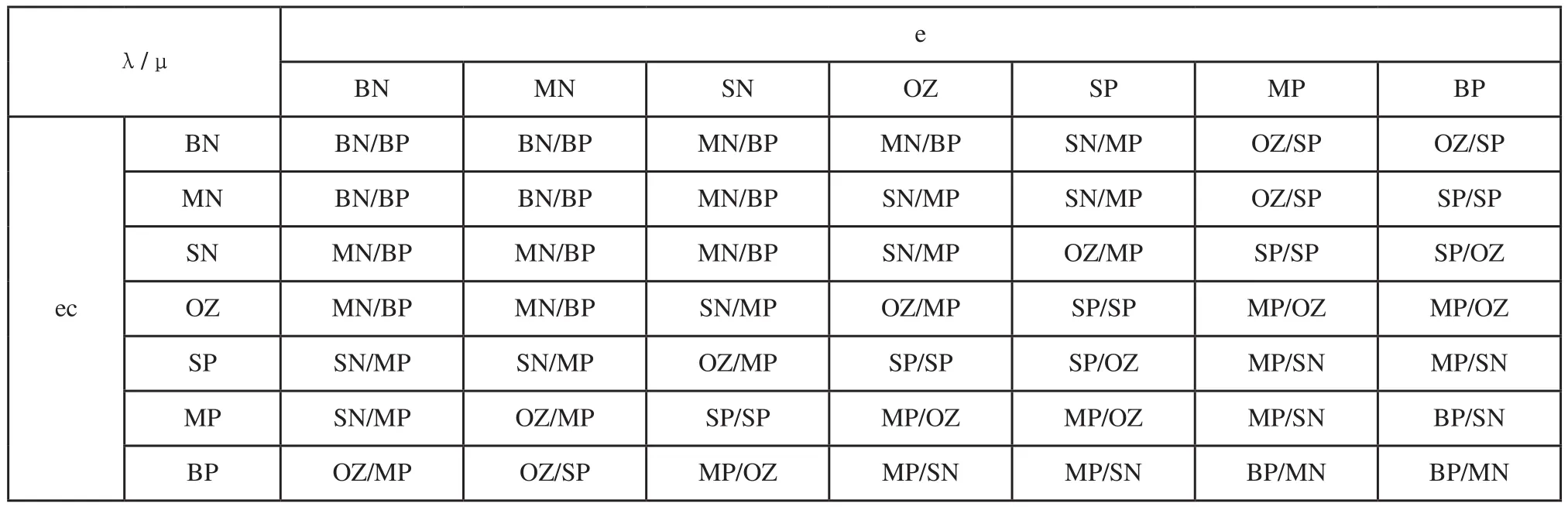
表4 γ、μ模糊控制规则表

图10 SIMULINK仿真图

图11 加扰动信号的仿真曲线
4.2 系统鲁棒性分析
将系统纯滞后时间常数增大50%、将线径设定值改变为3mm,观察系统的阶跃和扰动响应曲线变化情况,对滞后时间变化的鲁棒性进行分析,实验结果如图12所示。

图12 增大滞后时间的仿真曲线
由图12曲线可知,当系统滞后时间增大后,模糊PID控制的超调量没写增加,且产生了震荡。动态矩阵控制的超调量虽然有所增加,但调节时间变化不大,整个过渡过程相对比较缓和,且系统仍然是稳定的,说明动态矩阵具有比较强的鲁棒性。而带滞后补偿的FOFPID控制器受滞后时间变化影响最小,仍能保证良好的控制效果。
4.3 ITAE判据分析
在本文中采用ITAE判据[19]对模糊PID控制器、动态矩阵控制器及带滞后补偿的FOFPID控制器进行分析与评价。ITAE是时间乘以误差绝对值积分的性能指标,它是以控制系统瞬时误差函数e(t)为泛函的积分评价,ITAE指标的值越小,代表着该控制系统越稳定,其定义如式(5)所示。

式中:T为仿真时间,|e(t)|为响应过程中的误差绝对值。
三种控制算法的ITAE指标值如表5所示。从表中可得出在增加扰动和加大滞后时间的情况下,带滞后补偿的FOFPID控制器较优于模糊PID控制器及动态矩阵控制器。

表5 三种方案下ITAE性能指标对比
5 结束语
针对PTFE推挤机线径控制系统的时变性,非线性,大滞后等特点,本文提出了带滞后补偿的适用于推挤机线径控制系统的FOFPID控制算法,并在MATLAB的SIMULINK中对三种控制算法的阶跃响应进行分析比较。结果表明,带滞后补偿的FOFPID控制器的控制效果优于其他两种算法。系统能够实现线缆线径在目标线径附近小范围波动,有较好的快速响应能力及抗干扰能力,满足线缆实际生产需求,有一定的推广价值。
