车间多行布局精准建模与多目标优化研究

徐修立，沈梦超，陈浩杰，张 剑

（西南交通大学 先进设计与制造技术研究所，成都 610031）

0 引言

随着市场竞争的日趋激烈化，要求企业对生产车间进行精准或者重构布局，以适应市场的快速变化，因此车间布局及优化问题成为了制造领域重要研究课题之一[1]。据统计，一个企业车间的物料搬运费用约为制造总成本的20%～50%，而优化车间布局能减少搬运量、搬运距离和等待时间，使物流成本至少降低10%～30%[2]。

车间布局问题是指将机床设备及其辅助设施在给定的空间内进行布局，并且满足相应的约束条件，通过优化以获取最佳目标函数值[3]。目前，在车间布局问题中建立的数学模型主要包括二次分配模型、混合整数规划模型、二次集合覆盖模型、线性多行直线布局模型等[4]。在车间布局模型求解方面，已广泛采用启发式优化算法[5]。如郭源源[6]将粒子群算法与经典的系统布置设计法相结合来求解面向车间布局的连续空间优化问题，Kulturel-Konak[7]提出了一种混合粒子群算法来求解不等面积的车间布局问题，Pourhassan[8]提出了采用非支配排序遗传算法（NSGA-II）求解多目标动态设施布局优化问题。由于遗传算法操作简单、且具备鲁棒性，文献[9～11]等均采用遗传算法或其改进来对车间布局问题进行优化求解。

建立车间布局数学模型是一个化繁为简的过程，但过于简化往往导致数学模型与实际物理模型之间存在较大的差异。例如布局时不等面积功能区横纵向放置问题、竖向主干道、行距可变等实际情况被忽略，同时优化的目标通常是物料搬运成本最小化的单目标，而忽略了车间的面积利用率等因素的影响。因此本文基于当前车间布局中较为常用的线性多行直线布局模型，充分考虑车间各种实际约束，建立更为精准的车间总体布局多目标优化数学模型，同时采用求解更为有效的多种群遗传算法，实现精准布局模型的求解，并将该方法应用于实例中说明其可行性与优越性。

1 车间总体布局精准数学模型的建立

采用多层次式布局策略[12]，对已经划分布置好的N个不等面积功能区进行车间总体布局，可以减少计算规模。根据车间现场的多重约束和规则，建立精准数学模型，构建多目标优化函数并求解，实现车间中总的物料搬运成本最低、车间面积利用率最大等目标，以便得到最优车间布局解。

1.1 模型假设与符号说明

本文采用线性多行直线布局模型对车间进行总体布局。考虑实际厂房的空间约束，而功能区单元布置行数未知，故采用自动换行策略。为便于建模和提高计算效率，对多行直线布局做出如下假设：1）待布局的车间为二维平面，且是长宽大小已知的矩形；2）待布置的功能区均为长、宽已知的矩形，忽略其高度；3）各功能区分行排列，且平行于车间长宽方向，即平行于x轴和y轴；4）排列在同一行的功能区其中心点在同一条水平线上。

车间与功能区的几何模型如图1所示。

图1 线性多行设备功能区布局示意图

其中L、W分别表示待布局车间的长度和宽度，Ai表示功能区单元i，xi表示i功能区的x轴方向坐标，yi表示i功能区的y轴方向坐标，li表示i功能区的长度，bi表示i功能区的宽度，hik表示i功能区和k功能区之间的横向最小安全距离，Δi表示i功能区和k功能区之间的净间距，s0表示第一行功能区与车间边界设定的距离，Sm,m-1表示两相邻行之间的行距，hj0表示j功能区与车间边界的最小安全距离，yn表示n功能区所在行的y轴方向坐标位置值大小。

1.2 优化目标

本文以车间总物料搬运成本最小和面积利用率最大为优化目标建立多目标精准数学模型，以满足物流原则和布局紧凑原则。

1）车间中总的物料搬运成本最小化

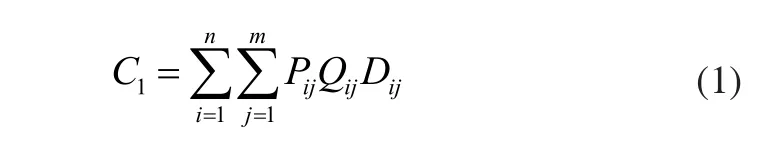
式中：Pij为功能区i和功能区j之间的单位物料在每单位距离之间进行搬运所需的费用，Qij为功能区i和功能区j之间的物料搬运频率，m为车间总体布局后的总行数，n为功能区的总数量，Dij为功能区i和功能区j之间的矩形距离，其公式如下：

2）车间面积利用率最大化

面积利用率最大问题可以转化为布局结果所包络功能区的矩形面积St最小问题，St的计算公式如式(3)所示：

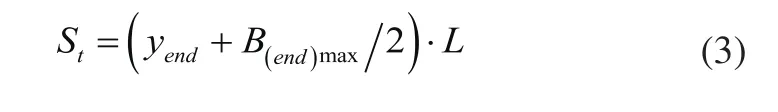
布局过程采用自动换行策略，其中yend为布置在车间最后一行功能区的纵坐标，B(end)max为最后一行功能区中宽度最大的功能区宽度尺寸。由此该目标函数的表达式为：

根据优化目标之间的相对重要程度，采用加权法构造新的优化目标函数，将多目标优化问题转换为单目标优化问题进行求解：

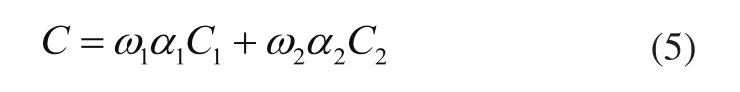
式中：ω1、ω2为加权因子，且满足ω1+ω2=1，α1、α2为归一化因子。

1.3 精准数学模型约束条件

建立车间布局精准数学模型的约束条件如下：

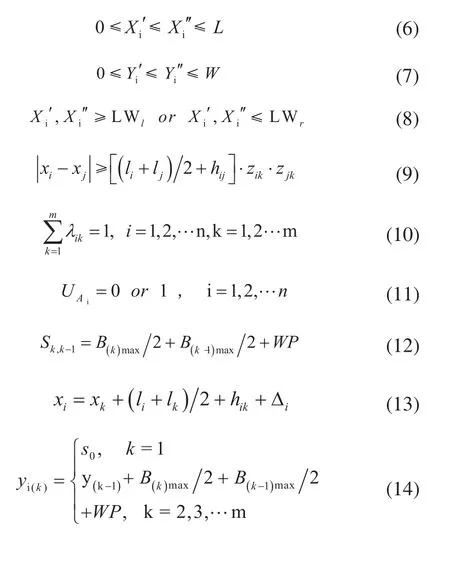
式中：（Xi'，Yi'）、（Xi''，Yi''）分别为矩形功能区i的左下角和右上角的坐标；LWl、LWr分别表示竖向主干道沿x轴方向的左、右两边的坐标大小；决策变量Zik=1表示功能区i在第k行上，否则Zik=0；决策变量UAi=0表示功能区i横向放置，UAi=1表示功能区i竖向放置；B(k)max为第k行功能区中宽度最大的功能区宽度尺寸；yi(k)表示功能区i的y轴方向坐标（功能区i位于第k行），y(k-1)表示第k-1行的y坐标大小，WP表示设定横向主干道的尺寸大小，一般不设定横向主干道则WP=0。

式(6)、式(7)表示功能区的横纵坐标方向不超过车间最大长度和最大宽度，式(8)保证功能区布局避开竖向主干道，式(9)保证同一行的功能区不能重叠且满足其安全距离，式(10)保证一个功能区在布局中只能出现一次，式(11)表示功能区可横向、竖向选择放置，式(12)表示设置自适应行距：即布置有功能区的任意相邻两行k行、k-1行的行距可根据所布置的功能区尺寸大小自适应确定行距大小，而非采用固定行距约束要求：根据所有功能区中最宽功能区的宽度设置每相邻两行行距为定值大小[13]，式(13)、式(14)分别表示功能区矩心的横（x轴）、纵（y轴）坐标求解公式。

2 改进多种群遗传算法求解

遗传算法是模拟生物进化过程搜索最优解的方法，具备很强的全局搜索能力和鲁棒性，但是也存在早熟收敛和收敛性能差等缺陷与不足[14]。为此，本文采用一种改进多种群遗传算法（MPGA）对车间总体布局问题进行优化求解，该算法通过模拟自然生态系统协同进化，具有全局、局部搜索能力强和收敛精度高等特点[15]。

2.1 改进多种群遗传算法流程

多种群遗传算法流程如图2所示，具体操作过程如下：

Step1：随机产生N个初始种群，每个种群的规模大小为M，初始化种群并计算个体的目标函数值。

Step2：利用2.2节中设计的交叉和变异概率参数控制式(15)、式(16)对每个种群分别设定不同的交叉和变异概率控制参数。

Step3：N个种群各自独立进行标准遗传算法（simple genetic algorithm，SGA）的选择、交叉、变异等操作。

Step4：采用移民算子交换种群间信息。

Step5：利用人工选择算子选出每个种群的最优个体保存至精华种群中。精华种群不进行选择、交叉、变异等遗传操作，保证迭代过程中不破坏和丢失最优个体。

Step6：判断精华种群中的最优个体最少保持代数是否达到设定的最大保持代数，若是，则寻优过程结束，输出最优解；否，则继续循环迭代。

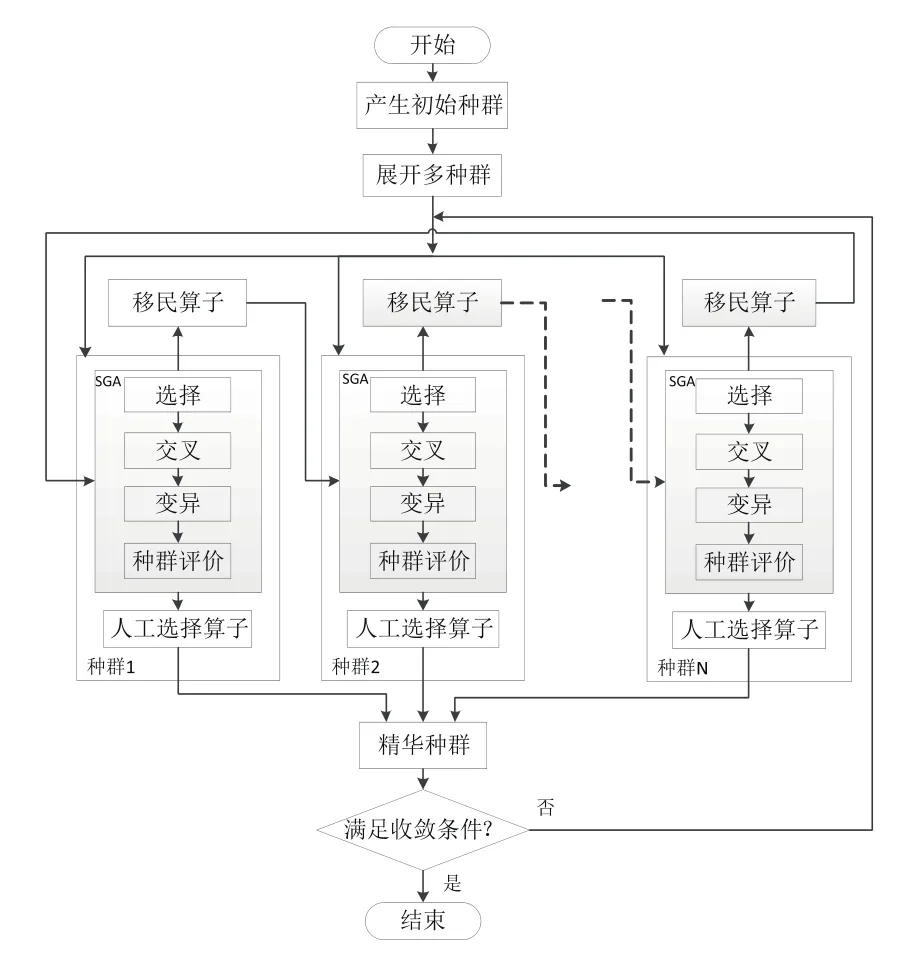
图2 多种群遗传算法（MPGA）流程示意图

2.2 交叉和变异概率参数控制公式设计

遗传算法中交叉概率和变异概率的参数设置决定了全局和局部搜索能力，若按传统多种群遗传算法的操作，对每个种群设定相同的交叉概率Pc和变异概率Pm，会存在交叉、变异概率设置不合理致使多种群遗传算法陷入早熟收敛的问题。故本文通过设计交叉和变异概率参数控制公式给予每个种群不同的控制参数，则不同种群以不同的交叉和变异概率协同进化，兼顾了算法的全局和局部搜索，降低了算法求解陷入局部最优的可能性，提高了多种群遗传算法的收敛精度。结合交叉概率取值范围（pcmin，pcmax）和变异概率取值范围（pmmin，pmmax），设计交叉和变异概率参数控制公式：

其中，randN（0，1）为在0～1区间产生的随机数，有N个种群则分别产生N个0～1之间的随机数值。

2.3 多种群遗传算法设计

2.2.1 基因的编码

基因编码方式由功能区排列顺序、净间距和功能区单元横竖放置选择三部分构成，采用混合的编码结构，表达方式为：[{A1，A2，…，An}{Δ1，Δ2，…，Δn}{0，1，0，0，1，...}]。其中：功能区排序时采用整数编码，Ai为功能区，其顺序为功能区i的排列顺序；净间距采用实数编码，Δi为功能区i和功能区i-1或边界之间的净间距；功能区单元横竖放置选择采用二进制编码，1表示功能区单元竖向放置，0表示功能区单元横向放置。

2.3.2 种群评价函数

根据1.3节中式(13)、式(14)求出该染色体序列每个功能区的x、y坐标；根据1.2节中式(5)求出加权后的多目标优化函数值C，由于所求目标为极小值，故而适应度函数设为：

其中：f为适应值；T为罚函数，使得不满足约束条件的较差个体具有较低适应度值。

2.3.3 遗传算子

选择操作采用轮盘赌的方式，各种群采用文献[16]中标准遗传算法（simple genetic algorithm，SGA）的交叉、变异操作。

2.3.4 算法终止条件

与标准遗传算法（SGA）中人为设定最大终止迭代次数不同，本文算法通过判断当精华种群中的最优个体连续保持代数达到设定的保持代数时，则算法终止，输出最优解。避免因设定迭代次数不合理而导致算法在收敛前过早结束或收敛后浪费计算资源的情况。

2.4 移民算子

由于各种群是相对独立的，故本文通过引入移民算子将其联系起来。移民算子是将迭代过程中各种群里的最优个体定期的交换至其他种群，从而实现种群间的信息交换，交换的染色体作为外来优秀个体引入，避免了迭代进化后期因种群多样性降低致使算法陷入局部最优。移民算子具体操作为：将目标种群中的最差个体用其他种群中的最优个体替换，即将N个种群编号（1，2，…，r，…，N），种群r中的最差个体由种群r+1中的最优个体代替，以此类推，种群1中的最差个体由种群N中的最优个体代替，完成移民操作。

2.5 参数设置

本文分别采用SGA算法和MPGA算法对目标函数进行求解，取加权因子ω1=0.6，ω2=0.4。SGA算法：M=50，Pc=0.8，Pm=0.08，设定终止判据：最大迭代次数为200代；MPGA算法：N=10，M=50，设定Pc取值范围（0.6,0.9）和Pm取值范围（0.01,0.1），设定终止判据：最优个体最少保持代数为5代。

3 实例验证及分析

某制造企业准备建新厂房，长90米，宽60米，考虑在厂房长度方向中间位置处设置一条4米宽的竖向主干道。企业确定了未来五年生产所需设备的类型及数量，同时基于成组技术，对设备进行了功能区单元的构建，功能区划分构建结果如表1所示。根据零件加工工艺和功能区构建结果，分析物流情况可获取从至表，同时设置安全距离。

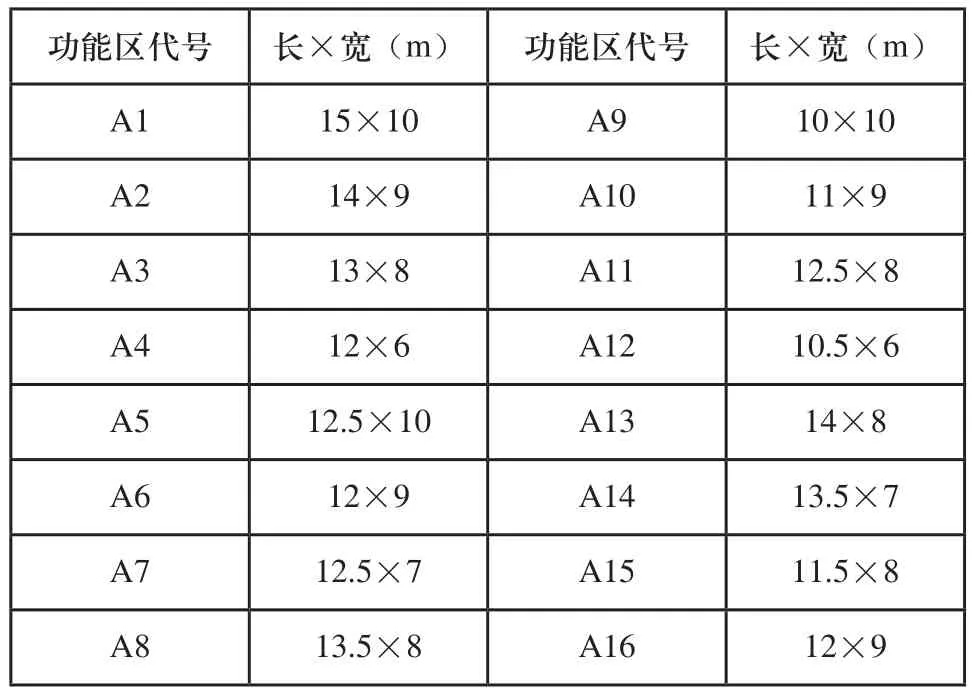
表1 功能区信息表

采用上文的相关参数设置，设计了如表2中的6组实验；并且根据不同实验方案，运用Matlab软件编写了相应程序。每种实验方案均运行10次，取其中最优解及目标函数的平均值作为数据结果如表3所示；为了比较算法性能，实验1与实验2同时迭代到200代的进化结果对比如图4所示。

表2 实验方案表

表3 优化数据结果对比表

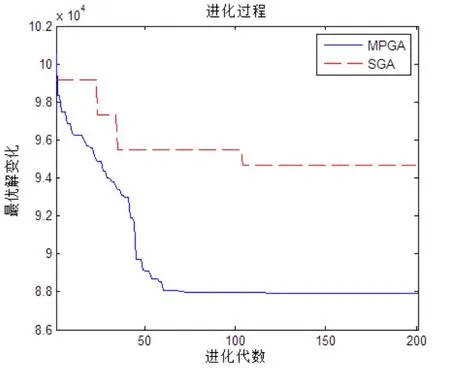
图3 MPGA与SGA进化迭代结果对比图

结果分析：对比表3中实验1和实验2的数据结果，采用多种群遗传算法（MPGA）比采用标准遗传算法（SGA）求解的目标函数值小5%，同时从图3中MPGA与SGA进化迭代结果对比可见，SGA在进化到100代左右即陷入了局部最优解，采用MPGA算法求解的精度明显比SGA求解精度更高。

对比实验2和实验5的优化数据结果，采用自适应行距得出的布局结果会比采用固定行距约束结果更优，其总物流成本降低了3%，面积利用率提高了6%。

对比实验2和实验6的数据结果，考虑功能区横竖放置的最优解精度可提高3%，更容易得到车间布局最优解。

对比实验2、实验3（在实验2布局结果中强行加入竖向主干道）和实验4的优化结果说明，在不考虑竖向主干道进行优化时，虽然简化后的优化模型得到目标函数值是这3个实验中最小的，但是真正加入竖向主干道后，实际目标值却增大9%，说明在建立数学模型时应考虑竖向主干道的实际约束，从而更能求得符合实际车间布局的最优解。故本文实例最终采取实验4方案，最大化地减小了物流成本且提高了面积利用率，求解所得布局结果示意图如图4所示。

图4 车间布局方案示意图

4 结论

本文改进了多行直线布局模型中行与行之间固定行距的约束，给出自适应行距约束定义，使布局面积更小、物流成本更低。同时针对目前车间总体布局数学模型过于简化的缺陷，在优化数学模型中加入了功能区单元横竖选择放置及竖向通道设置，建立了更为符合车间实际布局情况的精准数学模型。采用改进多种群遗传算法（MPGA）对该数学模型进行多目标优化求解，通过设计交叉和变异概率参数控制公式，使群体保持多样性，采用移民算子联系种群，降低了算法求解陷入局部最优的可能性，提高了多种群遗传算法的收敛精度，最后通过实例验证了所建模型的实用性和所用算法的优越性。