云仿真平台任务负载均衡优化调度研究
2019-07-26金鹏
金 鹏
(辽宁工程职业学院 信息中心,铁岭 112008)
0 引言
在工程及制造行业中,通常利用大型CAE软件进行工程数值分析、结构与过程优化设计、强度与寿命评估、运动、动力学仿真,以此验证未来工程、产品的可用性与可靠性[1]。随着设计模型越来越复杂,网格划分越来越精细,单机版的CAE软件运行效率低下,无法满足系统计算要求[2]。当前,为提高仿真效率,通常需要通过多台服务器搭建云仿真平台,利用CAE并行模块将仿真任务分割为若干个并行子任务,再根据任务调度算法将这些子任务分配到多个虚拟计算资源节点同时并行仿真,利用云仿真平台高速的并行运算速度完成仿真分析。
不同的任务调度算法都会对仿真任务的执行时间和仿真系统的负载平衡造成不同的影响,进而影响云仿真平台的性能。当前,云仿真任务调度算法已成为云仿真的一个研究重点与热点[1]。
求解云仿真任务最优调度方案就是寻找云仿真子任务与云平台虚拟机的最优组合匹配关系。当前云仿真任务调度算法的研究大多先采用连续空间的智能优化算法(粒子群、蚁群、遗传等算法)求解调度方案,再对解值向量中的编码进行取整求余后得到十进制编码,如文献[3,4]。这种近似编码势必降低结果的精确度。
本文根虚拟机与子任务的两种组合关系为“匹配”与“不匹配”,用编码“1”代表“匹配”,编码“0”代表“不匹配”。将云平台中所有子任务与虚拟机的组合关系构造为离散二进制粒子群,利用混沌离散粒子群算法(CBPSO)搜索子任务与虚拟机的最优组合,即满足使适应度达到全局最优值,且各子任务与虚拟机匹配关系都为“1”。
1 负载均衡调度原理
云仿真平台的调度分为两个层次,第一个层次是任务调度,将负载过重虚拟机上的子任务动态调度到负载较轻的虚拟机上,使云平台的虚拟机集群整体上负载均衡;第二个层次是虚拟机调度,将负载过重物理主机上的虚拟机迁移到负载较轻的物理主机[3]。本文主要研究的是第一个层次的调度问题,即求解云仿真任务的最优调度方案。求解云仿真任务最优调度方案就是寻找云平台上的m个虚拟机与n个子任务(m<n)的最优组合匹配关系。
2 负载均衡调度模型
为保证云平台的性能及稳定性,又保证仿真用户的仿真效率需求,本文将综合任务总执行时间和负载均衡度建立总的适应度函数Fitness,在解集空间内,利用混沌离散粒子群算法(CBPSO)搜寻使Fitness达到最大值的最优位置,即当前云平台中虚拟机与仿真子任务为最优组合。
2.1 云仿真任务总执行时间
设当前云仿真平台中,仿真子任务Wj的长度为lengthi,虚拟机VMi的CPU运行速度为mipsi,则Wj在VMi上的执行时间timeij为:

其中,1≤i≤m,1≤j≤n,m和n分别是云仿真平台上虚拟机总数和仿真任务总数。
设分配到VMi的子任务(1个或多个)集合为k,则分配到节点V Mi上的所有子任务的执行时间为由于所有子任务并行运算,则当前云仿真任务总的执行时间为:

2.2 虚拟机集群负载均衡度
本文将虚拟机集群总体负载度的标准差作为虚拟机集群的负载均衡度。
设当前虚拟机VMi所能提供配置资源:

其中,mipsi为VMi的CPU处理速度;memi为VMi的内存大小;bwi为VMi网络带宽。
设当前VMi上的子任务所占用的配置资源:

则当前虚拟机VMi的负载度表示为:

其中,μ1+μ2+μ3=1,μ1、μ2、μ3分别为虚拟机VMi的CPU权重、内存权重、网络带宽权重,本文取μ1=0.6,μ2=0.3,μ3=0.1。
当前云平台虚拟机集群的负载均衡度可表示成:
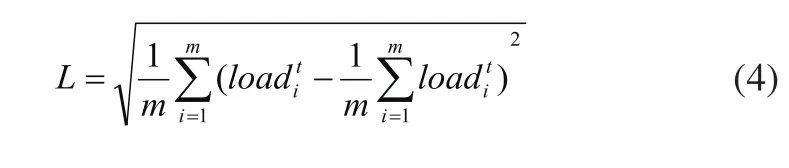
其中,m为云平台虚拟机数量。
可见,L越小,说明各虚拟机的负载波动越小,负载均衡性越好。
2.3 适应度函数
结合式(3)、式(4),归一化处理后建立以下适应度函数:

其中,Tmax,Tmin分别为子任务总执行时间的最大值与最小值,Lmax,Lmin分别为虚拟机集群负载均衡度的最大值与最小值;α为执行时间权重,β为负载均衡度权重,且满足α+β=1,这里取α=0.75,β=0.25。当Fitness全局最大值时,云平台同时具有较短任务执行时间和较小负载均衡度。
3 云仿真任务调度及迁移流程
调度及迁移步骤如下:
Step1:周期采集每个虚拟机上CPU、内存及网络带宽的占用率。
Step2:利用CBPSO算法计算当前各虚拟机的负载度和适应度,云平台虚拟机集群总的负载均衡度、最大适应度、最小适应度。
Step3:当负载均衡度超出设定阀值时,将适应度最小虚拟机上的子任务迁移到适应度最大的虚拟机上。
Step4:当仿真子任务迁移完成后,重新计算当前云平台虚拟机集群总的负载均衡度。若负载均衡度未超出设定阀值,则证明调度成功,在下一个信息采集周期重复上述过程;若负载均衡度超出阀值,返回Step3。
4 云仿真任务调度算法设计
求解子任务与虚拟机最优的组合方式即为:在离散二进制粒子群中,利用CBPSO算法搜索使适应度函数Fitness达到最大值的全局最优位置向量Pg:

其中,xr,j=1,rj代表与任务j匹配的虚拟机,n为仿真子任务数量。
4.1 位置及速度的更新
在BPSO中,粒子位置更新就是位置向量xij在“0”和“1”之间的转换,速度vij的大小代表xij下一步转变为“1”的概率[5]。为了使vij代表粒子的位置转变概率,引入限制函数sig,使速度vij位于(0,1)之间[5],其公式为式(6)。

其中,vij∈(0,1)。
粒子的位置与速度更新公式为:

Step 3:根据式(5)计算每个粒子的个体适应度fi,进而确定种群个体的历史极值位置Pi和全局最优位置Pg。
Step 4:按式(6)~式(8)迭代更新粒子位置、速度。计算新一代粒子的适应度,更新Pi和Pg。
Step 5:依据式(11)求出当前种群的适应度方差σ2,若σ2小于阀值(设阀值为0.1),即认定当前粒子群收敛到全局最优解或陷入局部极小解,转Step 6。
其中:k为迭代次数,pij为粒子个体局部最优位置,pgj为种群全局最优位置,c1和c2为学习因子,rand( )为[0,1]之间的随机数。
通过式(6)、式(7)可以看出:在迭代初期,粒子的速度较大,粒子位置编码以大概率向“1”转变,BPSO算法在种群内快速搜索;在迭代后期,当多数粒子位置编码转变为“1”后,粒子位置的转变概率不断减小;当算法搜索到最优位置向量pg时,转变概率为“0”,算法搜索结束。
4.2 混沌搜索策略
BPSO和其他智能算法一样,同样具有易于陷入局部极值的缺点。为避免BPSO算法过早收敛于局部最优值,出现早熟现象,将BPSO算法与Logistic混沌算法结合,利用Logistic混沌映射初始化种群中粒子的位置和速度,使粒子随机、均匀的散布到解空间;一旦BPSO算法陷入局部极小值,利用Logistic混沌映射在局部极小值附近进行局部扰动,使算法快速逃离局部极值。Logisti映射公式如下[6]:

其中:μ为混沌映射因子,μ=4。
加入Logistic混沌搜索的BPSO算法流程如下:
Step 1:初始化粒子群参数,种群规模Q,维度n,学习算子c1、c2,最大迭代次数Zmax等。
Step 2:随机初始化种群,设定n维初始化位置序列X1=[x12,x11,…,x1n],x1i∈[0,1],n维初始化速度序列V1=[v12,v11,…,v1n],v1i∈[0,1];利用Logisti映射公式(9)对序列X1、V1迭代k-1次得到位置序列Xk=[xk2,xk1,…,xkn],xki∈[0,1]速度序列Vk=[vk2,vk1,…,vkn],vki∈[0,1]。
由于BPSO中,粒子位置只能为0或1,通过式(10)将Xk转换成二进制序列

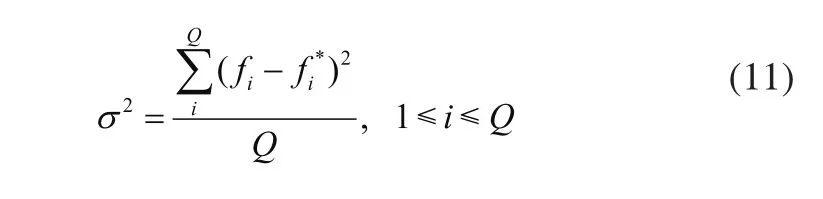
其中:fi为粒子适应度值,为当前粒子群适应度的平均值,Q为种群规模 。
Step 6:如果算法迭代次数达到Zmax,寻优结束,返回全局最优解位置Pg及适应度值Fitness,否则跳至Step 7。
Step 7:选取20%Q个适应度值最高的粒子,按照Step 2的方法执行局部混沌扰动更新Zmax,重新执行Step 1~6。
5 仿真实验
本文在云仿真软件CloudSim上进行仿真实验,在相同的实验环境下对CBPSO、BPSO和CloudSim自带的贪心算法进行仿真对比。分析不同算法对任务总执行时间、平均任务响应时间、负载均衡度的影响。实验中,设定最大迭代次数Zmax=200,总群规模Q=100,学习因子c1=c2=2,各虚拟机和仿真子任务的配置信息如表1~表2所示。

表1 虚拟机配置参数

表2 仿真子任务配置参数
5.1 CBPSO与BPSO收敛速度对比
图1为CBPSO和BPSO的适应度收敛曲线。可见,CBPSO收敛速度更快,全局寻优能力更强。BPSO迭代116次后陷入局部极值。
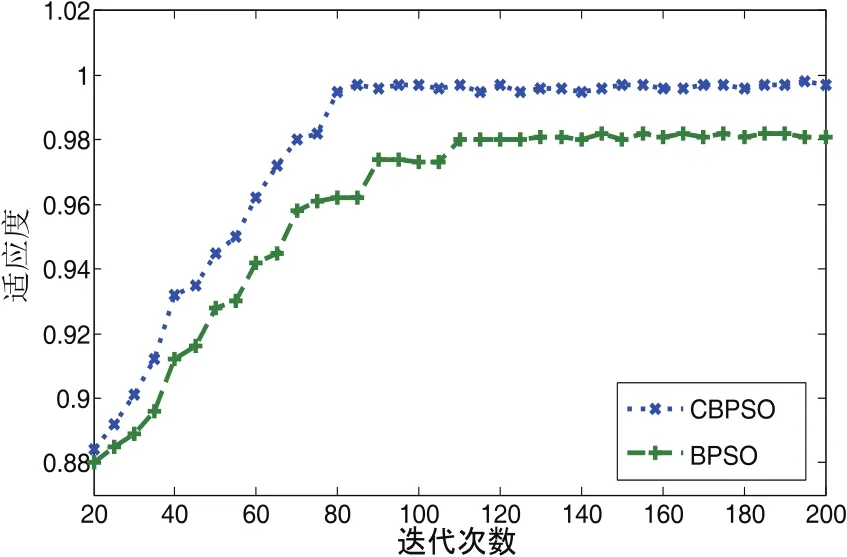
图1 适应度收敛曲线
5.2 任务总执行时间、平均任务响应时间
任务总执行时间代表所有子任务执行完成所使用的时间。平均任务响应时间表示从所有子任务到达虚拟机至子任务在虚拟机上执行完成并提交给用户所用的平均时间。三种算法的任务执行时间对比如图2所示,平均任务响应时间对比如图3所示。

图2 任务总执行时间

图3 平均任务响应时间
图2、图3表明,CBPSO的任务总执行时间和平均任务响应时间比其他两种算法都短,系统的运行效率更高。
5.3 负载度均衡度
三种算法的负载均衡度对比如图4所示。

图4 负载均衡度
从图4可以看出,贪婪算法的负载均衡度最大,且波动性比较大。BPSO算法下,云仿真平台的平均负载均衡度为0.278。CBPSO算法下,云仿真平台的平均负载均衡度为0.212,说明此算法下,虚拟机集群负载均衡性最好。
6 结论
仿真实验证明,基于CBPSO算法的云仿真任务调度策略在任务总执行时间、平均任务响应时间、负载均衡度方面的性能指标都高于BPSO和贪心算法。同时也证明混沌算法可弥补BPSO易于陷入局部极值的不足。
