多重指示克里格法在坦桑尼亚某金矿床储量估算中的应用

黄 松，谢玉玲

(1.北京科技大学土木与资源工程学院，北京 100083；2.澳大利亚隆格矿业咨询有限公司，北京 100026)

法国统计学家MATHERON在《Traité de géostatistique appliquée》一文最早提出地质统计学的概念[1]。MATHERON教授根据自己的研究成果提出区域化变量的概念，最终创立了地质统计学。地质统计学基于区域化变量，采用变异函数作为研究的主要工具。需要在同时考虑具有规律空间分布和局部数据相关的数据分布的不同特征的情况下，对这些数据进行最优无偏内插估计，或需要在模拟这些数据的离散程度以及不同区域不同分布特征情况下，将地质统计学的基础理论与研究方法引入到具体的研究进程中。根据地质统计学的基本理论，与地质体相关的各种地质特征(包括品位、岩性、蚀变、水文、物化探等信息)都可以借助区域化变量的空间分布特征来表征。在研究区域化变量的空间分布特征和相关关系的过程中，选取变异函数作为主要研究工具来对这些特征进行分析[2-3]。地质统计学分析估值方法主要包括简单克里格(SK)、普通克里格(OK)、泛克里格(UK)、协同克里格(CoK)、指示克里格(IK)等估值方法，作为非参数估值法代表的指示克里格法，主要适用于空间变异性较大的物性参数空间估值，估计结果能绘制出比较光滑的图形，在目前的数值估算领域得到了广泛的应用[4-7]。

矿山三维地质建模是数字化矿山的关键技术之一，是研究地质体三维模拟流程与通过软件进行可视化的核心与基础。与传统二维地质建模相比，三维地质建模将空间信息管理、基础地质解译、地质统计学分析、矿化实体分析以及三维图形可视化等工具结合，并用于地质分析，能更加形象、准确再现地质单元的空间展布及相互关系，为矿山的合理开采以及深部找矿提供科学依据。

自20世纪90年代以来，地质统计学基础理论持续发展并日渐成熟，同时伴随着计算机技术的不断革新，基于地质统计学原理的各种三维矿业统计分析、估值软件不断开发出来并能在理论日益发展的基础上不断得到更新，如IDRISI、GEO-EAS、GS+、Surfer、GeoDA、Surpac、Datamine、Vulcan等国外软件和CGES、3Dmine、DIMINE等国产软件，都发展成为市场上使用接受度相对较高的地质学统计与估值软件。

本研究借助Surpac矿业软件，对坦桑尼亚某金矿进行三维模型的构建，运用地质统计学的多重指示克里格法，对其品位分布进行统计分析进而确定多个估值阈值，优化并确定块体模型估值参数以及克里格变异函数参数，并最终对储量进行估算，为矿山进一步的勘探和生产规划提供技术支撑[8-10]。

1 研究矿区地质特征

坦桑尼亚位于非洲板块的东部，区域内主要多多马克拉通地块是东非克拉通南段地块的一部分。本文研究的矿床位于穆索马-马拉绿岩带的北马拉地区，穆索马-马拉绿岩带是坦桑尼亚克拉通的维多利亚湖金矿成矿区域的一部分。太古代的绿岩带由东-西走向的逆冲断层带区域组成，沿着该逆冲断层带向北地质年代逐渐由较新地层向较老地层更替。绿岩带向东延伸100 km，从维多利亚湖东部边缘的穆索马镇一直延伸到与肯尼亚的交界位置(图1)。

穆索马-马拉绿岩带中，岩石的类型种类比较复杂。在南部的穆索马地区，金矿赋存的最老岩层是尼安萨超群，由基性以及长英质熔岩、凝灰岩以及多层倾伏向趋近于0°的水平发育条带状铁建造组成，各个铁建造的条带构造中一般含少量黄铁矿；在北部马拉地区，主要由基性以及长英质火山岩构成，上覆片麻岩和片岩，这几个主要岩层共同构成尼安萨超群。尼安萨超群上部主要覆盖的一层卡维隆多超群粗粒碎屑沉积岩，向北延伸可到达肯尼亚境内，不是矿化主要赋存岩层，在其中极少观察到矿化。研究区内所有岩层都经历了绿片岩相变质作用，之后形成局部褶皱，大部分褶皱轴向北东。

穆索马-马拉成矿带中大部分金矿化赋存在石英矿脉中，石英矿脉一般含有黄铁矿、金及少量其他金属硫化物。围岩发生碳酸盐化。

图1 坦桑尼亚某金矿矿床地质图Fig.1 Gold deposit geology map in Tanzania

穆索马-马拉绿岩带中多数矿床的控矿构造为各种后生断层，代表性的两组断层方向分别为60°方向和130°方向，对矿床分布起重要约束作用。

在局部地区，未变形的元古代沉积岩，覆盖在太古代序列之上。该地区经历了几个期次的变形，最后发育形成东非大裂谷。与大裂谷相关的张性构造伴随响岩熔岩流的溢出，它覆盖了北马拉大部分地区。

本文研究矿床赋存于剪切带内的太古代安山质火山岩中，期间夹有薄层沉积岩所有重要的金矿化都被限制在这套地层的围岩中，如图1所示。矿化岩体由一系列似板状的、陡倾斜的蚀变岩组成，赋存于单一的、由安山质火山岩组成的火山岩岩组中。

2 三维建模于原始数据分析

2.1 数据库建立

数据库的建立流程主要包括：收集矿区内所有的勘探资料，包括槽探、钻探、坑探等地质资料，通过地质编录对岩性、地层、断层、蚀变、含水层等分布情况进行记录，然后将数据导入Surpac建立用于后续的数据分析和模型估值相兼容的原始数据库。地质数据库的建立是利用三维地质信息在三维建模估值软件的协助下完成矿区范围内地质信息的三维化，并结合地质统计学进行储量估算的首要基础，直接影响建立的三维模型的合理性与估值结果的合理性。本次工作共收集矿区内8 090个地表和地下钻孔和探槽的相关信息，并建立地质数据库基本表，其中，钻孔孔口表主要包括钻孔的开孔坐标、钻孔深度、钻探类型、时间以及孔迹；钻孔测斜表主要包括钻孔的方位角及倾角;钻孔化验表主要包括钻孔的采样品位(主要包括金、银等品位信息)；钻孔岩性表主要包括岩性、地层、断层、蚀变、含水层等相关地质信息。

2.2 三维模型建立

通过解译地质资料，自动和手动利用三角网联接技术，可以创建各种复杂形态的矿体实体模型。从建模所使用的数据源来看，主要包括野外收集数据、剖面提取数据、分散观测点数据、原始钻孔数据、物化探等多源数据。本次矿体建模采用3D模型，主要基于剖面图和钻孔数据资料进行地质解译，创建总共20个矿体的三维实体模型(图2，矿体1200为样品主要分布区域，作为本文主要研究对象)。

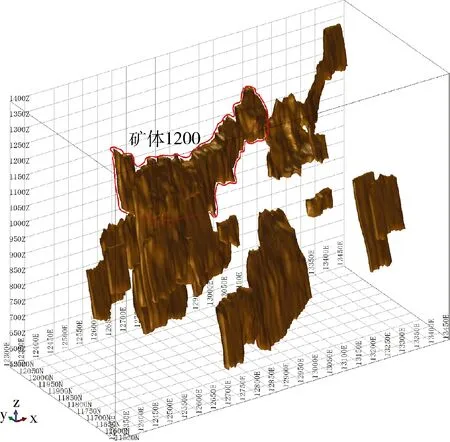
图2 矿体三维视图Fig.2 3D view map of ore bodies

2.3 原始数据分析

在进行样品的基本统计分析和变异函数分析之前，样品组合可以修正不同样长样品权重，是数据分析必不可少的环节。可以选择多种方法进行样品的组合，如按钻孔钻进方向进行组合、按台阶进行组合、按地质分带进行组合、按实体相对内外部位置进行组合等。在样品组合过程中，为了避免发生局部区域样品分割过小产生额外地质信息或者整体组合长度过大导致品位过度平滑的情况，需要考虑多种因素以最终确定样品组合长度，原始样本长度、勘探网度、最小开采单位、块体模型尺寸等因素都会影响组合长度的选择。本次选用“按钻进方向与地质分带组合方法”进行样品组合。本研究矿体矿化线框(“区域”)用于为化验数据库编码，以允许识别各种地质界限与可能存在的交集。随后完成样品长度的检查，以确定最优组合长度。矿化线框内部普遍的样品长度为1 m，样品长度均值也接近1 m，所以1 m作为首选组合长度。经过样品组合后，金金属元素数据采用Supervior统计软件进行统计分析，分析结果如图3所示。原始品位分布柱状图中(图3(a))，样品不服从标准正态分布，在200 g/t到2 300 g/t品位空间内有少量高品位样品分布；原始品位对数分布柱状图中(图3(b))，对数柱状体基本符合正态分布，可以作为选用对数克里格或者指示克里格方法的依据；金品位概率分布图显示品位0.1～1 g/t之间存在拐点位置，与目前采用的0.5 g/t的地质边界品位相一致。

3 估值方法选择与原理分析

在各种克里格估值方法中，普通克里格应用最为普遍，但是局限性在于需要原始数据或者指数转换后数据满足正态分布，同时由于部分特高品位的存在会影响变异函数曲线的拟合度，需要消除特高品位在矿床局部的影响，特高品位处理是必要的。作为另外一个经典的非参数地质统计学方法，指示克里格无需假设数值来自某种特定的分布母体，也无需对原始数据进行转换，可以在不必要去掉具有代表性而实际存在的特高值数据的前提下进行各种数据分析与估值计算。可以通过不同阈值的设置，控制估值的过程精度，揭示一定风险条件下未知量Z(x)的估值量及空间分布情况。同时，根据原始样品的统计学数据，样品数据上限值大于数据均值+9倍标准差，同样说明高品位样品对于该矿床的品位估算的影响不能直接忽略，指示克里格方法相较于其他估值方法更有优势[11]。

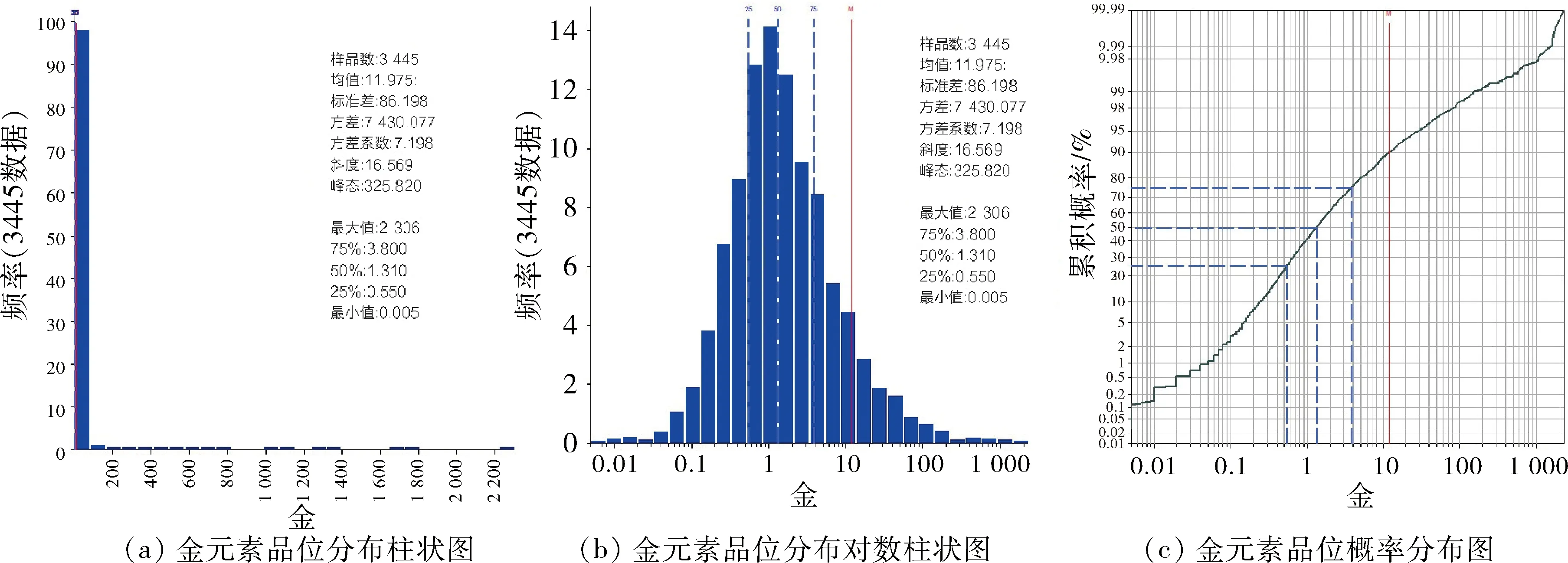
图3 样品柱状图和概率分布图Fig.3 Samples histograms and probability map

指示克里格估值方法的一般原理是根据阈值对原始数据进行二进制编码，对于任何数值Z(x)有如式(1)的关系式。

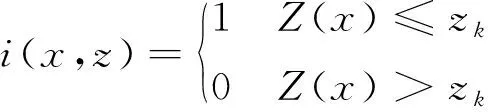
(1)

由式(1)可知，指示变换是一种将原始数据重新进行非线性变化的一种方法，所有大于选定阈值的数值会同意转换为1，无论数值是否位于异常值界限以上或是以下。在给定zk的条件下，i(x+h;z)和i(x;z)代表向量h分隔的两个区域化变量，可以定义指示变异函数及实验指示变异函数，见式(2)和式(3)。

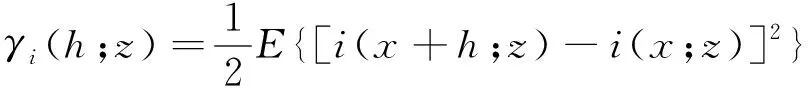
(2)

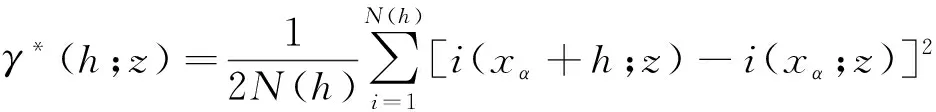
(3)

式(3)中N(h)是步长为h数据的对的数目，用于实验指示变异函数计算的不是原数据，而是原数据经过转换后的指示函数，所以指示变异函数对于一些极值数据有极强的适应能力，能保证整体估值结果的稳健。根据各个品位阈值对应的指示值求解指示克里格方程组将获得各个位置点或者区域的条件累积分布函数，计算结果代表该位置的不确定性概率模型，具体见式(4)。

α=1,2,…N}

(4)

完成各个阈值区间的概率分布数值后，结合各个区间的中位均值，求解函数积分即可以根据以下公式求得指示克里格估值法对于指定区域化变量在某个特定点或者区块的估值结果，见式(5)。

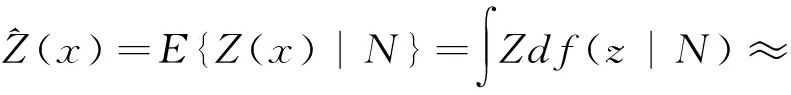
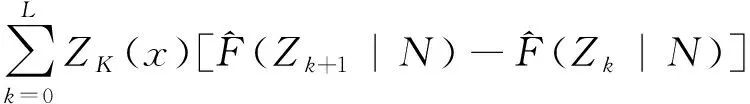
(5)

结合以上的原理解释以及估值软件的一般参数设置过程。指示克里格估值方法的流程图见图4。

4 块体模型基础参数优化

在创建块体模型的时候，需要选择合理的块体尺寸，而在针对每个指示克里格品位区间进行估值过程中，需要选择合适的最大样品数以及椭球体最大搜索半径。本文通过建立三个处于不同样品分布密度位置的类似单块体模型，同时选取条件偏差斜率和克里格效率值两个特征参数，对块体尺寸、估值最大样品数和最大搜索半径等参数进行分析，以选取合理的取值范围[11-12]。三个单块体模型分别来自高密度块体(优秀)、中密度块体(良好)和低密度块体(差)。经过试验单体模型的建立以及估值软件的估值实践，关于块体尺寸、最大样品数和搜索半径的曲线对比图如图5所示。

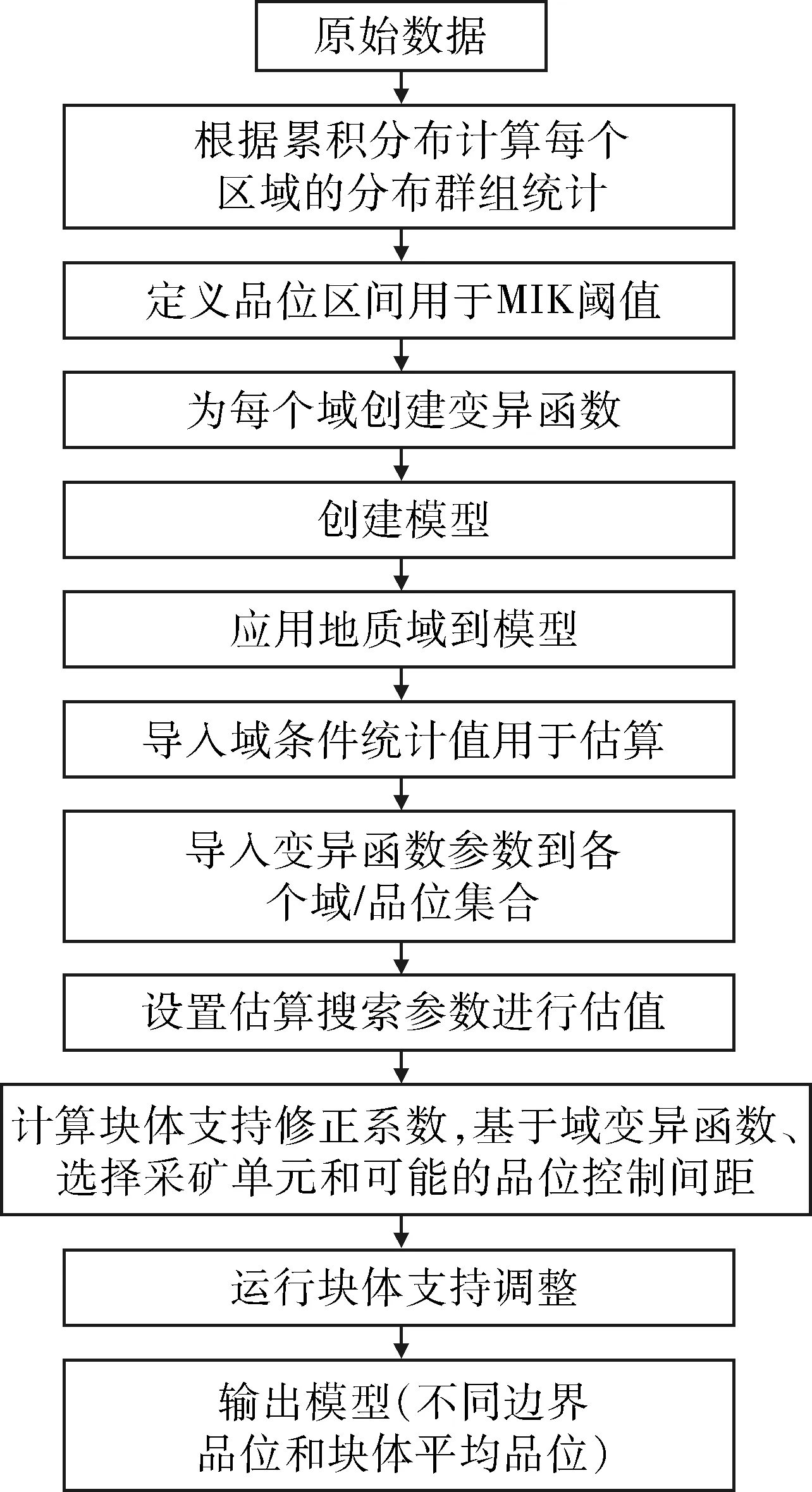
图4 克里格估值方法流程图Fig.4 Flowchart of Kriging estimation methods

图5(a)显示，随着块体尺寸的逐渐增长，除了斜率(良好)与斜率(差)一直处于较低水平，其他四条曲线都有类似的平缓到缓慢减少到急速下降的趋势。可以看出，经过回次4到5附近的拐点之后，斜率与克里格效率值逐渐降低，估值结果的精确度也大幅度降低。同时，回次4之前过小的块体尺寸会对软件运算速度有更严苛的要求且耗时较长，综合考虑选取选取回次5对应的10 m×10 m×5 m作为主块体尺寸。图5(b)显示，最大样品数直接与邻近区域样品分布密度有关，在样品数量达到40个或者更多之后，曲线趋于平缓，所以大于等于40的样品数可以作为估值最大样品数。图5(c)显示，样品分布情况较差的曲线相比于样品分布情况好的曲线，在随着搜索半径逐渐扩大的过程中，趋于平缓的过程会更长一些，考虑到选取参数需要适应全局范围内的所有块体，所以选取大于等于90 m作为最小搜索半径。

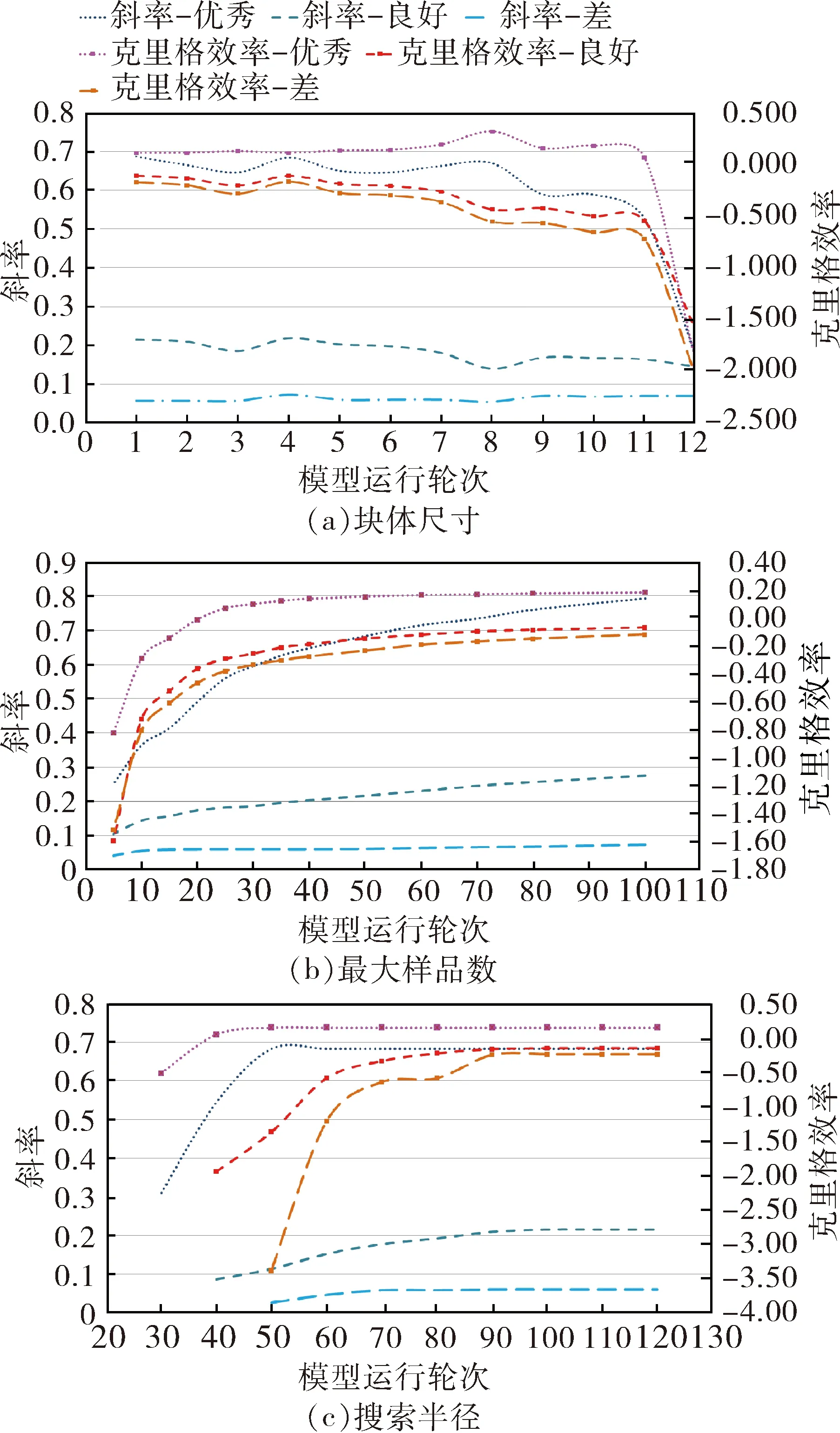
图5 克里格参数优化对比曲线图Fig.5 Kriging parameters optimization comparison chart

块体模型基础参数的研究对各个参数取值区间的确认至关重要，能更好地保证块体模型与基础地质数据的兼容性和最终估值结果的准确性。

5 指示克里格参数设置

运用分位数法选择指示边界品位后，结合金矿石的边界品位和工业品位，将整个样品数据结合根据品位百分比划分为13个阈值区间，从0%到90%样品数量区间，采用10%为各个区间覆盖范围长度变化量；在90%到100%样品区间，由于数量可观的特高品位样品的存在，采用相对较小的范围长度变化量，以实现在不同阈值区间得到大部分特高品位值的不同非参数转换值，进而对特高品位值的分布实现更为精确的定位，赋予更为合理的权重。针对各个阈值区间，分别建立对应的变异函数模型，完成对变异函数结构参数的提取。图6为分别对应于40%样品阈值区间和99%样品阈值区间的三轴变异函数模型。

完成总共13个阈值区间的变异函数分析与参数提取后，即可得到对应每个阈值区间的参数汇总表，见表1。

6 指示克里格估值结果合理性验证

合理性验证是用来检验根据变异函数曲线拟合所得参数进行品位估算结果的合理性与正确性，同时也能直接显示组合样品位与估值品位的相关程度。其原理是比较在各个矿体分段区间内已估值的品位与真实值之间的偏差，并对其区别和变化进行统计分析，结果见图7。

图6 变异函数拟合曲线图(40%与99%品位区间)Fig.6 Variogram fitting curves

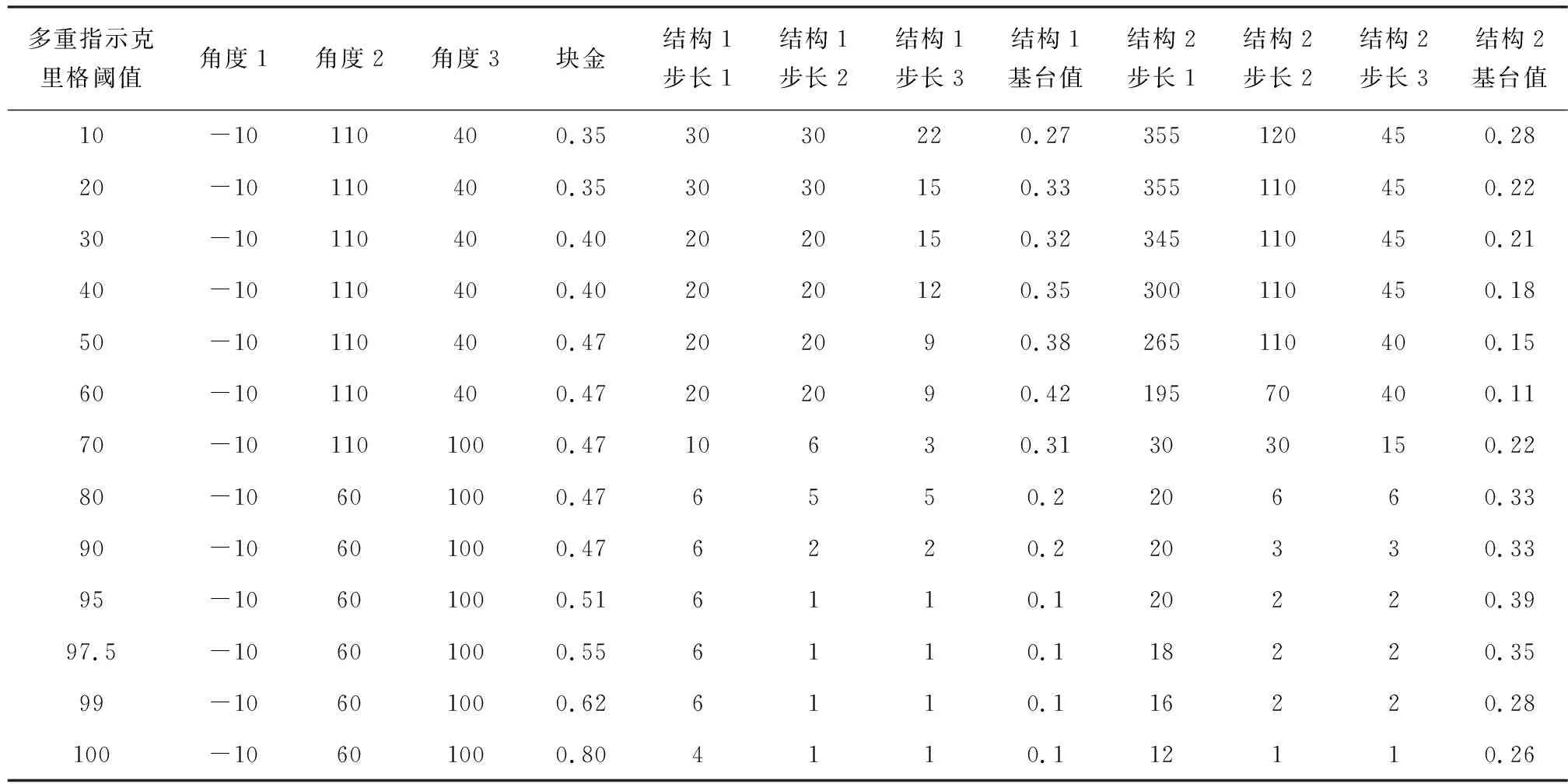
多重指示克里格阈值角度1角度2角度3块金结构1步长1结构1步长2结构1步长3结构1基台值结构2步长1结构2步长2结构2步长3结构2基台值10-10110400.353030220.27355120450.2820-10110400.353030150.33355110450.2230-10110400.402020150.32345110450.2140-10110400.402020120.35300110450.1850-10110400.47202090.38265110400.1560-10110400.47202090.4219570400.1170-101101000.4710630.313030150.2280-10601000.476550.220660.3390-10601000.476220.220330.3395-10601000.516110.120220.3997.5-10601000.556110.118220.3599-10601000.626110.116220.28100-10601000.804110.112110.26

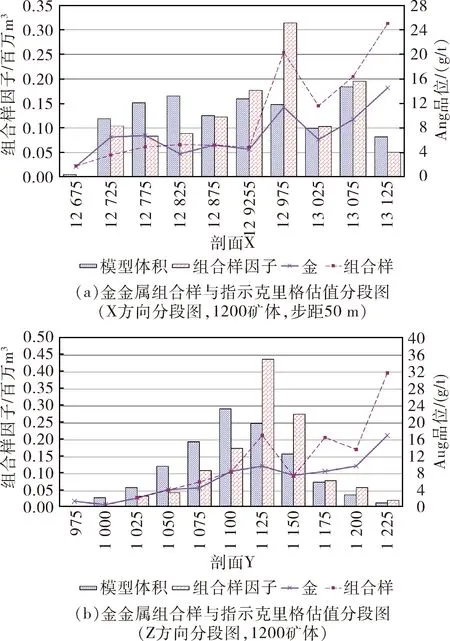
图7 储量估值结果分段图验证结果Fig.7 Resource estimation results swats plots

通过块体模型分段图的分析，从图7中可以看出，估值结果曲线以及原始数据曲线在各个矿体分段中拟合程度较高，确认了估值结果与原始结果的高度相关性。同时，部分高品位区段的品位经过克里格估值方法处理之后，平滑效应导致品位分布更为合理。各个分段相关块段结合了周围合理数量的原始样品进行估值，并通过指示克里格自身的特点保留了高品位段对整个矿床品位分布的贡献，得到了合理的估值结果。

7 储量估算结果

本研究建立了主要矿化体矿区范围内的块体模

型，储量估算选择的块体模型的块体大小为10 m×10 m×5 m，次级块体大小为可变块体尺寸，在矿体边界区域会根据矿体围岩接触情况进行调整。运用已提取处理的组合样品，对块体模型中块体进行品位估值，选择指示克里格法进行估值，将计算好的每个阈值区间椭球模型相对应的块金值、基台值、变程值等相关参数导入，结合所有原始样品的指示转换值计算出对应与每个阈值区间的条件概率密度，然后与相应区间原始样品品位均值的乘积求和即可得到每个待估块的估算值。完成品位估算后，即可得到矿体的矿量、金属量等数据，全局品位分布图可见图8，通过总矿量和品位计算总金金属量过程可参考式(6)。

Qm=Ci×Vi×ρ

(6)

式中：Qm为金属量；Vi为块体体积；Ci为块体平均品位；ρ为矿石体重。运用Surpac三维地质建模估值软件进行储量计算，计算出金矿石总矿量为1 400万t，总金金属量为275万t。同时，本次研究将2018年指示克里格估值结果与2016年普通克里格估值结果做了直接对比，详细储量报告表见表2。

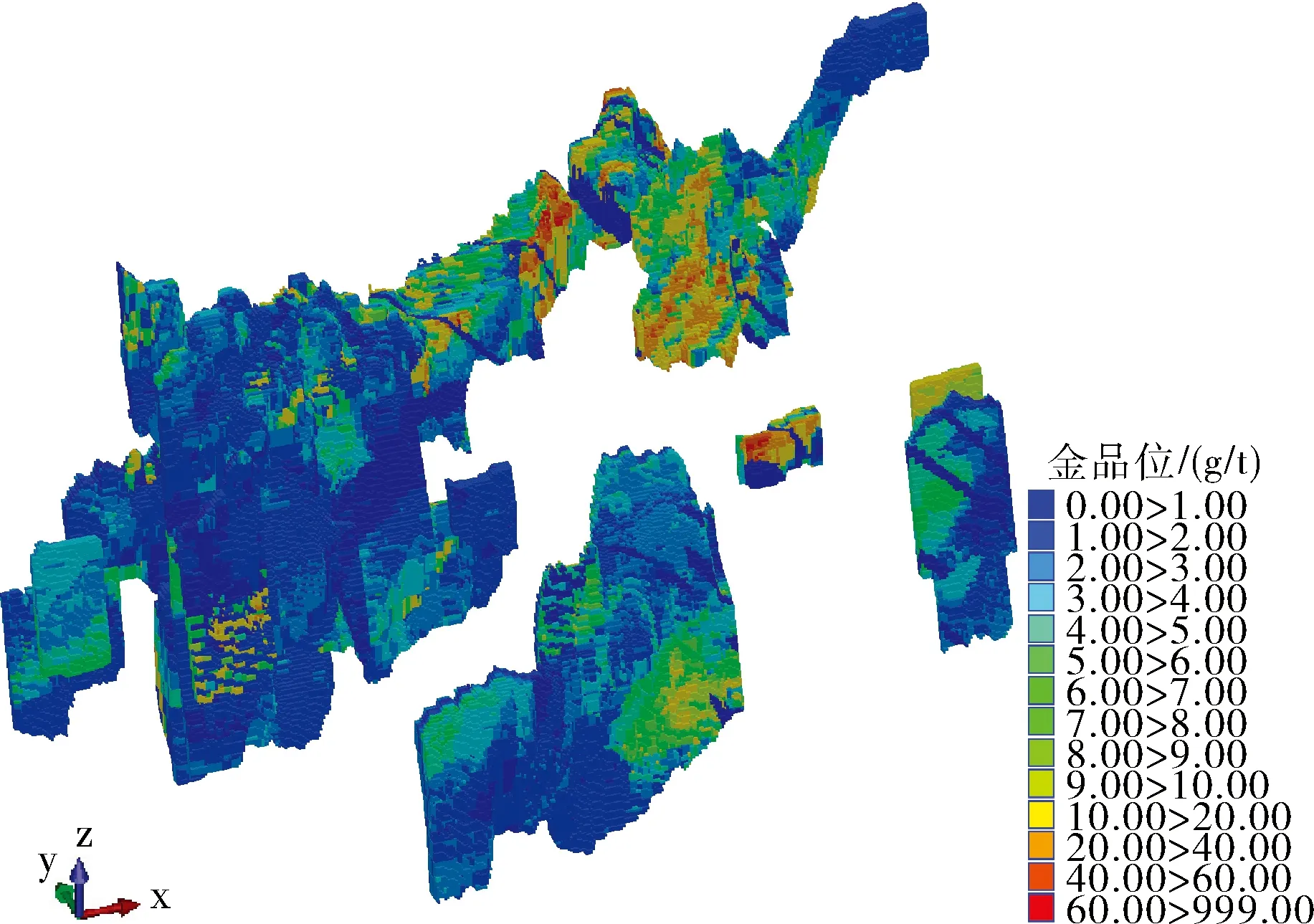
图8 矿体模型(品位分布着色)Fig.8 Block model of ore bodies (Colored by grades)

表2 储量估算结果对比表(未采用品位约束)Table 2 Resource estimation results comparison table (No cut-off grade applied)

从表2中可以看出，2018年估值结果相较于2016年估值结果整体矿量和部分矿化区域的平均品位有明显的提升。主要原因为：①2016～2017年最新的勘探钻孔定义了少量矿化延伸区域；②比重样品取样优化，大体重样品的比例有所提高；③采用指示克里格法进行估值，保留了整体矿化样品中一定比例的特高品位样品对整体矿体估值的贡献，进而影响并提高了整体的矿化区域矿量和估值品位。

8 结 论

1) 应用多重指示克立格法求出在不同边界品位下的指示值，进而可以查看任一待估块段中每个品位级别所占的比例。指示克立格法不要求区域化变量服从某种分布，不需要进行特异值处理，因此认为指示克立格法比其他统计学方法更具有优势，更适用于特高品位广泛分布的金矿床的储量估算。

2) 针对块体模型估值参数设置中的部分关键参数，运用KNA类比分析方法比较了不同参数选取下估值结果的克里格效率值并经过分析确定了最优参数；同时，针对克里格估值过程阈值选定，结合原始数据基本分析结果，对十分位分段原则进行了局部调整，放大了高品位区间数据对整体品位估算的影响权重。

3) 本文最终计算出该矿床总矿石量为1 400万t，总金金属量为275万t，相较于历史估值结果，储量和平均品位都得到了一定的提高。与传统的距离反比法、普通克里格法相比，指示克里格保留了特高品位在局部对矿山整体品位分布的贡献值，与真实品位分布情况拟合度更高。将块体模型分段图运用到估值模型验证工作中，确认了估值方法与结果的合理性，可以为矿山未来的接续勘探和开采生产提供进一步的理论指导。