Doubly Excited 1,3Fe States of Two-Electron Atoms under Weakly Coupled Plasma Environment∗

S.Dutta, J.K.Saha, S.Bhattacharyya, and T.K.Mukherjee

1Belgharia Texmaco Estate School,Belgharia,Kolkata 700056,India

2Department of Physics,Narula Institute of Technology,Agarpara,Kolkata 700109,India

3Department of Physics,Aliah University,IIA/27,Newtown,Kolkata 700160,India

4Department of Physics,Acharya Prafulla Chandra College,New Barrackpore,Kolkata 700131,India

Abstract Precise energy eigenvalues of metastable bound doubly excited 1,3Fe states originating from 2pnf (n=4–6) configuration of helium-like ions (Z=2–4) under weakly coupled plasma (WCP) environment have been estimated within the framework of Ritz variational method.The wavefunction is expanded in explicitly correlated Hylleraas type basis set.The screened Coulomb potential is consideredas mimic the WCP environment.The atomic systems tend towards gradual instability and the number of excited metastable bound states reduces with increasing plasma strength.The wavelengths corresponding to 2pnf (1,3Fe) →2pn′d (1,3Do) (n=4–6; n′=3–6) transitions occurring between doubly excited states of plasma embedded two-electron ions are also reported.

Key words: two-electron atom,doubly excited states,variational method,weakly coupled plasma,Hylleraas co-ordinate

1 Introduction

Doubly excited states (DESs) of two-electron atom is a topic of active interest in recent times,both from theoretical and experimental aspects.[1−9]The abundance of such DESs is noted in various astrophysical observations as well as in high temperature laboratory plasma.[10−19]The DESs of two-electron atom having unnatural parity(π=(−1)L+1,Lis the total angular momentum quantum number) and lying below the second ionization threshold,are metastable bound.These states favorably can decay to a lower state via radiative process rather than decaying through non-radiative autoionization channel.Examples of such DESs of unnatural parity are1,3Pe,1,3Do,1,3Festates arising out of dominantpp,pd,pfconfigurations respectively.

Atomic systems under external environments have been studied by various researchers during the past several decades,as they provide useful information about the environment.A large number of investigations[20−30]are there in the literature on the modified properties of plasma embedded atomic systems.Extensive review articles[31−32]are available on this topic.Plasma coupling strength (Γ) is defined as the ratio between average inter-particle electrostatic energy to the average thermal kinetic energy.The high temperature and low density classical plasma are categorized as weakly coupled(Γ<1).According to the Debye-Hückel theory[33]a short range Yukawa-type or screened Coulomb model potential is considered to mimic the modified inter-particle interaction under WCP environment.Due to its simplicity and effectiveness,such screened Coulomb potential has been used widely by researchers for the investigation of spectral and structural properties of atomic systems under WCP environment.In this model,plasma electron density(ne)and temperature(T)are combinedly expressed through the plasma screening length(D).[33]As the screened Coulomb potential is more positive in nature than the “pure” Coulomb potential,in general,with the decrease of plasma screening length(D),the energy levels are pushed up and the gap between two successive energy level decreases.[20]This causes the transition energy to decrease and a red shift[21]may be observed.However,it is remarkable that for some specific transitions between two doubly excited energy levels,the wavelengths get blue shifted or show a pattern with both red and blue shiftw.r.t.the plasma screening length (D).[21]

In the present work,we have estimated the non-relativistic energy eigenvalues of doubly excited metastable bound 2pnf(n=4–6) (1,3Fe) states of two-electron ions(Z=2–4)as well as the 2sand 2pstates of the respective one-electron ions under WCP environment.According to the Debye-Hückel theory,[33]in a two-electron Hamiltonian,the effect of plasma screening should be reflected in both the one-particle electron-nucleus attraction terms and the electron-electron repulsion term of the total potential.Although the effect of screening on the electronnucleus attraction term predominates overthe electronelectron repulsion term in determining the properties of plasma embedded two electron atom,we have considered the effect of screening on both attractive electron-nucleus part and repulsive electron-electron part in the potential.Computationally,it is difficult to include the effect of screening in repulsive electron-electron part even for a partially correlated CI type basis constructed with Slatertype orbitals as the analytic solution of the corresponding basis integrals becomes extremely cumbersome.[34−35]However,we have been able to develop the methodology to estimate the basis integral for the trial wavefunction is expanded in multi-exponent Hylleraas type basis set in a way that the effect of screening in repulsive electronelectron part has been considered fully without any perturbative approximation.Ritz variational method is used to determine the energy eigenroots.The wavelengths for the dipole allowed transitions between doubly excited metastable bound states 2pnf[n=4–6](1,3Fe)and 2pn′d(n′=3–6) (1,3Do) are determined for different values of plasma screening length(D).The non-relativistic energyeigenvalues of 2pnd(n=3–6) (1,3Do) states are taken from an earlier work of Sahaet al.[21]The details of the methodology are given in Sec.2 followed by the discussion on the results in Sec.3 and finally concluded in Sec.4.

2 Method

The non-relativistic Hamiltonian (in a.u.) of a twoelectron atom immersed in WCP environment may be written as

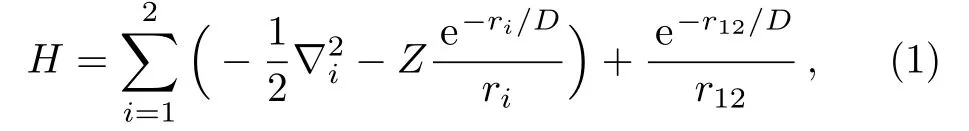
where,in case of screening by both ions and electrons,the Debye screening length (D) reads as[33]

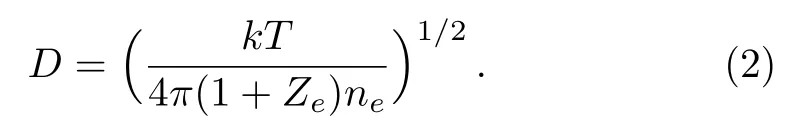
For a fully ionized plasma comprising of a single nuclear species,the effective nuclear charge isZe=Zwhereas in case of screening by electrons only,Ze=0.After seperation of the centre of mass coordinates,the wave function of1,3Festates due to dominantpfconfiguration of a twoelectron atom can be written in terms of six co-ordinates(r1,r2,θ12;θ,φ,ψ) as,[36−37]

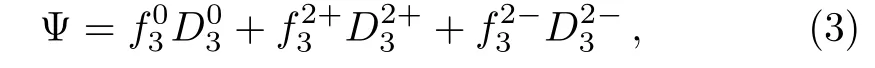
where,are the rotational harmonics and functions of three Eulerian angles (θ,φ,ψ) that define the orientation of the triangle formed by the two electrons and the nucleus in space;κis the angular momentum quantum number about the body fixed axis of rotation.[36]The radial parts of the wavefunction are given by=−F1sinθ12,=where,with the conditionandθ12is the angle betweenandThe upper sign corresponds to the singlet state and the lower sign to the triplet state.The trial radial wave function corresponding topfconfigurations is expanded in Hylleraas basis set as

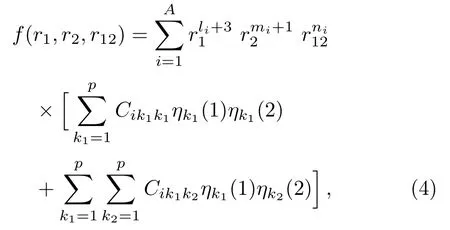
with the features: (a) The powers ofr1,r2andr12satisfies (li,mi,ni)≥(0,0,0); (b)Ais the total number of (li,mi,ni) set considered in the calculation; (c)ηi(j)=e−ρirjare the Slater-type orbitals whereρ’s are the non-linear parameters; (d)pdenotes the total number of non-linear parameters; (e) In the double sum of Eq.(4),k1< k2; (f)Cik1k2are the linear variational parameters.The effect of the radial correlation is incorporated through differentρ’s in the wave function whereas,the angular correlation effect is taken care of through different powers ofr12.The number of terms in the basis set expansions for the trial radial wave functionfis thereforeN=[p(p+1)/2]×A.In the present case,we have considered a nine-exponent (p=9) basis set where the non-linear parameters are taken in a geometrical sequence followingρi=ρi−1γ,γis the geometrical ratio.After choosing the proper trial radial wave function,the energy eigenvalues are obtained by solving the generalized eigenvalue equation.[38]The details regarding the analytic evaluation of the correlated basis integrals are discussed in Duttaet al.[38]

The variational equation for thenl-state of the respective one-electron atoms under WCP environment can be written as

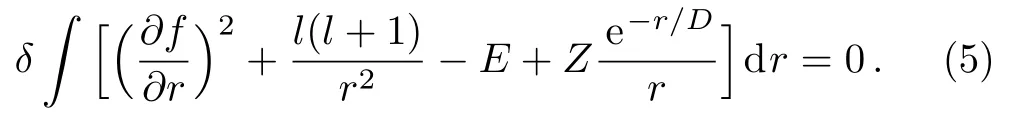
The radial functionf(r) is expanded in terms of a pure exponential basis set as

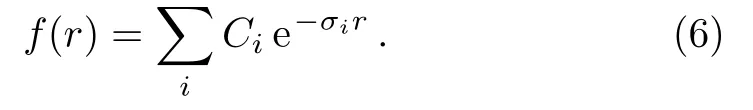
We have used 101 number of terms in the basis set and the exponents are taken in a geometrical sequenceσi=σi−1β,βis the geometrical ratio.The energy eigenvaluesE’s and linear variational coefficientsCi’s are determined by matrix diagonalization procedure.All calculations are carried out in quadruple precision.Such procedure is repeated for different plasma screening length (D) considered in the present case.

3 Results and Discussion

Table 1 shows the convergence behavior of the energy eigenvalues of 2pnf(n=4–6) (1,3Fe) states of He with respect to the total number of termsN=540 andN=675 in the 9-exponent basis set for three different Debye screening lengthsD=100,50,and 20(in a.u.).It can be seen from Table 1 that,all the energy eigenvalues converge at least up to sixth decimal place forD=100 a.u.andD=50 a.u.whereas,energies of 2p5fand 2p6fconverge up to fourth and third decimal places respectively forD=20 a.u.The energy values of 2pnf(n=4–6)(1,3Fe) states of two-electron ions (Z=2–4) in the presence of WCP environment are given in Tables 2–4 respectively.Only the values obtained from the wave function of maximum basis size (N=675;A=15) are reported in Tables 2–4.It is observed that as the plasma screening length (D) decreases,the two-electron energy levels are pushed towards the continuum.Such behaviour is quite consistent with the fact that the screened Coulomb potential becomes more and more positive with respect to the decrease in plasma screening length (D).Moreover,Tables 2–4 show that for all the ions the singlet states are more bound than the triplet states from low to moderate plasma screening.At high screening (i.e.at low values of screening lengthD),we see that the singlet and triplet states become exactly or nearly degenerate.As the plasma screening increases,the two-electron energy levels become largely affected by the continuum embedded states through configuration interactions.At very high screening region,the energy values of two-electron states come very close to the one-electron continuum and tend to merge into the 2pthreshold of the respective one-electron system.

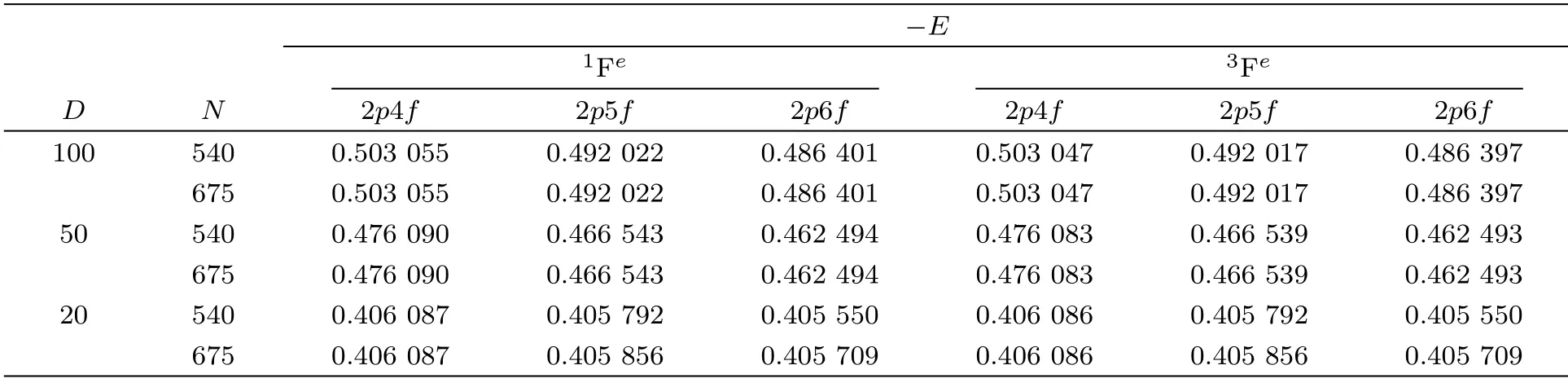
Table 1 Energy eigenvalues (−E) for the 2pnf(n=4–6) 1,3Fe states of He for different number of terms N in the basis set with respect to different Debye screening length (D).All quantities are given in a.u.

Table 2 Variation of energy eigenvalues (−E) for the 2pnf (n=4–6) 1,3Fe states of He and 2s,2p states of He+ w.r.t.the Debye screening length (D).All quantities are given in a.u.

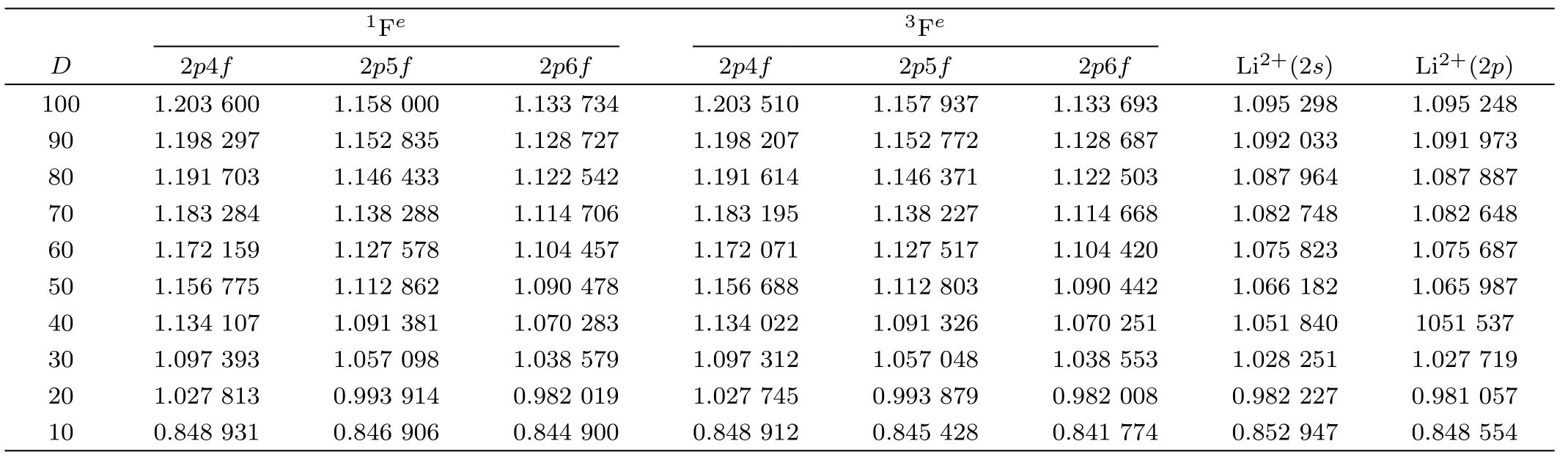
Table 3 Variation of energy eigenvalues (−E) for the 2pnf (n=4–16) 1,3Fe states of Li+ and 2s,2p states of Li2+ w.r.t.the Debye length (D).All quantities are given in a.u.

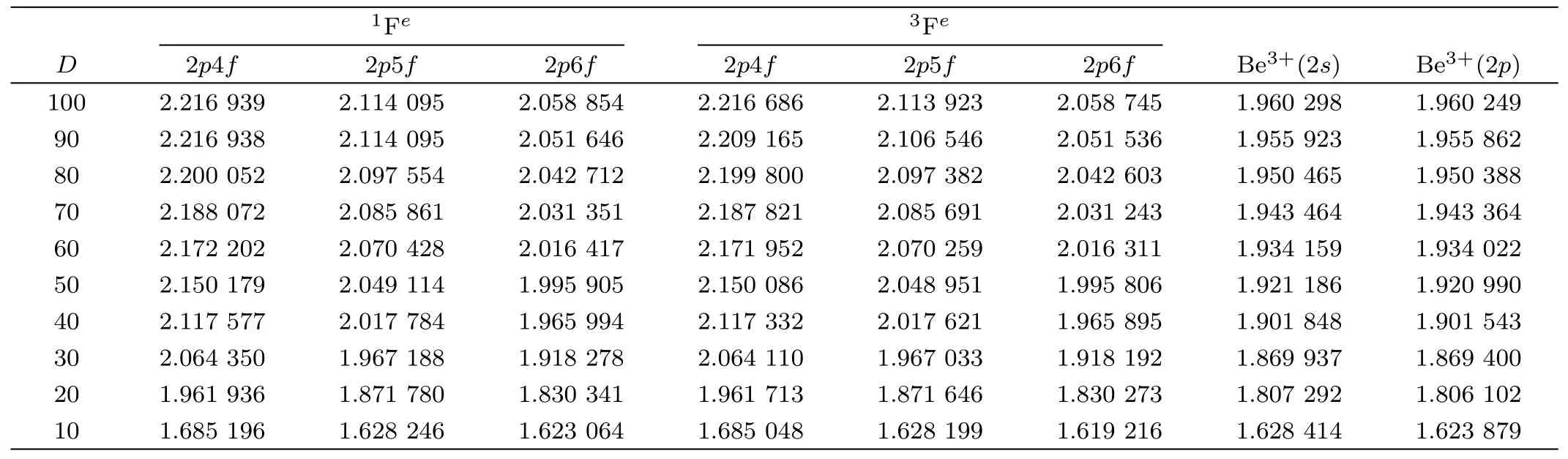
Table 4 Variation of energy eigenvalues (−E) for the 2pnf (n=4–6) 1,3Fe states of Be2+ and 2s,2p states of Be3+ w.r.t.the Debye screening length (D).All quantities are given in a.u.

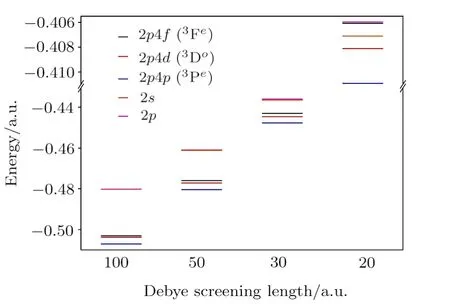
Fig.1 Relative positions of 2p4f (3Fe),2p4d(3Do)and 2p4p (3Pe) energy levels of He and 2s,2p levels of He+in different plasma conditions.

The 2sand 2pthreshold energies of respective oneelectron atoms are also included in Tables 2–4 for a comprehensive analysis of the position of two-electron energy levels.The departure from Coulomb potential facilitates the removal ofl-degeneracy in the one-electron atoms and it is evident that the 2slevel remains more bound compared to the 2plevel asDdecreases.Figure 1 illustrates the comparative behavior of different doubly excited triplet 2p4p(Pe),2p4d(Do) and 2p4f(Fe) states below He+(2p) threshold.The energy values of 2p4p(3Pe) and 2p4d(3Do) states of helium,immersed in WCP environment have been taken from Refs.[20]and[21]respectively.In Fig.1,we have shown the position of triplet 2p4p,2p4d,2p4fenergy levels of helium along with the 2sand 2pthresholds of He+at different plasma screening strength.We note that at low screening regions when the system is almost equivalent to a free system,the one-electron 2sand 2plevels are merged on each other due to theirl-degeneracy.These levels are split whenl-degeneracy is sufficiently lifted at a higher screening in presence of plasma environment which is evident from the diagram.It is seen from Fig.1 that the 2p4p(3Pe) and 2p4d(3Do)states always lie below both the 2sand 2pthresholds of He+,but the 2p4f(3Fe) level crosses the 2sthreshold of He+when the plasma screening length (D) is sufficiently small.Hence,at a low value ofD,the 2p4f(3Fe) level of helium merges to the one-electron continuum.

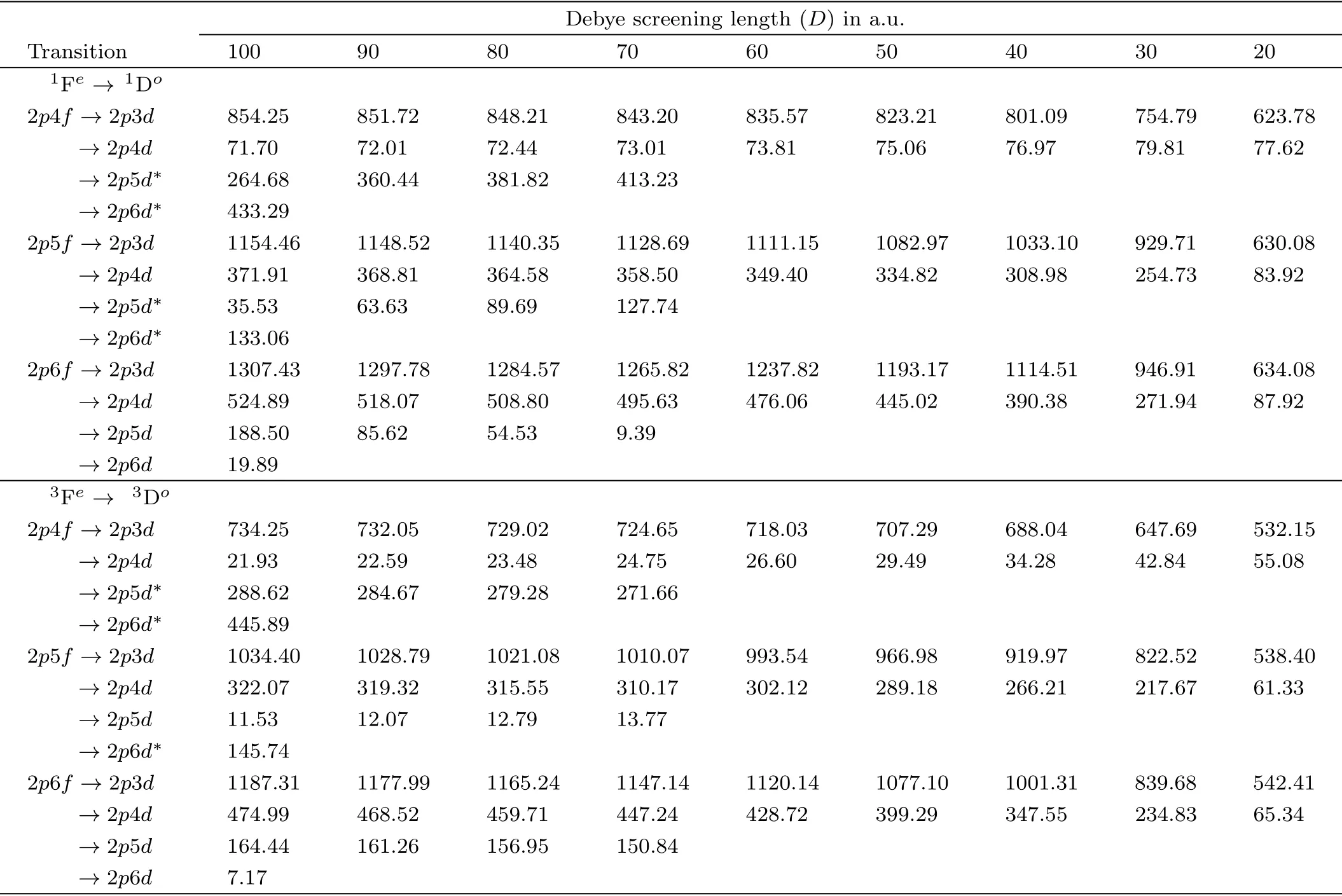
Table 5 Absolute values of the 2pnf(1,3Fe) →2pn′d(1,3Do)(n=4–6;n′=3–6) transition energies (in meV) of plasma embedded He below the He+(2p) threshold under Debye screening.

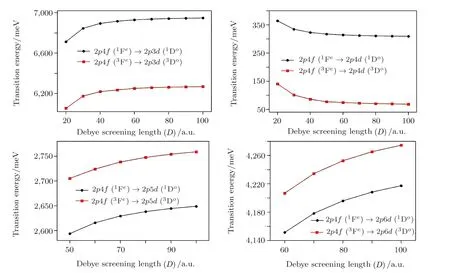
Fig.2 Variation of transition energies (meV) for 2p4f (1,3Fe) →2pnd(1,3Do) transitions (n=3–6) of Be2+ in presence of weakly coupled plasma.

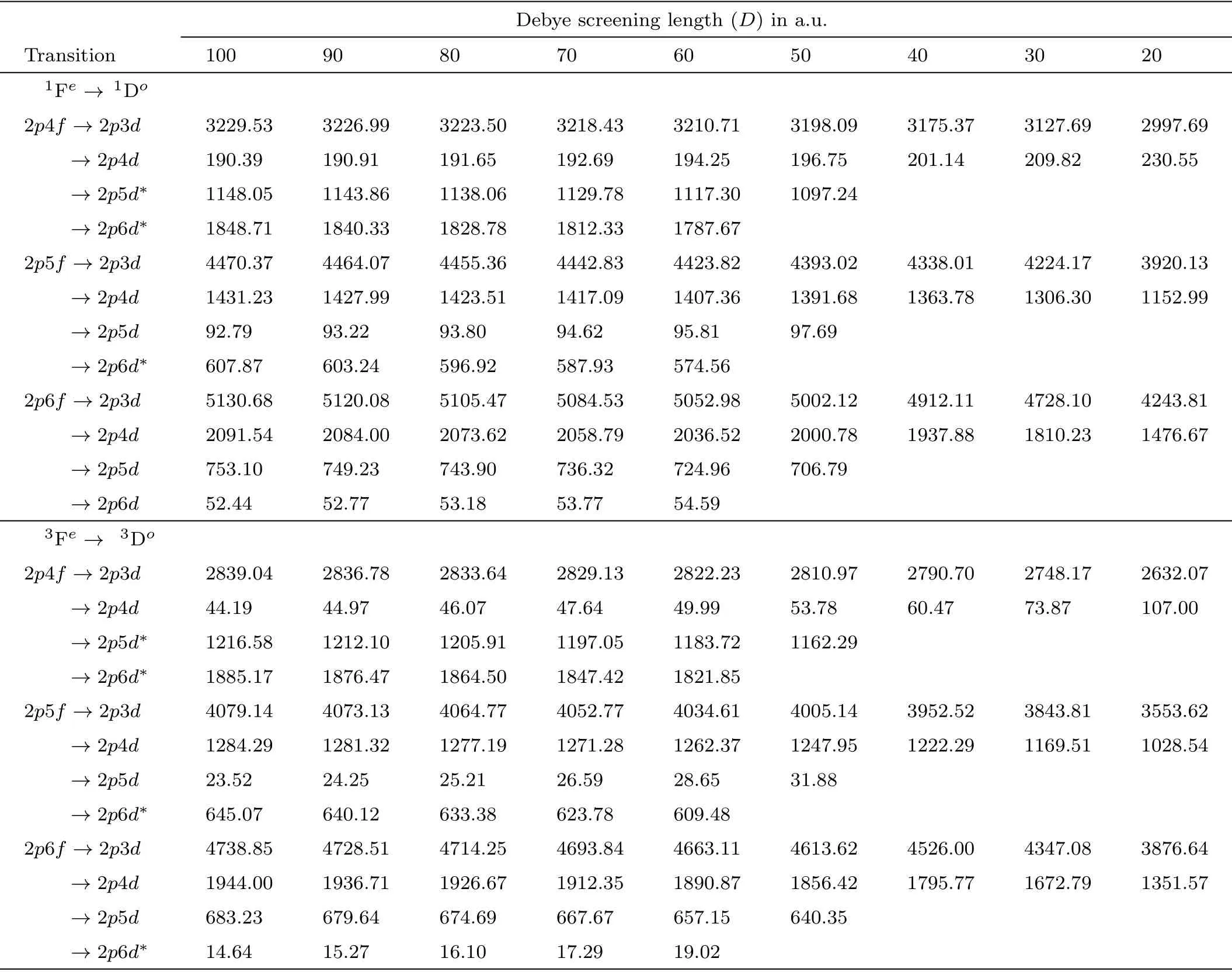
Table 6 Absolute values of the 2pnf(1,3Fe) →2pn′d(1,3Do)(n=4–6;n′=3–6) transition energies (in meV) of plasma embedded Li+ below the Li2+(2p) threshold under Debye screening.

We have also estimated the energy (in meV) corresponding to the

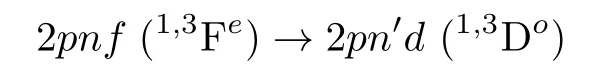
transitions (n=4–6;n′=3–6) for different two-electron atoms (Z=2–4) embedded in WCP environment.The 2pn′d(1,3Do) energy values are taken from Sahaet al.[21]and the results are exhibited in Tables 5–7 forZ=2–4 respectively.We mention that the absolute values of the difference between the position of the energy levels are given.The sequence for transition we maintain in the table is 2pnf →2pndwhereas in all the cases the 2pnfstates are not high lying.For instance,in the case of triplet states of Li+,2p4fstate lies energetically higher than 2p3dand 2p4dstates but lower than the 2p5dand 2p6dstates.We have used the conversion relation 1 a.u.of energy=27.21138 eV.[39]It is worthwhile to mention that for 2pn′d(3Do)→2p3p(3Pe) transitions in WCP environment,an initial blue shift followed by a red shift with respect to decreasing plasma screening length was reported in Ref.[21]whereas in the present case no such behavior is seen for

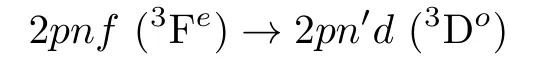
transitions.The transition energies,in a systematic manner,follow either a blue shift or a red shift for a particular transition scheme.For example,the 2p4f(3Fe)→2p3d(3Do) line forZ=4 gets a gradual red shift with respect to decreasing plasma screening length (D) and a blue shift is observed for the 2p4f(3Fe)→2p4d(3Do) of the same ion under similar conditions.Such features are evident from Fig.2 where the 2p4f(1,3Fe)→2pnd(1,3Do)transition energies (n=3–6) ofZ=4 are plotted as a function of Debye screening length (D).

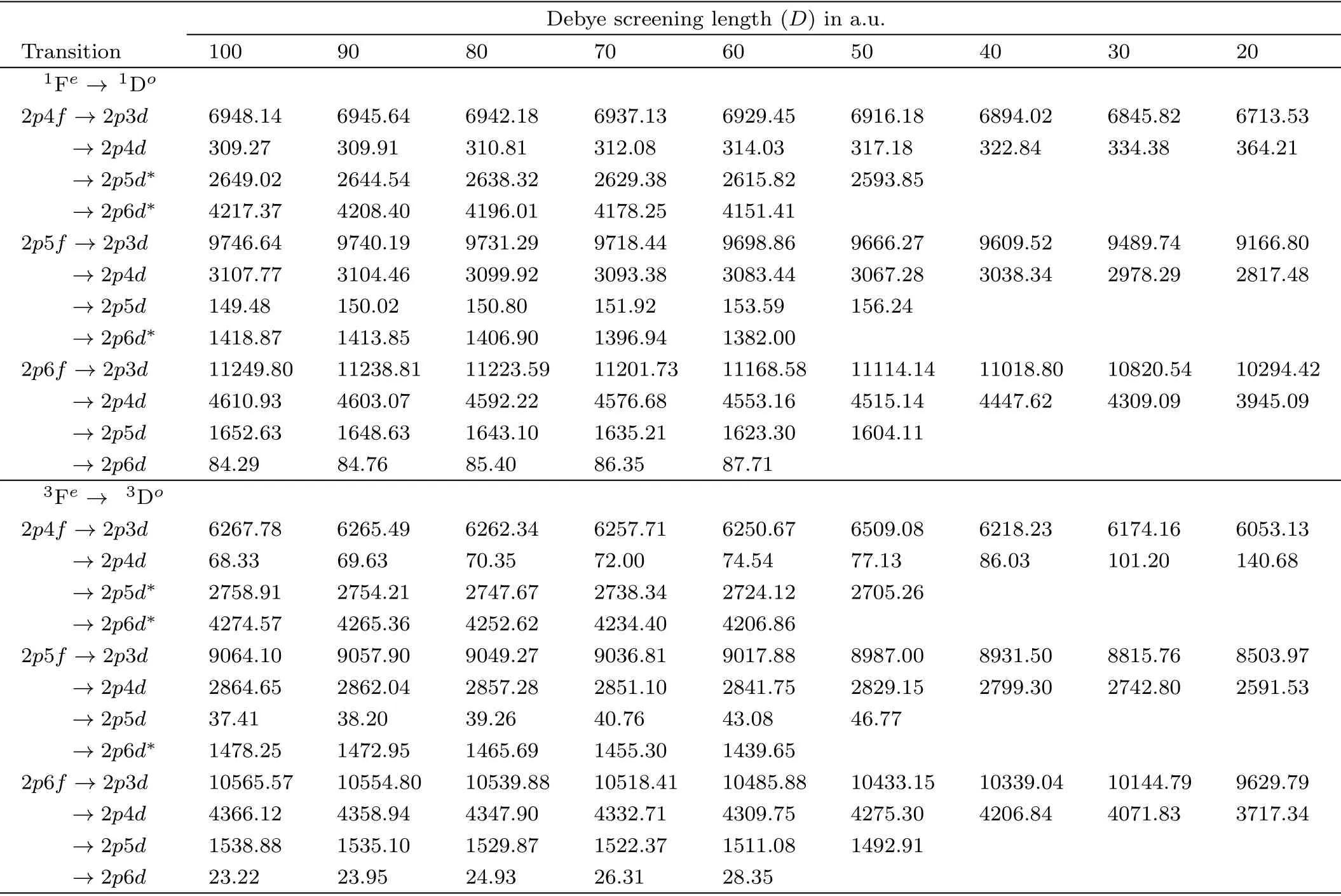
Table 7 Absolute values of the 2pnf(1,3Fe) →2pn′d(1,3 Do)(n=4–6;n′=3–6) transition energies (in meV) of plasma embedded Be2+ below the Be3+(2p) threshold under Debye screening.

4 Conclusion

We report the behaviour of doubly excited energy levels of helium-like ions in WCP environment considering screened Coulomb potential.The two-electron energy levels as well as the respective one-electron thresholds become more positive as the plasma screening length decreases.The position of different doubly excited states has been compared extensively.The transition wavelengths between doubly excited states are found to undergo a gradual blue shift or a red shift with respect to the variation in plasma screening length.Such features have implications in interpreting complex atomic spectra like those of laboratory plasma experiments or astrophysical observations.