Effects of Quantum Fluctuations on PT-Symmetric Solitons of a Trapped Bose Gas∗

Wei Qi (漆伟), Liang-Wei Dong (董亮伟), and Hai-Feng Li (李海凤)

1School of Arts and Sciences,Shaanxi University of Science and Technology,Xi’an 710021,China

2School of Science,Xi’an Technological University,Xi’an 710032,China

Abstract Considering the quantum fluctuation effects,the existence and stability of solitons in a Bose-Einstein condensate subjected in a PT-symmetric potential are discussed.Using the variational approach,we investigate how the quantum fluctuation affects the self-localization and stability of the condensate with attractive two-body interactions.The results show that the quantum fluctuation dramatically influences the shape,width,and chemical potential of the condensate.Analytical variational computation also predicts there exists a positive critical quantum fluctuation strength qc with each fixed attractive two-body interaction g0,if the quantum fluctuation strength q0is bigger than qc,there is no bright soliton solution existence.We also study the effects of the quantum fluctuations on the stability of solitons using the Vakhitov-Kolokolov(VK)stability criterion.A robust stable bright soliton will always exist when the quantum fluctuation strength q0belongs to the parameter regimes qc ≥q0>0.

Key words: Bose-Einstein condensate,PT-symmetric solitons,quantum fluctuations

1 Introduction

Isolated quantum systems are governed by unitary dynamics and described by Hermitian Hamiltonians,yet the interaction with the environment often plays an important role in studies of ultracold atoms,leading to gain or loss of particles.In the mean-field approximation of the Gross-Pitaevskii (GP) equation,the necessary particle gain and loss can be described by imaginary potentials,rendering the Hamiltonian non-Hermitian.[1−2]The particle in- and out-coupling were compared to many-particle calculations justifying their use in mean-field theory.[3−4]In 1998 Bender and Boettcher[5]discovered that non-Hermitian Hamiltonians can support stationary solutions if they arePTsymmetric.Based on this,PTsymmetry is applied to the nonlinear GP equation to describe a dilute Bose-Einstein condensate (BEC).[6]PTsymmetry implies the complex potentialV(x) contained in GP equation satisfies the condition:V(x)=V∗(−x).In such a system the imaginary part of the potential represents the in- and out-coupling of particles into or from an external environment.Many interesting nonlinear phenomena have been recovered in thisPT-symmetric BEC system.For example: NonlinearPT-symmetric quantum systems have been discussed for BEC described in a two-mode approximation;[7−8]the studies of the nonlinear quantum dynamics in aPTdouble well,[9]vortices in BEC with aPT-symmetric potential.[10]Meanwhile,PTsymmetry has found applications in several areas,it has been recently recognized that optics can provide a fertile ground wherePT-symmetric concepts can be fruitfully exploited.[11−13]And some interesting works aboutPT-symmetry-induced high-sensitivity refractive index sensors in optical solid state materials,such as coupled gain-loss microcavities have been reported.For example,a side-coupled cavity array structure has recently been explored in aPT-symmetric context for sensor applications.[14]

We know that in cold atomic systems,interactions also play a key role in its nonlinear dynamics properties.Except in the limit of weak interactions,where a mean-field approach is often sufficient,theories for interacting systems dominated bys-wave scattering length.Recently,it was pointed out that quantum fluctuations can stabilize a dipolar BEC[15−19]and Bose-Bose mixture.[20−21]Furthermore,a quantum droplet can be formed,which would otherwise collapse under attractive mean-field forces.Though tuning the atom numbers and interactions in a Bose-Bose mixture to cancel mean-field interactions completely,a novel approach to studying quantum fluctuations has been presented in Ref.[22].Moreover,it is shown with the help of quantum fluctuations,a supersolid phase can occur in dipolar BEC.[23]

Bright solitons and quantum droplets are two distinct bound states in BEC.Solitons require the gas to remain effectively one-dimensional.[24−25]In contrast,droplets are three-dimensional solutions that exist even in free space.[26−27]Recently,considering the quantum fluctuations,the static and dynamic properties of a trapless 1D BEC have been carefully studied.[28]However,combing the particles gain and loss mechanisms,how the the quantum fluctuations affect the existence and stability properties of the solitons is still absent.Our results show that the quantum fluctuations can dramatically influence thePT-symmetric soliton’s localization and stability properties.

The paper is organized as follows.In Sec.2,we present the physical models.In Sec.3,variational approach suitable for non-Hermitian systems is presented.In Sec.4,we discuss the effects of quantum fluctuations on the density profile,width and chemical potential of the solitons.Meanwhile,using Vakhitov-Kolokolov (VK) stability criterion analytical,the effects of quantum fluctuations on the solitons stability properties are presented.In Sec.5,we make our main conclusions.

2 Theoretical model

We consider a BEC with two-body and quantum fluctuation effects trapped in aPTsymmetry potential,the condensate wave function following modified GP equation:[22,29−30]

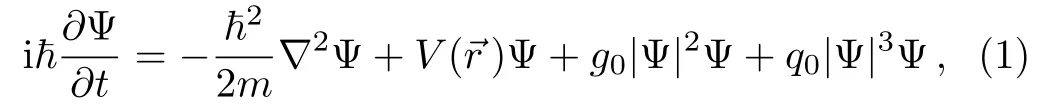
we rescale the wave function,space and times as follows:[32]

We will continue to usetinstead ofτ,and we drop the tildes for simplicity.The dynamics of the cigar-shaped condensate can be governed by a quasi-1D GP equation,which have the dimensional form:

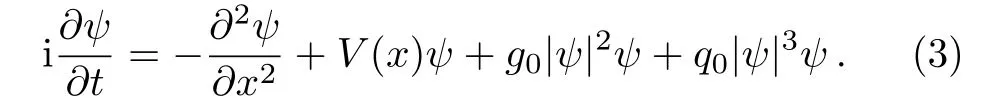
In Eq.(3) we takeV(x) to be complex valued andPTsymmetric,i.e.,possessing a symmetric real part and an antisymmetric imaginary part.The potential has the formV(x)=VR(x)+iVI(x).We choose a Gaussian-shaped potentialVR=−Vrexp(−x2) as the real part ofPTpotential.Such trap can be implemented using optical dipole traps.The imaginary part is chosen as a Gaussian multiplied byx,expressed asVI=−Vixexp(−x2).Figure 1 depicts the real part and the imaginary part ofV(x),the imaginary part represents the gain-loss mechanisms.

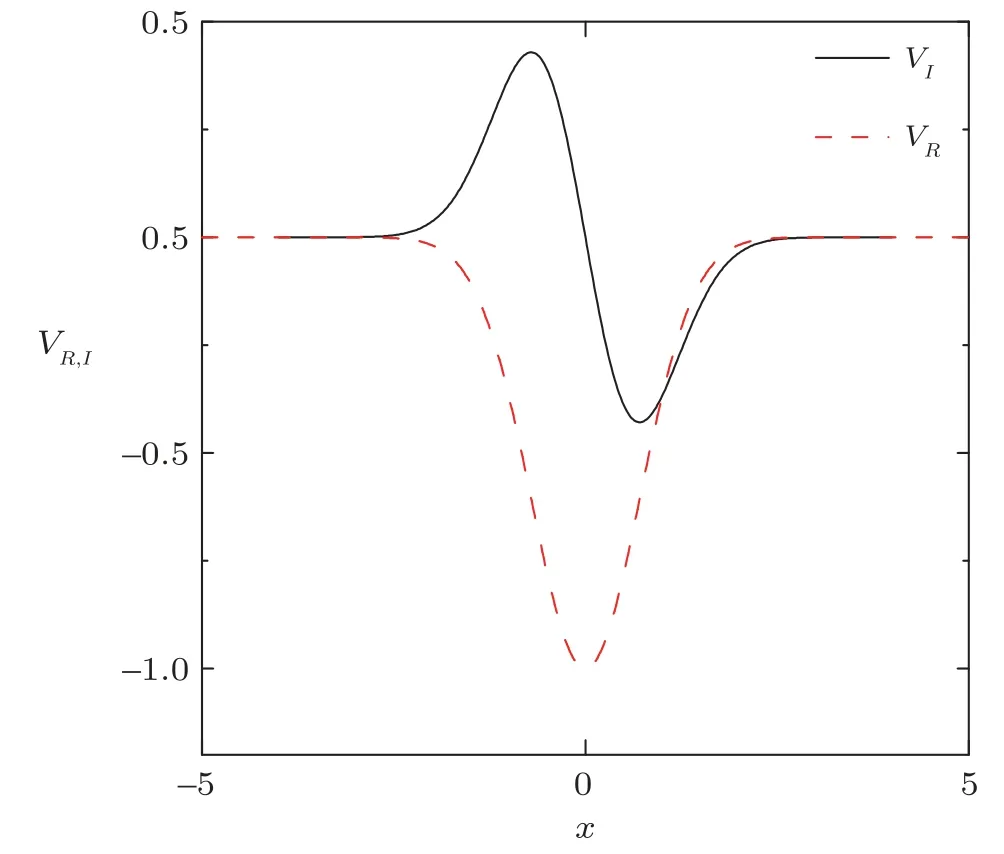
Fig.1 (Color online)The transverse profiles of the real and imaginary part of the potential V(x),the black solid line represents the imaginary part,the red dotted line is for the real part,with Vr=Vi=1.

3 Variational Approach

We are interested in devising a variational principle to obtain the equation of the wave function for the GP equation with a complex potential.However,the complexity of the potential makes the problem nonconservative.Here,we use the variational approach developed for dissipative systems.Inserting the ansatzψ=ϕ(x)exp(−iµt) into Eq.(3),we get

The Lagrangian for the conservative part,corresponding to the left-hand side of Eq.(4),is

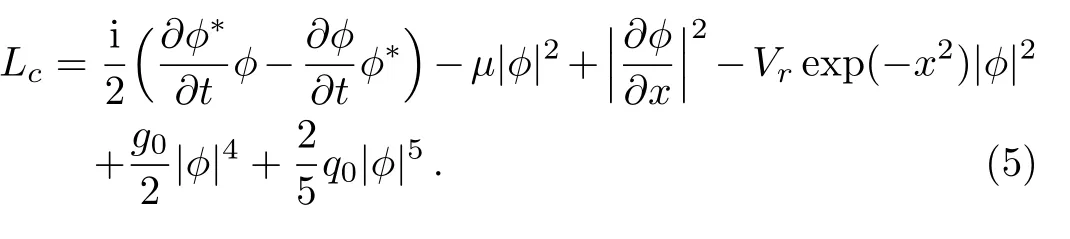
To apply the variational approach,we choose a trial solution with the nonzero phase associated withPTsymmetric stationary states:

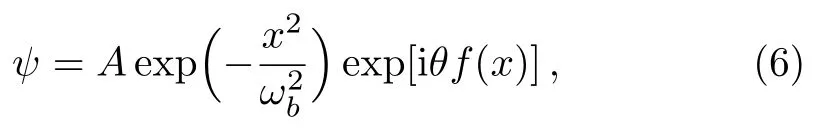
whereAcorresponds to the condensate amplitude supposed to be real,ωbis the width of the soliton,θis the amplitude of the phase profile,andf(x)is the phase distribution alongx.The particle number of soliton is defined asInserting Eq.(6) into Eq.(5),we get the following Lagrangian:

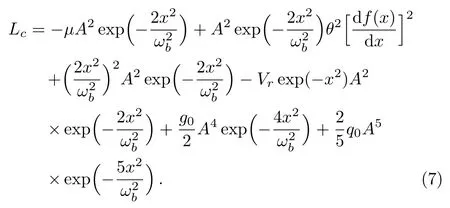
From Eq.(7),we can obtain the following reduced Lagrangianas

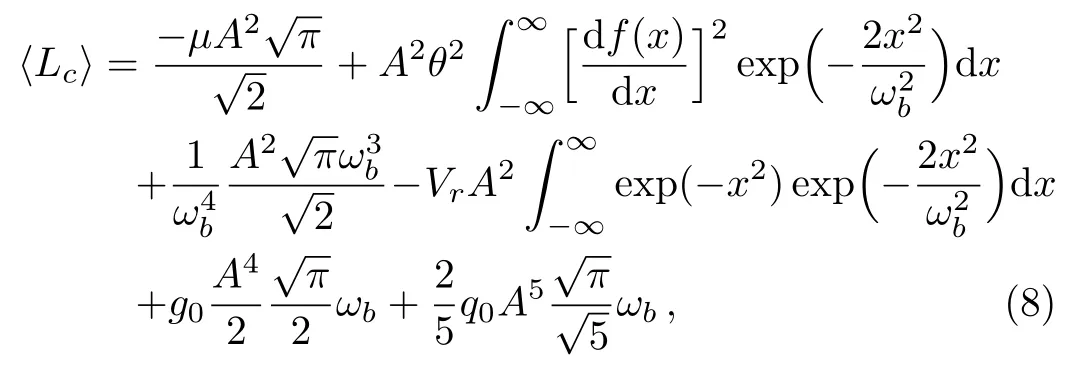
Eq.(8) can be further simplified and be rewritten in the term of particle numberN,obtaining

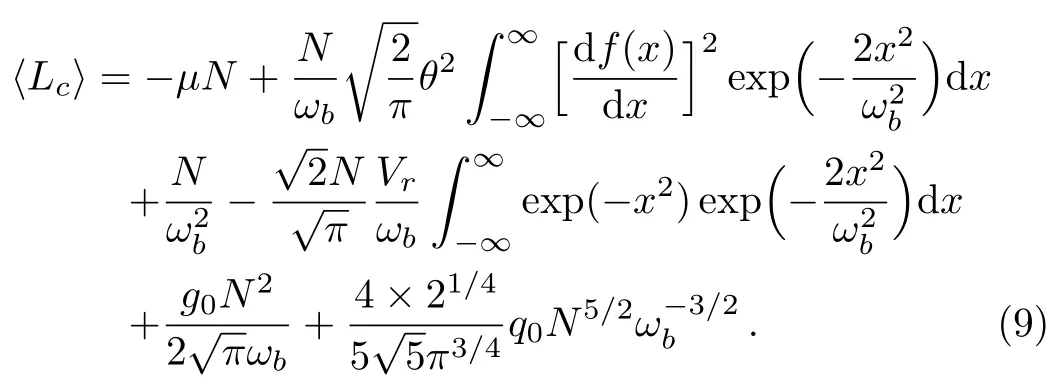
The last two terms on the right-hand side of Eq.(9)depend on the square and 5/2 power-law of the particle numberN,stemming from the two-body interactions and quantum fluctuations respectively.Using the standard variational approach for systems with dissipative terms can be modified as[29,33]

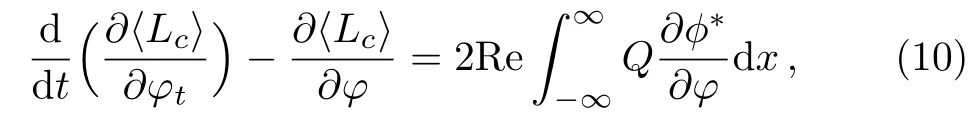
whereφ=N,ωb,θ.WithQ=iVI(x)ϕrepresenting the gain-loss of particle from environment.

Choosingφ=N,from Eq.(10) we can obtain an explicit expression for the chemical potentialµas

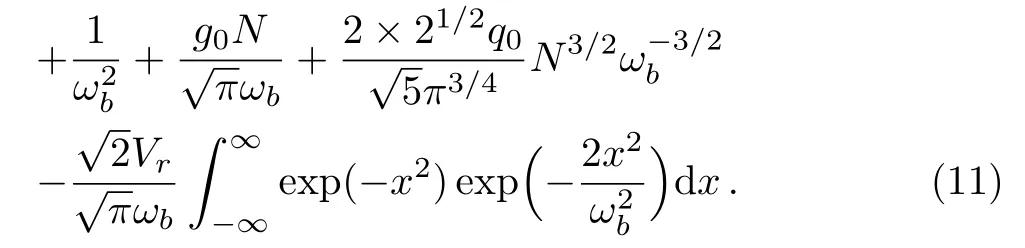
The first term on the right-hand of Eq.(11)stems from the influence of the phase profileθf(x) on the nonlinear eigenvalueµ.The second term stems from the dispersive spreading.The third and forth terms originate from twobody interaction and quantum fluctuation effects,respectively.It is clearly shown that they have competition relationship between two-body interactions and quantum fluctuations on chemical potential.The last term in Eq.(11)accounts for the contribution of the linear trapping potentialVR.

Secondly,when we chooseφ=ωb,from Eq.(10) we obtain

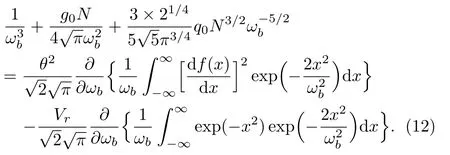
The left-hand side of Eq.(12) states the competition among dispersion of the particles(first term),two-body interactions(second term),and quantum fluctuations(third term) to determine the condensate width if the trapping potential is absent.From the expression of Eq.(12),it expresses that the quantum fluctuations dramatically influence the condensate width.The first term on the righthand of Eq.(12) arises from the inhomogeneous phase of the soliton.While the second term of Eq.(12) in righthand accounts for the influence of the linear trapping potential on the condensate width.

Finally,the equation forθis obtained by choosingφ=θ,from this we obtain

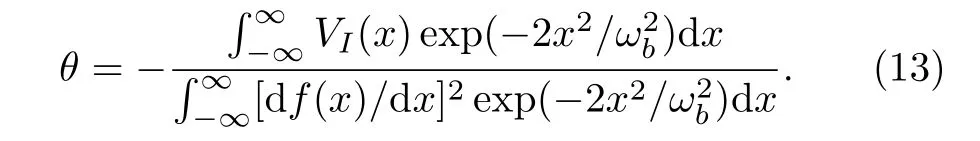
From Eq.(13),we can see that the phase of the soliton is immune from atomic interaction.For purely real potentials (VI=0),stationary solutions feature a flat phase profile acrossx.

In the following,using the variational results,we focus on how the quantum fluctuations influence on the properties of soliton.For mainly investigating the effects of quantum fluctuations on bright solitons properties,we will be interested in the particular case of two-body interactiong0=−1.

4 Discussion

In our variational analysis,we choosef(x)=tanh(x)into Eq.(6) reasonable as discussed in Ref.[34].From Eqs.(11),(12),and (13),we can get the soliton’s chemical potentialµ,normNand phase profileθ.Variational analysis is also able to predict the soliton existence,for a fixed two-body interaction,there exists a positive critical quantum fluctuation strengthqc,ifq > qc,the soliton is not able to existence.We can safely get the conclusion that a relative larger quantum fluctuation can destroy the bright soliton in a BEC.For example,if we chooseg0=−1 andµ=−6.3,the value of critical quantum fluctuation strengthqcis 0.12.From Eq.(12),we find that for a fixed soliton widthωb,ifq0≤0,there always exist only one particle normNand the corresponding chemical potentialµfor eachωb.However,if we choose the quantum fluctuation strength belong to the regimesqc≥q0>0,for a fixedωb,there always exist two meaningfulNand the corresponding twoµfor eachωb.That means there exist two branches of solution for the cases ofq0>0,one branch of solutions ofµandωbversusNare shown in Figs.2 and 3.They are shown the relationships ofNandωbversusNforq >0 are all similar with the tendency forq ≤0.The derivative of the particle numberNversus chemical potential(dN/dµ<0)in Fig.2,and as shown in Fig.3 with dωb/dN <0.We name this branch is “ordinary”branch.Otherwise,as shown in Figs.4(a)and 4(b),where the values of dN/dµand dωb/dNare all positive,this branch of solution is named “extra ordinary” branch.

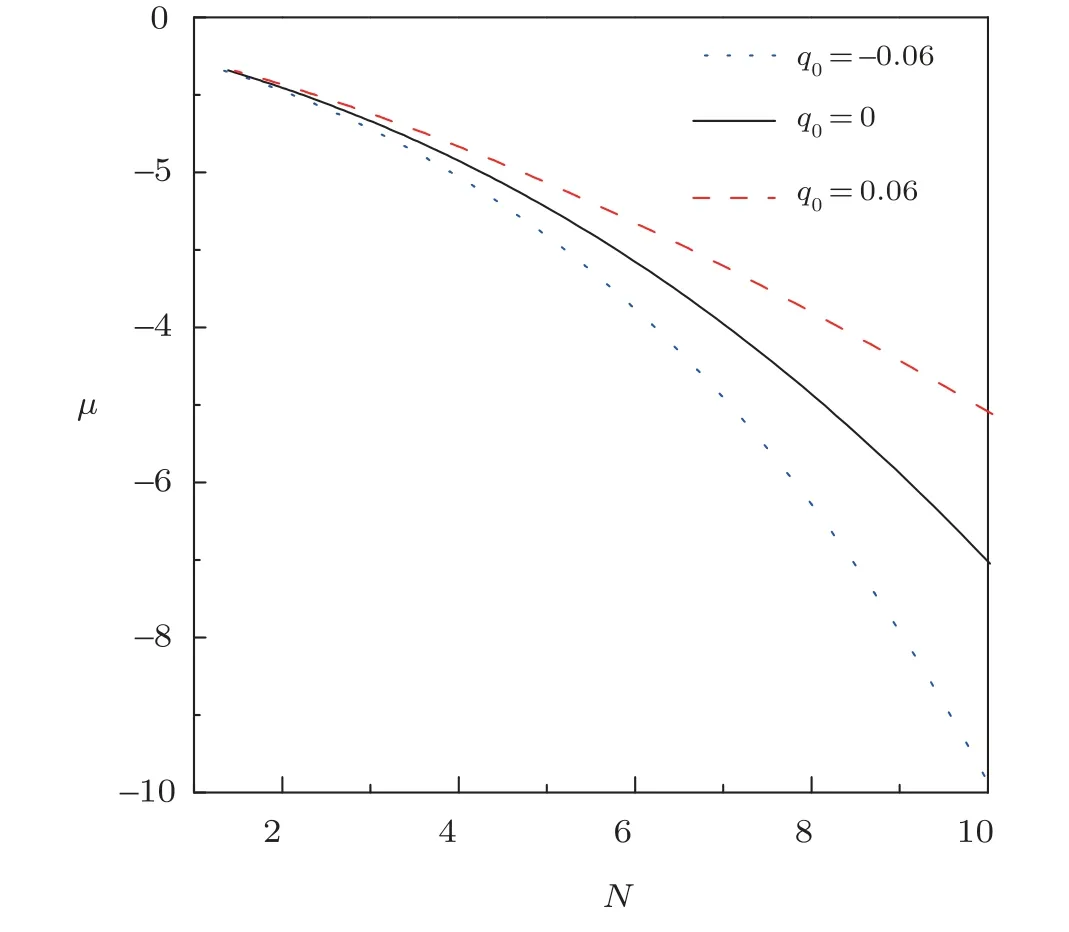
Fig.2 The nonlinear eigenvalue µ versus the particle number N with different values of q0.

For the cases ofq0≤0 or the “ordinary” branch forq0>0,the density distribution|ϕ|2of fundamental solitons with different quantum fluctuation strength (q0) are shown in Fig.5,it is shown that a slightly quantum fluctuation can change the solitons’profile dramatically.Following theq0change from negative to positive,the amplitude of the soliton becomes larger and larger.

The behavior of the chemical potentialµversus the particle numberNforq0≤0 and the “ordinary” branch ofq0>0 are plotted in Fig.2.It is shown that for a smallN,the nonlinear eigenvalueµmatches very well with differentq0.However,tending to diverge as the particle number is increased.For a relative biggerN: with the positive quantum fluctuation (red-dashed line in Fig.2)can enlarge the chemical potentialµcompared with without quantum fluctuation (black-solid line in Fig.2); the negative quantum fluctuation can reduce the chemical potential (blue dotted-line in Fig.2).From Fig.3,we can see the behavior ofωbis similar.For smallN,the effect of the quantum fluctuation on beam width can be negligible.Following the particle normNbecomes larger,the effect of quantum fluctuation onωbis obvious.

Fig.3 Soliton width ωb versus the particle number N with different values of q0.

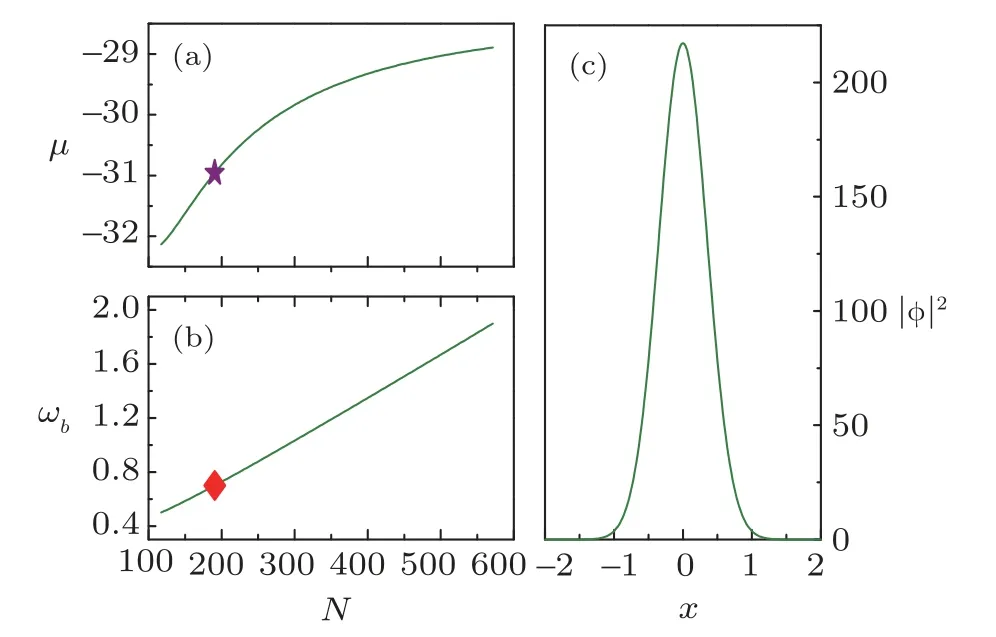
Fig.4 The nonlinear eigenvalueµ(a)and the soliton width ωb (b)versus the particle number N for the“extra ordinary”branch with q0=0.06 and g0=−1.The corresponding soliton profile (c) is plotted with the parameter marked in (a)and (b).

In Figs.4(a) and 4(b),it is shown the relationship between the chemical potentialµand widthωbversus the particle numberNfor the “extra ordinary” branch withq0>0.The very localized soliton density profile is plotted in Fig.4(c),the corresponding parameter is marked in Figs.4(a)and 4(b).It is clearly shown that in this“extra ordinary” branch,following the increase ofN,the chemical potentialµis growing nonlinear withN.However,the soliton’s width is increasing approximately linearly with the increasing ofN.And the corresponding robust soliton contains much largerNas clearly shown in Fig.4(c).

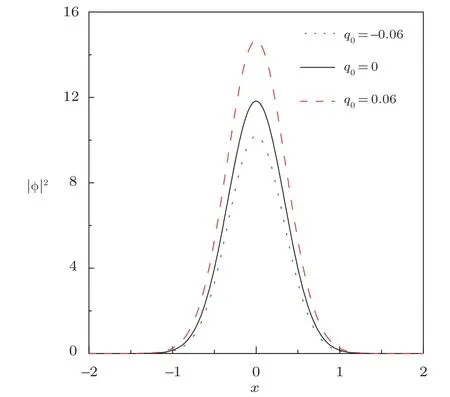
Fig.5 Bell soliton density profiles versus x obtained from variational analysis.Waveform for µ=−7.08.

Note that stability of the localized modes in nonlinear system is a very important issue.In this section,we shall focus on the stability ofPT-symmetric solitons.The Vakhitov-Kolokolov (VK) stability condition ensures the stability of solitons for the 1D local GP equation.[35]The VK condition determines the stability of the solitons based on the sign of particle number versus chemical potential graph for bright solitons.If dN/dµis positive,then the corresponding soliton is stable,otherwise,the soliton is unstable.Recently,the VK condition can also be extended to nonlinear Schrödinger equations in complex external potentials to predict the domain of stability.[36−38]For the cases ofq0≤0 or the “ordinary” branch as show in Fig.2,it is clearly shown that dN/dµis always negative,so the corresponding soliton is unstable.However,as shown in Fig.4(a),with the help of positive quantum fluctuationq0.For the “extra ordinary” branch solutions,where dN/dµis always positive.Though the Vakhitov-Kolokolov (VK) stability condition,we can get conclusion that the soliton belonging to the “extra ordinary”branch forq0>0 is always stable.Physically,due to the competition between attractive two-body interactions and positive quantum fluctuations,the repulsive force induced from quantum fluctuations can arrest the collapse and stabilize the system.A moderate quantum fluctuation can survive a robust bright soliton,but a larger positive quantum fluctuation can destroy a bright soliton.

5 Conclusion

In this work,we analyze the existence and stability of localized states of BEC with quantum fluctuations trapped in aPT-symmetric potential.Within the meanfiled framework,we find that the quantum fluctuations can dramatically influence thePT-soliton state in BEC.That means the quantum fluctuation can influence thePTsymmetric soliton’s profile,chemical potential and width.Most importantly,it is shown that with the help of positive quantum fluctuation,a robust stablePT-symmetric bright soliton which contains much large particle norms will be found.Our results may be feasible experimentally,where the real part of the PT-symmetric potential is a simple Gaussian-shaped potential,which is easily achieved.[39]To implement imaginary part which accounts for gain-loss mechanisms,a pumping scheme can be exploited as well as optical dipole traps,[40]but the loss mechanisms can be implemented shining the BEC with electron beams.[41]And the strength of two-body interaction and quantum fluctuations can be tuned using Feshbach resonance.[42]