潮流条件下的桩基冲刷深度研究
2019-07-24袁春光王义刚张义丰庞启秀侯志强
袁春光,王义刚,张义丰,庞启秀,李 鑫,侯志强
(1.交通运输部天津水运工程科学研究所 港口水工建筑技术国家工程实验室 工程泥沙交通行业 重点实验室,天津 300456;2.河海大学 港口海岸与近海工程学院,南京 210098)
针对潮流条件下桩基冲刷深度的研究主要存在以下两种观点:(1)潮流条件下由于最大流速的有效冲刷时间不足和潮流转向可能会带来泥沙的回填,因此潮流的最大冲刷深度应当比恒定流小;(2)虽然在一个潮周期内最大流速的持续时间很短,但只要潮周期数量足够多,最大流速依然是控制最大冲刷深度的主要因素,因此潮流作用下的局部冲刷应与恒定流情况一致(张景新[1])。
目前对于潮流条件下桩基局部冲刷深度的预测主要为两种方式:(1)折减系数法,将潮流冲刷结果与涨急或者落急时刻恒定流条件下的局部冲刷结果进行对比,从而得出潮流折减系数,卢中一[2], Wang Jianping[3],王佳飞[4]和李梦龙[5]等均是采用这种方法;(2)公式拟合法,根据潮流冲刷物理模型实验结果,直接进行桩基局部冲刷公式拟合,属于此类方法的研究有Sumer[6],Escarameia和May[7],韩海骞[8]和王明会[9]等。McGovern[10-12]认为潮流条件下的桩基冲刷折减系数应当与潮流流速与底床泥沙起动流速的比值有关。王冬梅[13]通过对长江口苏通大桥南、北主墩周围最大深度的测量,认为用沙波起动流速和落急最大流速分别取代单向流作用下桥墩局部冲刷计算公式中的单颗粒泥沙的起动流速和墩前流速,可以获得更准确的计算效果。
我国《中华人民共和国公路工程水文勘测设计规范》[14]和美国《桥梁冲刷估计》[15]认为受潮汐影响水域的桥墩冲刷应该按照径流和潮汐最不利组合情况下的水动力条件来预测桩墩的冲刷深度,主要是引用恒定流条件下的桥墩冲刷公式进行计算。显然,两种规范主要是从工程安全的角度提出以上方法来对潮流环境下的桥墩冲刷深度上限值进行预估,而桥墩的实际冲刷深度可能比恒定流估计值要小很多,这在工程中可能造成不必要的浪费。通过总结归纳国内外研究工作,分析潮流条件下桩基冲刷过程的机理,提出“查图法”和“微分迭代法”,提高潮流环境中桩基冲刷的预测精度。
1 流速和周期对桩基冲刷的影响
与径流相比,潮流条件的主要区别在于水深和流速是周期性变化的,对于某一个短时间段△t内,该时刻t所对应的水动力条件为流速Vt和水深ht,计算该△t内的冲刷发展过程,需要通过公式(1)来计算。
ds(t+△t)=ds(t)+((d[ds(t)])/dt)·△t
(1)

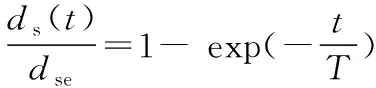
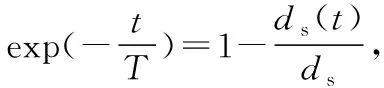
(2)
式中:T为冲刷时间尺度;D为桩基直径;δ为水流边界层厚度;s为底床泥沙比重;θ为希尔兹参数;τ为底床切应力;ρs为底床泥沙密度;ρ为水的密度;g为重力加速度;d为底床泥沙粒径。
同理对于Melville[16]清水冲刷发展公式有
(3)
式中:te为冲刷平衡时间;D为桩基直径;V为水流垂向平均流速;Vc为底床泥沙起动平均流速;h为水深。
可见潮流条件下,式(2)和(3)中的冲刷时间尺度T(或te)和ds(dse)都是随时间变化的,当某一时刻完成的冲刷深度与该时刻流速Vt和水深ht所对应的极限冲刷深度相等时冲刷停止,即公式(1)的迭代条件为ds(t)≤ds(Vt,ht)且V≥0.5Vc(V为来流垂线平均流速,满足桩前冲刷的起冲条件)。因此不同时刻水动力情况对应的极限冲刷深度和该时刻已经发生的冲刷深度是影响该时刻冲刷发展的关键。当底床泥沙组成、桩基尺寸和水流交角确定以后,影响桩基极限冲刷深度的因素主要为水流的流速和水深,根据Ettema[17]的研究水深只在一定范围内对冲刷深度有影响,超过这一范围后,即使水深增加冲刷深度也不再改变,流速是影响冲刷深度的主要因素。

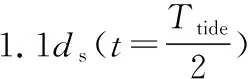
2 潮流条件下桩基冲刷计算方法
2.1 查图法
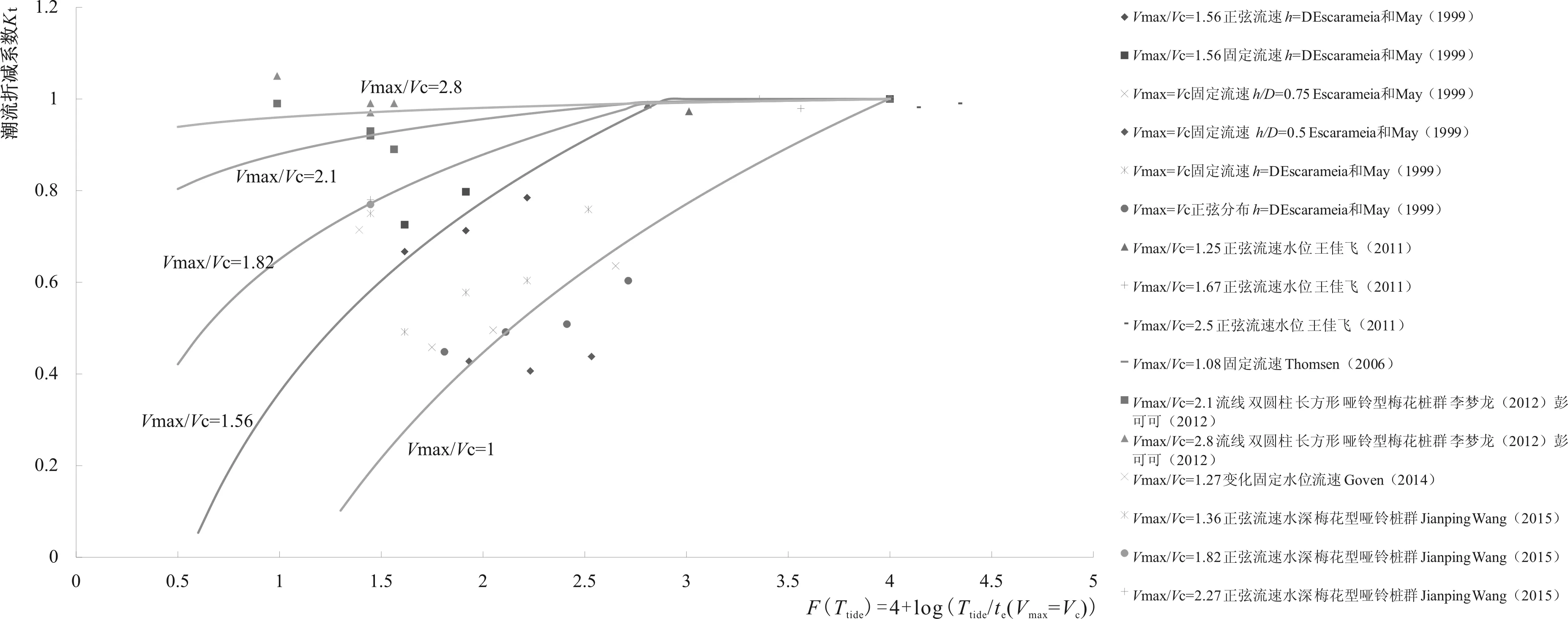
注:“固定流速”表示潮流冲刷实验只改变水流方向,流速保持固定值;“固定水位”表示实验过程水深恒定图1 潮流折减系数Kt与潮周期参数F(Ttide)和相对流速的关系Fig.1 Relationship between the tidal flow scour reduction factor Kt and tide period coeffient and relative velocity

当潮流引起的Vmax≥Vc时,查图法的具体步骤如下:
(1)根据涨落急时刻的水流条件,利用经过验证准确性较高的的恒定流桩基局部冲刷公式计算相应的最大冲刷深度ds恒定流;

(3)当Vmax≥Vc时,查图1得到潮流冲刷折减系数Kt,潮流条件下桩基局部冲刷深度
ds潮流=Kt×ds恒定流
(4)
“查图法”的优点是计算比较简便,可根据不同的工程环境任意选择最符合当地自然条件的ds恒定流计算公式,潮流冲刷折减系数Kt图来自物模实验,具有一定的可靠度。不足主要为两点,①图1的实验数据全部为Vmax≥Vc的动床情况,对于Vmax 考虑到以上提到的潮流条件下的桩基冲刷机理,由于水流条件会随时间变化,利用微分方法更能反映潮流条件下局部冲刷的发展过程。根据Escarameia和May[7]的实验成果。 (5) 当Vmax>Vc时,ds潮流=ds(t=m·Ttide=kn0·△t) (6) 当第(n+1)个时间段处于清水冲刷时,即0.5Vc 初始时刻n=0,根据以上的方式不断迭代直至冲刷深度稳定于某一个值或者在某个值上下波动为止,这个值即为潮流条件下桩基的平衡冲刷深度,具体迭代计算步骤见附录。 2-a Vmax=0.15 m/s,T=72 min,h=0.21 m,d50=0.051 7 mm(木粉)2-b Vmax=0.15 m/s,T=72 min,h=0.15 m,d50=0.051 7 mm(木粉)图2 潮流条件下桩基冲刷深度发展过程(王佳飞[4])Fig.2 The time development of local scour in tide flow 图2将积分迭代法的计算结果与王佳飞[4]实验的实测值的对比,由于模型沙选用了木粉,其起动流速按照李昌华公式[19]计算,平衡冲刷深度时采用袁春光[20]提出的半经验半理论公式计算。可见,图2-a中的计算值稍大于实测值,这与采用的恒定流平衡冲刷公式[20]拟合结果与实际冲刷深度结果之间存在一定的误差有关,总体而言,通过微分迭代法得到的潮流局部冲刷深度发展过程具有一定精度。 动床条件时,潮流引起桩基局部冲刷的折减系数Kt将随着相对流速Vmax/Vc和相对周期Ttide/te(V=Vc)的增加而增大。在对称潮流条件下,当Vmax/Vc=1时,Kt仅为0.4~0.6之间;而当Vmax/Vc≥2.1时,Kt均达到0.9以上,由于泥沙冲刷过程有很强的不稳定性,出于安全角度考虑,此时不宜再进行潮流折减计算。根据实测资料,只有当潮流相对流速Vmax/Vc<2.1时,潮流引起的桩基的局部冲刷深度才有进行折减的必要。提出了“查图法”和“微分迭代法”两种方法来计算潮流条件下的桩基局部冲刷,经过验证计算结果与实测值吻合良好。2.2 微分迭代法
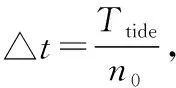
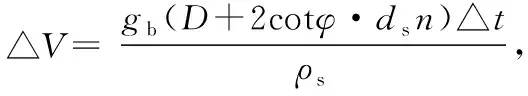


3 主要结论
