载机滚转条件下的导弹弹射分离横向位移研究
2019-07-24张士卫戚孜江
刘 浩, 周 军, 张士卫, 戚孜江
(1.西北工业大学 航天学院,西安 710072;2.中国空空导弹研究院,河南 洛阳 471009)
五代战机为了追求隐身性能,其挂装的空空导弹高密度地内埋于武器舱内并通过弹射发射实现机弹分离。为了进一步提高优作战性能,五代战机要求能在空中高速滚转条件下实现空空导弹弹射发射。美国F-22战机已基本能在90°/s的滚转速度下进行空空导弹弹射发射。对载机高速滚转状态下的导弹弹射发射分离安全性这一新的课题进行研究具有相当重要的实际工程意义。
现阶段对机载导弹的发射分离安全性研究已取得了许多重要的成果,但基本集中于载机非滚转状态下的多体发射动力学研究和气动流场对发射安全性的影响研究,对载机空中滚转条件下的发射安全性研究还鲜见报道。刘刚等[1]采用流体动力学和多刚体动力学耦合求解的方法对载机平飞状态下的空空导弹导轨式分离过程进行了数值模拟;王林鹏等[2]针对柔性接触模型计算稳定性差等问题,提出了一种能随空空导弹导轨发射装置变形的点线约束来替代结构接触的建模方法,提高导弹发射过程的计算稳定性;刘浩等[3]采用构件模态离散和拉格朗日多体动力学方程相结合的方法研究了载机俯冲拉起大过载条件下的内埋弹射分离动力学特性;薛飞等[4]在0.6 m×0.6 m的亚跨超声速风洞中开展了载机平飞状态下的内埋导弹弹射分离试验技术研究。王许可[5]针对载机平飞状态下的弹射发射俯仰角速度波动的问题,建立了某空空导弹发射机构刚柔耦合动力学模型,对导弹发射分离姿态进行了仿真。张群峰等[6]基于湍流模式的改进延迟分离涡(Improved Delay Detached Eddy Simulation, IDDES)模拟方法以及重叠网格技术,对载机平飞条件下的外挂弹射和内埋弹射的导弹分离轨迹进行了对比分析。国外学者对载机平飞状态下的发射多体动力学和发射过程的气动流场影响也进行了相当的研究[7-11],相关成果保证了机载导弹发射分离安全性。
本文基于伪坐标形式的拉格朗日法建立了载机滚转条件下的导弹弹射发射动力学仿真模型,仿真分析了弹射分离过程的导弹分离速度和横向位移,结果表明弹射分离速度正常,导弹横向位移偏大威胁发射安全性。提出对弹射机构前后链路进行刚度匹配降低导弹横向位移的新思路,仿真及试验结果表明刚度匹配法效果显著。本文也可为其它类似平面柔性机构的设计提供方法借鉴。
1 伪坐标形式的Lagrange方程建模
伪坐标形式Lagrange方程是Lagrange动力学方程在航空航天领域应用的一种改进形式,伪坐标形式的Lagrange动力学方程为[12-14]
(1)

仿真模型由载机、柔性弹射机构以及导弹三部分组成,载机坐标系原点位于载机质心,向前为X正向,向上为Y正向,Z向(横向)满足右手定则,如图1所示。
(2)

图1 弹射发射结构布局示意图
式中:rr为载机坐标到载机任一质量元矢量。
柔性弹射机构任一质量元在惯性空间的速度矢为

(3)
式中:rof为载机坐标到柔性机构任一质量元的矢量;vf为弹射机构伸展速度矢量;u为各质量元柔性变形位移。
u=Φq
(4)
式中:Φ为柔性体正则模态;q为模态坐标。
(5)
式中:rom为载机坐标到导弹质心的矢量。
载机其动能Tr为

(6)
式中:mr为载机质量,Ior为载机相对载机坐标系的惯量张量。
弹射机构由多个构件通过运动副组装而成,弹射机构的动能Tf为各构件之和。
式中:n为弹射机构的构件数。
Φ为构件的正则模态,则
(9)
因此对于任一柔性构件的动能Tfj为
(10)
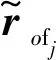
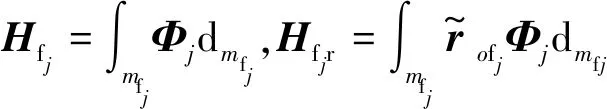
则弹射机构任一构件动能Tfj可描述为
(11)
弹射机构总的动能Tf为
(12)
式中:mf为弹射机构的总质量。
柔性弹射机构变形势能Uf为

(13)
式中:u为由弹射机构各节点变形位移构成的变形位移列阵;k为弹射机构的刚度阵。用模态坐标表示时
(14)
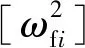
导弹动能Tm
(15)
式中:mm为导弹质量;Iom为导弹对载机坐标系的惯量张量;rom为坐标系原点到导弹质心的向量;vm为导弹伸展速度矢量。
本文假设载机处于水平直线飞行状态时进行滚转发射导弹,此状态下重力势能对导弹发射过程的影响较小,因此可忽略重力势能影响。则拉格朗日函数为
L=Tr+Tf+Tm-Uf
(16)
代入式(1)可得到载机滚转条件下弹射机构的弹射分离动力学方程

(17)

从式(17)可知:载机的平动、滚转以及弹射机构的变形之间存在耦合效应。
2 战机滚转发射动力学仿真分析
考虑到系统模型的复杂性,采用有限元法+拉格朗日动力学方程相结合的方法进行仿真模型建立[15-16]。利用有限元软件对弹射机构的各柔性构件分别进行模态离散化,并在多体动力学软件中根据弹射机构运动副约束条件组装载机、弹射机构各构件和导弹,最终建立载机滚转条件下的导弹弹射分离动力学仿真模型。对战机水平直线飞行且90°/s滚转条件下的弹射分离动力学特性进行仿真分析,发射平面为铅锤面,重点分析导弹弹射分离速度和导弹横向位移。滚转时角加速度和弹射面与铅锤面夹角对发射过程也有一定的影响,但影响相对较小,限于篇幅本文暂不考虑。
图2为导弹的弹射分离速度曲线,横坐标为弹射时间,纵坐标为导弹分离速度。由图2可知,导弹的弹射速度逐渐增大,在8.3 m/s导弹与弹射机构分离,整个弹射过程持续约0.12 s。理论研究和工程实践表明,当导弹弹射分离速度大于等于7.6 m/s时,导弹能够安全穿越载机周围的复杂气动干扰层。由此可见,滚转条件下导弹弹射分离速度正常。由于弹射发射导弹时,导弹相对于载机存在较大的相对分离速度,且由于载机处于高速滚转状态,因此导弹将受不可忽略的科氏力作用,该科氏力垂直于弹射面,将导致弹射机构在高速弹射过程中产生横向变形位移。

图2 导弹弹射分离速度
图3为弹射机构对导弹前/后挂点约束处的横向位移,由于导弹质心到前后挂点距离差别较大造成前后挂点Z向位移不一致,其中4 mm为导弹与发射机构分离时刻前挂点处横向位移,10 mm为导弹与发射机构分离时刻后挂点处横向位移,可看出前/后挂点处横向位移相差较大,达到6 mm。
图4为导弹尾部的横向位移。从图4可知,在导弹与弹射机构分离时刻导弹尾部横向位移达到27mm。究其原因:由于弹射过程中机构前后挂点横向位移相差较大,达到6 mm,导致导弹产生了较大偏航角,由于导弹尾部离挂点较远,因此导弹尾部位移较大,达到27 mm,影响了导弹发射分离姿态,并可能造成导弹尾部与邻近导弹的相互碰撞。
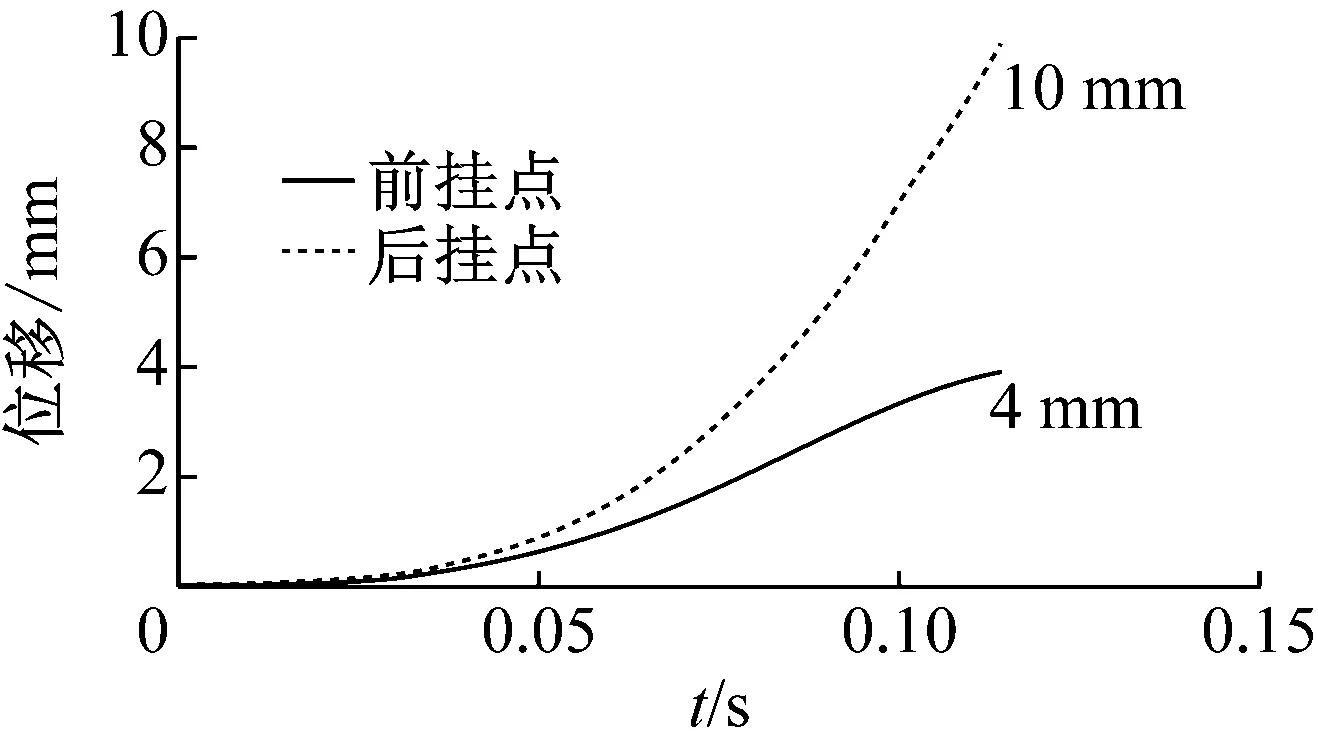
图3 前/后约束点Z向位移

图4 导弹尾部横向位移响应
3 弹射过程横向位移抑制研究
导弹的横向位移将导致高密度内埋挂装的导弹之间的相互碰撞,严重影响到发射安全性,另一方面,导弹横向位移也将影响到导弹的发射分离姿态,进而影响导弹的初始弹道。现阶段针对机构伸展过程中的柔性变形问题,其解决的主要思路有:① 提高机构的刚度;② 采用主动控制法。对于机载内埋弹射发射系统,其有严苛的轻量化设计要求,且由于高密度挂装要求,其结构设计可用空间相当紧张,因此提高机构刚度法在工程中受到极大限制;对于主动控制法,由于导弹弹射发射过程时间很短(小于0.15 s),且机构产生的弹射作用力达数吨,机构柔性变形显著,主动控制法在工程上也难以实施或成本太高。
针对此难题,本文提出对机构前后链路进行刚度匹配设计,该方法致力于降低弹射机构对导弹的前/后挂点的横向位移差,使导弹减小由于机构横向位移差导致的偏航角,从而降低导弹尾部的最大横向位移。
图5和图6为机构Z向刚度匹配设计示意图。由图5可知,其刚度匹配环节设计于弹射机构对导弹的前挂点约束处(即离导弹质心较远的挂点约束处)。刚度匹配环节采用片簧替换Z向刚性约束,如图6所示。当导弹前吊挂受Z向力时,片簧将产生压缩变形,导弹前吊挂相对弹射机构安装座能产生Z向相对位移。
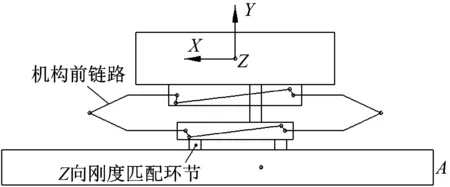
图5 弹射机构刚度匹配设计示意图
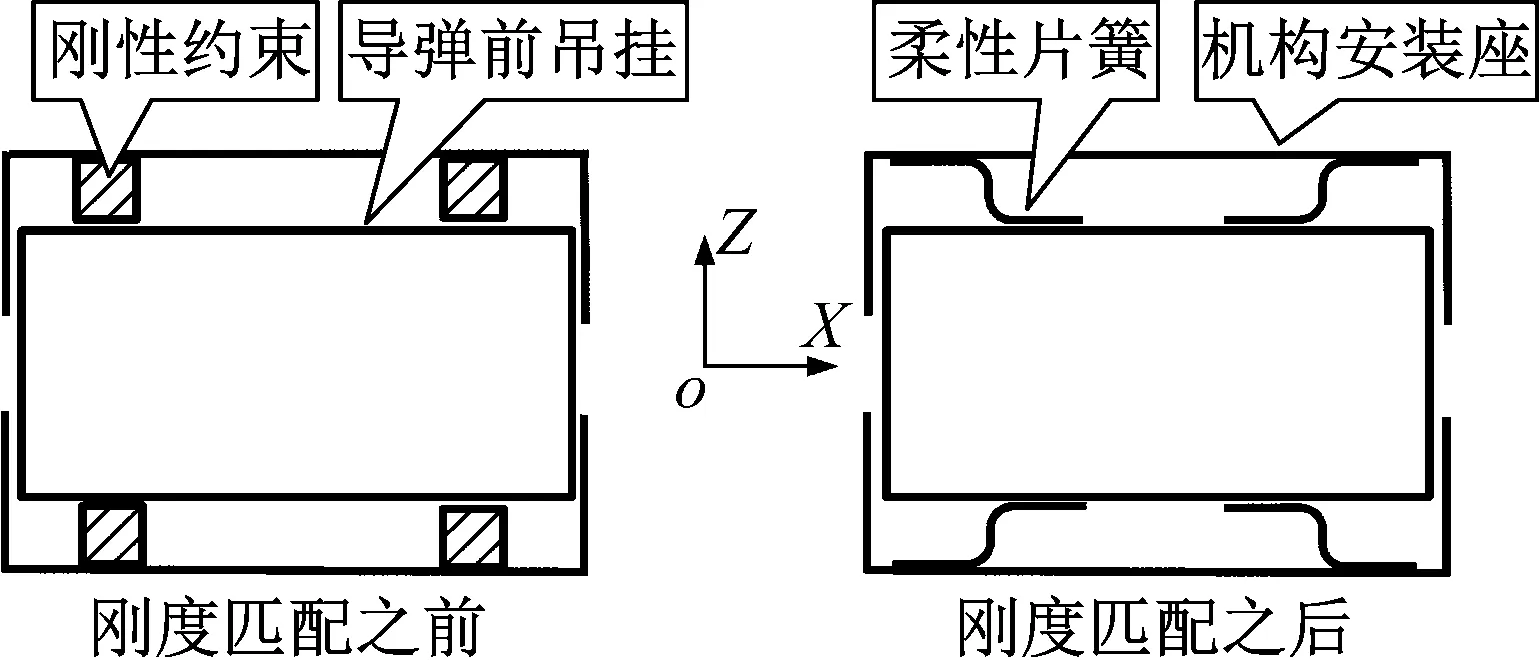
图6 刚度匹配设计方案示意图
刚度匹配设计抑制导弹尾部横向位移的原理:导弹质心离弹射机构后挂点比前挂点要近得多,在Z向科氏力作用下,机构后挂点受力将明显大于前挂点,导致后挂点处由于机构变形产生的Z向位移也大于前挂点,因此造成导弹产生较大偏航角,从而使导弹尾部横向位移过大。在机构前挂点引入刚度匹配环节设计后,在科氏力作用下,前挂点由于刚度变弱,其变形将增大,因此前后挂点变形差将减小,从而使导弹偏航角减小,最终实现导弹尾部横向位移的抑制。
刚度匹配环节片簧的刚度值设计方法,其共分为2个阶段:① 预估;② 进行发射过程整体动力学仿真。
1) 预估:为了减少发射过程的整机数值仿真的计算次数和计算量,需要初步确定刚度匹配环节的大致刚度,其思路是机构前、后链路的刚度与质心到前后挂点的距离成反比。其刚度值预估方法为
即KQ+F∶KH=LH∶LQ
式中:KQ为机构前链路Z向刚度;KF为刚度匹配环节的Z向刚度;KH为机构后链路Z向刚度;KQ+F引入刚度匹配环节后前链路Z向刚度;LQ为导弹质心到前挂点距离;LH为导弹质心到后挂点距离。
事实上,弹射机构前、后链路的刚度较难准确得到,且在弹射伸展过程中前、后链路的刚度值在变化,前、后刚度比也在变化。在工程上可将弹射机构的前链路、后链路分别通过Z向加载的方式进行Z向刚度测试,通过计算Z向加载力与Z变形位移的比值求得各自Z向刚度值,加载时需要对弹射机构不同的伸展位置进行测试,并取平均刚度比值。当然,也可以分别对前、后链路分别采用有限元仿真的方式计算Z向刚度值,并通过机构不同伸展位置的刚度值求得前、后链路的平均刚度比值。
2) 整机动力学仿真:在对刚度匹配环节的刚度进行预估之后,可对引入刚度匹配环节后的机载导弹弹射发射动力学模型进行整机发射动力学仿真。通过调整刚度匹配环节的Z向刚度,使前后挂点变形差和导弹尾部位移值达到最小。
图7为采用刚度匹配设计后前/后挂点约束处在导弹弹射过程中的横向位移响应,机构前后链路刚度比为0.37。8.7 mm是前挂点处的横向位移,10.8 mm是后挂点处的横向位移,前后挂点的横向位移差2.1 mm。采用刚度匹配设计后,前后挂点横向位移差由之前的6 mm减小到2.1 mm。

图7 刚度匹配后的前后挂点横向位移
图8为采用刚度匹配设计前后的导弹尾部横向位移对比图。从图8可知,当弹射机构前后链路刚度比为0.37时,导弹尾部最大的横向位移由27 mm降低至16.7 mm,有利于导弹良好的发射分离姿态,保证了载机发射安全性。

图8 刚度匹配前后横向位移对比图
4 试验研究
对机载弹射发射装置采用刚度匹配设计后的横向位移抑制效果进行试验验证。试验方法:将弹射发射装置悬挂于发射台上,弹射发射装置下端悬挂导弹,导弹Z向采用钢丝绳方式施加拉力模拟科氏力对导弹及机构的作用。科氏力在弹射过程中由小变大,是一个近似线性变化的力,由于整个弹射过程只有0.12 s,时间很短,导致钢丝绳很难实现变力的加载;另一方面,由于弹射时间短,钢丝绳拉力加载与导弹弹射的同步性在试验中也很难保证。鉴于以上两种原因,本文Z向加载试验方案:试验系统按顺序由固定墙、螺旋加力装置、水平钢丝绳、竖直加载杠杆和导弹组成,螺旋加力装置一端连着固定墙一端连着水平钢丝绳,水平钢丝绳的另一端连着竖直加载杠杆,钢丝绳和导弹处于加载杠杆旋转轴的同一侧,在水平钢丝绳Z向拉力的作用下竖直加载杠杆对导弹产生Z向挤压力,从而模拟科氏力对导弹的作用。加载方法:在弹射前,对螺旋加力装置按要求进行力的加载,从而通过钢丝绳的水平拉力对加载杠杆产生一个恒定的力矩;导弹发射时,由于导弹在竖直加载杠杆上持续下滑,导致导弹在加载杠杆上的力臂由大变小,加载杠杆对导弹的挤压力由小变大,从而模拟了科氏力的变化。该加载方案克服了科氏力变化加载的困难以及加载和弹射的同步性难题,其模拟精度在工程上也能接受,基本能够验证本文提出的刚度匹配方法是否有效。导弹弹射发射时,利用高速摄影设备测量导弹尾部的横向位移,高速摄影设备的采样频率为1 000 Hz。另外,预先在导弹尾部附近放置比对尺以便于验证试验测量数据的有效性。图9为LAU-142A构型试验用弹射发射装置。

图9 LAU-142A构型弹射发射装置
图10为采用刚度匹配设计前后弹射试验曲线图。从图10可知,从弹射启动到导弹与发射装置分离时刻,弹射机构在越来越大的科氏力的持续作用下,其横向位移持续增大。在机构没有采取刚度匹配设计时,机弹分离时刻导弹尾部横向位移量为28 mm,采取刚度匹配设计后(机构前后链路刚度比约为0.37),机弹分离时刻导弹横向位移量为16.1 mm。因此,弹射发射机构采用刚度匹配设计后能够有效抑制导弹尾部的最大横向位移。
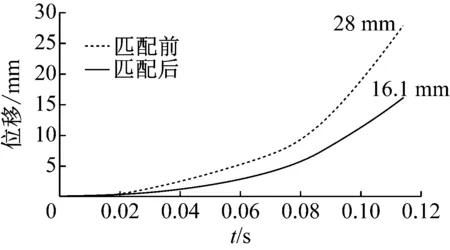
图10 导弹尾部试验横向位移量
需要说明的是,刚度匹配环节虽允许导弹前吊挂相对于其安装座产生较大的Z向位移,但对弹射机构X-Y平面的弹射分离速度和分离姿态影响很小。采用刚度匹配设计后,导弹在挂飞状态时由于锁制机构对弹射机构和导弹的六自由度锁制作用,且机构后挂点对导弹也是六自由度全刚性约束,因此不会出现挂飞时导弹可能存在过大的Z向变形位移的负面效应。另外,片簧材料需要选用疲劳性较好的材料,以满足导弹挂飞时的振动和冲击条件。
5 结 论
(1) 由动力学理论模型可知,当载机滚转发射时,载机的平移速度、滚转速度和弹射机构在伸展过程中的柔性变形之间存在耦合作用。
(2) 载机滚转发射时,导弹弹射分离速度正常;导弹尾部横向位移偏大,影响导弹发射安全性。
(3) 提出的刚度匹配法使弹射发射机构前后链路的刚度设计更为合理,通过仿真和试验表明该方法能够有效减小导弹在弹射发射时的横向位移。
(4) 提出的刚度匹配法,为轻质高速作动的闭链机构提供了一种解决柔性机构姿态问题的新思路,该以柔制柔的方法效果良好且易于工程实施。
