怎样用一个圆形圈住你喜欢的人

刘仔

放眼整个学术界，当属数学家们最能死磕。

为什么“1+1=2”？为什么正五边形无法铺满平面？

为了这些我们用脚趾都能选对的数学题，数学家们打得不可开交，其中争论时间最长的，当属“周长相等，圆的面积最大”这一定理了。数学公主用牛皮圉出个国家

传说，公元前814年，迦太基发生战乱，国家被敌人占领，一下子迦太基变“家太挤”，国王虽下令举国搬迁，但搬到哪里去，依然是个谜。

国家虽然被玩完了，但瞅瞅人家那小金库，金银珠宝不计其数，咱有钱，还怕买不到一块地吗？负责购买土地的迦太基公主更是财大气粗，来到突尼斯，刚一见人家置业顾问，便掏出一张银行卡，说：“这是定金，密码是你生日。”可偏偏突尼斯也是个不差钱的主儿，无论公主出价多少，硬是连个小村庄也不肯卖。眼看谈判就要失败，公主眼珠一转，你不仁我不义，看老娘怎么用数学玩死你。

第二天，公主带着一张牛皮再次登门“突尼斯地产”，说只购买一张牛皮能围起来的面积，突尼斯人一听，一块牛皮能围出多大块地？就赏赐给你了吧。

公主将牛皮剪成小条，沿着海岸线围成了一个半圆，牛皮剪得越细，周长越长，半圆的面积也就越大，而迦太基的人民就在这里建立起了一个国家。

突尼斯人大吃一惊，连忙问公主这是什么操作，“周长相等，圆的面积最大。”公主说，“没事多刷数学题，对脑子有好处。”

怎么证明你是对的？

无论是迦太基公主用牛皮圈出一个国家，还是老百姓们在日常生活中的运用，大家似乎对“周长相等，圆的面积最大”这一定理深信不疑。但如何用数学证明它，谁也想不出方法（估计也没人成天想着要证明）。

直到一位名叫芝诺多罗斯的古希腊数学家，率先提出了他的证明方法，在证明这条定理之前，他先证明了另外两条定理：

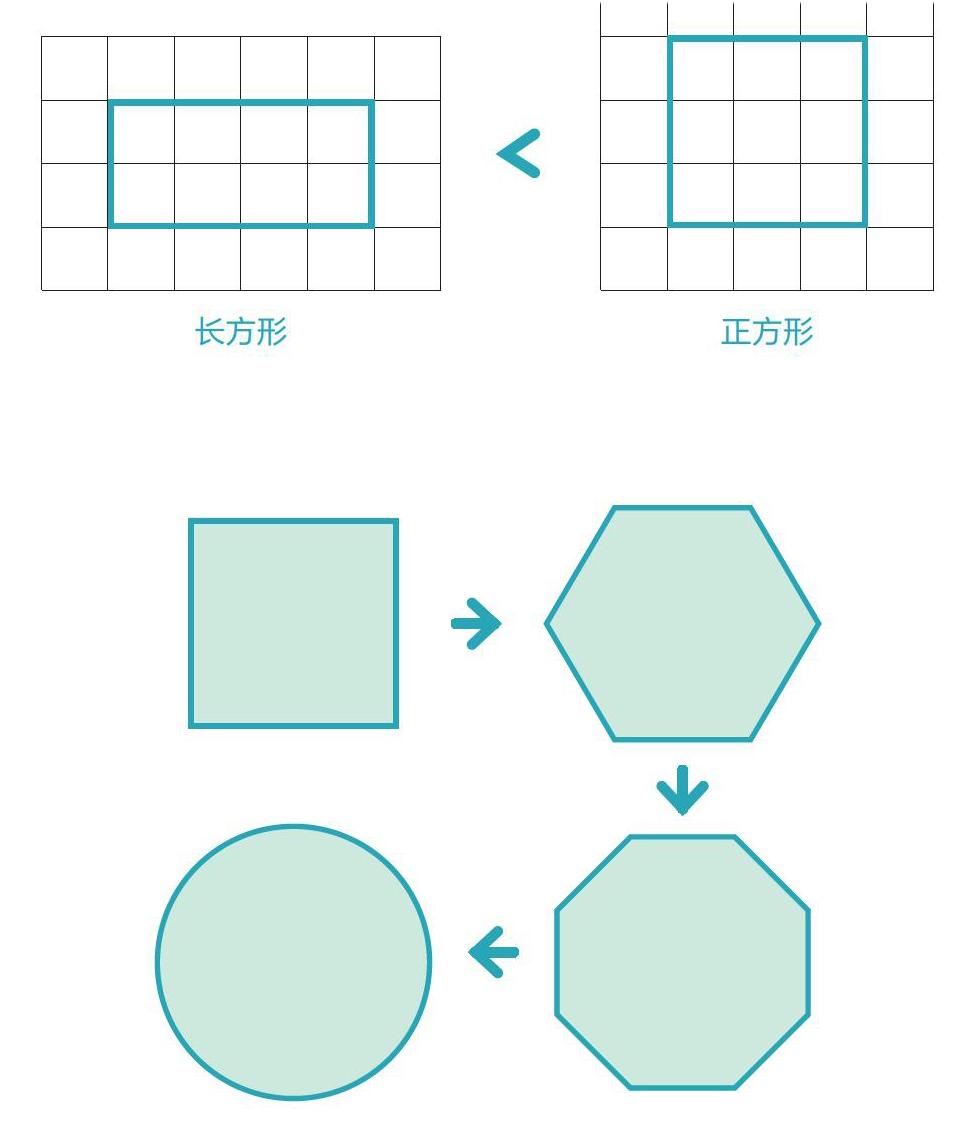
1.等周的多边形中，正多边形面积最大。最直观的例子便是长方形与正方形的对比。

2.同样等周的正多边形中，边数越多面积越大。看看以下图形你就知道了！

在前面两条定理都成立的情况下，“周长相等，圆的面积最大”自然也能成立，这看上去似乎无懈可击，因此在接下来一千多年的时间里，都没人对这种证明方法产生质疑。

时间一晃到了1839年，一位名叫雅可布·施泰纳的德国数学家对证明“圆的面积最大”产生了兴趣。大家都知道，德國人是出了名的严谨，这位数学家也不例外。当他看完芝诺多罗斯的证明过程后，小脑袋瓜立马摇成拨浪鼓，两条定理就想推出正确结论？做梦！再怎么着，也得三条！

面积最大图形特征一：它一定是外凸的！

举个例子，我们将心形内凹的部分向上翻折，变成左边的形状，在周长不变的情况下，面积却大了许多。

面积最大图形特征二：当一条弦平分该图形的周长，那么它的面积也被平分了。

如果一个图形不是对称的，那么它的左右两边总是有大有小，将面积大的一边绕对称轴旋转180°，是不是也能让面积增大呢？

面积最大图形特征三：两段在一条直线上的图形，半圆面积最大

将两段在一条直线上的图形划分成三部分，A、B两部分和三角形c部分，假设A、B固定，要想使三角形周长不变，面积增加，只能将其转换为直角三角形，这是由于直角三角形高线最长。

再结合上述两大特征，我们得出结论“周长相等，圆的面积最大”。

别以为这就结束了，1870年，另一位德国数学家维尔斯特拉斯用变分法再次证明了这一定理，直到20世纪90年代，还有数学家提出自己的证明。

整整两千多年，不同国家不同流派的数学家们为了这条众所皆知的结论，不断提出自己的观点、发表自己的推论。也许在你的认知里，这是一个不用怎么动脑就能说出答案的问题，但在数学家们的世界里，但凡有一丝不合理，都值得用一生去死磕。