薄壁轴承套圈加工方法分析与加强圈尺寸优化
2019-07-23王明杰李凌霄闫继山曲红利段喜川
王明杰,李凌霄,闫继山,曲红利,段喜川
(1.洛阳LYC轴承有限公司,河南 洛阳 471039;2.航空精密轴承国家重点实验室,河南 洛阳 471039)
符号说明
b——磨割宽度,mm
B——轴承宽度,mm
c——加强圈宽度,mm
c′——优化后的加强圈宽度,mm
C——“一拖二”带加强圈加工薄壁轴承的总宽度,mm
d——加强圈内径,mm
D——外圈外径,mm
D2——外圈内径,mm
E——弹性模量,MPa
F——径向载荷力,N
FQ——剪力,N
Ft——圆周力,N
h——加强圈壁厚,mm
h′——优化后的加强圈壁厚,mm
H——轴承壁厚,mm
I——单侧径向截面的惯性矩,mm4
k——套圈刚度,N/mm
l——圆心角θ对应的弧长,mm
M——弯矩,N
N——有效材料体积,mm3
R——惯性半径,mm
W——材料总体积,mm3
δ——任意截面径向位移量,mm
Δ——套圈总形变量,mm
η——材料利用率
θ——圆心角,rad
薄壁轴承具有质量轻,占空间小,惯性矩小等优点,广泛用于工业机器人、航空飞行器、航天卫星、医疗等高端产品领域,且市场规模越来越大。但因截面积较小,使其径向壁厚很小,刚性很低,极易产生较大的径向变形,其套圈在车削加工、热处理、磨削加工等诸多工序都存在加工困难。
1 薄壁轴承加工难点
1.1 车削加工
车削加工主要使用动力卡盘等定心夹具对工件进行装夹,夹具的夹紧力会引起套圈三棱变形等问题[1],这将造成薄壁套圈车削加工后单一径向平面直径变动量超差。
另外,由于刀具对工件的切削力作用,工件受力变形,导致数控车床需要反复调节让刀补偿才能达到工艺要求。但由于工件前工序加工状态存在差异,依然出现车削加工一致性不好,部分工件出现尺寸超差等问题。
1.2 热处理
在热处理淬火工艺中,套圈内部组织产生相变,主要由奥氏体转变为马氏体,密度变小,体积膨胀,产生组织应力。另外,套圈从高温(薄壁产品一般为830~845 ℃)的膨胀状态迅速淬火冷却,还产生了热应力。当上述2种内应力超过材料屈服极限时,材料将发生永久性的塑性变形,即热处理变形[2]。
由于薄壁轴承刚度较低,同样的热处理应力作用下将产生更大的变形[3]。
1.3 磨削加工
磨削时由于电磁无心夹具、支承、砂轮对套圈的复杂作用,薄壁套圈易发生较大变形[4],进给量与实际磨削量之间存在差异,不易控制尺寸,导致薄壁套圈不规则变形,椭圆度等精度超差。此外,由于套圈易变形,相应地降低了磨削力,因而磨削效率较低。
1.4 解决方案
上述加工难点都是由于薄壁轴承套圈刚度较低,变形较大产生的,提高套圈刚度是解决上述问题的有效方法,因此采用带加强圈的方法进行加工。为提高带加强圈加工的材料利用率,选用“一拖二”结构,即1个加强圈带2个套圈同时加工(图1),两侧为2个待加工套圈,中间为加强圈。一般在磨削加工的终磨循环后,使用砂轮把加强圈磨割掉,得到2个成品套圈(端面需修磨,特殊材料可在细磨后终磨前磨割加强圈)。

图1 “一拖二”加强圈结构及尺寸符号示意图Fig.1 Structure and dimension symbol diagram of reinforcing ring with “ two dragged by one”
加强圈的存在提高了待加工件的整体刚度,在车削加工装夹力、磨削加工复合力等作用下变形更小,从而获得更高的加工精度。热处理时由于刚度的提高减小了热处理变形。
2 加强圈尺寸优化
2.1 当前加强圈尺寸存在的问题
在图1所示的尺寸中,两侧用于套圈的尺寸H×B是最终产生成品的有效部分,其余部分均是为了解决生产工艺问题的无效部分。轴承套圈由冲孔→辗扩工艺成形为圆环状的锻件,如图2所示。

图2 套圈锻件示意图Fig.2 Diagram of ring forging
显然,由于锻件形状的限制,造成“一拖二”结构加强圈方式加工的产品材料利用率非常低,生产成本较高。材料利用率为
(1)
以LY-7025薄壁轴承外圈为例,使用带“一拖二”结构的加强圈加工,原工艺尺寸见表1。

表1 LY-7025薄壁轴承外圈原工艺尺寸Tab.1 Original process dimension of outer ring of thin-walled bearing LY-7025
将表中数据代入(1)式计算,可求得原工艺的材料利用率仅为13.446%,且没有考虑车削余量等因素。因此,有必要对带加强圈工艺进行优化,以提高材料利用率。
2.2 加强圈尺寸优化思路
现有工艺参数中:轴承壁厚H、轴承宽度B均为产品设计和工艺需求,不能改动;磨割宽度b是在终磨循环前磨割加强圈时所需要的宽度,由磨具和设备决定,也基本不能改进;可改进的结构参数只有加强圈壁厚h和加强圈宽度c。
因此,加强圈尺寸优化的思路是:在原工艺尺寸的基础上,适当改变加强圈壁厚h和加强圈宽度c,在满足实际生产对刚度要求的同时,最大限度提高材料利用率。
2.3 径向刚度计算
由于薄壁轴承实际加工困难,对加强圈尺寸优化设计的前提是达到原有刚度值,而薄壁零件的变形主要发生于径向,因此首先应对工件径向刚度进行计算研究。
2.3.1 环形体径向力作用下平衡方程
设一圆环如图3所示,该环形体在y轴方向上受一对等大反向力F作用下变形,该环形体在变形后关于x轴、y轴均对称,求圆周方向上任意截面的圆周力Ft、剪力FQ、弯矩M即一次超静定问题。

图3 环形体受径向力示意图Fig.3 Diagram of radial force on a ring
由于2个径向载荷F等大反方向,则x轴上截面A处的剪力FQA必定为零,A,C处圆周力FtA各承受径向载荷的一半
FtA=F/2。
(2)
由受力分析可得A处弯矩MA
(3)
由于图3中4个象限的受力、变形情况完全对称,因此可以只讨论第1象限。以点A受力情况为基础,推论第1象限内任意截面处的受力分析如图4所示,可求得任意截面上的力和力矩为
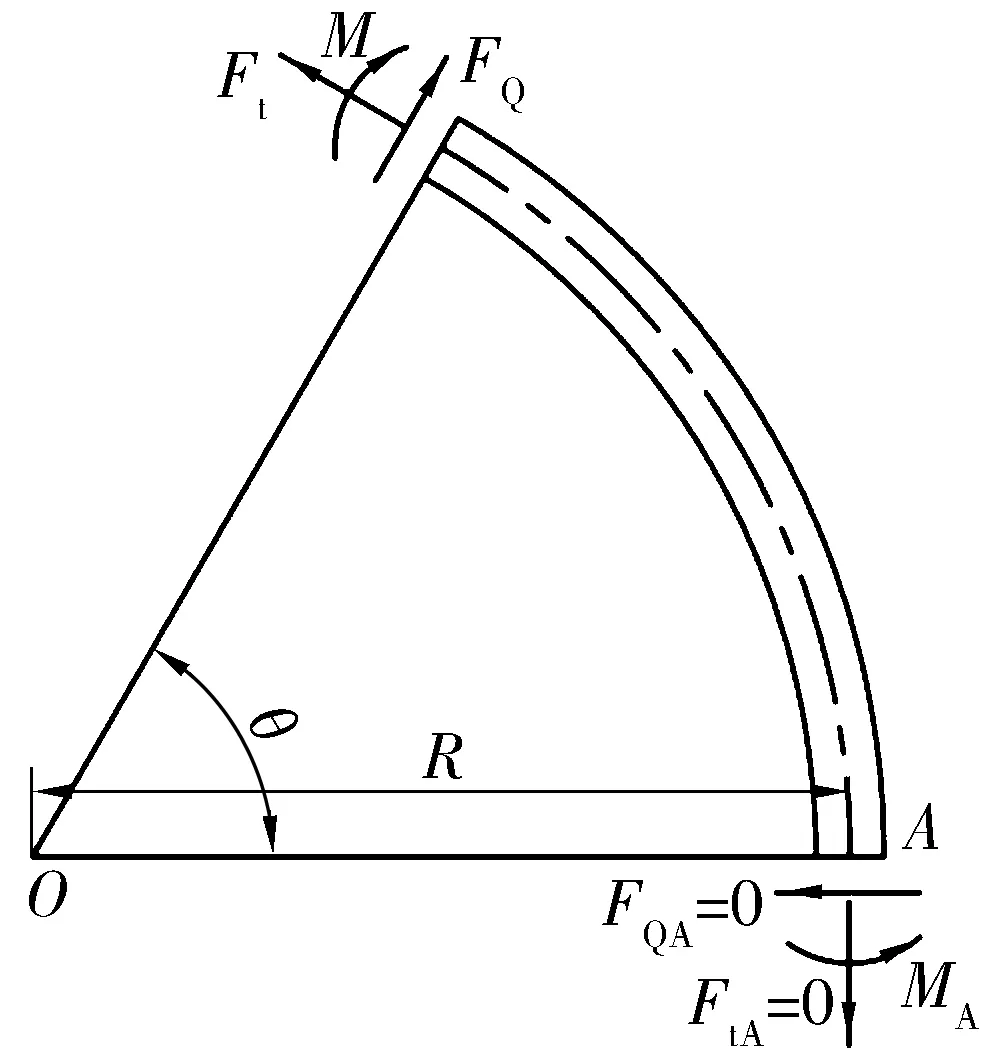
图4 第1象限任意截面受力示意图Fig.4 Diagram of forces on any section of the first quadrant
(4)
由于受力、变形和位移情况相对于x轴对称,所以A,C处在y轴方向上位移为零。设任意截面位置的y轴方向上的位移用δ表示,由材料力学[5]可得变形后的挠曲线微分方程为
(5)
对与x轴夹角为θ的任意截面附近圆弧进行微分,当dθ趋近于无限小时sinθ≈θ,因此有
dl=Rdθ。
(6)
将(4)式中的力矩和(6)式代入(5)式,整理可得圆环径向位移关于角度θ的常微分方程为
(7)
代入2个已知特解:θ=0时,δ=0;θ=π/2及θ=-π/2时,两者δ相等。解(7)式可得
(8)
当θ=π/2时,整个套圈的总径向形变Δ=2δ,此时在2个等大反向力F作用的平衡状态下总形变为
(9)
2.3.2 同刚度下的加强圈尺寸关系
在保证与优化前原有工艺刚度不变的情况下,即刚度不变作为优化计算的约束条件,优化前凭经验确定的加强圈尺寸参数c,h作为初值,讨论加强圈尺寸的关系,对加强圈尺寸进行优化设计。优化后的加强圈宽度和厚度分别用c′和h′表示,并以此类推。则将优化前后刚度相等的条件代入(9)式可得
(10)
图1中重心S到套圈轴线的间距即前文所述惯性半径R,可表示为
(11)
由材料力学[5]可得S到外径面的距离为
(12)
惯性矩为
c(h-a1)3}。
(13)
将优化前、后的(11)~(13)式分别代入(10)式,即可得在同工艺刚度条件下,优化前、后加强圈尺寸参数c,h与c′,h′之间的关系式。
2.4 优化应用
2.4.1 加强圈尺寸优化计算方法
上述推导可以用来优化加强圈尺寸,但具体多大的刚度能够满足工艺需要,因其影响因素非常多,很难定量研究。因此最大材料利用率的计算过程如下:
1)应先给出优化前的加强圈尺寸参数c,h作为优化计算的初值;
2)以优化前、后径向刚度不变作为约束条件,将c,h与其他工艺参数一起代入(10)~(13)式,可得到一个仅有c′,h′的二元方程,整理可得c′关于h′的函数;
3)将结果代入(1)式,可得材料利用率η关于h′的函数,在符合实际范围内求此函数最小值处的h′即为最终优化后的加强圈厚度;
4)将h′的最终结果代入(10)~(13)式,即可得到最终优化后的加强圈宽度c′。
2.4.2 加强圈在外侧时的结论推广
当套圈的内表面精度要求较高时(如内圈内径精度要求远高于内外径),可以采用加强圈位于外侧的加强结构,如图5所示。

图5 加强圈位于外侧的加强结构Fig.5 Reinforcing structure of outer reinforcing ring
此种外侧加强圈的方式能够无干涉地加工内表面,在初磨、细磨循环获得更高的内表面精度。其计算方法与前文所述内侧加强圈的方式基本相同,同理可得
(14)
(15)
同理,根据(10)式和(12)~(15)式可将外侧加强圈的尺寸参数进行优化。
2.4.3 优化后效果
由于给出的结论方程组较为复杂,人工计算求极值较为费力,建议使用计算机程序辅助求解。输入产品参数及初始加强圈尺寸参数c,h,根据文中的计算方法迭代求解即可得优化后的加强圈尺寸参数c′,h′。
薄壁轴承使用文中理论优化加强圈尺寸参数前后对比见表2。

表2 优化前后效果对比Tab.2 Effect comparison before and after optimization
从表中可以看出,在原材料体积相同的情况下,材料利用率提高了1.13%,相应地降低了车削、磨削余量,节约了劳动时间及其他损耗,从多方面降低了成本。
3 试验验证
3.1 径向刚度测量方法与仪器设计
在应用前,为充分证实计算的准确性,通过刚度测量试验验证了刚度计算结论的准确性。设计的试验测量仪器如图6所示。

1—高度表架;2—下支承座;3—待测工件;4—0.2 μm精度数显表;5—加载杠杆;6—转轴;7—加载砝码;8—杠杆支座图6 径向刚度测量仪器示意图Fig.6 Diagram of radial stiffness measuring instrument
理论计算时采用2个等大反向的径向载荷,为了与理论计算情况相一致,测量仪器中使用下支承座作为待测工件的固定端,保证足够的系统刚性。另外,下支承座的工作表面设计为一个大曲率圆弧截面,该设计与待测工件的外圆柱面接触时具有自定心功能,且保证近似于线接触,能够保证测量方式最大限度地与理论计算条件中的径向集中力相吻合。通过杠杆机构在工件外圆柱面上加载,加载可通过在杠杆中间位置加砝码实现,之后通过理论力学可计算实际径向载荷。由于加载杠杆位于待测工件的移动端,因此杠杆系统部分的刚性对测量结果没有影响。最后通过测量仪表对比加载前后的位移,最终计算得到刚度。
3.2 与理论计算的差异
为了便于计算,前文将2个等大反向径向力的方向假设为远离圆心的拉力,而在本试验仪器中,施加的径向载荷为指向圆心的压力。这是本试验与理论计算模型唯一的不同点。对此可通过ANSYS有限元分析的方法证明:等大的一对径向压力产生的位移与等大的一对径向拉力产生的位移绝对值完全相等,不影响刚度计算。有限元分析结果位移云图如图7所示,左侧为拉载荷,右侧为压载荷,载荷均为981.784 N,位移的最大值均为0.457 mm,与理论值误差约为3.604%,说明仿真结果可靠。
3.3 刚度测量结果与对比
对于优化后的工件,使用0.2 μm精度数显表测量其总位移,每组载荷下测量3次取平均值,测量结果见表3。
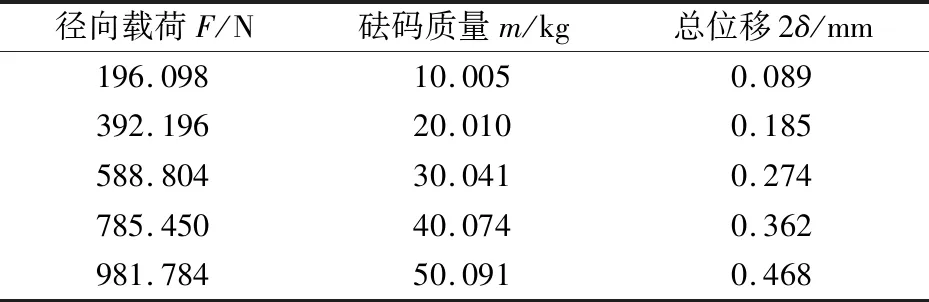
表3 位移测量结果Tab.3 Measuring results of displacement
使用最小二乘法将径向载荷、总位移拟合为线性回归方程,方程斜率即为测量刚度(2.172×106N/m),最终计算刚度为2.108×106N/m,误差为2.947%,属于可接受的正常误差范围,说明计算方法的有效性及准确性。
4 结束语
薄壁轴承套圈各工序加工的难点主要源于工件径向刚度不足,为解决此问题,使用带加强圈加工的工艺方法。同时,针对薄壁轴承带加强圈加工材料利用率非常低的问题,在同等刚度条件下优化了加强圈的宽度和厚度,推导了径向刚度理论计算公式,并通过设计的径向刚度测量仪的测量结果验证了理论计算方法的准确性。
实际加工结果表明,薄壁轴承套圈按照优化后的加强圈尺寸加工,同原有尺寸一样,完全能够满足实际加工过程中各工序对刚度的要求。
