波浪作用下悬浮结构水动力特性分析
2019-07-23金瑞佳耿宝磊张华庆
金瑞佳,刘 宇,耿宝磊,张华庆
(1.交通运输部天津水运工程科学研究所 港口水工建筑技术国家工程实验室 工程泥沙交通行业重点实验室, 天津 300456;2.中国海洋大学 工程学院,青岛 266100;3.太原理工大学 水利科学与工程学院,太原 030024)
水下悬浮隧道(Submerged Floating Tunnel)又名“阿基米德桥”,是一种悬浮在水面下方30 m左右的通道,该结构的空间很大,足以满足道路和铁道等交通方式的要求,悬浮隧道这一概念一经提出,其作为一种跨越河流、湖泊、海洋的新型交通方式便受到全世界范围内研究学者的广泛关注,尤其在挪威、意大利、美国、瑞士、日本等国[1-5]。悬浮隧道通常由浮在水中的管状通道、支撑结构和与两岸相连的构筑物组成,其中支撑结构有三种固定形式,即立柱支撑式,张力腿(缆索或钢管构成)固定式和水面浮箱撑托式。
断面形式被认为是设计悬浮隧道时考虑的最主要因素之一,它必须具备最优化的形状和尺寸,以降低水动力对结构的影响。各国研究人员对悬浮隧道的截面做了不同形式的设计,包括圆形,椭圆形,矩形,多边形等,每一种断面形状受到的水动力荷载及其运动响应存在较大差异,因此在悬浮隧道前期设计中,考虑环境载荷下断面选型是工程设计关键问题。
Mandara等[6]采用静态和动态两种方式,通过改变当前的速度和隧道残余浮力的给定值进行分析,并考虑具有相同运输布局和容量的圆形和椭圆形截面,从水动力的角度研究表明,椭圆截面的运输能力稍好,其水平位移更低,流线型的椭圆截面存在更多有利的水动力特性。Li和Jiang[7]以隧道结构形式为切入点,分析了双车道隧道结构的特点,其研究结合流体计算和结构计算,对比椭圆和矩形隧道结构对压力、流场稳定性的影响,并提出矩形截面有利于加工和运输,椭圆截面有利于流场的稳定性。罗刚等[8-9]通过大涡数值模拟比较分析了不同断面形式、不同来流速度和不同迎流面宽度情况下悬浮隧道周围流场分布和结构所受的作用力,发现耳形断面形式悬浮隧道周围压强较大,结构物稳定性好,升力系数和阻力系数较小,结构受力较小,是最为合理的截面形状,然后依次为圆形、椭圆、六边形和矩形,其研究仅考虑了水流作用的情况,并没有考虑波浪对不同截面形状悬浮隧道的影响。李勤熙等[10]研究了波浪作用下椭圆形截面悬浮隧道管段压强特性试验,分析悬浮隧道结构在不同波高、周期下的迎浪面、背浪面和上下表面的压强变化特性。王广地等[11]进行了水下悬浮隧道管段结构流阻特性分析,对圆形、多边形、曲边形和椭圆四种断面的绕流情况进行了数值模拟,研究表明同种断面的压力分布规律相同且管段曲率是影响绕流场的重要因素。Ding等[12]综合分析了水下悬浮隧道的研究进展并进行展望,针对截面选型提出剖面形式是根据流动水的情况确定,且针对目前研究中提出的相对合理的耳形或椭圆截面形式,需要对某一截面形式的水动力响应规律在大雷诺数的情况下进行实验研究,以进一步验证和比较。Zhang和Lin[13]等研究了沉埋式隧道的断面布置和结构设计,分析了影响截面的因素,并指出截面设计对隧道的安全性和经济性的重要性。Seo[14]等采用经验公式对淹没悬浮隧道的行为进行了研究,并与实验结果进行了对比,通过对经验公式的修正,既保证了计算结果,又提高了计算效率。
此外,在悬浮隧道结构动力特性研究方面,项贻强等学者[15-17]针对动力荷载作用下水下悬浮隧道管体的位移响应进行了研究,分析了锚索刚度、移动荷载大小、移动荷载速度等对隧道管体振动位移的影响。董满生等学者[18-20]研究了地震作用下水中悬浮隧道的动力响应,通过数值分析得出锚索的位移和速度功率谱,进一步分析锚索的动力响应。Liang和Jiang[21]对水下悬浮隧道所受交通荷载的影响因素进行研究并进行仿真模拟分析,但并未考虑结构选型本身会对交通荷载造成的影响。Jin和Kim[22]研究了波浪和移动荷载影响下900 m的悬浮隧道的动力响应,但是其水动力部分采用经验公式进行计算,并未考虑大尺度悬浮隧道对波浪场的影响。
尽管很多学者已经对悬浮隧道进行过大量的研究,但是他们或偏重结构动力特性的研究,或水动力部分仅基于经验公式的研究,或者只考虑水流作用下的影响,而实际情况下有的悬浮隧道的建设地点波浪荷载同样需要考虑。由于悬浮隧道结构尺度较大,其存在会对波浪场产生影响,故采用基于二维势流理论的高阶边界元方法[23]针对圆、椭圆和双圆三种不同隧道截面在海洋中的水动力特性进行分析,为悬浮隧道的截面设计提供参考。
1 基本方法
边界元法以定义在边界上的边界积分方程为控制方程,通过对边界分元插值离散,化为代数方程组求解。它与基于偏微分方程的区域解法相比,由于降低了问题的维数,而显著降低了自由度数,边界的离散也比区域的离散方便得多,可用较简单的单元准确地模拟边界形状,最终得到阶数较低的线性代数方程组,同时由于它利用微分算子的解析的基本解作为边界积分方程的核函数,通常具有较高的精度。

图1 坐标系示意图Fig.1 Schematic diagram of coordinate system
1.1 控制方程边界条件
由于悬浮隧道在通常具有较长的尺寸,当描述波浪与其相互作用的时候,通常可以建立一个二维坐标系Oxz(如图1) 来进行研究。z=0在静水面上,z轴垂直向上为正。水中结构物中心距离静水面高度为h,称之为淹没深度,Ω为所研究的流体区域,SF为自由水面,SB为物体表面,SD为水平海底,SU为上游立面,SL为下游立面。
在二维模型中对于不可压缩流体,满足拉普拉斯方程
(1)

(2)

(3)
(4)
通常将速度势Φ划分为三部分
Φ=ΦI+ΦD+ΦR
(5)
式中:ΦI、ΦD和ΦR分别为入射势、绕射势和辐射势。绕射势是指当浮体固定不动时,入射波浪作用下在浮体表面产生的速度势;辐射势是指在没有入射波浪作用下,浮体自身运动时在浮体表面产生的速度势。其中,辐射势和绕射势均为向外传播的速度势,统称为散射势。
二维模型中每个结构物有三个自由度,假设入射波浪为频率ω的周期谐波,则可以将时间因子e-iωt分离出来,分解的速度势为
(6)
式中:ξj(j=1,2,3)分别为横荡,垂荡,横摇三个运动方向的运动幅值,φj为浮体在三个运动方向上按单位幅值运动产生的三个辐射势。
则自由水面条件变为
(7)
物面条件
(8)
式中:n为物体表面处的单位法向矢量,指出流体方向为正。dj的定义为
(9)
在海底z=-d
(10)
在上游立面(x<0),当立面与物体的距离较远时
(11)
在下游立面(x>0),当立面与物体的距离较远时
(12)
一阶入射势为
(13)
式中:A为入射波幅值;ω为入射波角频率;k为波数。进一步做结构小振幅反响的假设,在二维模型中,幅射势可表达为三个运动模态的分量形式
(14)
相应的绕射势为
ΦD=Re(φ4e-iωt)
(15)
1.2 积分方程
在流域Ω内,在流体域上对一格林函数和任一散射势应用格林定理得到如下积分方程
(16)
式中:x0为源点;x为场点;α为固角系数,我们将相应的边界条件带入积分方程中,并采用高阶边界元的方法对边界进行离散。
1.3 波浪力的计算
本文主要探究波浪在二维模型下对圆,椭圆单个结构和双圆这类双结构的一阶作用力。通常一阶作用力的计算可以通过物面上水动压力的积分得到。波浪力分解为三部分:激励力,附加质量和辐射阻尼。
作用于物体上的一阶波浪激振力为
fj(1)=iωρ∬SB(φ0+φ3)djds
(17)
水动力系数(附加质量和辐射阻尼)
fji=ρω2∬SBφjnids=ω2aij+iωbij
(18)
式中:aij为附加质量;bij为辐射阻尼
2 算例分析
2.1 模型验证
应用上述理论建立的数值模型,通过与其他学者的计算结果进行对比,验证其正确性。付韵韵[24]针对水下淹没圆柱,采用解析的方法进行过计算。
计算水深d=0.4 m,波幅A=0.02 m,圆柱淹没深度h=0.2 m,半径R=0.025 m,图2分别比较了圆柱受到的水平波浪力和垂向波浪力。


2-a 水平方向2-b 垂直方向图2 有限水深情况下淹没圆柱受到波浪力Fig.2 Wave forces on a submerged cylinder at finite water depth
通过上述对比结果,可以明显看出有限水深情况下本文采用的方法计算所得的波浪力与解析解吻合良好,具有较高的计算精度,证明了本数学模型的正确性。
2.2 算例分析
这一部分采用上一节验证的数值模型分别分析了淹没深度对结构物受到水动力特性的影响、截面形状对结构物受到的水动力特性的影响以及结构间特征参数对其水动力特性的影响。
2.2.1 淹没深度对结构物的水动力特性影响
当悬浮隧道位于水下深度不同时,其受到的水动力特性完全不同的,现对一位于水下不同深度的的淹没圆柱进行计算,圆柱尺寸及环境荷载同模型验证算例,淹没深度除了0.20 m之外又增加了0.15 m和0.25 m两个深度,所受波浪力的计算结果如图3所示。


3-a 水平方向3-b 垂直方向图3 不同淹没深度情况下圆形结构受到的波浪力Fig.3 Wave force on circular structures at different submerged depths
由上图可知,水平波浪力和垂向波浪力均随着淹没水深h的增大而减小,在同一深度情况下,波浪力均发生先增大后减小的情况,但是最大值的波数有所不同,随着淹没深度的增加,结构物受到的最大波浪力向低频移动,说明短波对于深水影响很小。接下来对比不同深度淹没圆柱的附加质量和辐射阻尼,附加质量比较结果如图4所示,辐射阻尼的比较结果如图5所示。


4-a 水平方向4-b 垂直方向图4 不同淹没深度情况下圆形结构受到的附加质量Fig.4 Added mass to the circular structure at different submerged depths


5-a 水平方向5-b 垂直方向图5 不同淹没深度情况下圆形结构受到的辐射阻尼Fig.5 Radiation damping of circular structures at different submerged depths
由上图可知,圆形结构受到的附加质量随着波数变化不大,而且受水深影响不大,而辐射阻尼受水深影响较大,当水深变深后,辐射阻尼明显变小。
通过本算例可以发现,结构物淹没深度越大,受到的波浪力越小,但是随之带来的建造难度和施工难度却会增加,因此选择一个恰当的淹没深度对于悬浮隧道的水动力分析十分重要。
2.2.2 截面形状对结构物受到的水动力特性的影响
上一节研究了不同淹没深度对水动力特性的影响,接下来探究相同淹没水深时不同截面形状的结构物受到水动力特性的影响。为比较有目的性,选取淹没面积相同的椭圆与双圆结构进行对比。选取椭圆形截面的原因是用于近似模拟双车道的情况,而选取双圆截面的原因是用于近似模拟两个单车道的情况,计算中,椭圆截面长半轴0.05 m,短半轴0.025 m,双圆截面中每个圆半径R=0.025 m,圆中心距0.1 m。总体水深0.4 m,椭圆和双圆淹没水深选取0.2 m,波幅0.02 m,图6为椭圆和双圆的水平力和垂向力的受力比较。


6-a 水平方向6-b 垂直方向图6 相同淹没深度情况下椭圆和双圆结构受到的波浪力Fig. 6 Wave forces on elliptical and dual-circular structure at the same submerged depth
在水平力方向,总体随着波数增加,先增加后减小,且椭圆截面比双圆截面受力小,原因是双圆之间存在一倍圆直径的距离,波浪会绕过前方迎浪圆柱继续作用在后方圆柱上,从而使双圆所受的水平力高于椭圆截面。在垂直方向,总体和水平力趋势一致,但是双圆截面比椭圆截面受力小,因为双圆之间存在间隔,波浪可以绕过使受力变小,因此椭圆截面所受的垂向力高于双圆截面。接下来对比附加质量和辐射阻尼,结果分别如图7和图8所示。
双圆和椭圆截面在水平方向和垂直方向的附加质量都是随着波数的增加基本保持不变。在水平方向,椭圆截面的附加质量小于双圆截面,垂直方向相反。两种截面形状的辐射阻尼都呈现先增大后减小的趋势,最大值出现的波数基本相同,而且椭圆截面总是大于双圆截面。综上比较发现截面形状不同对淹没结构物受到的波浪激振力和辐射力有较大影响,因此选择一个恰当的截面形状对结构物的水动力分析同样至关重要。
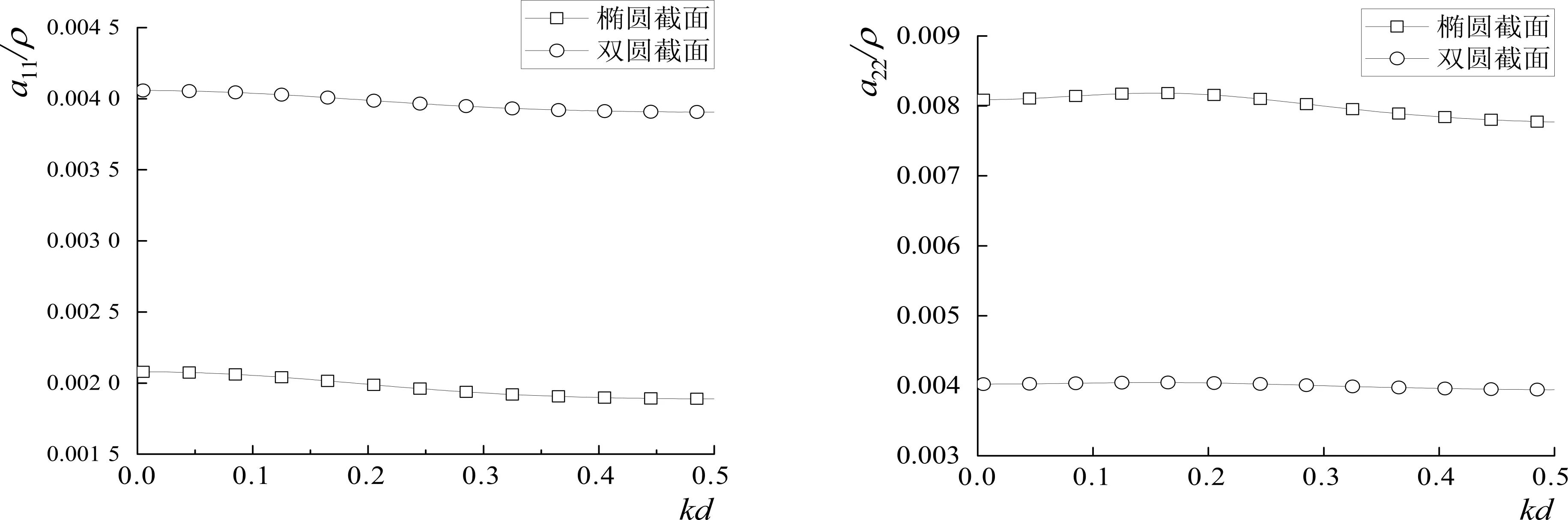

7-a 水平方向7-b 垂直方向图7 相同淹没深度情况下椭圆与双圆结构受到的附加质量Fig.7 Added mass on elliptical and dual-circular structure at the same submerged depth


8-a 水平方向8-b 垂直方向图8 相同淹没深度情况下椭圆与双圆结构受到的辐射阻尼Fig.8 Radiation damping on elliptical and dual-circular structure at the same submerged depth
2.2.3 结构间特征参数对其水动力特性的影响
在悬浮隧道的概念设计中,很多学者提出了双圆型的截面形状,而双圆型的结构间的特征参数对其水动力影响很大。这一节研究不同的中心距对结构的水动力特性的影响。
水深同样为0.4 m,双圆的淹没深度为0.2 m,波浪的入射波幅为0.02 m,选择四组不同中心距(两个圆心的距离)D进行比较。D/(2R)分别为1、1.5、2、2.5。图9是四种不同中心距所受水平力和垂向力的比较:


9-a 水平方向9-b 垂直方向图9 相同淹没深度情况下不同中心距双圆结构受到的波浪力Fig.9 Wave force on the dual-circular structure with different center distances under the same submerged depth
当中心距D/(2R)=1,即两个圆无缝连接时,与其他中心距的波浪力形成较大的对比。水平方向相当于作用在一个刚性物体上,随着中心距的增加,波浪力在间隙间逐渐恢复,连接的双圆所受的水平力就越来越大。而相反的在垂直方向时,当中心距D/(2R)=1,相当于垂向力完全作用在一个无间隙物体上,随着中心距增加,波浪从间隙中穿过,对双圆的波浪作用力就越来越小。附加质量和辐射阻尼的比较结果如图10和图11所示。
对于不同中心距的双圆截面,其受到的辐射力与受到的波浪激振力规律类似,D/(2R)=1.5、2.0、2.5这三种情况下的辐射力相差很小但与D/(2R)=1产生显著差距。不同的中心距的附加质量随波数增加变化趋势基本相同,随着中心距的增大而逐渐变小。辐射阻尼整体随着波数的增加先增大后减小,水平方向随着双圆截面中心距的增加而增加;垂直方向的辐射阻尼随着双圆截面中心距的增加而减少。综上比较发现,双圆中心距对淹没结构物受到的波浪激振力和辐射力有较大影响,因此选择一个恰当的中心距对双圆截面的水动力分析至关重要。

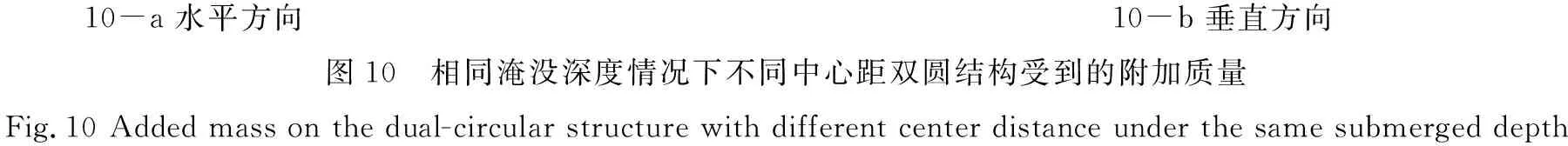
10-a 水平方向10-b 垂直方向图10 相同淹没深度情况下不同中心距双圆结构受到的附加质量Fig.10 Added mass on the dual-circular structure with different center distance under the same submerged depth


11-a 水平方向11-b 垂直方向图11 相同淹没深度情况下不同中心距双圆结构受到的辐射阻尼Fig.11 Radiation damping on the dual-circular structure with different center distance under the same submerged depth
3 结论
本文应用基于势流理论的高阶边界元法对类圆管类结构物在波浪作用下的水动力性能进行分析,得出以下主要结论:
悬浮隧道在不同的淹没水深下所受波浪力各不相同,随着淹没水深的增加而受波浪力和辐射阻尼减少,附加质量几乎不变。所以在设计悬浮隧道的时候要选取适当的淹没水深,既要保证工程的安全性又得考虑适宜的经济成本。比较椭圆和等同面积的双圆截面,椭圆截面受到水平波浪力和附加质量小于双圆截面,而垂向力正好相反;两种截面形状的辐射阻尼椭圆截面总是大于双圆截面,因此选择一个恰当的截面形状对结构物的水动力分析同样至关重要。针对双圆截面形式的悬浮隧道,中心距对双圆截面的水动力特性有较大影响,在水平方向,随着中心距的增加结构受到的波浪力和辐射阻尼也增加,而在垂向方向相反,附加质量则均随着中心距的增加而减小,因此选取最佳的双圆截面中心距是双圆截面形式悬浮隧道的关键。
应用本文数学模型可以精确的计算不同截面形式的悬浮隧道在波浪作用下的水动力系数,为后续的结构动力计算提供准确的输入条件,从而为结构整体的模态分析及动力分析提供数据支持。
