技术创新能改善初创企业的生存吗——一个理论与经验研究

伏玉林，张玉洁（. 华东理工大学 商学院，上海 0037； . 华东理工大学 理学院，上海 0037）

一、问题提出

创新是提高企业核心竞争力、改善企业生存和发展的源动力。近年来，我国政府为鼓励企业创新创业，大力倡导“大众创业、万众创新”，各类市场主体创新创业活力竞相迸发，一大批高科技企业迅速崛起。来自国家统计局数据显示，2017年全国共有29.8万家、占总数39.9%的企业开展了创新活动，其中工业和服务业企业创新活动占比分别达到50.6%和29.3%。创新在一定程度上已成为企业生存和发展的共同选择。但是，创新在给企业带来超额利润的同时，也产生了风险和不确定性，威胁着企业的生存和发展。根据国家统计局的全部国有企业及规模以上非国有工业企业数据库统计，1998-2011年间中国制造业企业平均生存时间约为6.64年，退出率年均17%；有科技创新活动的企业平均生存时间约为6.82年，近50%的创新企业在进入市场的前6年就退出市场，市场中存活10年的创新企业不足10%。市场高退出率是中国转轨时期企业发展面临的突出问题（毛其淋和盛斌，2013），而技术创新通过各种渠道影响着企业生存（Audretsch，1991；Zhang和Mohnen，2013；鲍宗客，2016a）。因此，揭示技术创新影响制造业企业的生存机理并给出中国特色的经验证据是一个重要的研究课题。

本文旨在研究技术创新对初创企业生存的影响机制，并采用2001-2007年我国全部国有企业及规模以上非国有工业企业数据进行实证分析。研究发现，研发强度与企业生存之间遵循规模效应递减的倒U形关系；研发强度和市场集中度对企业生存的影响是互补的，在研发强度相同情况下，高集中度产业的企业存活时间更长；创新和企业生存的关系还受到行业技术水平和产权性质的影响。本文可能的贡献在于：构建了一个熊彼特主义竞争与创新理论模型，将研发投入的规模效应以及市场集中度纳入同一分析框架，丰富了技术创新对企业生存影响的研究；由于样本数据存在删失（censoring）问题，大多数文献采用Cox生存分析模型来解决，相比这种单一方法，本文采用Kaplan-Meier乘积极限、Weibull、Cox及Cloglog模型等多种生存分析方法进行比较，全面深化了这一问题的研究。本研究有助于加深理解技术创新对企业生存的影响，对贯彻落实“大众创业、万众创新”等相关政策具有一定的借鉴意义。

本文剩余部分的结构安排如下：第二部分梳理既有文献；第三部分构造理论模型与研究假说；第四部分说明并解释数据来源、模型设定及变量说明；第五部分报告了实证结果并进行分析；第六部分是结论与启示。

二、文献回顾

大多数研究结果显示，技术创新改善了企业生存。企业通过技术创新，可以提高生产率（Griliches，1979；孙晓华和王昀，2014），迅速占领市场或维持既有市场竞争优势，强化了企业的市场势力（Aghion等，2014），因此创新企业相对于非创新企业有更高的收益，在市场中存活更久（Audretsch，1995；张杰等，2014）。各种创新指标几乎都证实了技术创新与企业生存之间呈显著的正向关系，一些研究把创新倾向作为衡量指标，认为技术创新是维持企业生存的关键，技术创新对企业生存概率有着显著的促进作用（陈阵等，2014；Jung等，2018），并且创新企业较非创新企业有更好的生存前景（张慧和彭璧玉，2017）。采用专利、商标、新产品或新工艺等创新产出指标（Audretsch，1991；Cefis 和Marsili，2005，2006）或者创新效率指标（Zhang和Mohnen，2013），结果都表明技术创新与企业生存之间呈现显著的正向关系。一些文献采用研发投资作为创新投入指标进行实证分析，如Hall（1987）采用美国制造业企业面板数据研究发现，研发强度增加了企业生存的概率；Li 等（2010）研究发现企业的研发投入可以显著降低企业的退出概率；Pérez等（2004）采用西班牙制造业企业数据，证实了有研发投资的企业在退出风险上要比没有研发投资的企业大约低57%。

然而，另一些研究显示技术创新与企业生存之间呈不显著、负相关甚至复杂关系。由于研发投资有可能增加企业风险，或构成市场进入退出的随机生产率冲击（Jovanovic，1982；Hopenhayn，1992；Ericson和 Pakes，1995），特别是当企业接近技术前沿时，研发项目的生产率存在规模报酬递减趋势（Kortum，1993）。此外，高集中度行业中的企业大研发项目的市场不确定性通常更高，更可能对企业生存形成冲击（Gilbert，2006；Czarnitzki和Toole，2013）。如Audretsch（1995）在控制企业年龄和规模等特征后发现，小企业的技术创新对生存率没有影响；Wilbon（2002）对美国高技术企业的研究发现，企业生存与研发支出二者之间存在负向关系。大量研究表明不同创新衡量标准对企业生存的影响也存在着差异。如Giovannetti等（2011）发现产品创新和过程创新对企业生存没有影响；Buddelmeyer等（2010）研究表明，以专利申请作为高风险创新的衡量标准，创新导致了企业较低的生存率，采用商标权作为低风险创新的衡量标准，创新导致较高的生存率；鲍宗客（2016b）研究发现，研发强度对企业生存风险的影响呈非平稳状态，并非创新强度越强对企业生存风险的抑制作用就越明显。此外，不同行业的创新与企业生存的关系也存在差异。如陈阵和王雪（2014）研究发现创新与企业生存关系在纺织行业不显著，在石油、非金属行业显著为正。Børing（2015）研究表明，创新对企业生存的影响在能源、材料等产业不显著，但在基础产业和特殊技术产业显著为正。Mahmood（2000）使用对数逻辑生存风险模型，将美国初创企业按行业和技术水平划分为17个样本，包括8个低技术产业、6个中技术产业和3个高技术产业，研究发现有11个产业的创新与企业生存关系不显著，有4个是正向关系，2个是负向关系。综上所述，有关创新与企业生存之间的研究结论目前仍呈现多样性关系。

引起研究结论多样性的可能原因在于：一是选取样本、选择变量或估计方法存在差异，但是这些差异并非影响创新与企业生存关系多样性的主要原因（Ugur等，2016）。二是计量模型设定存在一定的偏误。就模型设定而言，一方面创新风险随研发强度增加而增大（Czarnitzki和Toole，2013），且受到所处行业创新水平的影响（Aghion等，2014），偏误可能是由于缺乏对创新规模效应的控制；另一方面市场集中度不同会导致创新投入或产出的不同（Gilbert，2006），偏误也可能是由于缺乏对研发强度和市场集中度交互作用的控制。基于此，我们认为有必要控制研发强度的规模效应以及研发强度与市场集中度的交互作用，为此将研发强度的规模效应以及市场集中度的影响纳入分析框架，并采用不同方法进行估计。

三、理论模型与研究假说

借鉴Aghion等（2014）分析框架，假设企业为多个生产单元或产品创新线的集合，通过一定数量的研发人员和现有的研发生产线进行创新，并以成功的创新来扩展其产品空间。创新的投入产出满足如下恒常规模报酬的Cobb-Douglas生产函数：

其中，Zi表示创新产出，Li表示研发人员数量，ζ表示规模参数，ki表示研发生产线累积的资本存量，1/η表示创新产出对研发人员的弹性，且η＞1。当企业创新成功时，研发生产线增加到k+1。

根据上述创新生产函数，得到企业创新的总成本为：C(zi,k)=ζωkzηi。其中，ω表示工资率，定义zi≡Zi/k为企业的创新强度。则每条生产线的成本为：C(zi)=ζωzηi。显然，总成本和平均成本是工资率和创新强度的增函数。进一步，定义企业的价值方程为：Vt(k)=kYtv。其中，Vt(k)表示企业t时期的市场价值，Yt表示该时期的最终品产出。每条创新线的平均价值为：v=Vt(k)/kYt，它内生决定于企业和行业的特征：

其中，π为每条创新线的利润，πA为扣除创新成本后的利润，ρ为贴现率，x为行业创造性破坏的比率。企业通过选择创新强度zi实现平均价值v的最大化。从式（2）可以看出，创新强度zi对企业价值v的影响是非线性的。企业的市场价值近似等于Vt(k)，假定企业市场价值为零时退出市场，而企业在位时市场价值的变化遵循维纳过程（McDonald和Siegel，1985），由此得到企业的价值方程是一个关于时间的对数正态分布函数：

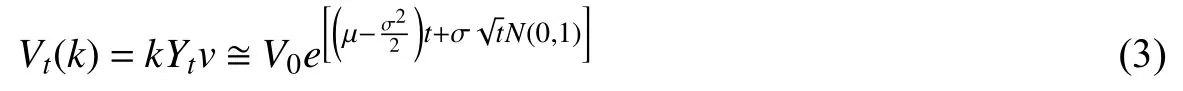
其中，V0表示企业的初始价值，µ和σ分别表示漂移和波动率参数。对式（3）取对数及数学期望，得到如下企业生存时间的期望值：

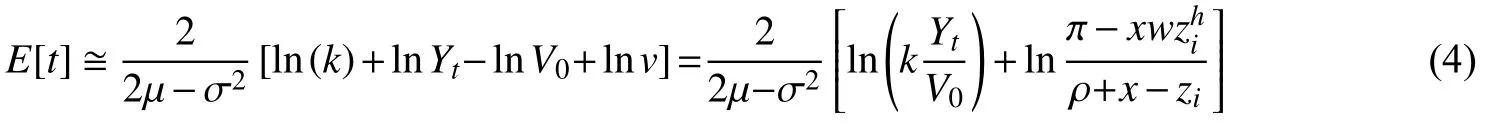
从式（4）可以看出，研发强度zi对E[t]影响是非线性的。式（4）的一阶最优条件为：

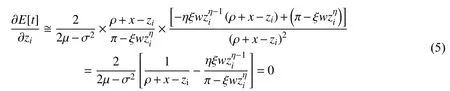
由σ＜2µ可知：2µ-2σ2＞0，因此，ρ+1x-zi=π-ξwizηi，即v=ρ+x-zii=ηξwzηi-1。可以看出，当企业平均价值等于研发强度的边际成本时，企业生存时间的极值可表示为研发强度的函数。

为了研究E[t]与zi之间的非线性关系，式（4）关于zi的二阶偏导为：

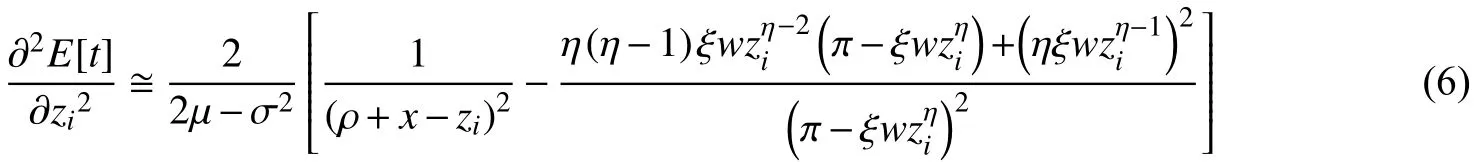
由于π-ξwzηi=πA，v=ηξwzηi-1，得到：

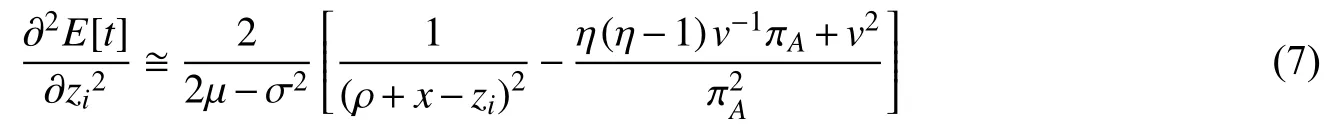
为判断式（7）的符号，对中括号部分乘以π2A并化简得到：

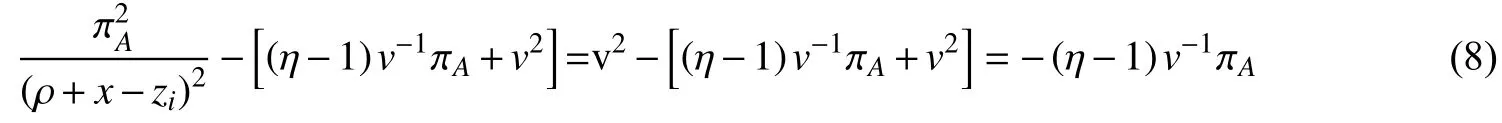
由1/η＜1可知：(η-1)v-1πA＞0，因此式（8）小于0，即生存时间E[t]关于zi的二阶偏导数为负。因此，研发强度与企业生存之间呈倒U形关系。基于以上分析，本文提出第一个待检验假设：

假设1：研发强度与企业生存时间之间存在规模效应递减的倒U形关系。即研发强度存在一个最优水平，在达到最优水平之前，生存时间随研发强度提高而增加，达到最优水平之后，生存时间随研发强度提高而减少。

生存时间E[t]关于研发强度zi和总利润π的混合偏导数为：

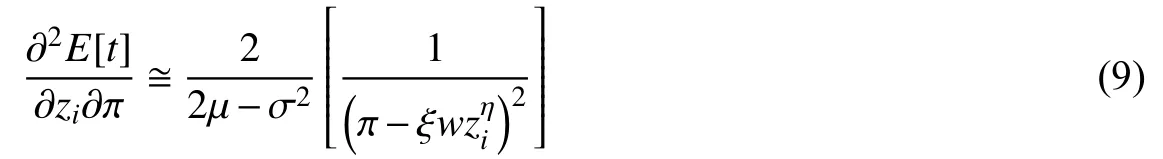
根据上文，可以判定式（9）为正。这表明企业生存时间随利润的增加而增加，即研发强度与利润是互补的。理论和经验研究均表明，不同产业间的企业利润与市场集中度呈正相关关系（Bain，1951；Berger，1995；Slade，2004），参考Ugur等（2016），我们以市场集中度作为利润的代理变量。基于以上分析，本文提出第二个待检验假设：

假设2：研发强度和市场集中度对企业生存时间的影响是互补的，高集中度产业的企业生存时间更长。

四、数据、模型及变量

（一）样本选取与数据来源

本文采用2001-2007年我国全部国有企业及规模以上非国有工业企业数据库数据进行计量研究，该数据库是基于国家统计局进行的500万元以上规模工业企业和国有企业统计报表统计整理得到，包含企业代码、行业代码、企业注册类型、联系方式和地理位置等基本信息以及资产、负债、利润、中间投入和现金流等主要的财务指标。定义企业生存时间为企业从注册成立到退出所持续的时间。如果企业在样本期内某年份退出市场，那么将此事件定义为“失败（failure）”，若失败事件发生，则failure取值为1，否则为0。考虑久期数据（Duration Data）的特征，由于观测不到2001年前在位企业是否发生过失败事件，这会引起统计的生存时间是有偏的，从而导致左删失（left censoring）问题，因此我们选取2001-2007年间初创企业数据来解决此问题。同样，由于无法观测到样本期最后一年仍存活的企业之后是否退出，从而导致右删失（right censoring）问题，因此我们选取生存风险模型来解决此问题，在失败事件取值中，将截尾数据即右删失的样本数据取值为0。此外，为确保数据的可靠性，本文首先删除样本中存在的异常值以及统计中错误记录和不符合财务会计原则的样本（李玉红等，2008）：第一，工业增加值或中间投入大于工业总产值；第二，总资产为负值；第三，固定资产原值小于固定资产净值；第四，各项投入为负值。其次，删除利润总额与销售收入之比、研究开发费与总资产之比大于1等明显不符合逻辑的样本。最终得到的企业数量为201 494，样本观测值数为462 050。

（二）企业生存时间统计分析

表1报告了样本期内初创企业的生存时间统计。（1）所有企业的平均生存时间比较短，仅为4.15年，7.90%的企业在进入市场当年即退出，存活时间少于5年的企业数量占到55.19%，存活时间满7年的仅占12.28%，远低于发达国家的平均水平。从比例上来看，大多数企业在进入市场后的第3-5年退出的概率比较高。（2）按是否有研发投入把所有企业分为创新和非创新两类，创新企业平均生存时间要高于非创新企业。此外，有创新活动的新建企业在第一年内退出概率为5.70%，低于非创新企业的8.10%；生存时间满7年的创新企业占比为16.04%，高于非创新企业的11.93%。这表明对于初创企业而言，创新活动确实提高了企业的生存时间。

表 1 样本期企业生存时间分布

为深入研究企业创新与其生存的关系，本文从技术水平和产权性质两个角度展开讨论。参考既有文献划分方法（伏玉林和苏畅，2013），以行业研发销售比高于或低于全部制造业均值作为划分行业技术水平的现实分类标准，将两位码制造业划分为高技术行业和非高技术行业。按照企业注册实收资本占总实收资本比重，将企业产权性质区分为国有、集体、独立法人、私营、外商投资、港澳台6种产权类型。

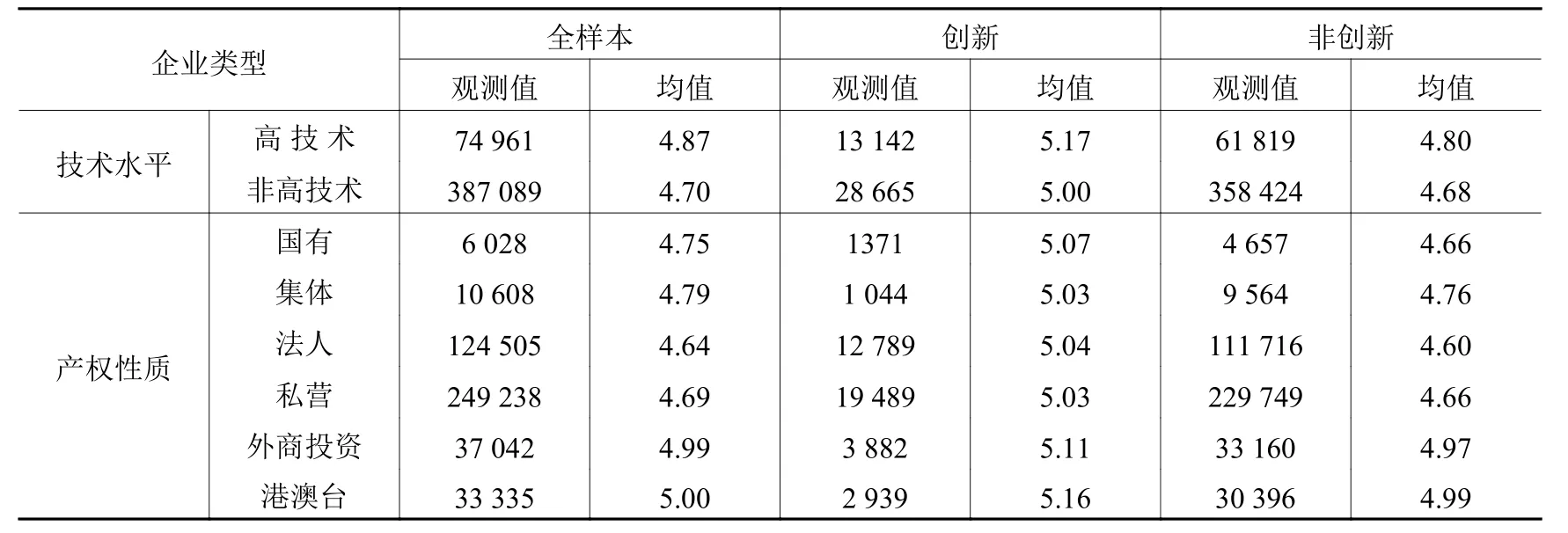
表 2 不同类型企业生存时间描述性统计

表2报告了不同类型企业的平均生存时间。总体上看，创新企业平均生存时间要高于非创新企业；高技术行业的企业平均生存时间为5.17年，高于非高技术行业的企业平均生存时间（4.80年）；外商和港澳台企业的平均生存时间高于其他所有制企业。

（三）企业生存风险估计

在久期数据的生存分析中，通常采用生存函数（生存率）或风险函数（风险率）来描述生存时间的分布特征（Ejermo和Xiao，2014；Prentice和Zhao，2016）。这些方法既不需要对数据的概率分布作先验假设，也不需要估计参数，并且可以显示生存时间的分布规律。基于此，我们选取生存分析常用的乘积极限法（Product-limit）（Kaplan和Meier，1958）来估计企业的生存分布特征。乘积极限法又称Kaplan-Meier法，其估计量为：

其中，t 为生存时间，j为 时期， Nj表 示面临风险的企业数， Dj表 示退出的企业数。根据企业生存率及其标准误绘制生存曲线，表示企业在全部观测期内的生存状况。其中，图1和图2分别反映了企业的生存率和退出风险率，横坐标均为观测期内企业生存时间。

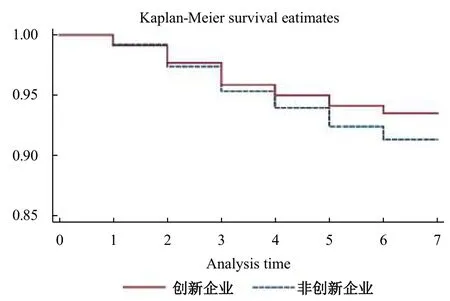
图 1 Kaplan-Meier生存曲线

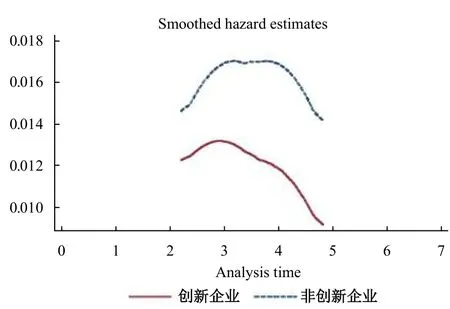
图 2 风险函数曲线

图1 显示：（1）创新企业的生存概率高于非创新企业；（2）创新企业和非创新企业的生存概率均随着生存时间增加而降低，但非创新企业的生存概率下降幅度更大；（3）创新企业和非创新企业生存概率的差值随生存时间的增加而越来越大，这意味着随着时间的增加，创新企业存活概率越来越大于非创新企业。图2显示：（1）两类企业的风险函数曲线都大致呈倒U形，但非创新企业退出风险高于创新企业，与假设1相符；（2）两类企业的退出风险率在第2-5年时比较高，在退出风险率递增阶段，相对于创新企业，非创新企业退出风险率增加得更快，两者差值逐渐增大。因此，非创新企业面临更高的退出风险，而创新企业有更强的抵御风险能力。

（四）模型设定与变量说明

生存风险模型较好地解决了久期数据的右删失问题，常用的生存分布包括指数分布、Weibull分布、Log-normal分布、Gamma分布和Gompertz分布等，这类参数方法的主要优点是通过最大似然法很容易估计参数向量。接下来，我们采用参数回归法，建立Weibull风险模型（Howell，2015；Dzhumashev等，2016），研究创新对企业生存时间的影响，同时引入Cox比例风险模型进行比较。

t时期企业在影响因素x条件下的生存风险函数为：

其中，λ0(t)表示基准风险，x为协变量，β为风险估计参数。对式（11）两边取对数，且令基准风险为λ0(t)=ptp-1eβ0，得到Weibull生存模型的对数形式：

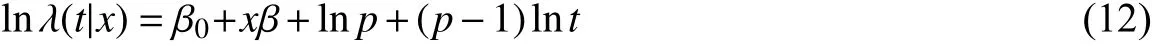
其中，p＞0,γ=eβ0+xβ＞0。如果p＞1，则风险函数λ(t)单调递增，即企业生存时间越长，其退出的概率越高；反之，如果p＜1，则风险函数λ(t)单调递减，即企业生存时间越长，其退出的概率越低。式（12）将非线性回归模型转化为线性回归模型，可以通过最大似然估计得到协变量的β系数。基于式（12），我们设定如下计量模型：

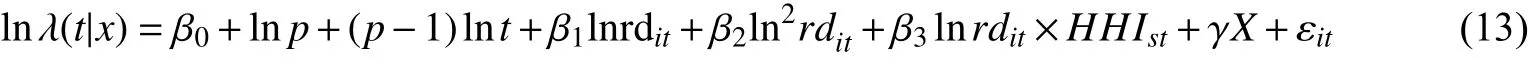
变量说明如下：（1）被解释变量lnλ(t|x)表示企业的生存风险率。（2）解释变量：一是研发强度（lnrd）；二是研发强度和市场集中度交互项（lnrd×HHI），用以检验市场集中度对研发强度与企业生存关系的影响，我们对该交互项进行去中心化处理。为了研究创新与企业生存的非线性关系，引入研发强度平方项（ln2rd）。（3）X为一组控制变量，包括市场集中度（HHI）及其平方项（HHI2）、企业规模（lnsize）及其平方项（ln2size）、企业年龄（lnage）及其平方项（ln2age）、全要素生产率对数值（lnTFP）、销售利润率（profit）、资本密度（lncapital）、人力资本（resource）、广告投入（advert）、出口强度（export）、资产负债率（debt）、所有制结构（ownership）、行业虚拟变量（indus）、年份虚拟变量（year）、省份虚拟变量（prov）。εit为 扰动项，下标 s代表产业，i代表企业，t代表时期。企业规模（lnsize）包括三种测度方式：销售收入（lnsale）、职工人数（lnemploy）和资产总额（lnasset），主要变量定义、测度及统计特征见表3。

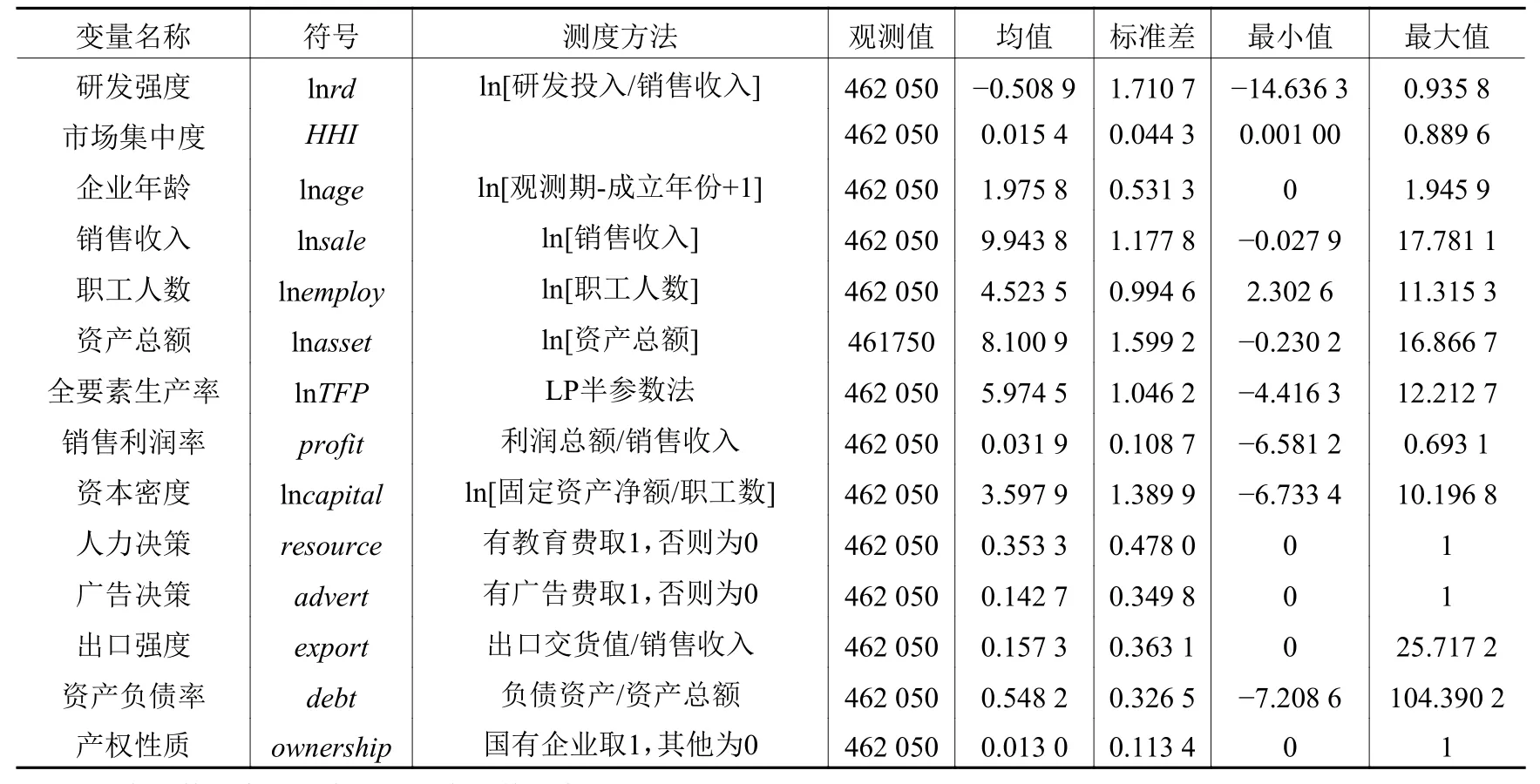
表 3 主要变量描述性统计

五、实证结果与分析

（一）基准回归

表4报告了Weibull生存分析模型的检验结果。模型（1）的解释变量仅有研发强度（lnrd），模型（2）引入了研发强度的平方项（ln2rd），模型（3）引入了研发强度和市场集中度的交互项（lnrd×HHI），模型（4）采用的是Cox生存分析模型以便于比较。

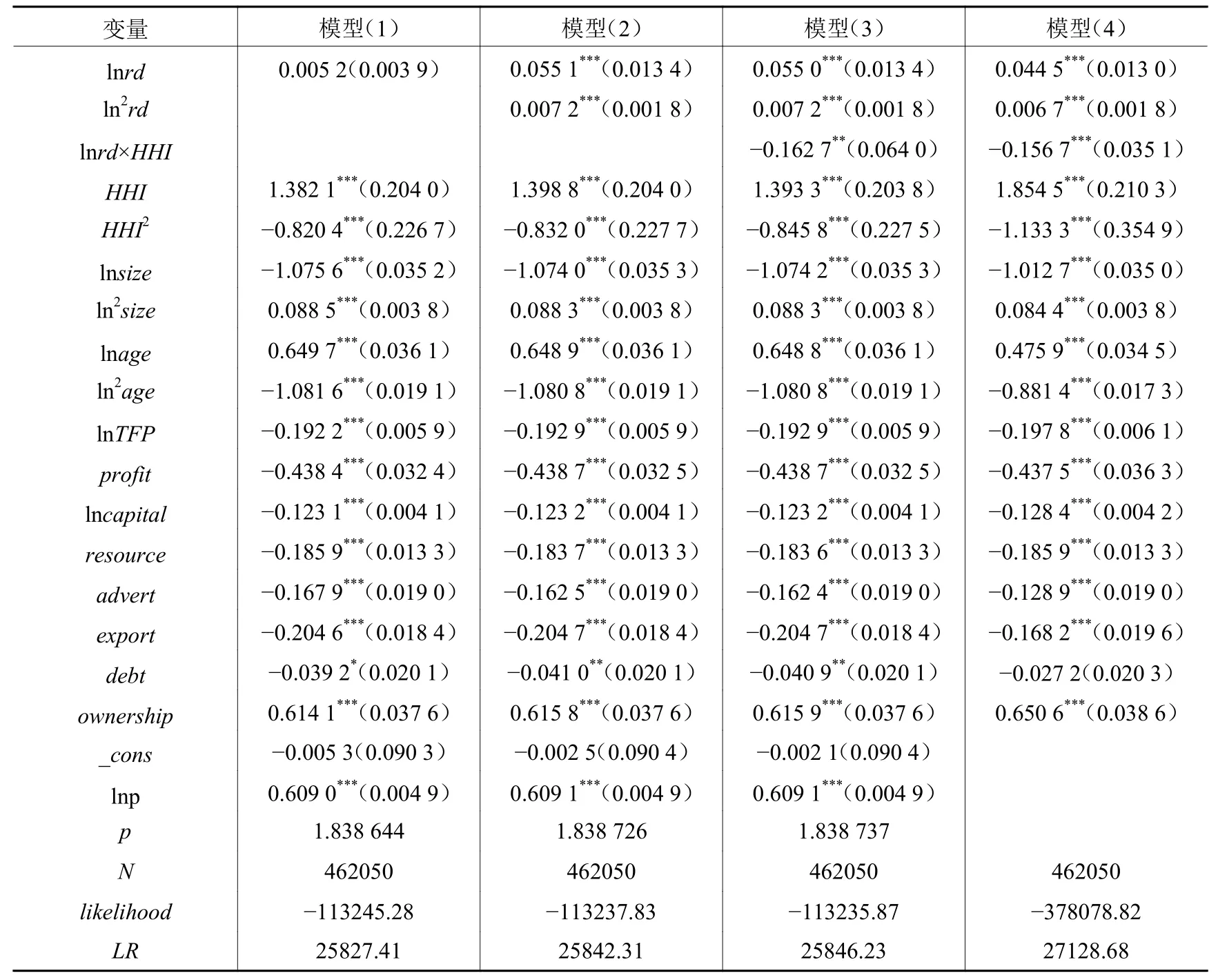
表 4 Weibull模型检验结果

模型（1）中研发强度（lnrd）的系数为正但不显著，表明企业研发强度与生存风险率不存在显著线性关系，证实了研发强度与企业生存的非线性关系，因此有必要控制研发强度的规模效应。模型（2）显示，研发强度（lnrd）及其平方项（ln2rd）的系数都显著为正，表明研发强度与企业生存风险率呈U形关系，即研发强度和企业生存时间之间遵循规模效应递减的倒U形关系，假设1得到验证。模型（3）中lnrd×HHI的系数显著为负，表明研发强度和市场集中度对企业生存的影响是互补的，高集中度产业中的企业存活时间更长，假设2得到验证。模型（4）为Cox回归结果，与Weibull回归结果一致。

控制变量的回归结果显示：（1）市场集中度HHI与企业生存概率之间存在显著的U形关系。寇宗来和高琼（2013）的研究也表明两者之间存在非线性关系。（2）以职工人数（lnemploy）表示的企业规模（lnsize）与企业生存概率呈倒U形关系。小规模企业的风险承受能力较低，随着企业规模的不断扩大，生产水平、企业竞争力和市场占有率不断提高，风险承受能力也随之增强。但是，当企业规模超过一定水平时，企业的技术进步呈现边际递减趋势，盈利水平有可能低于成本消耗，这时企业将面临较高的市场退出风险（王淼薇和郝前进，2012）。（3）企业年龄与企业生存呈倒U形关系。（4）全要素生产率（lnTFP）对企业的生存概率有着正向影响。企业可以通过生产率的提高弥补其高昂的劳动成本，从而提高企业利润率，增强企业的存活能力。（5）销售利润率（profit）的系数为负，说明企业的利润率与退出风险率呈负相关关系，企业利润率越高，竞争力越强，从而降低了企业的退出风险，企业通过持续的利润积累提高企业的生存概率（鲍宗客，2016a）。（6）资本密度（lncapital）、人力资本（resource）、广告投入（advert）和出口强度（export）对企业的生存概率具有促进作用。不同行业的规模、竞争强度以及资本密度是不同的，导致不同行业内的企业生存状况也存在差异；企业的人力资本支出与广告投入均会提高企业的创新能力，进而提升企业的生存概率；出口企业面临激烈的国际竞争，创新意识强于非出口企业，因此生存概率更大（于娇等，2015）。（7）企业资产负债率（debt）是反映企业偿债能力的综合性指标，企业负债经营有利于企业抓住市场机会，带来丰厚的利润，从而有利于企业生存。（8）所有制（ownership）的系数为正，国有企业较非国有企业有更高的生存风险率，说明国有企业的创新活动不利于企业生存。

（二）不同技术水平的回归结果

以研发强度作为划分高技术行业和非高技术行业的现实分类标准（伏玉林和苏畅，2013），将两位码制造业分为高技术和非高技术两类。其中，样本期内高技术行业包括医药制造业、专用设备制造业、交通运输设备制造业、电气机械及器材制造业、通信设备计算机及其他电子设备制造业、仪器仪表及文化办公用机械制造业。不同技术水平的回归结果如表5所示。

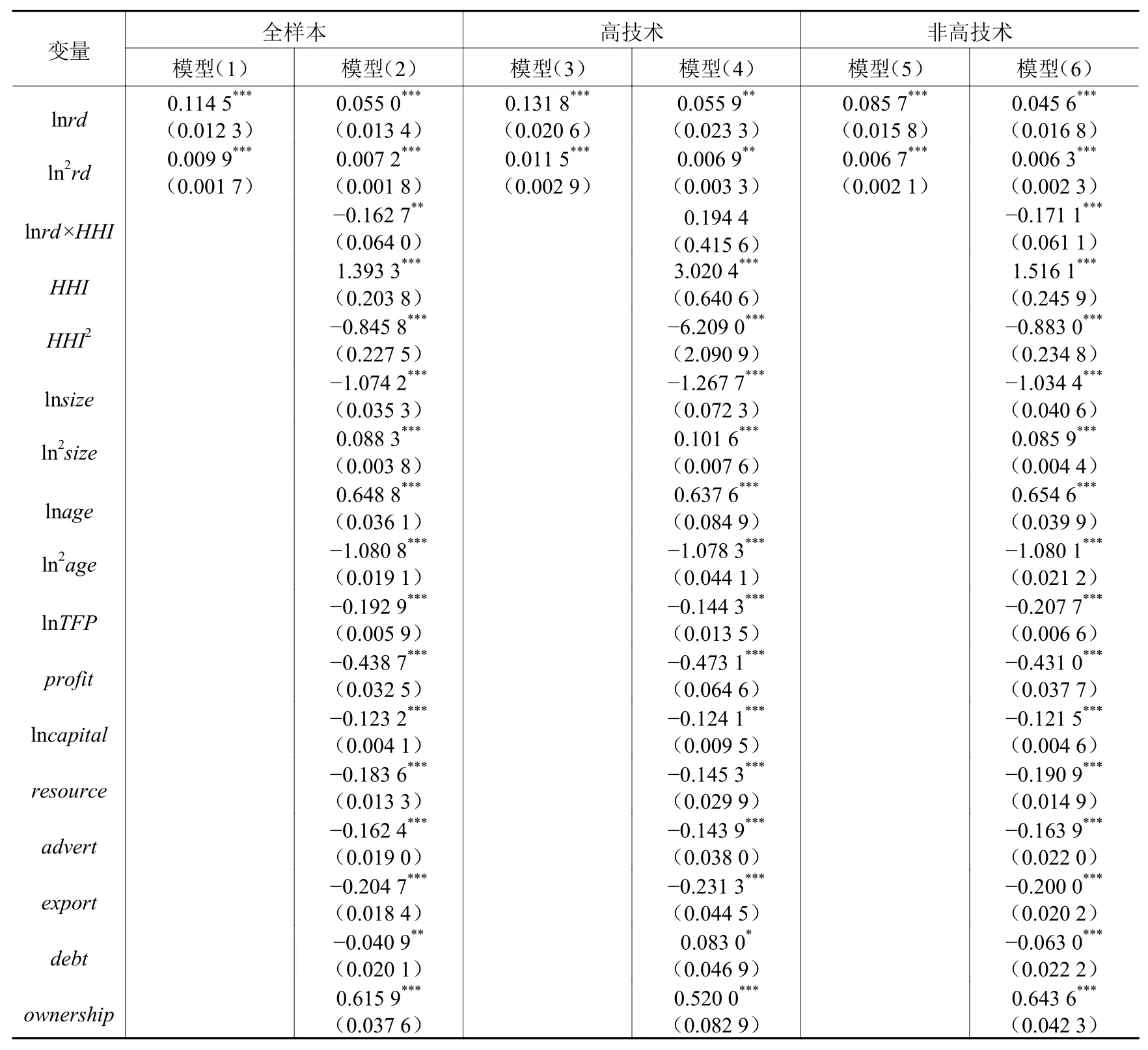
表 5 不同技术水平的回归结果

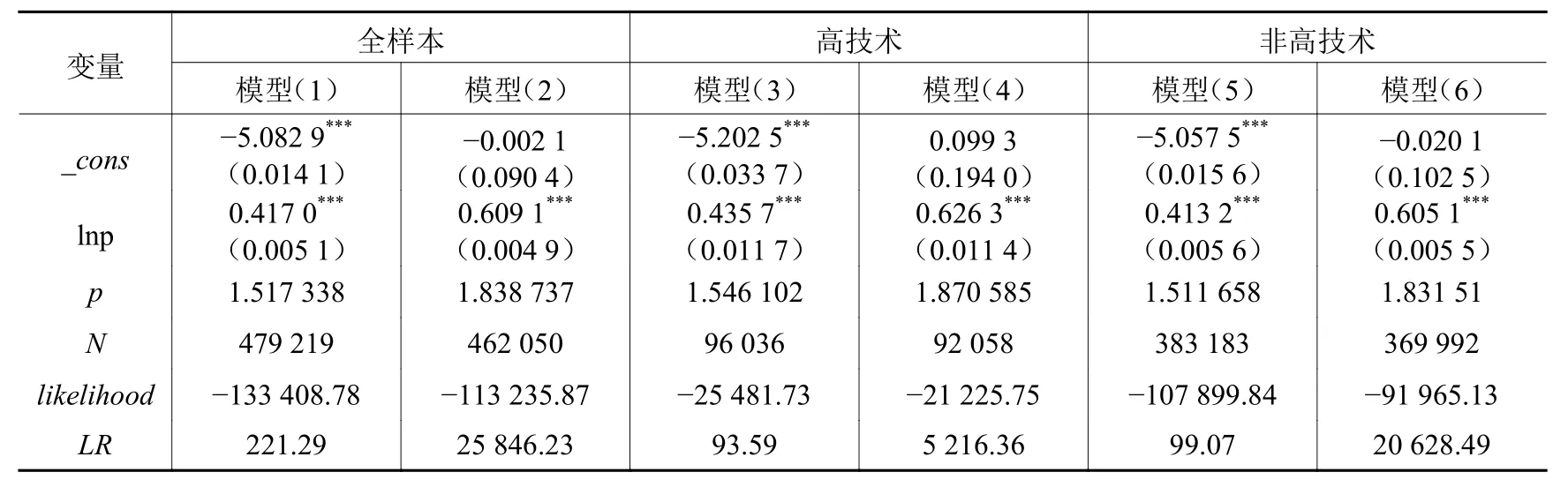
续表 5 不同技术水平的回归结果

从表5中可以看出，无论是高技术行业还是非高技术行业，研发强度和企业生存概率之间的关系均呈倒U形关系，但是二者之间存在显著差异。模型（1）、（3）、（5）报告了无控制变量下，全样本、高技术产业和非高技术产业的研发强度对企业生存概率的影响，通过计算这三个模型的研发强度最优水平来确定最长生存时间。高技术行业的企业研发强度最优水平高于非高技术行业企业，高技术行业的企业最长生存时间约为5.58年，高于非高技术行业的企业最大生存时间5.33年。图3显示了高技术行业和非高技术行业的企业研发强度最优水平及生存时间最大值。结果表明：高研发强度更有利于高技术行业的企业生存，这是因为高技术行业具有更好的技术机会和创新独占性，更容易获取高额创新利润，从而降低了生存风险率。但从总体回归结果来看，高技术行业和非高技术行业企业的研发投入均能改善企业生存。

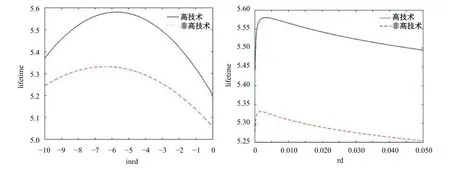
图 3 不同技术水平下研发强度与企业生存时间曲线图（Matlab制图）

（三）不同产权性质的回归结果

根据表2的统计分析可知，同样是创新企业，由于产权性质不同，其存续时间明显不同。不同产权性质的企业由于技术条件、融资约束、退出壁垒以及生产率等差异，在开展技术创新时会面临不同的风险或不确定性，从而对企业生存的影响可能存在明显的差异。如采用中关村海淀园全样本数据研究发现，国有高技术企业的生存概率高于非国有高技术企业（马玉琪等，2018）。因此，本文接下来划分产权性质实证分析创新对企业生存的影响。

表6报告了国有企业、民营企业和外资企业的技术创新对企业生存的回归结果。可以看出，国有企业和私营企业的研发强度与企业生存均呈倒U形关系，外商投资企业的研发强度与企业生存关系不显著。通过计算模型（1）、（3）和（5）研发强度最优水平来确定企业的最长生存时间，我们发现最优研发强度从大到小排序依次是私营企业、国有企业、外资企业，而最长生存时间从大到小排序依次是外资企业、私营企业、国有企业。

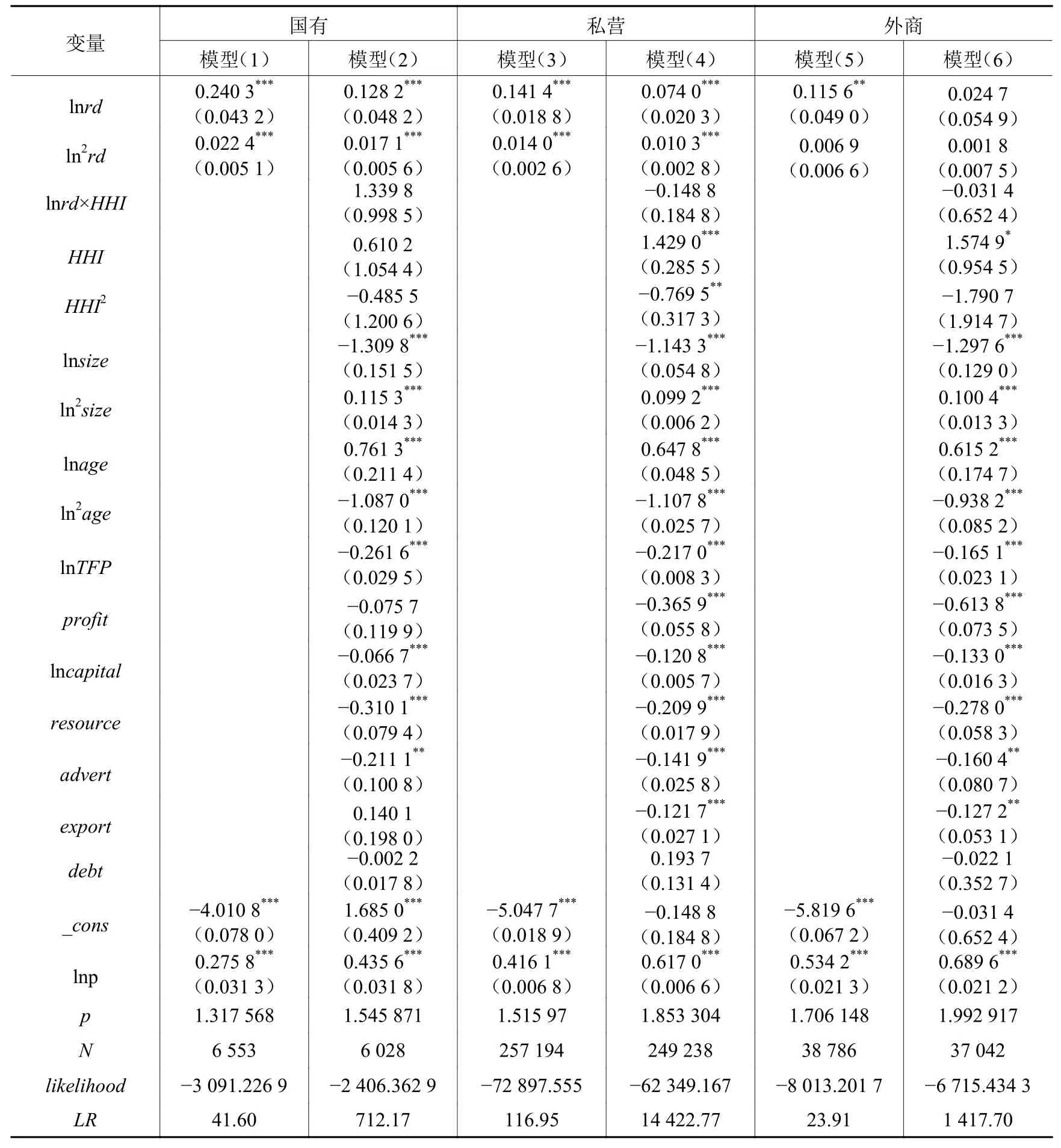
表 6 不同产权性质企业的回归结果

（四）稳健性检验

首先，分别采用销售收入和资产总额作为企业规模的衡量指标进行稳健性检验，并且分别用工业品出厂价格指数和固定资产投资价格指数对两个指标进行平减。表7显示的回归结果与基准回归结果一致。采用Logit、Probit和Cloglog模型的回归结果仍与Weibull生存分析模型的回归结果一致。

其次，上述估计结果的可信性是建立在企业生存不影响创新行为基础之上的。现实中企业生存风险的增加也可能迫使企业加大创新投入力度，因此有必要采用工具变量（IV）法解决可能的内生性问题。本文选取房价作为工具变量，这是因为：一是房价上涨会刺激企业将稀缺资源配置于投资回报率较高的房地产投资，同时高房价会导致创新人才从当地流出，从而不利于当地企业的技术创新（余泳泽和张少辉，2017；孔东民等，2018）；二是城市的房价并不会直接影响企业生存，但房价的普遍上涨可能会引起劳动力成本的上涨，从而间接影响企业生存，因此我们把人均工资作为控制变量纳入计量模型。本文的房价数据来自CEIC数据库的全国287个地级市商品房销售价格，在实证分析中采用两阶段最小二乘法（2SLS）进行估计，Hausman检验也证明了研发强度的内生性。

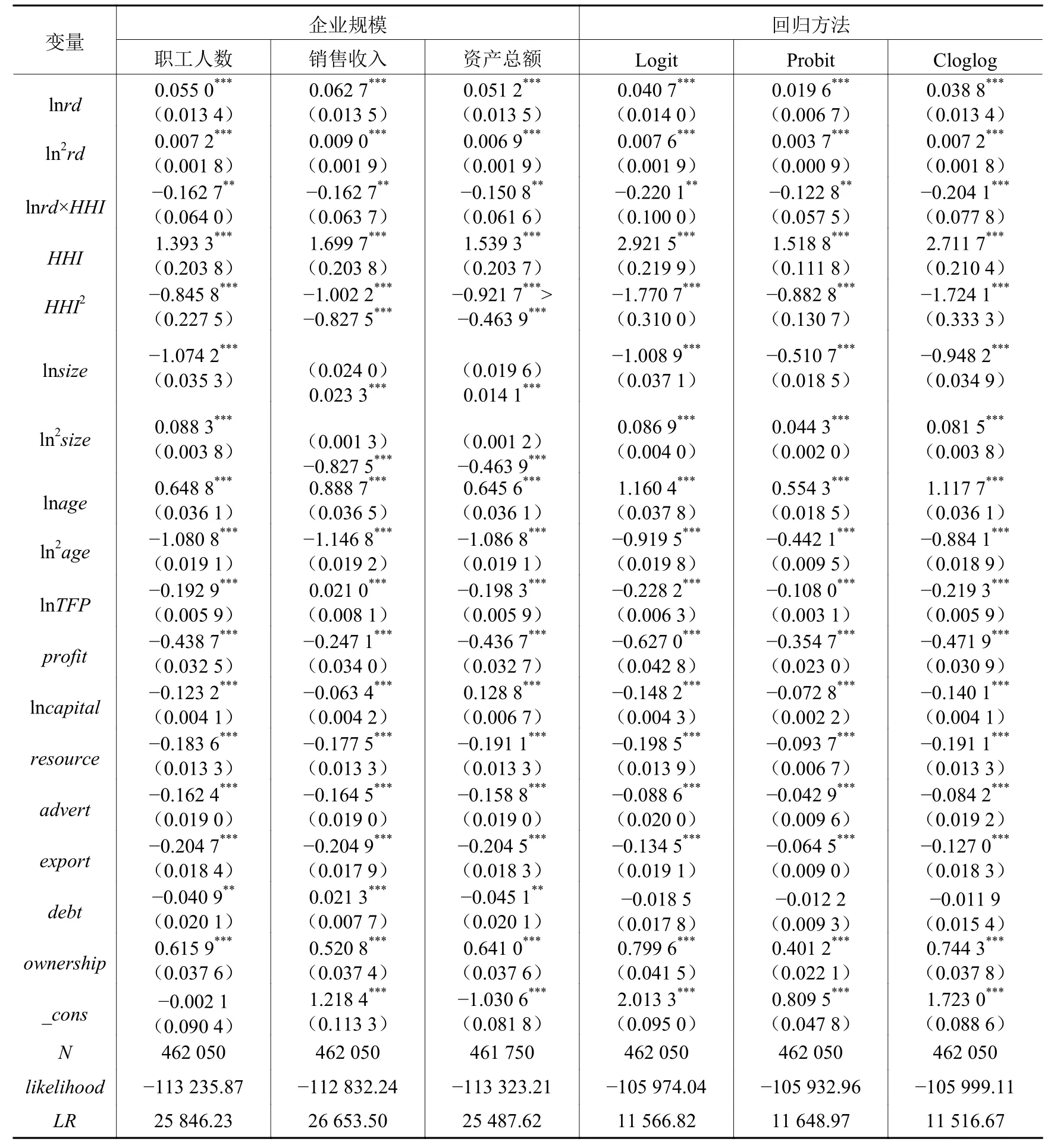
表 7 技术创新与企业生存：稳健性检验（1）

回归结果如表8所示：模型（1）是面板数据的OLS回归结果；模型（2）是工具变量下的2SLS回归结果，系数符号与OLS结果一致。为验证工具变量选取的合理性，引入弱工具变量检验，即模型（3），回归结果与模型（2）非常接近，表明不存在弱工具变量；模型（4）是工具变量固定效应的估计结果，符号仍与之前一致。因此，本文的结论依然是稳健的。

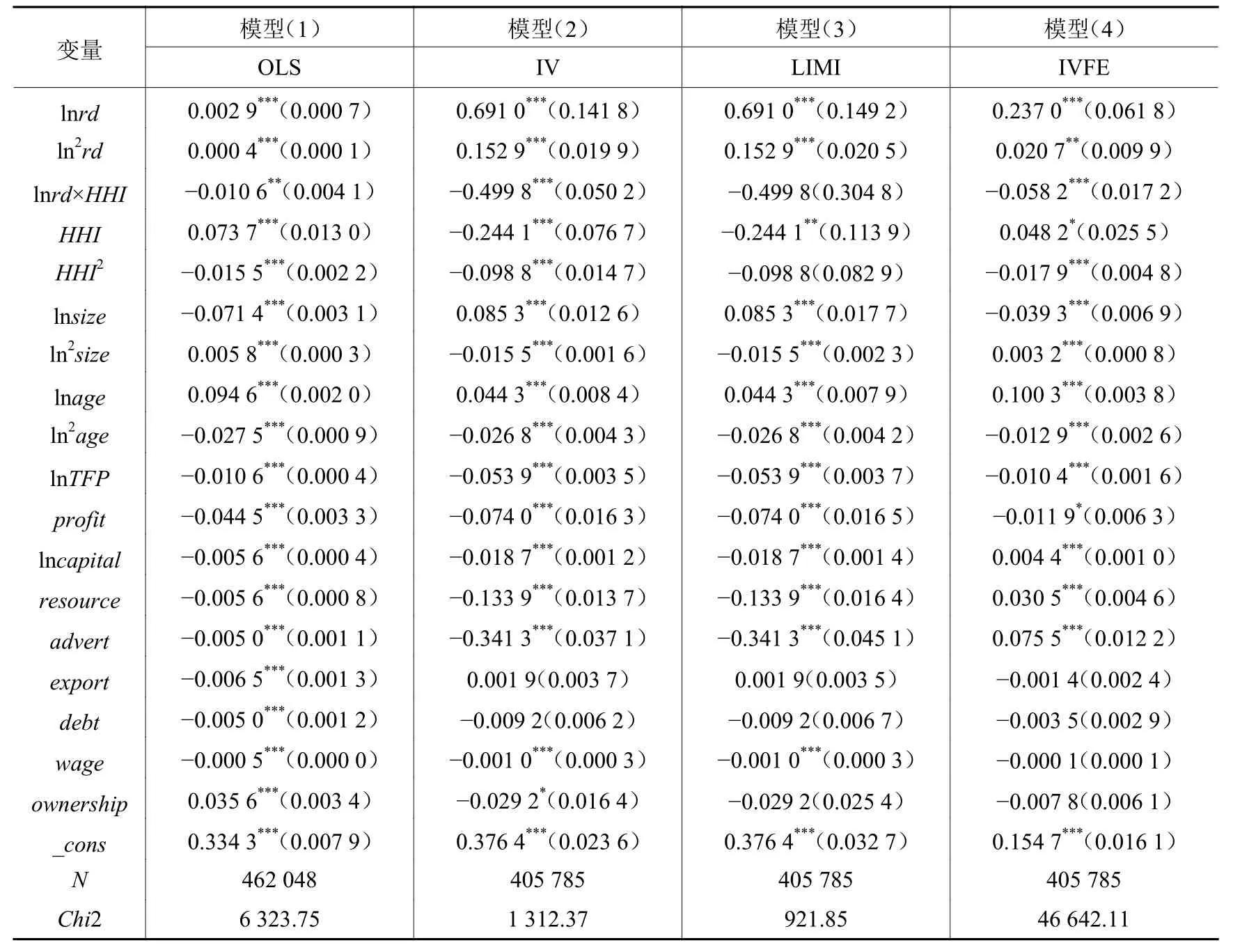
表 8 技术创新与企业生存：稳健性检验（2）

六、结论与启示

技术创新是影响企业生存的重要因素。本文通过构建熊彼特主义竞争与创新理论模型，采用国家统计局的全部国有及规模以上非国有工业企业数据库数据，选取Kaplan-Meier乘积极限法及Weibull生存风险模型，实证研究了创新对初创企业生存的影响。研究发现：（1）研发强度与企业生存之间呈规模效应递减的倒U形关系，即研发强度存在一个最优水平，在达到最优水平之前，生存时间随研发强度的提高而增加，达到最优水平之后，生存时间随研发强度的提高而减少。（2）研发强度和市场集中度对企业生存时间的影响是互补的，高集中度产业的企业存活时间更长。（3）创新和企业生存的关系还受到行业技术水平和产权性质的影响。高技术产业的企业生存风险率更低；国有企业的研发水平较高，但其生存风险率却高于非国有企业。此外，其他变量如企业年龄、企业规模、全要素生产率、销售利润率、资产负债率的影响，与既有文献研究结论基本一致。

本文的启示在于：一方面，其他条件不变的情况下，实现初创企业生存时间最大化存在一个最优的研发强度水平，但这个最优水平可能会受行业技术水平、企业产权性质等影响。如何决定研发强度最优水平是企业管理者必须思考的问题。从长远发展看，企业应当把创新作为发展的主战略，努力提高技术创新水平，通过创新活动提高核心竞争力，从而延长企业存活时间。另一方面，政府在大力倡导“大众创业、万众创新”的同时，应关注初创企业的生存问题，建立初创企业生存率的检测体系，特别要注意不同行业技术水平和产权结构的企业存活的差异，对初创阶段的非高技术行业的企业和私营企业经营风险进行辅导，或者在必要时候能够提供适当支持，以促进初创企业的生存与发展。