定积分在极限中的应用

（安徽信息工程学院，芜湖 241000）

引 言

极限内容是高等数学重难点之一，而关于极限的和式极限，往往不太容易得出结果，这对于学过定积分的人来说或许是个优势，就是将和化成积分，而一般教材中没有对此内容进行单独讲解，而考研或者竞赛中往往会涉及到此类问题，一些基础薄弱的学生，很难从和化定积分方面，来求解该类极限。本文将从简单的例子逐步分析，方便读者掌握。

一、区间n等分的极限化定积分

（1）首先回顾下定积分定义，设f为区间[a，b]上的连续函数，若f恒大于0，在[a，b]上取（n-1）个分点，记为 a=x0＜x0＜x1＜…＜xn=b，此时区间被分成 n 个小区间 [xi-1，xi]i=（1，2……n），为第i个矩形面积，将所有矩形面积作和式，，q=max｛△xi｝，则，若取a=0，b=1，给区间进行n等份，则。

（2）可化为定积分极限题型

①直接对和式极限进行转化。

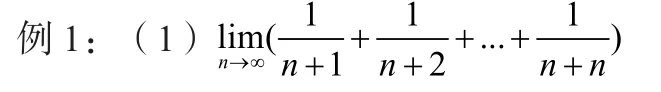
分析：若用学过的知识求解，例如极限定义，显然这边有无穷多项不太适合；利用放缩法则也不好对整体进行代换，洛必达更行不通。这时候用定积分定义恰巧可以解决问题。

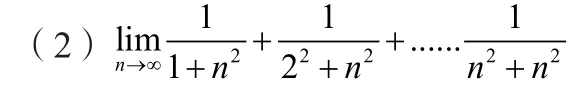
②改写原极限成和式。

母亲在我面前替父亲说好话。母亲说起那年那场大雪，父亲原是准备坐轮船去上海的，却得到我患病的口信，连夜往家赶。路上用他最钟爱的口琴换了两只橘子带给我。大雪漫天，没有可搭乘的车辆，他就一路跑着。过了江，好不容易拦下一辆装煤的卡车……

分析：该题看上去与和式极限没关联，但是一般情况下，得要进行变换，使得它成为和式极限。

首先还是改写极限将原式变形：

分析：我们步骤模仿（1）问进行解题即可。具体步骤如下所示：

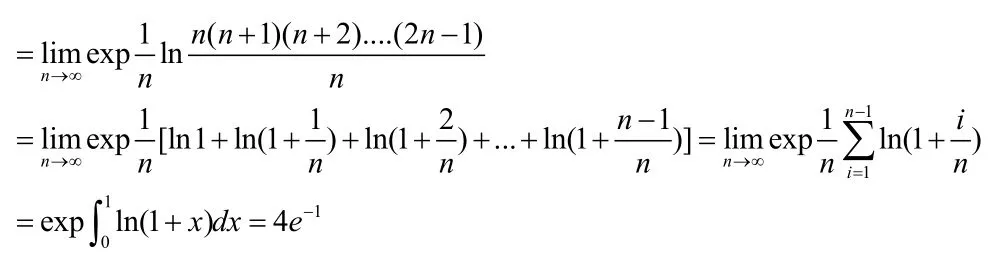
该类题型稍微进行了一点变换，但最终还是用定积分定义巧妙解决。

③基于两边夹法则改写和式

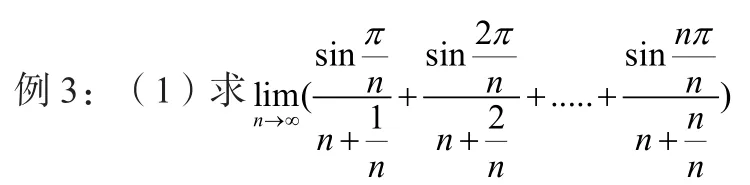
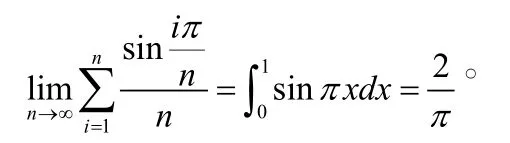
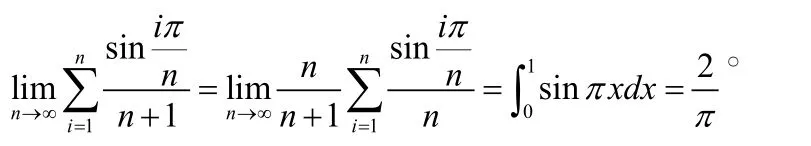
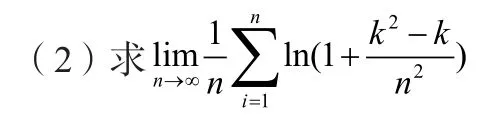
分析：该极限和上述类型相同，已经是和式，也很难找出λi，这时候我们仿照前一题用放缩准则，来进行两边夹，从而可以取到λi。

首先观察极限形式可以直接看出

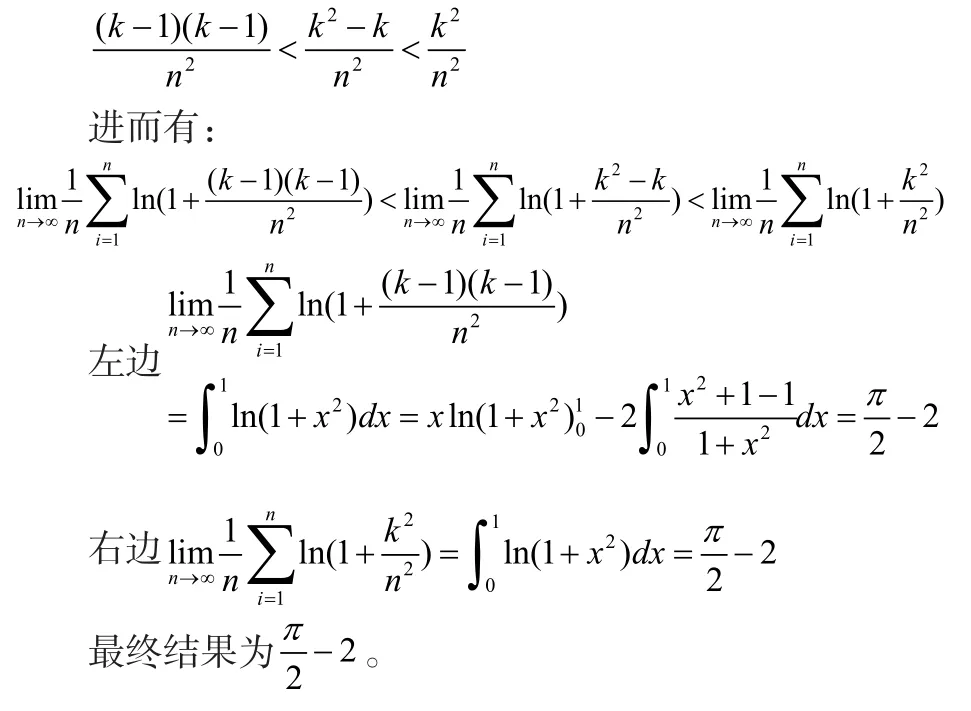
二、非n等份的极限化积分

分析：这里的和式如果看成（0，1）区间的n等份的话，不太容易计算，这里的和式，可以看成函数sinx在[1，b]按分划所作的积分和。

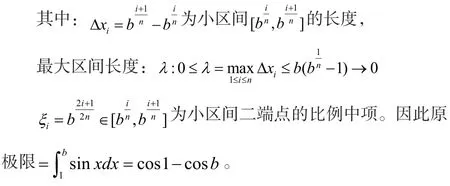
结 语

一般情况下，我们只需要了解并掌握好，n等分的极限化积分情况即可。最后一种情况超过考研范围。感兴趣的读者可自行研究。