决策树分类算法中C4.5算法的研究与改进①
2019-07-23韩存鸽叶球孙
韩存鸽,叶球孙
1(武夷学院 数学与计算机学院,武夷山 354300)
2(认知计算与智能信息处理福建省高校重点实验室,武夷山 354300)
决策树分类算法是分类挖掘算法中较为常用的算法,是一种自顶向下的递归算法,常用于分类器和预测模型.1966年Hunt 等人开发研制的CLS[1]系统,为许多决策树算法奠定了基础.1979年Quinlan 提出ID3[2]算法,其核心思想以最大的信息增益属性作为分裂属性.之后的许多决策树算法都是在ID3 算法的基础上衍生改进的.其中C4.5[3]算法就是在 ID3 算法的基础上发展的,采用信息增益率作为属性选择的度量依据,在处理连续性属性的时,C4.5 算法将这些连续属性“离散化”,解决了ID3 算法多值偏向性的缺点,有效避免了取值较多的属性容易被选作分裂属性的趋势,增强了决策树模型的有效性.但是当测试集属性值缺失率高时,C4.5 算法的分类准确率会明显下降,而且在构造树的过程中,该算法需要多次对数据集进行顺序扫描及排序,在进行计算时又频繁地调用对数,增加了算法的时间开销,从而导致算法低效[4].
文献[5]调整了连续阈值惩罚项,但是并没有解决决策树过度拟合问题.文献[6]提出双重熵平均决策树算法,采用熵值拟合的方法,提高算法运行速度,但是没有解决空缺属性问题.文献[7]在连续属性离散化方面进行了改进,但并没有很好的解决过度拟合问题.文献[8]适用范围为变精度粗糙集,不适合一般数据分析.
本文在研究C4.5 算法的基础上提出一种优化算法,通过对UCI 数据库中 5 个数据集进行实验,实验结果表明,改进后的算法极大的提高了运行效率.
1 C4.5 算法理论
C4.5 算法是在ID3 的基础上加进了对连续型属性、属性值空缺情况的处理,通过生成树和树剪枝两个阶段来建立决策树.C4.5 算法通过计算每个属性的信息增益率(information GainRatio),最后选出具有最高信息增益率的属性给定集合S 的测试属性,再根据测试属性值建立分支,采用递归算法,得到初步决策树.C4.5 算法的相关计算公式如下[9]:
(1)期望信息(也称信息熵)设S是Si个数据样本的集合,假定类标号属性有m个不同值,定义m个不同类Ti(i=1,…,m).设Si是类Ti中的样本数.对一个给定的样本分类所需的期望值为:

(2)信息增益 由属性A划分成子集的信息量为:

信息增益为原来的信息需求与新的需求之间的差.

(3)信息增益率C4.5 算法中引入了信息增益率,属性A的信息增益率的计算公式为:

C4.5 算法采用后剪枝技术对生成的决策树进行剪枝操作,形成决策树模型,根据建立好的模型,生成一系列IF-THEN 规则,实现对训练集的分类.
2 改进的C4.5 算法
2.1 决策分类过程中空缺属性值处理研究
(1)延伸贝叶斯分类算法
决策树进行分类时,测试样本数据中可能存在缺失某些属性值.传统的决策树算法在处理缺失属性值时,一般采用抛弃缺失属性值的样本,或重新赋予训练样本该属性的常见值[10].C4.5 算法采用概率分布的填充法来处理缺失属性值,具体执行过程:首先为某个未知属性的每个可能值赋予一个概率,根据某节点上属性不同值的出现频率,这些概率可以再次估计[11].虽然C4.5 算法有很强的处理噪声数据的能力,但当训练集合属性值的缺失率很高时,使用该算法构建的决策树模型的结点数更多,模型更为复杂,而且分类准确率也会下降[12].鉴于朴素贝叶斯分类具有坚实的理论基础、较小的出错率.本文提出一种基于朴素贝叶斯定理方法[13],来处理空缺属性值.
假设数据样本为n维向量空间,V={V1,V2,V3,…,Vi} 若该数据样本有C1,C2,C3,…,Cm个类别属性取值,那么基本贝叶斯将未知类别的样本V归到类别Ci,当且仅当:

等价p(ci)p(v|ci)>p(cj)p(v|cj).
若V的m个属性互相独立,那么

继而推出:

故将未知类别的样本X归到类别Ci,当且仅当

根据上述原理可以实现对多维空缺属性的处理:

(2)空缺属性值处理过程
本文采用上述算法处理空缺属性,大致流程如下:
① 读入测试数据.
② 若数据集中没有空缺属性值,则把数据压入Di集合;如果测试数据集中含有空缺属性值,采用“样本空缺属性个数排序,越少越排前,反之则排后.”的原则插入到D2集合.
③ 返回第一步,直到测试数据集中所有数据都检测结束.最后形成Di、D2两个集合.其中Di中存放没有空缺属性值,D2中存放包含空缺属性的信息.
④ 取出D2中的记录数据,为缺失属性赋值计入Di.
⑤ 递归调用上述第④步,直到D2中记录为0.
2.2 改进思想及改进计算方式
虽然C4.5 算法具有建模速度快、准确率高、易于理解、灵活简单等优点,但是该算法在构造树的过程中,需要多次对数据集进行顺序扫描及排序,在进行计算时又频繁地调用对数,增加了算法的时间开销,从而导致算法低效.针对以上缺点,本文对C4.5 算法的计算公式进行精简优化,从减小计算时间上提出一种改进算法命名为N-C4.5 算法.公式简化如下:
假设S是n维有穷离散数据集,S中只有正反两种情形,分别表示为YS 、NS,其中正例YS 的记录数为m,反例NS 的记录数为n,根据式(1)数据集S分类所需的期望值为:

假设决策树的根为A属性,A属性的取值为{A1,A2,…,Ai},利用属性A将数据集S分为{S1,S2,…,Si}个子集,其中Si为S中属性A取Ai值的样本实例数据,那么由属性A划分成子集的信息量为

在数据集D中计算属性X的信息熵公式为

根据无穷小原理l n(1+x)≈x,那么:
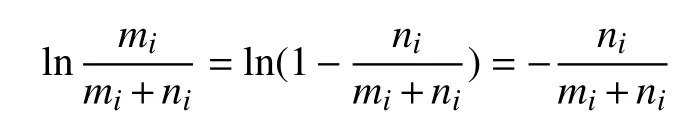

信息增益:Gain(A)=Info(S)-In foA(S).

改进后的计算公式使用四则混合运算代替原来的对数运算,可以使计算效率得到提升.原C4.5 算法的时间复杂度为O(n2logn2),改进后的算法时间复杂度为O(n2),新算法去掉了对数运算,优化了时间复杂度.
2.3 N-C4.5 算法实际应用
为了验证算法正确性,这里以顾客购买计算机的样本信息S为例,具体样本记录如表1所示.使用改进后的算法构建决策树,命名为N-C4.5 算法.该数据集S 有age、income、student、credit_rating、buy 5 个属性,其中buy 为类标号属性,有两个取值{yes,no},S数据集的前4 个属性为分裂属性,并且每个属性都是离散化的.这里根据每个人的age、income、student、credit_rating 来进行分类,判断顾客是否购买计算机.

表1 顾客购买计算机的样本信息S
对客户购买计算机的样本信息按照改进以后的算法构建决策树,利用改进后的公式计算信息熵、信息增益、分裂信息量、以及信息增益率,同时选择最大信息增益率作为分裂结点,采用递归算法构建决策树.在数据集S中属于类别“yes”的有9 个,属于类别“no”的有5 个,根据改进后的公式计算过程分如下五步.
Step1.计算分类所需的期望信息

Step2.计算每个属性的信息熵

Step3.计算每个属性的信息增益

Step4.计算每个属性的分裂信息度量
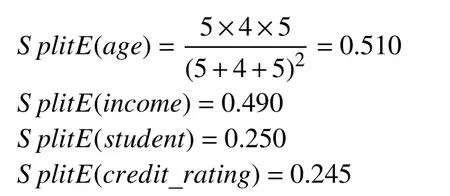
Step5.信息增益率

由计算结果可知,age 属性的信息增益率最大,所以选择age 作为分裂属性,将原数据集分为youth、middle、senior 三个子集,采用递归算法计算每个属性的信息熵、信息增益、分裂信息量、信息增益率,对于youth 子集,经计算得出student 信息增益率最大,选择student 作为测试属性;对于middle 子集全部归为yes 类,所以不需要进行分类;而对于senior 子集,通过计算得知,credit_rating 信息增益率最大,因此选择credit_rating 作为测试属性,根据所有结点,可以得出购买计算机数据集采用N-C4.5 算法构造的决策树如图1.
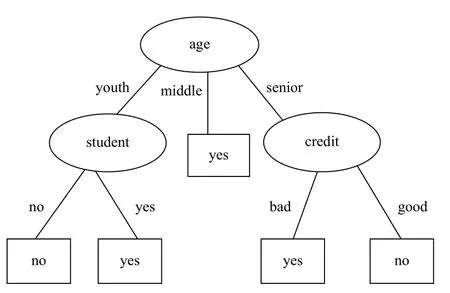
图1 N-C4.5 算法构造的决策树
由图1可以看出采用N-C4.5 算法构造的决策树与使用原C4.5 算法得到的决策树结构完全相同,但C4.5 算在计算的过程中调用了大量的对数,而NC4.5 算法却只需要采用简单的混合运算即可,因此运算效率大幅度提高.
3 实验结果比较分析
为了验证N-C4.5 算法的性能,本实验选择UCI 数据库中 5 个数据集进行仿真实验,实验数据的基本信息见表2,实验硬件配置:内存 4 GB,CPU 2.50 GHz ,使用Window7 操作系统,采用Java 语言在WEKA 平台中进行仿真实验.仿真实验时,首先利用延伸的贝叶斯分类算法填充多维空缺属性,该方法会生成空缺属性的各种可能取值组合,接着遍历各种组合,按公式计算值并记录最大值即可;然后利用改进后的公式计算信息熵、信息增益、分裂信息量、以及信息增益率,最后选择最大信息增益率作为分裂结点,采用递归算法构建决策树.

表2 测试数据集基本信息
Iris 数据集是构建决策树挖掘中最典型的一组数据,共有150 条记录,有4 个分裂属性,类标记属性为3 种,人为添加部分缺失信息,缺失属性为sepal width,共有30 条缺失记录,使用Iris 数据集对改进前后的算法进行5 次仿真实验,实验结果如图2所示.

图2 Iris 数据建模时间
由图2可以看出,对于Iris 数据,N-C4.5 算法的运行时间短,优化效果明显.为了验证N-C4.5 算法算法的效率,对于其他4 组数据集,同样都分别使用改进后的N-C4.5 算法与C4.5 算法进行仿真实验,测试时每个数据集都运行5 次,建模时间取5 次的平均值,建模时间如表3所示.

表3 建模信息表
由表中可以看出,数据样本的大小会影响算法的运行时间,一般情况下,测试数据样本数据量越大,需要运行的时间越长.算法改进前后的比率都大于1,正确率的提升都是正值,可以得出结论:N-C4.5 算法的建模时间明显优于C4.5 算法,分类准确率也高于原C4.5 算法.
4 总结
虽然C4.5 算法具有建模速度快、准确率高、易于理解、灵活简单、以及处理噪声数据的能力强等优点,但当属性值缺失率高时,分类准确率会明显下降;在构建决策树时,需要多次扫描、排序数据集、以及频繁调用对数等缺点.本文提出一种改进的决策树分类算法.采用一种基于朴素贝叶斯定理方法,来处理空缺属性值,提高分类准确率.通过优化计算公式,改进后的N-C4.5 算法使用四则混合运算代替原来的对数运算,减少构建决策树模型的运行时间,使计算效率得到提升.
