应变软化土坡基于分层技术的有限元计算

乐巧丽

（贵州民族大学 建筑工程学院，贵州 贵阳 550000）

对于应变软化边坡来说，滑动面上各土体的强度不会同时达到峰值强度，部分土单元先达到峰值强度，发生局部破坏，而破坏后的土单元发生了软化现象。以H8边坡为例，利用ABAQUS软件建立计算模型，通过分层技术考虑应变软化性质，再采用强度折减有限元法计算出结果，与采用峰值强度指标和残余强度指标的有限元计算结果进行对比，分析评价该边坡的稳定性。

1 工程概况

H8边坡坡度为30°～55°，水文地质条件较简单，没有不良的地质现象。该处的地层主要包括：①坡积层，以砾粉质黏土为主；②滑坡堆积层，大多数是粉质黏土，结构松散；③冲积层，含有砂黏性土、黏土。

2 模型的建立

根据H8边坡的勘察资料，用ABAQUS软件建立边坡模型，如图1所示。模型中的土层参数为：重度γ=20 kN/m3，E=50 MPa，μ=0.3，cp=20.6 kPa，φp=25°，cr=5 kPa，φr=25°。

3 有限元计算

3.1 采用峰值强度指标的有限元计算

通过ABAQUS软件建立如图1所示的边坡模型，模拟计算时将土体强度指标设置为cp=20.6 kPa，φp=25°，采用摩尔—库伦模型，采用强度折减有限元法进行计算。

选择坡顶节点为分析节点，模拟结果显示，坡顶节点的总位移U、水平位移U1及竖直位移U2和安全系数之间的关系如图2所示。

从图2可知，当安全系数为1.231时发生了位移突变。利用边坡失稳判据可知，该边坡的安全系数Fs=1.231。

3.2 采用残余强度指标的有限元计算

同样，利用ABAQUS软件建立图1所示的边坡模型，模拟计算时土体强度指标采用cr=5 kPa，φr=25°，其余代入的参数与3.1中的相同，进行模拟计算。模拟结果显示，当增量步时间t=0.152 s时，模拟计算就不收敛了，利用计算不收敛失稳判据，可得该边坡的安全系数Fs=0.728。

3.3 考虑应变软化性质的有限元计算

利用ABAQUS软件建立模型图，如图3所示。

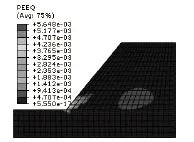
图3 自重作用下边坡的塑性应变图

模型中参数的设置与3.1节相同，利用有限元模拟出边坡在自重作用下产生的PEEQ（塑性应变）。

PEEQ（Avg：75%）改为塑性应变（平均值为75%）

从图3可看出，局部土体在自重作用下产生了较大的变形，发生了软化现象。为了考虑应变软化性质对边坡稳定性的影响，现对发生了软化的局部土体进行分层处理，如图4所示。其中，②③层视为软化层，各层的材料参数根据等效塑性应变的大小进行相应的取值，如表1所示。

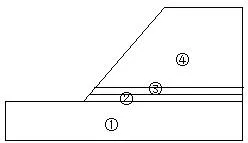
图4 分层后的边坡模型图

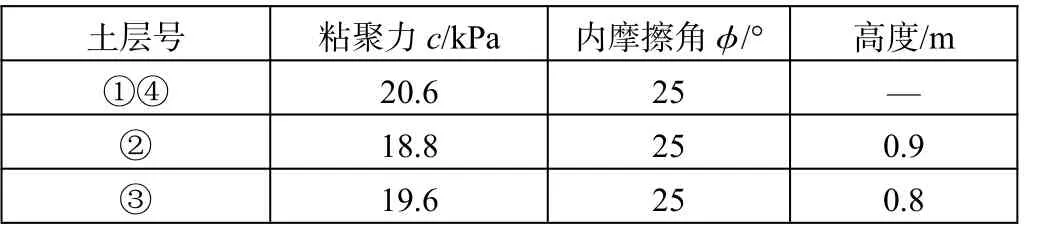
表1 土层的材料参数

利用强度折减有限元法模拟分析图4所示的边坡。坡顶节点的水平位移U1和安全系数Fs之间的关系如图5所示。

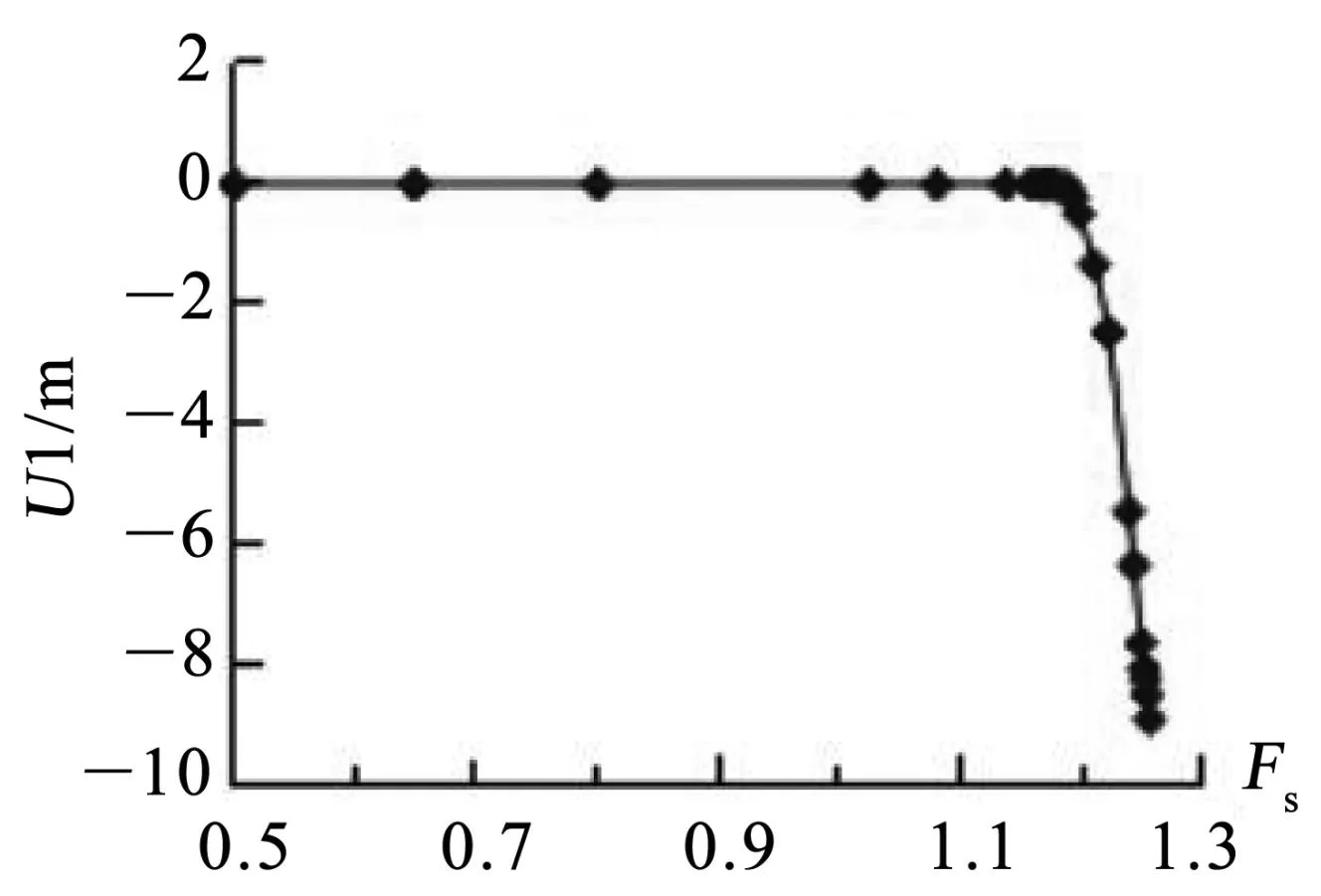
图5 坡顶节点的U1和Fs曲线图

从图5可看出，在安全系数为1.187时，坡顶节点处发生了位移突变现象，因此可知，该边坡的安全系数为1.187。

4 结论

通过上述的有限元模拟计算，分别获得了三种情况下的边坡安全系数，如表2所示。从表2看出，采用峰值强度情况计算得到的安全系数最大，容易高估边坡边坡的稳定性；采用残余强度情况计算的安全系数最小，容易低估边坡的稳定；而考虑应变软化情况计算得到的安全系数介于两者之间，与边坡的实际情况更相符，可以更好地评价边坡的稳定性。

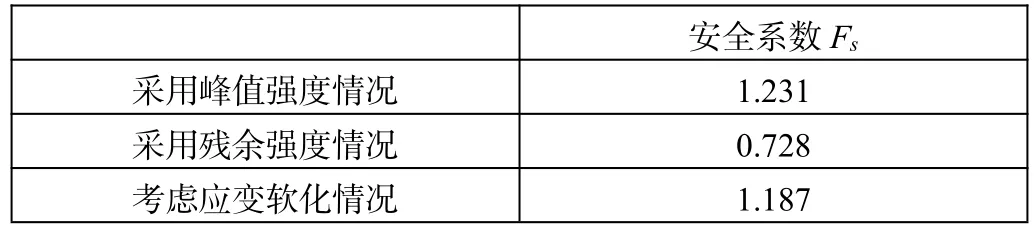
表2 基于三种情况下的安全系数