球分布形式对角接触球轴承径向游隙测量误差的影响
2019-07-22王东峰陈静张晓鹏方萍张红英
王东峰,陈静,张晓鹏 ,方萍 ,张红英
(1.洛阳轴承研究所有限公司,河南 洛阳 471039;2.河南省高性能轴承技术重点实验室,河南 洛阳 471039;3.高性能轴承数字化设计国家国际科技合作基地,河南 洛阳 471039;4.北京航天控制仪器研究所,北京 100854)
符号说明
B——轴承宽度
d——轴承内径
D——轴承外径
DGF——2个相邻球间距的一半
Dpw——球组节圆直径
Dw——球径
E——轴承外沟道直径
F——轴承内沟道直径
fi——轴承内沟曲率半径系数
fe——轴承外沟曲率半径系数
g1——轴承外圈单向移动量
g2——球呈四边形分布时的外圈单向移动量
Gr——角接触球轴承径向游隙
Grmax——角接触球轴承最大径向游隙
Z——球数
α——接触角
ΔGr——轴承径向游隙变化量
ΔGr0——球分布形式引起的径向游隙变化量
ΔGrH——壁厚引起的径向游隙变化量
ΔGrM——实测径向游隙变化量
ΔH——测量载荷引起的套圈变形量
径向游隙对角接触球轴承的综合性能具有十分重要的影响,安装和运行条件一定时,径向游隙决定着轴承的载荷分布、最大接触应力,进而决定着轴承的疲劳寿命。因此,径向游隙是轴承装配合套、安装配合、运行维护阶段的重要技术参数,是生产、应用过程中的必检项目。但由于轴承内部结构、测量仪器的局限性,以及环境、人员技能水平的综合影响,径向游隙的测量精度一直是精密角接触球轴承的技术难点。
1 角接触球轴承径向游隙测量原理
角接触球轴承径向游隙计算公式为
Gr=E-F-2Dw。
(1)
轴承行业一般采用X095A仪器检测角接触球轴承的径向游隙[1],如图1所示。测量时,将内圈固定在芯轴上,向外圈施加规定的测量载荷,使外圈从一个径向极限位置移动到相反的径向极限位置,百分表示值所反映的移动距离即径向游隙。施加载荷的目的是为了保证测量过程中轴承各零件处于接触状态。

1—下载荷加载压滚;2—可换芯轴;3—紧固螺钉;4—压板;5—被测轴承;6—上载荷加载压滚;7—测头;8—百分表;9—同轴杠杆;10—仪器支座
检测过程中,示值误差、指示表分辨力、数据修约、样品测试重复性等参数引入的不确定度分量均很小[2];同时,环境温度变化,内、外圈相互偏转,以及测量载荷引起的球与沟道的接触变形等因素对检测结果的影响也极小[3]:这些影响因素在实际检测过程中可以忽略不计。因此,尝试分析在不同的球数、接触角、壁厚等条件下,球分布形式对角接触球轴承径向游隙测量误差的影响。
2 球分布形式对径向游隙测量误差的影响
在进行角接触球轴承(包括满装角接触球轴承)径向游隙测量时,球相对于测头的分布形式可以定义为直线形、三角形和四边形这3种基本形态,如图2所示。直线形分布时,符合测量仪器设计的阿贝法则[4],在忽略球与沟道的接触变形以及球与保持架兜孔间隙引起的极小偏移量对径向游隙测量的影响之后,其测量结果是最准确的;三角形分布时会有一端测头处于空位状态,四边形分布时两端的测头均处于空位状态,空位状态会导致轴承外圈移动量增大,从而导致较大的测量误差。由图可以看出,直线形和四边形是角接触球轴承径向游隙测量时的2种极限状态,可以认为这2种状态间的测量差值就是由球分布形式引起的径向游隙测量误差。

图2 角接触球轴承球分布形式示意图
不考虑测量载荷对套圈变形的影响,分析带保持架角接触球轴承的径向游隙变化量。球呈直线形分布时,径向游隙如图3a所示。空位状态下测量时,由于重力和球的推力,保持架有一个偏移量;同时,由于保持架兜孔比球径大,球在保持架兜孔中也有一个偏移量。球和保持架的偏移量会使轴承外圈产生偏移量,导致径向游隙的增大。
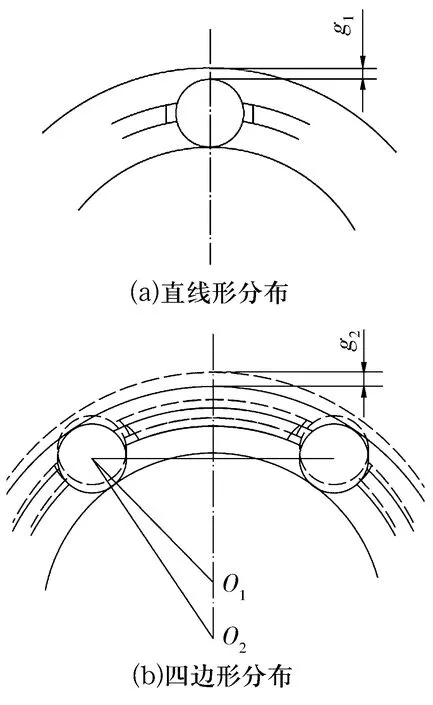
图3 径向游隙变化示意图
如图3b所示,对轴承空位一端进行径向游隙测量,其移动量为
(2)
(3)
E=Dpw+[2fe-(2fe-1)cosα]Dw,
(4)
F=Dpw-[2fi-(2fi-1)cosα]Dw。
(5)
因此,设g1为轴承径向游隙的一半,则当球呈三角形分布时,径向游隙实际测量值为
Gr=g1+g2,
(6)
当球呈四边形分布时,径向游隙实际测量值为
Gr=2g2。
(7)
对于同一型号轴承,球分布为直线形和四边形时,测量得到的径向游隙值覆盖了轴承的整个游隙范围,则由于球的分布形式引起的径向游隙变化量ΔGr0为
ΔGr0=2(g2-g1)。
(8)
因此,重点讨论球分布为四边形时,轴承球数、接触角以及外圈壁厚对径向游隙变化量ΔGr0的影响。
2.1 球数对测量误差的影响
由(2)~(5)式可知,在接触角、球径给定的情况下,内、外圈沟道直径均为定值,DGF则只随球数的变化而变化,因此,若球数不同,径向游隙变化量也不同。令X1=E-Dw,X2=F-Dw,则球数变化引起的径向游隙变化量ΔGr0为
以7010AC/P4型角接触球轴承为例(基本参数见表1),假定其接触角保持25°不变,计算球数为5~30时轴承对应的径向游隙及其变化量,节选的部分数据见表2,径向游隙变化量随球数的变化如图4所示。
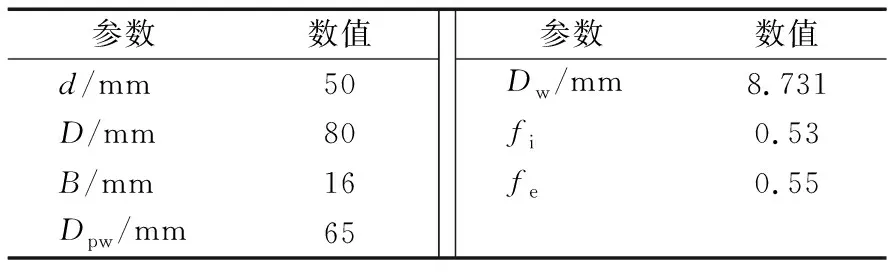
表1 7010AC/P4轴承的基本参数

表2 不同球数对应的径向游隙变化量
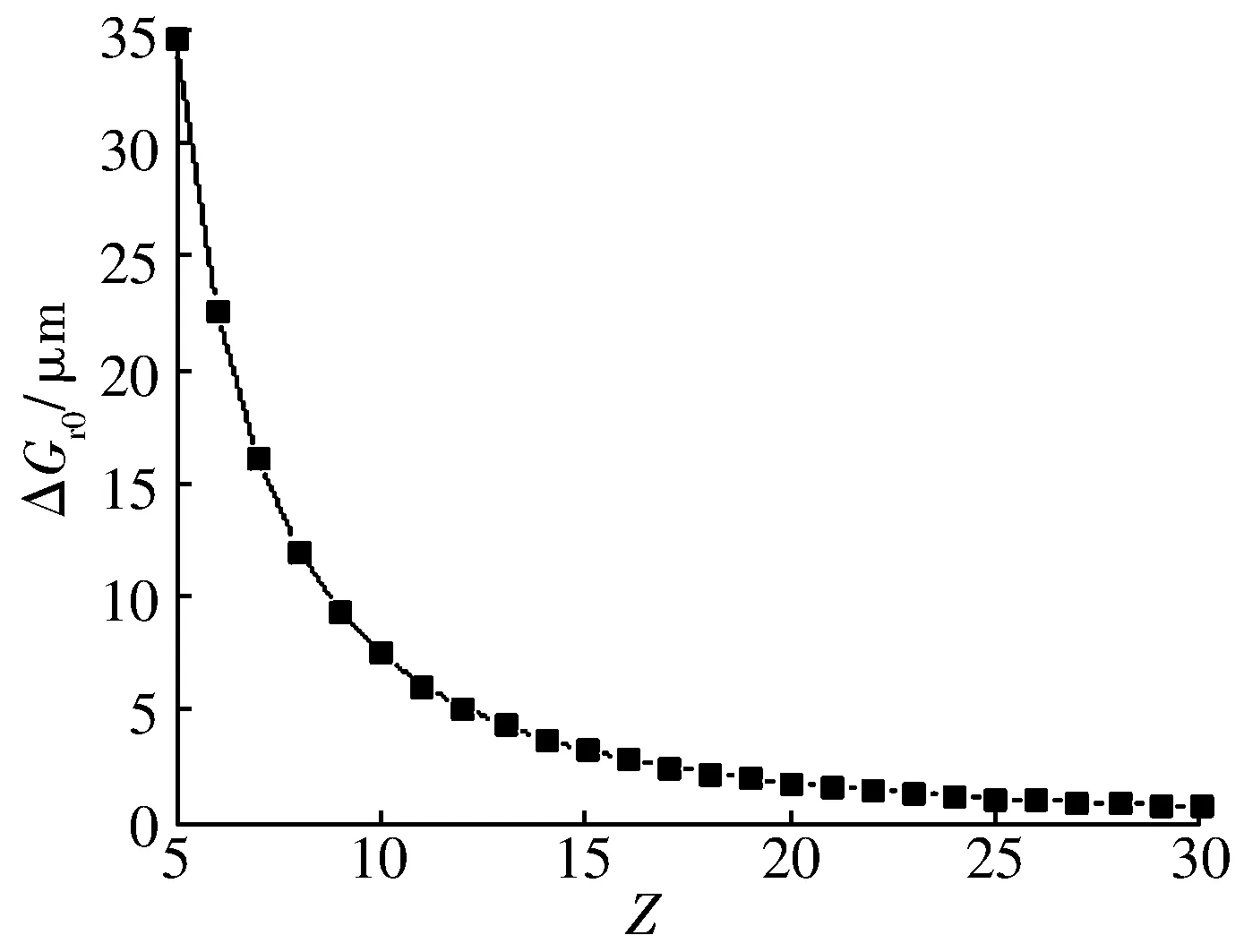
图4 球数变化对径向游隙变化量的影响
从表2及图4可知,当球数较少时,球分布形式对角接触球轴承径向游隙测量误差的影响非常大,如球数在5~10的阶段,径向游隙变化范围为0.005~0.035 mm;当球数超过20后,径向游隙变化量基本稳定在0.001 mm,可以近似认为径向游隙为恒定值,在实际生产中可以忽略不计。
2.2 接触角对测量误差的影响
由(2)~(5)式可知,在球数、球径给定的情况下,内、外圈沟道直径均随接触角的变化而变化,若接触角不同,径向游隙变化量也不同。
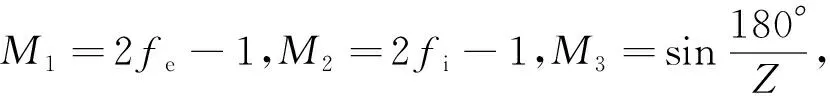
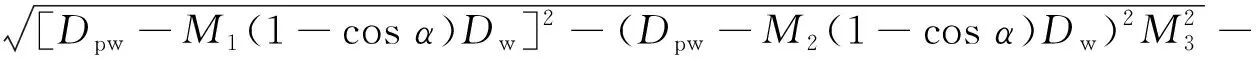
(10)
同样以7010AC/P4型角接触球轴承为例,假定球数保持14不变,计算接触角为10°~60°时,轴承的径向游隙及其变化量,节选的部分数据见表3,接触角对径向游隙变化量的影响如图5所示。
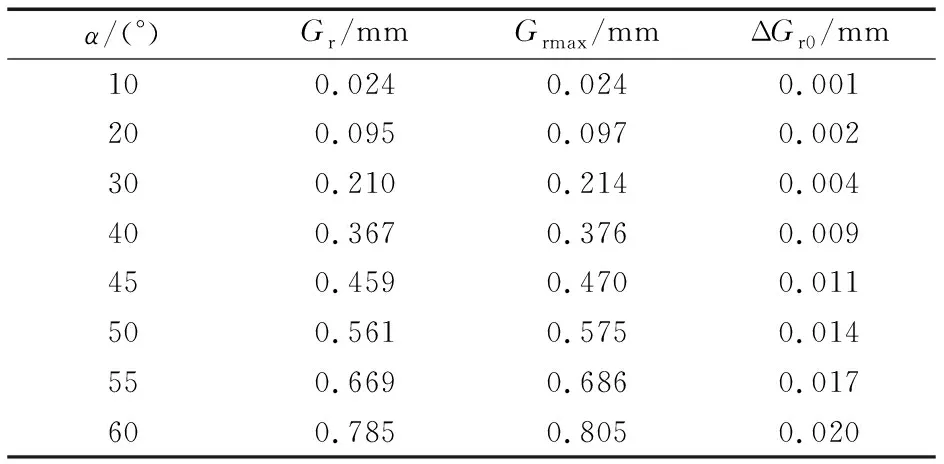
表3 不同接触角对应的径向游隙变化量
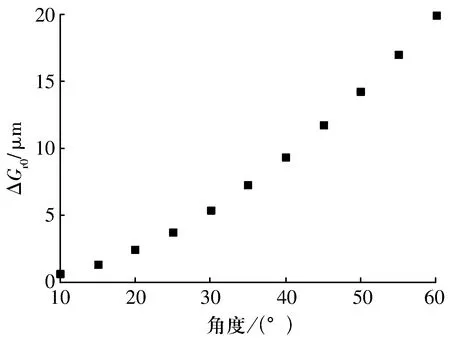
图5 接触角变化对径向游隙变化量的影响
分析可知,随着接触角的增大,径向游隙及其变化量也逐步变大;接触角小于15°时,接触角变化引起的游隙变化量较小,约0.001 mm,可以忽略不计;接触角超过25°后,径向游隙变化量则非常明显。
2.3 外圈壁厚对测量误差的影响
依据GB/T 25769—2010《滚动轴承 径向游隙的测量方法》,不同尺寸范围的轴承在进行径向游隙测量时需施加一定的测量载荷(表4)。如果测量时球的分布形式呈四边形分布,施加的测量载荷会导致轴承外圈产生较大变形(图6),对于同尺寸段内不同系列的轴承(如7200,7000,1800等系列),由于其承受测量载荷的外圈厚度不一样,其变形量会相差较大。

表4 不同尺寸范围轴承径向游隙测量载荷

图6 轴承外圈变形示意图
选取同一内径尺寸的角接触球轴承为例进行计算,假定球数为14,内径为50 mm,接触角为25°。利用ANSYS计算相同测量载荷(Fa=50 N)下不同壁厚轴承的外圈变形量,结果见表5。由表可知,在同一测量载荷下,由于外圈的变形量相差较大,导致径向游隙的测量误差也较大。
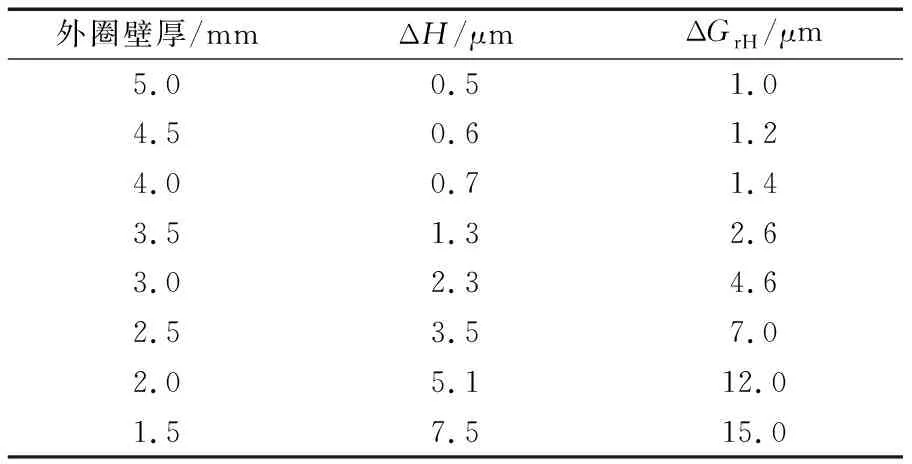
表5 外圈变形量及径向游隙变化量随套圈壁厚的变化
以表4给出的内径范围(8~200 mm)为例,利用ANSYS分别计算了不同测量载荷下轴承外圈壁厚为0.8~4.5 mm对应的变形量ΔH,结果如图7所示。
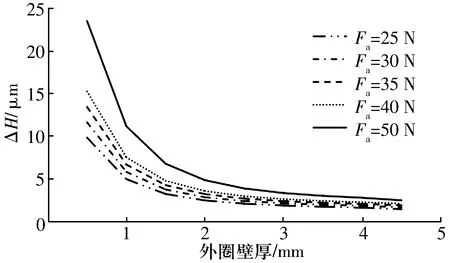
图7 变形量随测量载荷及壁厚的变化
从图7可以看出,不同内径尺寸范围在对应的测量载荷下,外圈变形量有明显区别。如内径范围为8~30 mm ,对应测量载荷为25 N,外圈壁厚从0.8增加到4.5 mm对应的变形量范围为0~0.01 mm;当内径范围为120~200 mm ,对应测量载荷为50 N,外圈壁厚从0.8增加到4.5 mm对应的变形量范围为0~0.025 mm(由于在一个尺寸段范围内,相同测量载荷和外圈壁厚对应的外圈变形量较小,研究中予以忽略)。因此,对于薄壁系列轴承,测量载荷引起的径向游隙变化量很明显,必须考虑测量载荷对径向游隙的影响。对于不同尺寸范围(不同测量载荷)、不同系列(不同壁厚)的轴承,先计算其外圈变形量ΔH,则对应的径向游隙测量误差为
ΔGrH=2ΔH。
(11)
2.4 球分布形式对径向游隙测量误差的综合影响
综上所述,在实际生产中,为了保证轴承的可靠性寿命和承载能力,一般都采取较多球数,因此,球数对径向游隙测量误差的影响很小,基本可以忽略不计。则球呈四边形分布时对各系列轴承径向游隙测量误差的综合影响主要包括接触角引起的径向游隙变化量以及套圈壁厚引起的径向游隙变化量,即
ΔGr=ΔGr0+ΔGrH。
(12)
以内径50 mm的不同系列标准角接触球轴承为例,不同接触角和壁厚对径向游隙的影响见表6。由表可知,理论上接触角和壁厚对径向游隙变动量的影响较大,特别是薄壁大接触角轴承,径向游隙变动量更为显著,该结果与实际产生的径向游隙测量误差ΔGrm(游隙测量值与设计值的差值)相吻合。因此,在实际径向游隙检测时,一般自由状态下非满装、正游隙轴承的球的分布多为四边形分布,也可以在测量时晃动保持架,让球呈自由四边形分布状态,在实际测量数值的基础上加上表6中给出的误差值ΔGr进行测量误差补偿,从而得到更为精确的径向游隙。

表6 不同接触角和不同系列轴承游隙测量误差对比
3 结论
1)球分布形式对角接触球轴承径向游隙测量误差有较大影响。四边形是角接触球轴承径向游隙测量时最常见的分布形式,其对径向游隙测量误差的影响也最大。
2)接触角对角接触球轴承径向游隙测量误差的影响也较大,随着接触角的增大,径向游隙变化量逐步变大,特别是接触角超过25°以后,径向游隙变化量非常明显,一定要避免球分布形式引起的测量误差。
3)由于测量载荷的作用,外圈会产生变形并导致径向游隙测量误差,该误差随外圈壁厚的减小而显著增大。
4)实际生产中,对于不同系列的标准轴承,需综合考虑球数、接触角和壁厚对径向游隙的影响,通过测量误差补偿得到精确的径向游隙。
