基于指令滤波的低频挠性航天器振动控制方法*
2019-07-22魏春岭王梦菲
魏春岭,袁 泉,张 军,王梦菲
0 引 言
随着空间任务要求的提高,越来越多的航天器要求进行姿态快速机动和稳定控制.然而,对于具有大型挠性附件的航天器来讲,快速机动会激起附件的振动,纵使姿态机动到位了,平台稳定度指标则长时间达不到载荷工作要求,错失工作时间窗口.因此对于带有低频大型挠性附件的航天器,研究其快速机动与稳定的控制方法,控制机动过程中其大型挠性附件的振动具有重要意义[1-2].
为了解决大型航天器机动时的挠性附件振动问题,国内外的学者提出了各种机动路径规划方法,主要包括:多项式规划法、正弦规划法、指数规划法等[3-4],从原理上讲,这些方法为工程化设计方法,主要是通过平滑姿态机动路径来减小挠性附件的振动.这些方法涉及的设计参数较多,主要是通过反复调整参数,然后仿真来验证机动效果,缺乏理论设计依据.
本文从本质上分析附件振动的原理,设计了一种基于滤波器的路径规划方法,该方法设计简单、鲁棒性强,通过物理试验验证了该方法能极大减小姿态稳定的时间,相比不采用挠性抑制方法时的100~1 000 s级的振动稳定时间,该方法能使姿态稳定时间降低到几秒钟量级.
1 系统模型
1.1 动力学模型
考虑一个中心刚体带n个挠性附件的航天器,对挠性附件进行有限元模态分析,第j个挠性附件的模态坐标可表示为ηj=[ηj1ηj2…ηjl]T.
星体的姿态动力学方程可表示为[5]

式中,Js为整星相对于质心的转动惯量,ωb为星体的姿态角速度,在本文中上标“×”代表相应三维列阵的反对称斜方阵,Abaj为从附件坐标系到本体坐标系的转换矩阵,Hj为星体中心体与挠性附件j的耦合矩阵,Cj为附件j的阻尼阵,Kj为附件j的刚度阵,Torq为作用于星体的控制力矩.
1.2 姿态控制算法
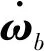
ωb=ωe+Abdωd(3a)
其中Abd为从期望姿态到星体本体姿态的坐标转换矩阵,ωe为误差姿态角速度.
将式(3)代入式(1),并整理得

其中:

星体的误差姿态满足下列运动学方程:


取控制器形式如下:
Tr=k1qe+k2ωe-
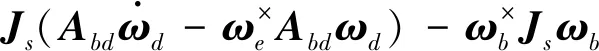
其中,k1,k2为正的常值.本文重点在于对姿态机动问题的研究,在此不对控制器的设计展开分析,该控制器的稳定性证明可见文献[6].
2 指令滤波设计方法
指令滤波设计方法的框图如图1所示.
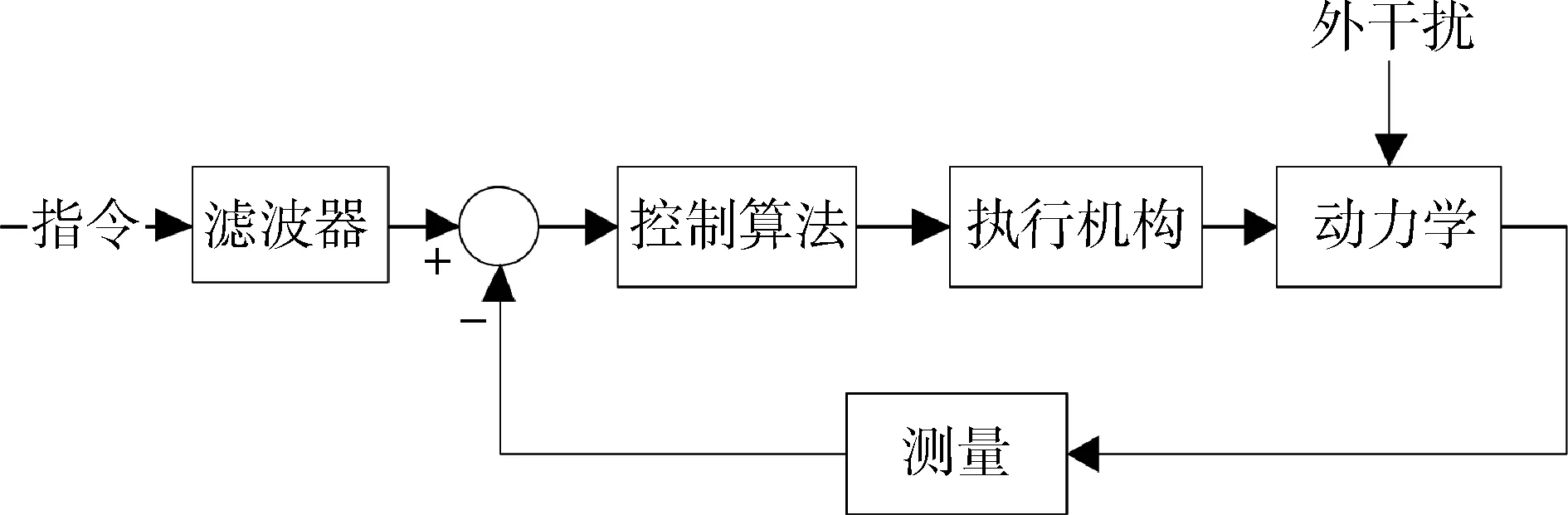
图1 指令滤波设计方法控制框图Fig.1 Illustration of Command Filter Method
考虑对挠性附件的振动抑制,挠性附件实际上是一个弱阻尼的二阶振动系统,它与航天器的耦合动力学方程可改写为如下式子:
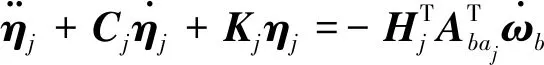

考虑机动时绕欧拉轴转动,设欧拉轴的方向余弦为VEuler,则有如下关系:

因此方程(8)可表示为

对a(t)设计如下形式的滤波器:

上述滤波器中,两个惯性环节是考虑执行机构、敏感器的惯性特性;两个二阶环节是考虑对挠性附件的振动抑制能力,其参数设计方法可完全参考惯用的结构滤波器设计方法,详见文献[7].不失一般性,可以根据实际需要,加入更多的一阶环节、二阶结构滤波器(如低通滤波器、陷阱滤波器).
一般在不考虑挠性影响时,Bang-Bang姿态机动过程中,机动路径按下列方式规划过程见图2所示.机动过程分为匀加速度段、匀速段、匀减速段.设匀加速度段加速度为常值a,加速度时间为Δt1;匀速时间段为Δt2-Δt1;匀减速段的加速度为常值-a,减速时间段也为Δt1.如图2所示,整个机动过程机动的角度为:

本论文提出利用设计的滤波器对上述Bang-Bang指令进行滤波.由于通过滤波的指令,已经考虑了执行机构、敏感器的动态特性,同时利用结构滤波器的思想,实现了对挠性附件的振动抑制.下面证明:只要合理设计上述加减速持续时间,通过上述滤波器对指令进行滤波后,机动的角度仍然为aΔt1Δt2,从而满足姿态机动的需求.
对于图2中的加速度段,机动角度的拉氏变换为

下面以(11)式中的结构滤波器为例,对滤波后的指令进行分析,则经过滤波后的姿态角为:


对上式求反拉式变换,则上述响应在宽度为Δt1的方波输入下,输出为:
θ1(t)=θf(s)-θf(s-Δt1)(15)
于是有


等稳定的极点都收敛后,该角度为:

在第一个方波输入延时Δt2后,加入反向的另一个方波,即减速段,则其响应角度为:
θss2(t)=θss1(t-Δt2)

上述两项相加,即得最终的机动角度:
θss(t) =θss1(t) +θss2(t) =aΔt1Δt2(19)
即通过上面的推导,可以看到,通过滤波后,要想使最终机动的角度还为aΔt1Δt2,需要满足的条件是上述θss1(t)、θss2(t)中的稳定极点项收敛到足够小,一般上述极点与挠性航天器的振动模态相关,其收敛时间在振动模态的周期的量级,比如对于0.1 Hz的振动模态,其收敛时间约10 s,对于更高频率,该收敛时间更短.因此通过本方法,可以保证在低频模态情况下,系统收敛时间保持在低水平.
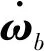
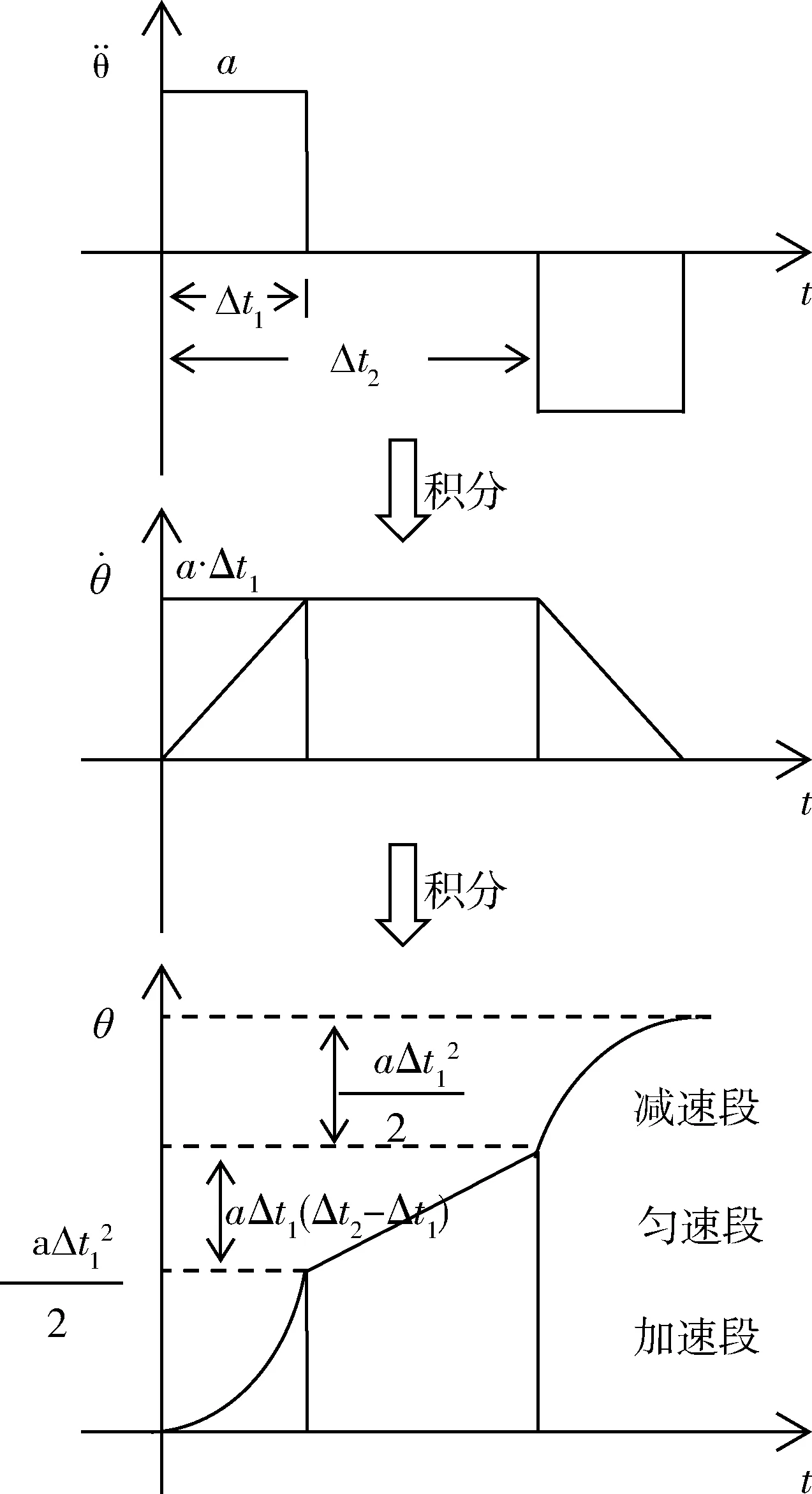
图2 Bang-Bang机动过程规划方案Fig.2 Attitude Maneuver with Bang-Bang Method
3 仿真验证
3.1 数学仿真
设某大型航天器星体转动惯量:
两翼帆板的频率为[0.318 0.92 1.728 1.883 4.83]Hz,其中第1阶和第2阶模态的耦合系数最大,是主要模态.本文考虑执行机构的响应能力设计一个惯性低通滤波器,并针对第1、2阶模态设计两个陷阱波器,取三轴机动指令滤波器形式如下:
其中,τ1=0.1,ξ1z=ξ2z=0.05,ξ1p=ξ2p=1.0,ω1z=ω1p=1.998 1,ω2z=ω2p=5.780 5.
滚动轴、俯仰轴分别需要进行20°、24°的姿态机动,机动角加速度最大值分别取0.025(°)/s2、0.03(°)/s2.仿真结果见图3~图13所示.通过图3、图4可以看到,进行滤波后,加速度指令相比Bang-Bang指令,波形上约有变化,在跳变处变得连续,从图5~图7可以看到,角速度的最大值变化并不大,但机动到位后,采用滤波算法,稳定的时间要远小于传统的Bang-Bang算法,Bang-Bang算法稳定时间超过了100 s,而采用滤波算法后,稳定的时间在几秒量级,不超过10 s.因此对振动的抑制效果非常显著.图8、图9分别为滚动轴、俯仰轴机动角速度曲线,两轴分别在Bang-Bang算法和本文滤波算法下,均机动到了期望角度;图10、图11分别为Bang-Bang算法和本文滤波算法中星体实际的控制力矩,可以看到,两者在幅值和波形上区别并不大,但结合上述分析,对星体角速度的稳定时间的影响却区别非常大;同样,还可以通过图12、图13对比Bang-Bang算法和本文滤波算法中挠性模态的振动情况,可以看到传统的Bang-Bang算法,挠性模态得到了很大的激励,是典型的二阶挠性模态的振动,但采用本文的滤波算法后,挠性模态只变形,基本上不振动,机动过程中处于一种近似静止的静态变形,其最大形变幅度与Bang-Bang算法在一个量级,但其振动幅度比Bang-Bang要小二个量级以上.

图3 滚动轴角加速度滤波前后对比图Fig.3 Angular Acceleration in Roll Axis
3.2 物理试验
本次试验采用单轴气浮台,转动惯量约为150 kg·m2左右.采用专门设计的挠性模拟板模拟卫星太阳翼的挠性特性.其尺寸为:3 700 mm×300 mm×5 mm,材料为钢.
本试验中,为了突出挠性附件的振动特性,在太阳翼模拟器的端部安装砝码,使其基频降低到0.1 Hz.针对该模态频率,设计如下滤波器:
其中,τ1=0.1,ξ1z=0.05,ξ1p=1.0,ω1z=ω1p=0.628 3.
图4 俯仰轴角加速度滤波前后对比图Fig.4 Angular Accelerations in Pitch Axis
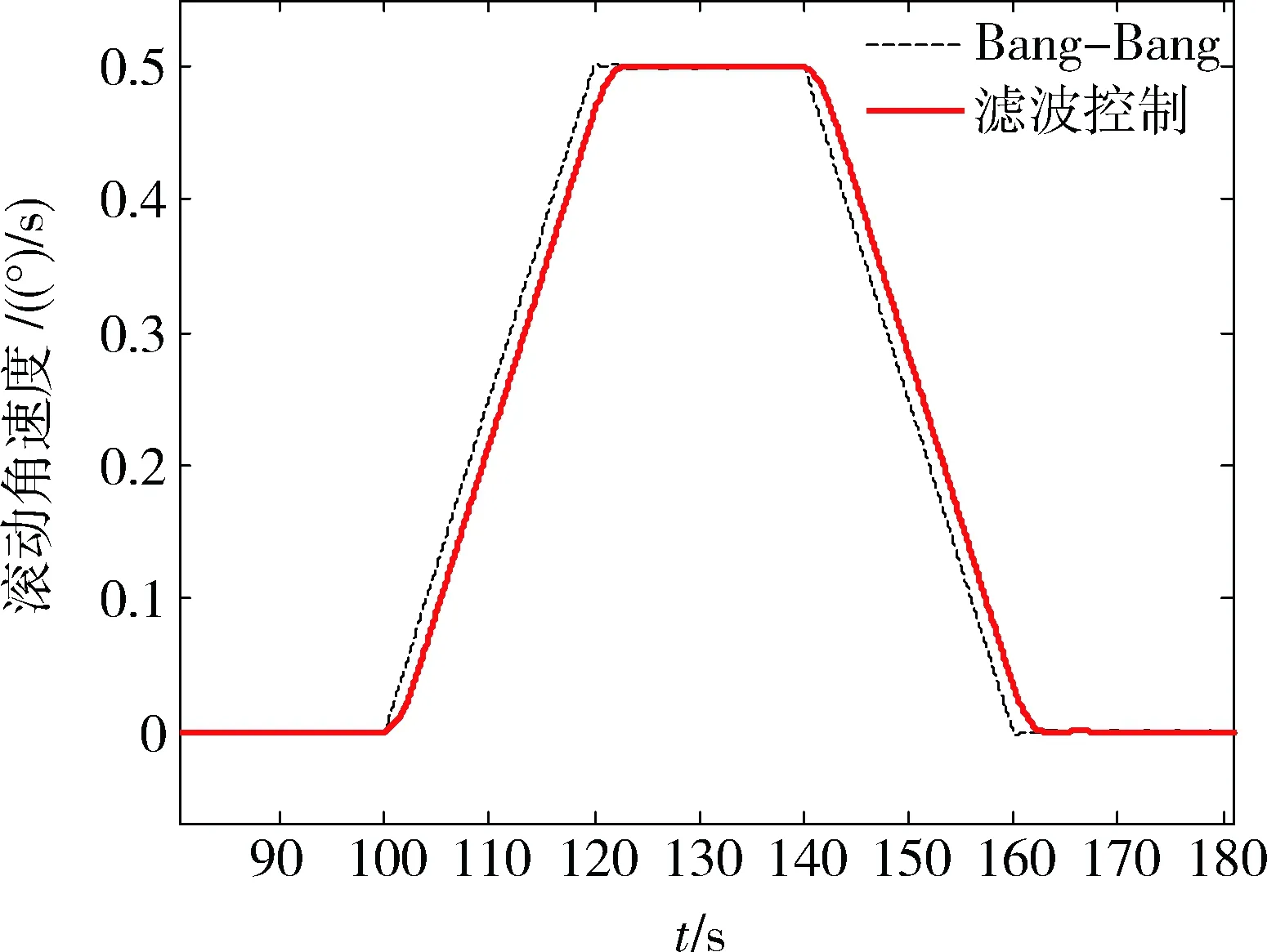
图5 滚动轴角速度滤波前后对比图Fig.5 Angular Velocities in Roll Axis
图6 滚动轴角速度滤波前后对比图(放大)Fig.6 Detailed Angular Accelerations in Roll Axis
图7 俯仰轴角速度滤波前后对比图(放大)Fig.7 Detailed Angular Accelerations in Pitch Axis

图8 滚动轴机动角度Fig.8 Angles in Roll Axis
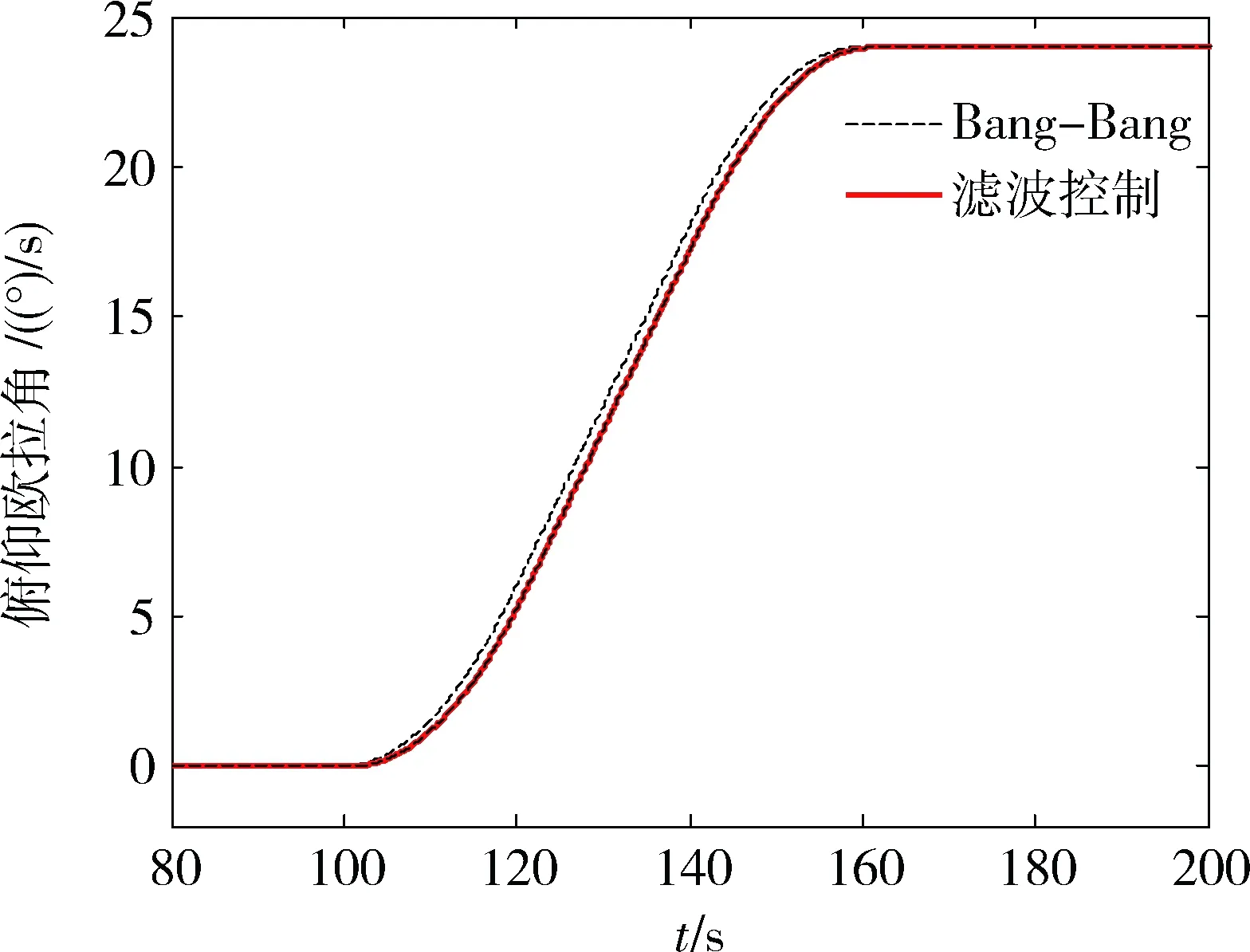
图9 俯仰轴机动角度Fig.9 Angles in Pitch Axis
采用滤波器方法时,进行了30°的机动,仿真结果可以看到,进行30°机动时,机动加稳定的时间不过40 s,采用本文中设计的滤波器方法后,稳定的时间小于10 s,整个系统机动和稳定的时间远小于项目预期指标.
而采用普通的Bang-Bang方法做机动时,挠性附件激起的振动持续时间达到近100 s.采用本文所用的滤波方法,将稳定时间降低了约90%.

图10 Bang-Bang指令下三轴控制力矩Fig.10 Control Torques in Bang-Bang Command

图11 滤波后三轴控制力矩Fig.11 Control Torques in Command Filter
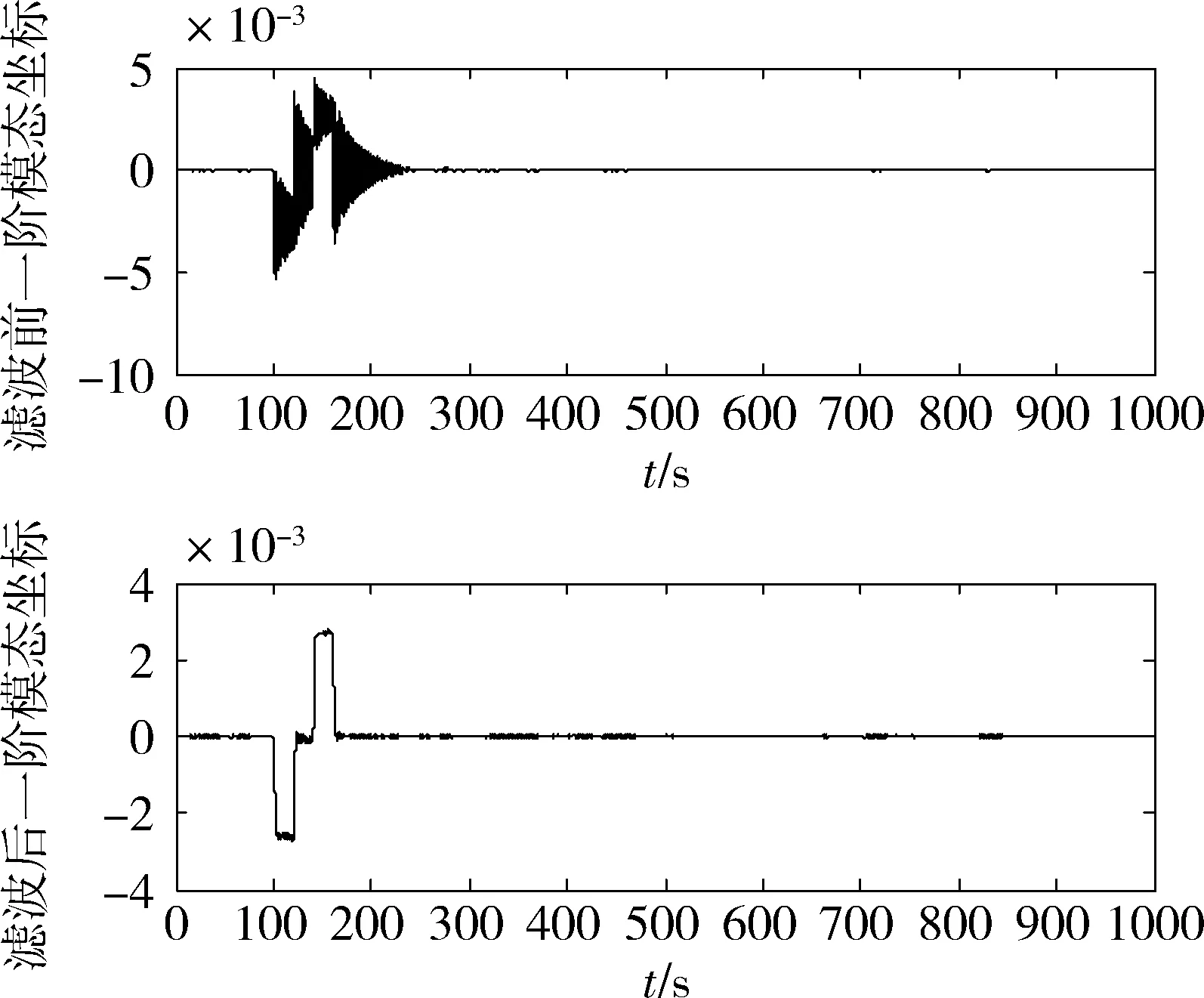
图12 滤波前后第一模态坐标对比图Fig.12 Vibration of First Mode

图13 滤波前后第二模态坐标对比图Fig.13 Vibration of Second Mode

图14 单轴气浮台照片Fig.14 Air Floating Test-bed in Single Axis

图15 平行构型安装的SGCMGFig.15 SGCMG in Parallel Configuration

图16 机动角度Fig.16 Maneuver Angles

图17 机动角度放大图Fig.17 Detailed Maneuver Angles

图18 机动角速度Fig.18 Maneuver Angular Velocities
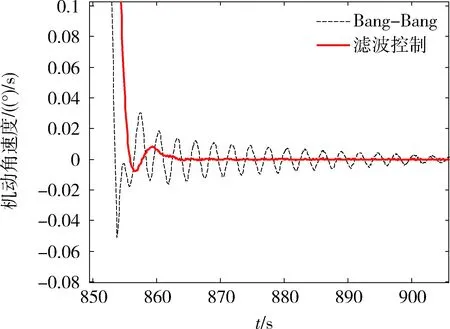
图19 机动角速度放大图Fig.19 Detailed Maneuver Angular Velocities
4 结 论
针对低频模态航天器的姿态机动控制,本文设计了基于滤波方法的机动路径规划,结合姿态跟踪控制器,实现了挠性航天器机动后的快速稳定控制.相对Bang-Bang及其它机动路径规划方法,本方法的特点是参数设计有依据,可针对具体航天器对象的挠性模态频率进行针对性设计,并且机动到位后稳定时间可预判,约为航天器主导挠性模态的振动周期.通过数学仿真和物理试验验证了方法的有效性和结论的正确性.
