ECMWF 细网格模式在北疆降雪预报中的统计检验

2019-07-20李健丽李博渊庄晓翠赵江伟

沙漠与绿洲气象 2019年3期

李健丽，李博渊，庄晓翠，赵江伟

（阿勒泰地区气象局，新疆阿勒泰836500）

目前，数值预报产品在内容、时效、层次上均不断增多，已成为预报员制作天气预报的主要参考依据[1]。正确理解其性能可以使预报人员有据可依，从而在预报工作中充分发挥人的主观能动性，取得较好的效果。然而，由于诸多原因数值模式的预报效果还不十分稳定，长时效数值预报产品与分析场或实况存在一定的误差。对预报业务或模式研发而言，全面了解模式的预报性能十分重要，一方面可检验模式性能在时空上的差异，向研发者反馈信息；另一方面，为预报员订正预报结果提供客观依据。因此，开展数值预报产品检验，无疑是一种了解模式性能行之有效的途径。

近年来，国家气象中心对T639、日本、ECMWF粗网格等数值模式的中期预报性能进行了定期检验和发布[2-5]，为预报员了解和掌握各家模式对中高纬环流形势、850 hPa 温度以及地面冷高压、西北太平洋副热带高压等重要天气系统的预报能力，提供了可靠的参考依据。然而，中国幅员辽阔，地形复杂，在制作当地要素预报时，既需要参考数值模式对环流形势和天气系统的预报，更需要参考数值模式的格点要素预报值。因此，数值模式的格点要素预报精度引起了各级预报员广泛而高度的关注，如许多学者对T639、EC 细网格模式在降水和温度预报[6-14]方面开展了大量的应用检验工作；庄晓翠等[15]对T639 数值预报产品在新疆北部暖区强降雪中的预报进行较详细的检验；相关研究为预报员更好地应用模式降水和温度预报以及新疆暖区强降雪预报提供借鉴。上述数值模式预报性能检验多是针对天气系统和天气现象的天气学检验，且时空分辨率有限，利用其制作精细降雪预报产品难度较大，要实现降雪的定点、定量、定时的短时预报预警难度更大。

2015 年1 月15 日EC 细网格模式升级后，在新疆预报业务中正式应用，部分产品空间分辨率提高到0.125°×0.125°，比先前的提高了2 倍，从而为天气预报提供了更精细的参考依据。本文主要运用统计学方法检验升级后EC 细网格模式形势场、物理量场及TP 降水量在北疆2015 年1 月—2017 年4月共20 场降雪天气中的预报能力，分析预报产品的统计误差及相关系数，为今后预报北疆短期降雪天气提供参考依据。

1 资料和方法

1.1 资料选取

图1 北疆地区地形及站点分布

研究区域为北疆地区（78°~92°E，42°~50°N），降雪实况选用该区域51 个发报站（图1）2015 年1 月15 日—2017 年4 月逐日降雪资料。降雪量级标准按气发〔2004〕45 号《新疆降水量级标准（修订版）》文件划分，即0.1~3.0 mm 为小雪，3.1~6.0 mm 为中雪、6.1~12.0 mm 为大雪、12.1~24.0 mm 为暴雪、24.1~48.0 mm 为大暴雪。本文按上述标准统计24 h（20~20 时）降雪量＞0.1 mm 降雪过程，满足日平均气温≤2 ℃的雨夹雪过程，也入选本研究个例，否则不入选，共有20 场小量以上降雪过程。

EC 细网格模式产品（分辨率）（简称EC 细）以起报时间为20 时和08 时为主；检验预报时效为12、24、36、48、60、72 h。由于北疆大部分测站拔海高度低于1500 m，因此，主要选取850~300 hPa 的物理量进行检验。

1.2 检验方法

定量检验（统计检验）采用世界气象组织（WMO）推荐的预报检验方案，用模式初始场的客观分析资料为实况，针对08 时和20 时起报的模式产品，分别对上述预报时效要素场进行检验。选用平均误差ME、均方根误差RMSE、平均绝对误差MAE、相关系数R[16-17]4 种统计量对EC 细网格模式产品进行统计检验。根据有关文献[17-18]可知，平均误差、平均绝对误差、均方根误差分别在±1.5 个单位内及＜3、＜4.5 个单位，为较小，反之较大。相关系数为＞0.60 时模式具有一定的参考价值，反之，相关性较小，基本无参考价值。

EC 细网格模式降水预报产品选用累计降水量TP（简称EC 细降水预报），以起报时间为20 时和08 时为主；检验预报时效为12～24 h、24～36 h、36～48 h、48～60 h、60～72 h 共5 个时效段的12 h 累计降水预报产品。首先对EC 细降水预报产品，运用双线性插值法[16]将模式格点降水量插值到站点上，再与对应站点的实测降水量进行对比检验，分别对上述预报时效段的12 h 降水量进行检验。选用平均误差、均方根误差、平均绝对误差3 种统计量进行检验；并运用中国气象局《中短期天气预报质量检验方法》分别对EC 细网格模式TP 降水量产品的12 h累积降水预报进行预报准确率、空报率、漏报率的检验评估。

2 检验结果分析

2.1 形势场

对于降雪的短时和短期预报，预报员一般是在天气形势分析的基础上，结合物理量参数进行预报区域上空大气温湿结构的综合分析，从而判断是否有降雪天气发生，以及发生的时间段和强度。天气变化是天气形势或大气环流演变的结果，模式对形势场的预报准确与否，直接关系到近地面要素预报准确率，所以对形势场的预报检验就显得尤为重要。

通过计算北疆区域内20 场降雪过程的ECMWF 细网格模式500 hPa 高度场（单位为dagpm）、850 hPa 温度场（单位为℃）及海平面气压场（单位为hPa）（简称形势场）的4 种检验统计量，可知（图2），500 hPa 高度场误差在0 dagpm 附近，最大为0.13 dagpm，48 h 时效内＜0.06 dagpm；850 hPa 温度场平均误差0～0.45 ℃，表明预报比实况略偏大；海平面气压场平均误差＞-1.28 hPa，比实况偏小（图2a）。形势场的平均绝对误差均为0.290～1.717，48 h 内＜1.27（图2b），均方根误差为0.350～2.006，48 h 内＜1.49（图2c），均是500 hPa 高度场的误差最小。3 类误差除500 hPa 高度场的平均误差外，在数值上随时效的延长略有增大（图2）。从起报时间来看，08 时起报的误差略＞20 时。可见，EC 细网格模式对形势场预报误差小，精度高。由图2 d 可知，该模式对形势场预报的相关性较高，72 h 预报时效内均高于0.95。

2.2 物理量场

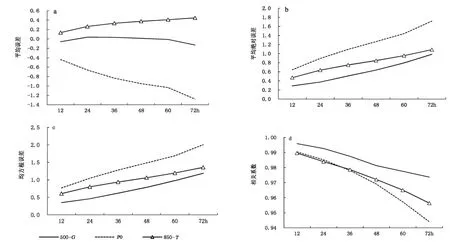
图2 EC 细网格模式对形势场预报的平均误差（a）、平均绝对误差（b）、均方根误差（c）及相关系数（d）随时效的演变

要了解EC 细网格模式对降雪的预报性能，不仅要求形势场预报十分准确，物理量的预报准确与否也十分必要。因此，开展对该模式物理量场的检验，可以从多角度、多层面了解模式，方便模式研发者对其进行改进；同时为预报业务提供参考依据。

2.2.1 水汽条件

运用同样的方法计算ECMWF 细网格模式中850 hPa 比湿（单位：g·kg-1）、对流层相对湿度（单位：%）的4 种统计检验量，得到对水汽场72 h 预报时效内的检验（图3），平均误差的绝对值均＜2.09，48 h 时效内＜1.64，其中，850 hPa 比湿误差最小，在0 g·kg-1附近，700 hPa 相对湿度误差最大；对流层中低层相对湿度比实况偏小，且偏小的程度随时效增加而增大（图3a）。850 hPa 比湿的平均绝对和均方根误差分别为0.092~0.255、0.135~0.364 g·kg-1，对流层中低层相对湿度分别为3.818~16.93、5.495%~23.626%；850 hPa 比湿随时效变化不大，相对湿度随时效增大（图3）。分析表明，850 hPa 比湿的误差较小，对流层中低层相对湿度较大。该模式水汽场与实况的相关性72 h 时效内均＞0.60,48 h 内＞0.73，随时效减小（图3d）。从不同起报时间来看，850 hPa 比湿和500 hPa 相对湿度08 时起报误差略＜20 时，而对流层低层相对湿度则相反。可见，850 hPa 比湿在降雪预报中具有较好的参考价值，对流层中低层相对湿度随机误差大，在预报业务中需订正运用。

2.2.2 热动力条件

热动力条件是降雪的必要条件之一，因此，预报的准确与否至关重要。72 h 预报时效内对流层中低层垂直速度和对流层位涡平均误差均较小，绝对值＜0.10；60 h 时效内850 hPa 垂直速度和700 hPa位涡预报比实况略偏小，其它略偏大，300 hPa 位涡随时效增大，其它变化规律不明显（图4a）。垂直速度的平均绝对误差比位涡大，位涡为0.227×106~0.739×106，而垂直速度为1.642~3.034×106Pa·s-1，48 h 时效内＜2.83×106Pa·s-1（图4b）。均方根误差相对较大，300 hPa 位涡最小（0.339~0.965 106），700 hPa位涡和对流层中低层垂直速度为1.665~4.701，48 h预报时效内均＜4.46（图4c）。500 hPa 垂直速度72 h时效及300 hPa 位涡60 h 和72 h 时效的相关系数＜0.60，其它热动力条件均＞0.60，48 h 时效内＞0.62（图4d）。从不同起报时间来看，对流层中低层垂直速度是08 时起报误差比20 时略小；700 hPa 位涡20时起报误差比08 时略小，300 hPa 位涡2 个起报时次基本一致。由此可见，EC 细网格模式48 h 预报时效内对垂直速度和位涡的预报精度较高，尤其是位涡。

图3 EC 细网格模式对水汽场预报的平均误差（a）、平均绝对误差（b）、均方根误差（c）及相关系数（d）的演变

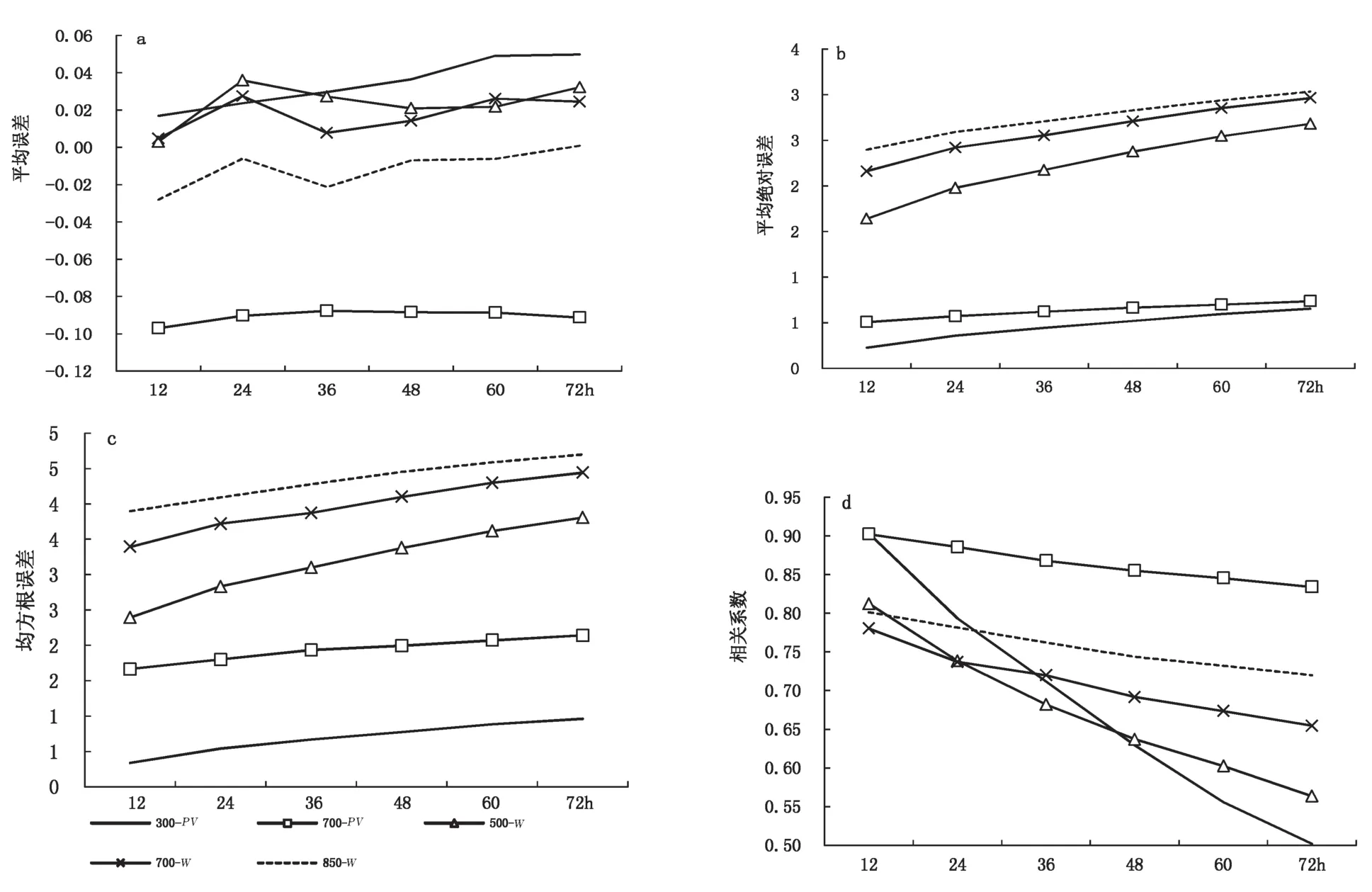
图4 EC 细网格模式对热动力场预报的平均误差（a）、平均绝对误差（b）、均方根误差（c）及相关系数（d）随时效的演变

另外，该模式对对流层低层散度预报72 h 时效内，平均误差为＜0.50×10-5s-1，平均绝对误差和均方根误差为27.404×10-5~82.236×10-5s-1，相关系数48 h 时效内＞0.63。可见散度场的系统性误差较小，随机误差较大[15-16]，在预报工作中需注意。

2.2.3 u、v 风场

风场在降雪预报中有着不可低估的作用，如高低空急流、垂直风切变、切变线、辐合线等，因此，EC 细网格模式对对流层u、v 风场的预报检验就显得尤为重要。就72 h 预报时效内而言，平均误差的绝对值＜0.16 m·s-1（图5a）；平均绝对误差为0.530~4.344 m·s-1，48 h 预报时效内＜3.20 m·s-1（图5b）；均方根误差为0.768~5.535 m·s-1，48 h 内＜4.13 m·s-1（图5c）。3 类误差850 hPa v 风场最小，平均绝对和均方根误差随时效增大（图5b、5c）。对流层风场预报的相关系数均＞0.75，48 h 预报时效内＞0.84，随时效减小（图5d）。说明EC 细网格模式对对流层u、v 风场的预报精度较高，有一定的参考价值。从不同起报时间来看，850 hPa u、v 风场20 时起报的误差略＜08 时，而700 hPa和300 hPa u、v 风场是08时起报的误差略＜20 时。

综上所述，EC 细网格模式对形势场、850 hPa比湿和u 风场、对流层位涡、对流层低层v 风场平均误差和均方根误差均较小，尤其是48 h 预报时效内。对流层中低层相对湿度平均误差较小，且表现为一致的负值，表明预报比实况偏小；均方根误差较大，表明相对湿度主要以非系统性的随机误差为主[16-17]。对流层低层散度、对流层中低层垂直速度、300 和700 hPa u 风场及300 hPa v 风场平均误差都很小，且没有明显的正值或负值偏差，说明系统误差不明显；而均方根误差较大，尤其是对流层低层散度，说明这些物理的随机误差较大，尤其是散度[15-16]。

3 EC 细网格模式在北疆降雪中的应用模型

通过上述分析，基于降雪的预报思路，总结出EC 细网格模式48 h 时效内在北疆降雪中的应用模型（图6）。模式对海平面气压场、850 hPa 温度场、500 hPa 高度场的大尺度环流形势预报精度较高，在预报业务中具有较高的参考价值。对850 hPa 比湿及对流层低层u、v 风场和高空位涡的预报误差较小，为首选物理量；对流层中低层相对湿度、垂直速度及高空u、v 风场的随机误差较大，在预报中注意订正应用。

4 降雪落区的检验

关于EC 细网格模式降水预报产品在新疆北部降雪预报的应用，张俊兰等[11]、李博渊等[19]对降雪天气的预报准确率、空报率和漏报率、统计误差等已做了较详细的检验，因此，本文选取2015 年以来5 次新疆北部暖区降雪天过程（以下简称降雪）进行检验。

图5 EC 细网格模式对风场预报的平均误差（a）平均绝对误差（b）均方根误差（c）及相关系数（d）不同时效变化曲线

图6 EC 细网格模式在北疆降雪预报中的应用模型

4.1 准确率评估

由图7 可知，就平均而言，EC 细网格模式TP 降水预报产品在新疆北部暖区降雪天气预报中小雪的准确率（即TS 评分）最大，暴雪最小（图7a）。72 h 预报时效内，模式对该区小雪的预报准确率为28.3%~38.5%，12~36 h 内和48~72 h 时效内TS 随时效的延长而增大，36~48 h 内则减小，最大出现在24~36 h 时段内（35.8%）。中雪预报准确率明显小于小雪，为13.3%~21.7%，随时效TS 评分基本以增大为主。大雪和暴雪12~48 h 内随时效的延长减小，之后则增大，最大TS 出现在60~72 h 时效（26.9%和20.0%）（图7a）。可见，各级降雪量随时效的延长其预报准确率并非减小，尤其是中雪。

由图7b 可知，小雪的空报率最大（47.1%~51.9%），暴雪最小（10%~30.8%）。大雪和暴雪48 h之后，空报率随时减小，之前没有明显的规律；中雪空报率随时效基本以减小为主，小雪变化较小。平均而言，暴雪的漏报率最大，达61.5%~72.7%，随时效变化是48 h 之前较小，之后先增大再减小；大雪次之（36.6%~57.6%），72 h 呈抛物线性变化；中雪的漏报率为37.3%~44.6%，24 h 内随时效呈增大的趋势，之后呈减小的趋势；小雪的漏报率最小（12.3%~24.2%），随时效没有明显的规律（图7c）。可见，72 h预报时效内，小雪的空报率明显高于漏报率，中雪和大雪的空报率和漏报率基本相当，而暴雪漏报率明显高于空报率。

4.2 误差评估

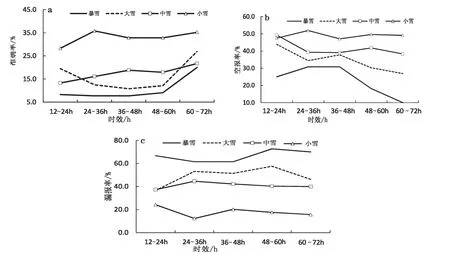
图7 EC 细网格模式TP 产品对北疆冬季各级降雪量的预报能力检验及不同时效变化曲线

就区域平均而言（图8a），EC 细网格模式降水预报产品72 h 预报时效内的5 个降水时段的平均误差为-0.712~0.017 mm，表明存在负的系统性误差，即预报比实况值偏小，24 h 之后随时效的延长呈增大趋势；平均绝对误差和均方根误差分别为2.656~2.939 mm、3.610~4.165 mm，随时效变化较小。说明EC 细网格模式降水预报产品在新疆北部暖区降雪预报中系统误差较小，随机误差较大。总体来说，72 h 预报时效内EC 细降水预报产品在暖区降雪中预报中误差相对较小具有较高的参考价值。

由于目前国家气象局对降雪量的评分是将12 h 累积降雪量分为小雪、中雪、大雪、暴雪进行，那么在实际预报业务中预报员就高度关注模式对各级降雪量的预报误差。因此，有必要对各级降雪量的误差进行分析，以便为预报员在制作降雪量级预报时提供客观依据。EC 细网格模式降水量平均误差暴雪最大（-9.082~-12.141 mm），随时效规律性不大；大雪次之（-3.310～-4.558 mm），中雪最小（-0.116～-1.074 mm），小雪也较小（1.190～1.720 mm）（图8b）；因此，小雪的预报值比实况偏大，其它各级降雪的预报值均以偏小为主；大、中、小雪随时效变化较小（图8b）。平均绝对和均方根误差均是暴雪的最大（8.53～14.374 mm），随时效呈减小—增大—减小的变化趋势，最大误差出现在48~60 h，最小出现在24~36 h；大雪次之（3.925～6.015 mm），呈抛物线型，最大也出现48~60 h，最小出现在60~72 h；中雪为（2.462～3.743 mm），随时效变化不大；小雪为（1.419～3.025 mm），随时效变化不大（图8c、d）。

由此可见，小雪和中雪的3 种误差均较小，随时效的延长变化较小，说明模式对12 h 累计降雪量为小雪和中雪的预报相对较稳定；而强降雪的误差较大，随时效的延长并非呈增大的趋势，这与文献[18]随时增大有所不同。