多级组合型大角度变幅机构的动力学特性
2019-07-20朱振新朱建新唐博豪顾林坤钱奂云
朱振新,朱建新,,唐博豪,顾林坤,钱奂云
(1.中南大学 高性能复杂制造国家重点试验室,湖南 长沙,410083;2.山河智能装备股份有限公司国家级企业技术中心,湖南 长沙,410100)
桩架是一种广泛使用的桩工机械,可搭载振动锤、液压锤、螺旋钻机、深层搅拌机、套管驱动机等多种工作装置实现多工法、多桩型施工,具有一机多用、地质适应性强的特点。桩架主要由行走底盘、回转平台、桅杆、变幅机构组成[1],变幅机构主要起变幅和支撑作用,在变幅时起架桅杆,在施工时传递载荷,是保证整机稳定性与施工质量的关键部件。桩架的变幅机构有2种基本构型:一种由单组液压缸、桅杆和机身铰接成三点式结构的单级变幅机构,利用液压缸的伸缩实现桅杆变幅,其实质为四杆机构中的摇块机构或导杆机构,这种变幅机构结构简单,但因为桩架平台和液压缸尺寸的限制,其变幅范围有限,若要增大变幅角度,则三点式结构中的上铰点必须移至桅杆中下部,这将导致整机稳定性较差;另一种为三点式结构串联平行四边形结构,该机构可通过下部液压缸的伸缩实现桅杆平动,可增加桩架工作半径,方便钻孔时对桩位中心,但该种机构仍然是通过三点式结构的单级变幅机构实现桅杆变幅,而且结构较为复杂,机构中各铰点均位于机器前部,变幅稳定性较差。目前,人们对桩架变幅机构的研究多集中于参数优化[2-6]、部件强度[7-8]、整机稳定性[9-11]、机液一体化建模[3,12]、油缸负载特性[13-15]等方面,相关研究都是针对2种传统变幅机构进行,研究对象具有高度相似性,且均是采用牛顿欧拉法或键合图法建立变幅机构的动力学模型。对于多个刚体组成的复杂机构,采用此方法不但可以求出主动力,而且可以计算出各约束反力,但随着刚体数目的增加,将涉及大量约束反力,使得计算效率低下。对于多级组合型变幅机构的动力学建模尤其是重点研究变幅机构主动力的情况,采用达朗贝尔-拉格朗日法[16-18]更为合适。此外,对于变幅机构的动力学特性研究,因为单级变幅机构变幅方式单一,所以,当前多是研究钻进工况下外部载荷变化对变幅机构的力学影响,而对变幅机构进行整体建模、仿真与试验的研究很少,针对不同变幅方式的动力学特性的研究则更少。为此,本文作者基于自主研发的多级组合型大角度变幅机构[19-20],建立该机构变幅过程的动力学数学模型,研究不同变幅方式下变幅机构的动力学特性,最后用试验验证模型及仿真结果的正确性。
1 机构原理的分析
2 种传统变幅机构示意图如图1所示。多级组合型大角度变幅机构如图2所示,主要构件包括桅杆、前液压缸、变幅架、后液压缸。该机构属于平面多闭链机构,由2 个四杆机构串联组合而成,其中,AECB闭链为导杆机构,CDE闭链为摇块机构。根据杆组拆分原理,部件1和部件2、部件3和部件4 均为Ⅱ级一缸杆组。该机构的自由度为2,主动副数为2 个,分别为前液压缸移动副和后液压缸移动副。通过前、后液压缸的伸缩,分别驱动导杆机构和摇块机构两级变幅,最终实现桅杆的大角度变幅。该结构相对现有变幅机构具有运动时所占空间小、传动角更优、变幅角度大的优势。
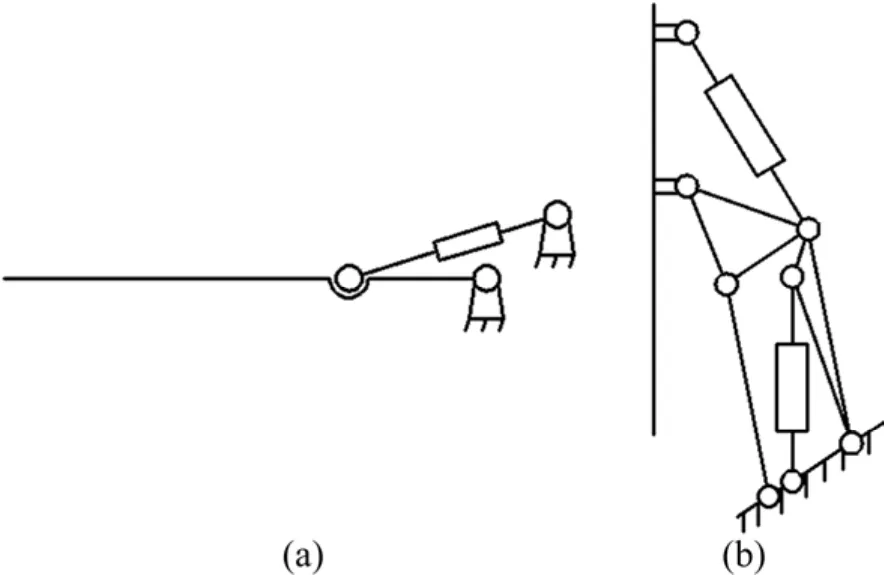
图1 2 种传统变幅机构示意图Fig.1 Schematic diagrams of two kinds of luffing mechanism
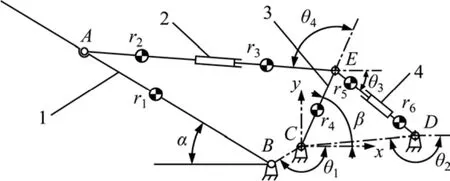
图2 多级组合型大角度变幅机构示意图Fig.2 Schematic diagram of multi-stage combined type large angle luffing mechanism
根据两级变幅的先后顺序和实际操作应用,变幅方式分为2 种:变幅方式1,后液压缸收缩达到极限位置,前液压缸再收缩,使得桅杆变幅达到垂直状态;变幅方式2,前液压缸收缩达到极限位置,后液压缸再收缩,使得桅杆变幅达到垂直状态。桅杆变幅是桩架作业工序当中非常重要的环节,其动力学性能直接影响变幅过程的稳定性和安全性。变幅机构的结构和变幅方式不同,其动力学性能则不同,因此,有必要进行深入分析与研究。
2 数学模型的建立
首先,求出该变幅机构的位置正解和位置反解方程,并以此为基础,采用层次化的求解方法[21],求出该机构的一阶速度雅可比矩阵和二阶加速度海森矩阵;然后利用简化动力学模型理论[16]。将该变幅机构分成3 个子机构,求出每个子系统的拉格朗日方程;最后,利用达朗贝尔原理和虚功原理整合各个子机构的动力学方程,推导出基于变幅机构前液压缸和后液压缸载荷的标准形式拉格朗日动力学方程[17-18]。
2.1 运动学建模
2.1.1 位置正解
位置正解方程就是根据前液压缸输入长度d1和后液压缸输入长度d2,求解桅杆与水平方向的夹角α、变幅架与水平方向的夹角β。以C点为坐标系原点,A点和E点可以分别表示为:
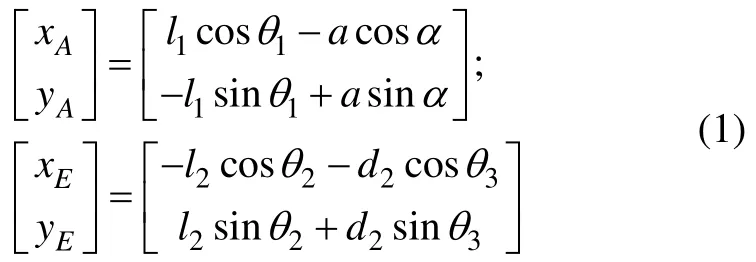
利用式(1)和余弦定理,可求解出对应桅杆转角的输出。
2.1.2 位置反解
根据桅杆与水平方向的夹角α、变幅架与水平方向的夹角β,计算前液压缸输入长度d1和后液压缸输入长度d2:
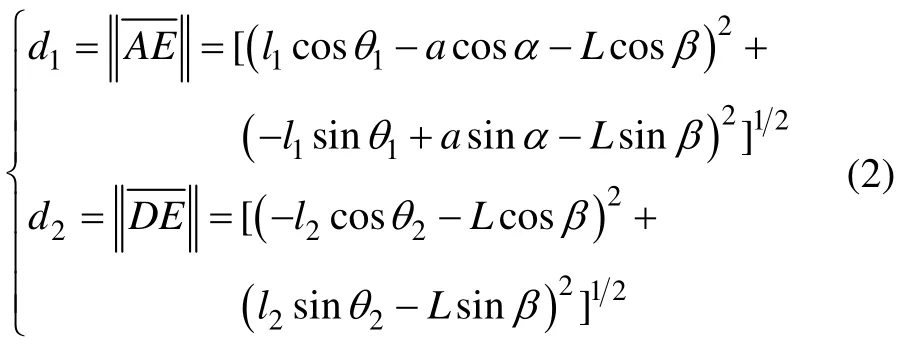
2.1.3 雅可比矩阵
一阶速度雅可比矩阵J表示的是输入速度矢量与输出速度矢量的映射关系。将d1和d2对时间直接求导较为困难,利用层次化的方法求解,先求解与的关系,再推导出与和的关系:
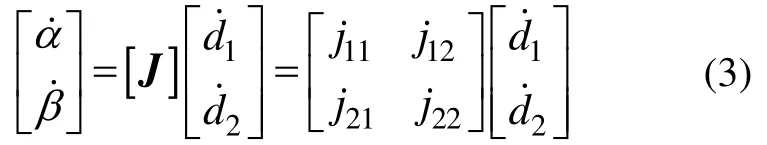
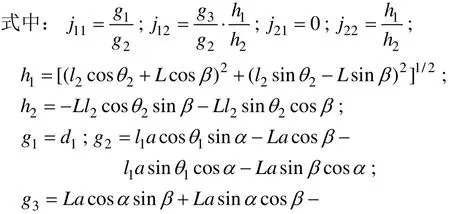
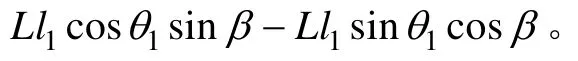
2.1.4 海森矩阵
二阶加速度海森矩阵H表示的是加速度的输入以及输出的映射关系。由于对一阶雅可比矩阵求导十分困难,因此也采用层次化的方法求解,先求解与的关系,再推导出与和的关系:
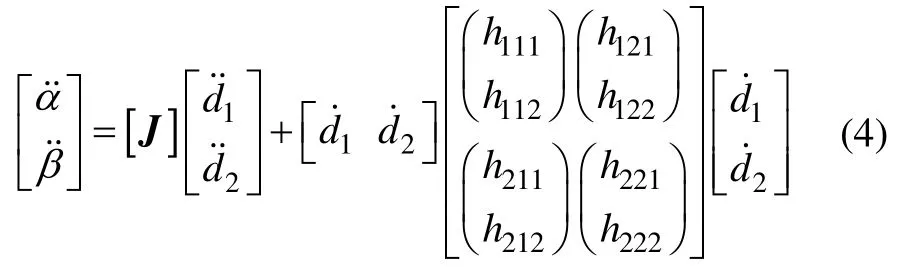
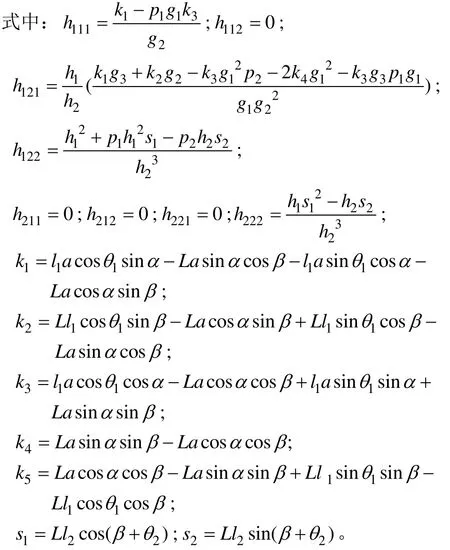
2.2 动力学建模
2.2.1 子模块力学模型的建立
拆分模块示意图如图3所示。该机构分成3 个子模块:模块Ⅰ为由桅杆与机身固定铰点组成的子模块;模块Ⅱ为由变幅架与前液压缸串联而成的子模块;模块Ⅲ为由后液压缸和机身固定铰点组成的子模块。
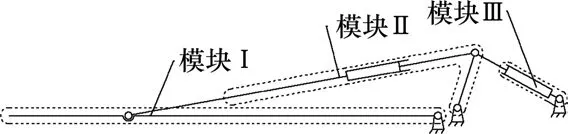
图3 拆分模块示意图Fig.3 Schematic diagram of split module
为便于动力学方程的建立,定义广义坐标为q=[αβ]T。模块Ⅰ的局部广义坐标可以直接利用α来表示,模块Ⅱ的局部广义坐标可以利用β,模块Ⅲ可与模块Ⅱ形成单自由度闭链机构。实际变幅工况下,液压缸负载很大且运行速度很慢,各杆件基本处于受拉状态,运动副摩擦、杆件柔性等因素对变幅机构主动力的影响很小,因此,动力学建模中忽略各运动副的摩擦,所有构件均视为刚体。
模块Ⅰ为单自由度机构,其局部广义坐标与全局广义坐标相同为q=[αβ]T。将模块Ⅰ动能势能求出后代入拉格朗日方程基本表达式,整理后得到其动力学方程:
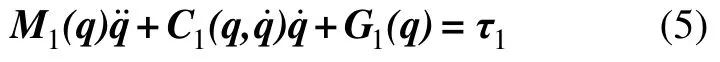
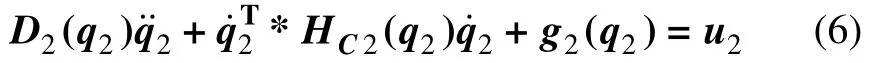
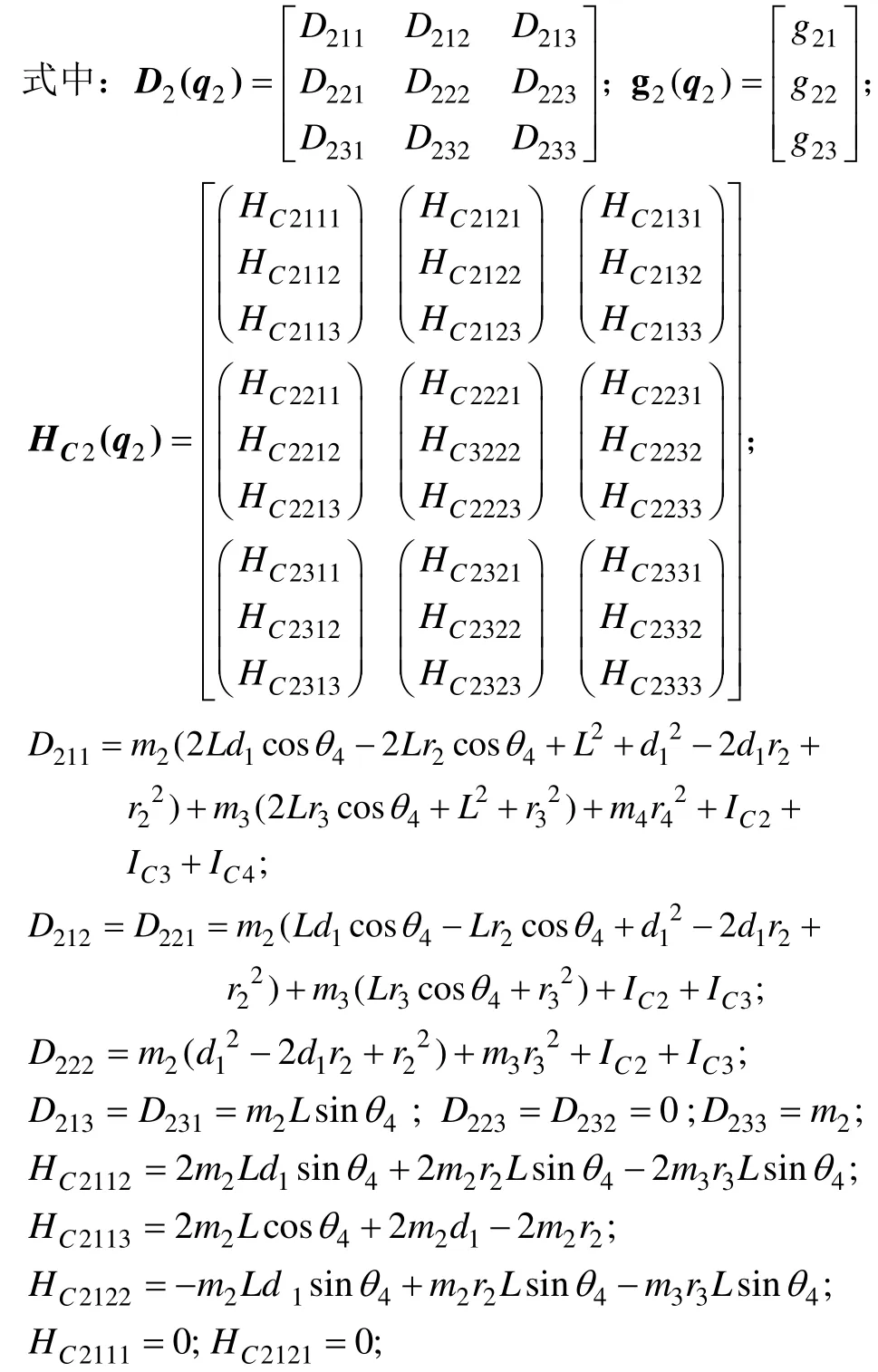
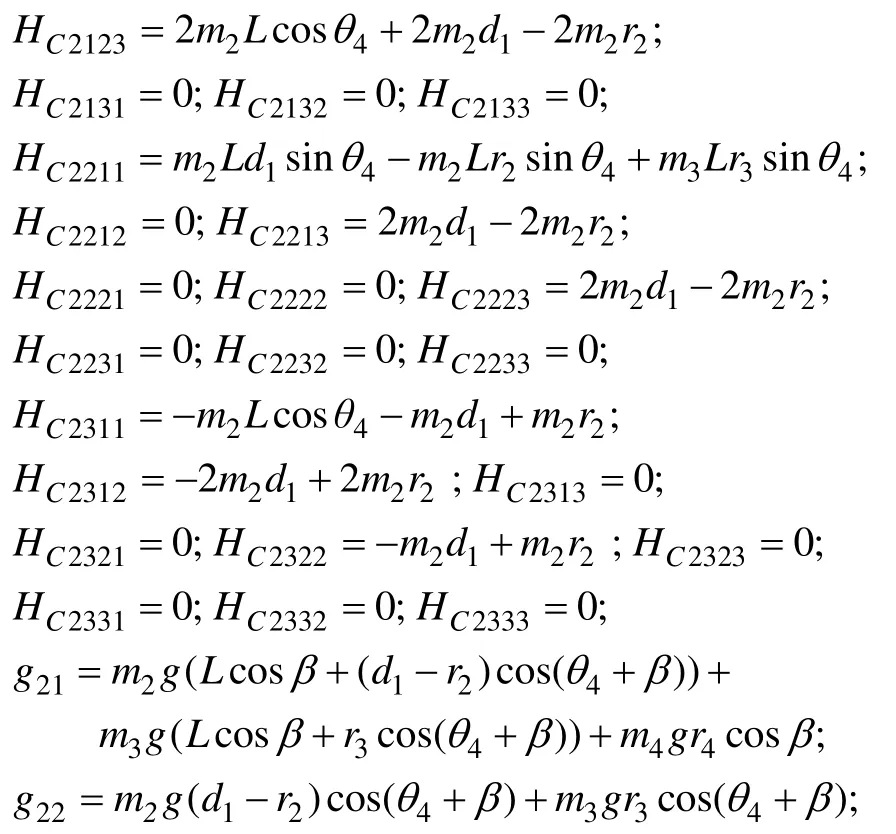
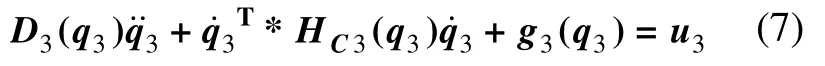

2.2.2 局部坐标与广义坐标的运动学关系
模块Ⅱ局部广义坐标与全局广义坐标之间的速度转换关系满足:
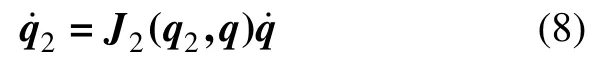
利用闭链AECB,对模块Ⅰ和模块Ⅱ中的A点表达式求导,联立便可解得
由式(8)对时间求导并代入式(9)得:
式中:H2(q2,q)为模块Ⅱ的局部广义坐标与全局广义坐标之间的加速度海森矩阵,

对于模块Ⅲ,同理可得:

解得
由式(11)对时间求导并代入式(12)得
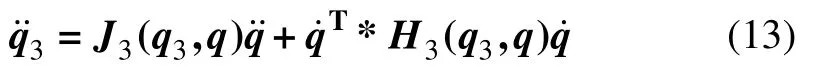
式中:H3(q3,q)为模块Ⅲ的局部广义坐标与全局广义坐标之间的加速度海森矩阵。
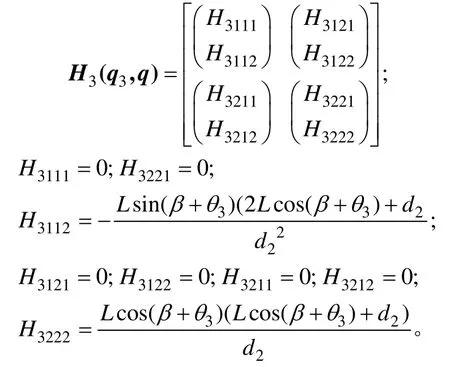
2.2.3 全局广义坐标下动力学模型的创建
结合虚功原理,作用到局部广义坐标上的广义力可以投射到全局广义坐标上。将式(6)左乘并代入式(8)和式(10),整理即可得模块Ⅱ在全局广义坐标上的动力学方程:
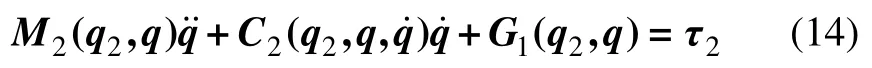
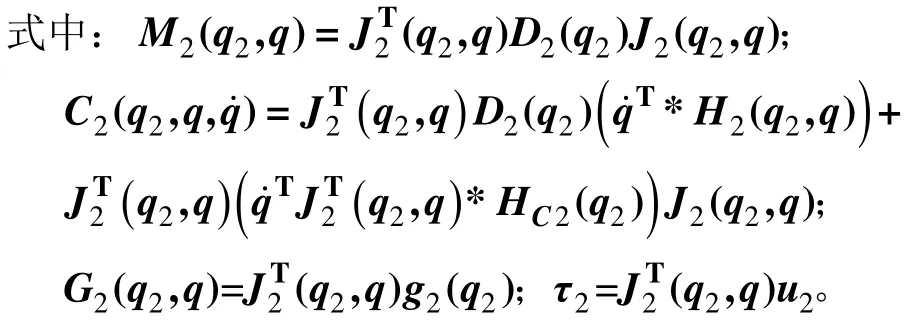
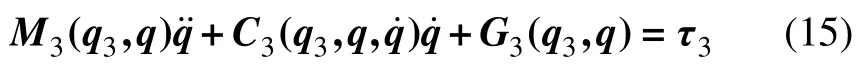
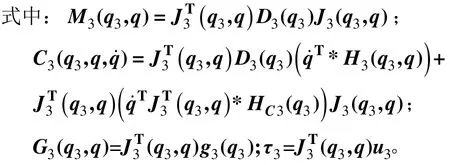
式(5),(14)和(15)相加即可得到全局广义坐标q=[αβ]T下的动力学方程:
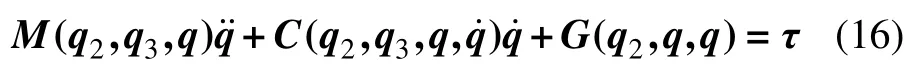
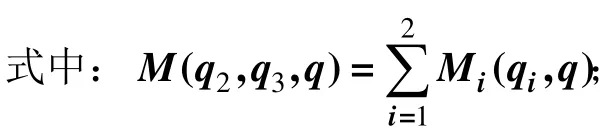
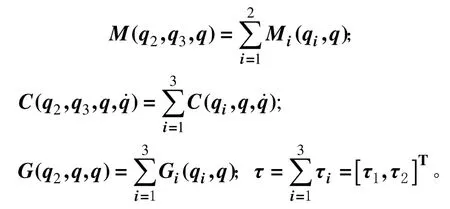
全局广义坐标q=[αβ]T与主动副d=[d1d2]T之间的一阶速度映射关系与二阶加速度映射关系如式(3)和式(4)所示,将其简单表示如下:
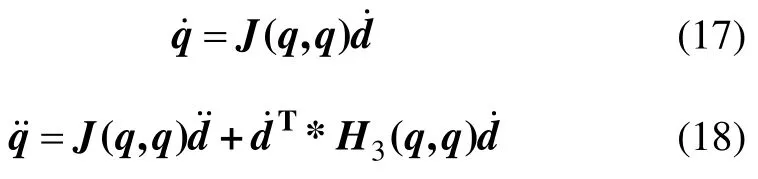
将式(16)左乘JT(q,q)并代入式(17)和式(18),整理得到多级组合型大角度变幅机构关于主动副的标准形式拉格朗日动力学方程:
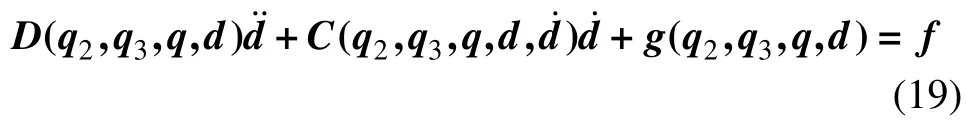
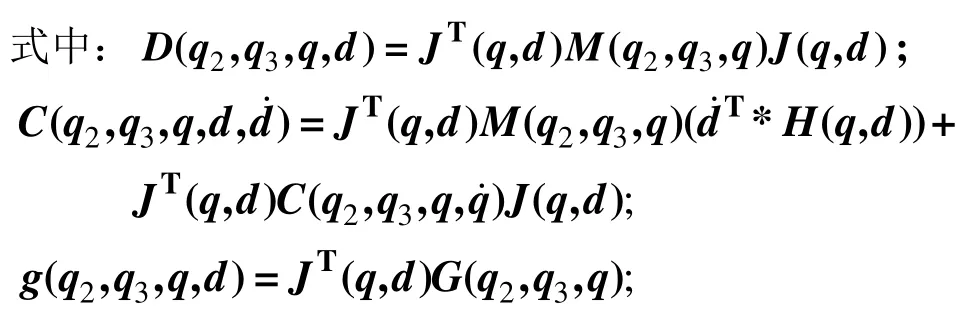
3 仿真分析
3.1 仿真模型的建立
多级组合型大角度变幅机构中各个构件的基本参数如表1所示,a=16 800 mm,L=3 054 mm,l1=1 315.68 mm,l2=5 622.81 mm,θ1=174.83°,θ2=158.60°,桅杆初始角度α=0°,变幅架初始角度β=67°。
设定前液压缸匀速运动时的速度v1=0.046 8 m/s,后液压缸为v1=0.042 6 m/s,只有在液压缸的启动和制动过程中存在变速运动,前后液压缸位移函数如下。以前液压缸和后液压缸的加速度、速度、位移为输入,基于前述动力学方程利用MATLAB 函数编写程序,便能仿真分析得到前液压缸和后液压缸在变幅过程中的载荷变化情况。
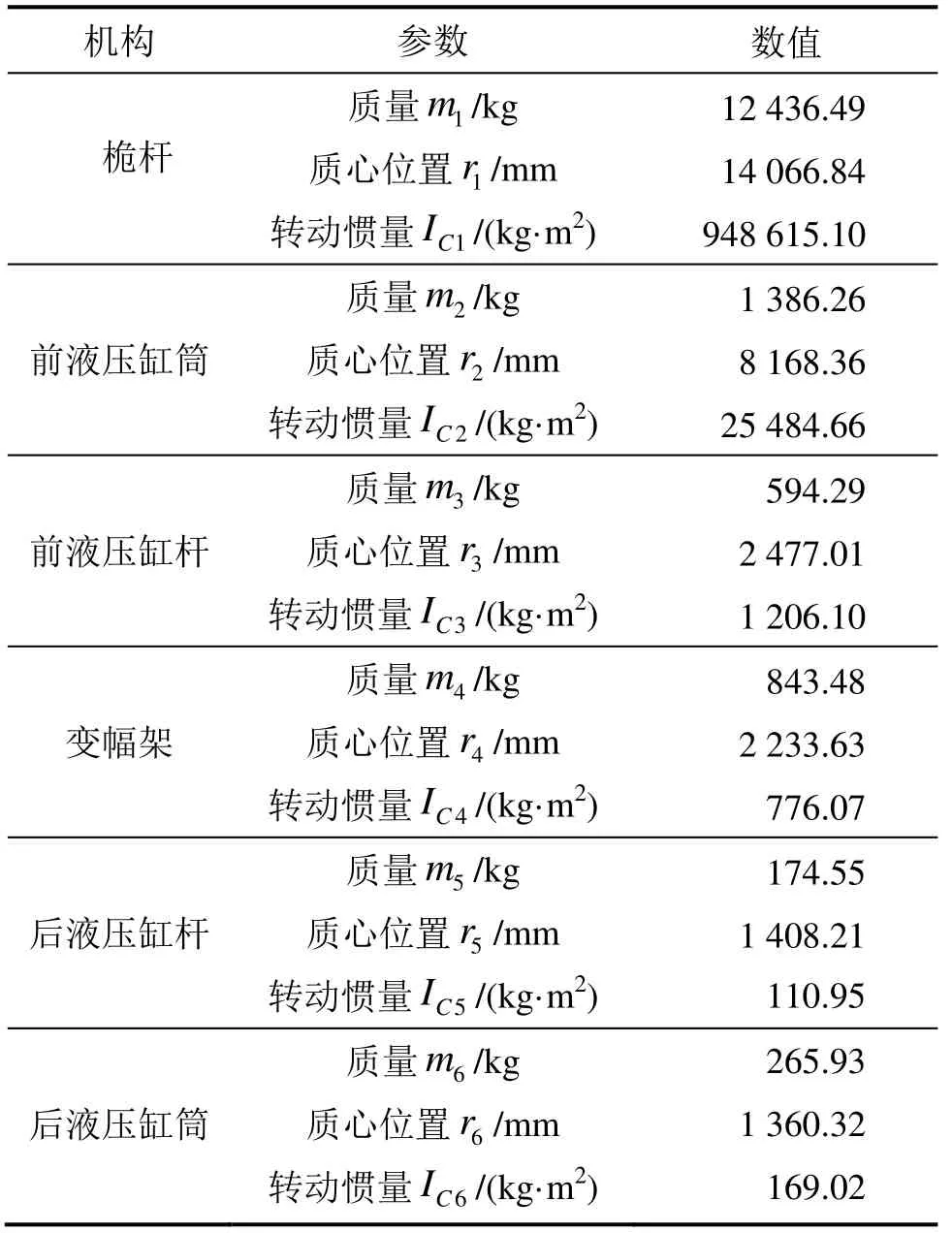
表1 变幅机构基本参数Table 1 Main parameters of luffing mechanism
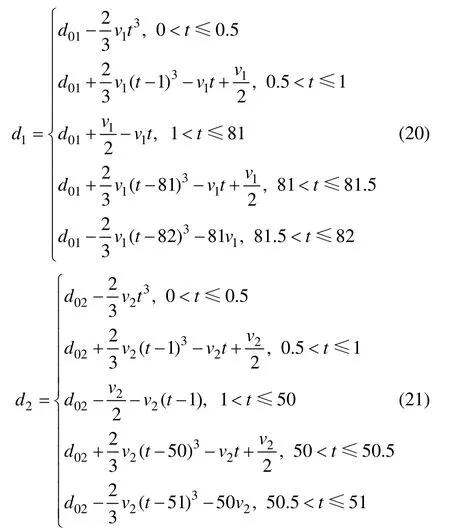
式中:d01为前液压缸伸出时的最大长度;d02为后液压缸伸出时的最大长度。
3.2 仿真结果分析
前液压缸和后液压缸在变幅过程中的载荷仿真曲线如图4和图5所示,图中,桅杆角度即为桅杆与水平方向的夹角α。由图4和图5可知:在2 种变幅方式下,前液压缸载荷和后液压缸载荷在桅杆角度分别为0°和90°时均相同。说明前液压缸、后液压缸的静载荷只与桅杆的姿态有关,与液压缸动作顺序无关;当桅杆角度为35°和58°时,因为前液压缸和后液压缸的启停,所以液压缸载荷出现突变冲击,符合实际变幅过程中液压缸启停时液压系统产生载荷冲击的情况。
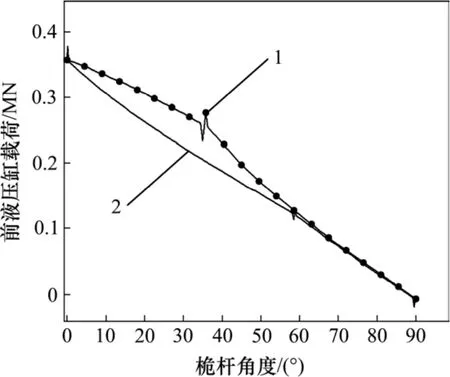
图4 前液压缸载荷Fig.4 Front hydraulic cylinder load
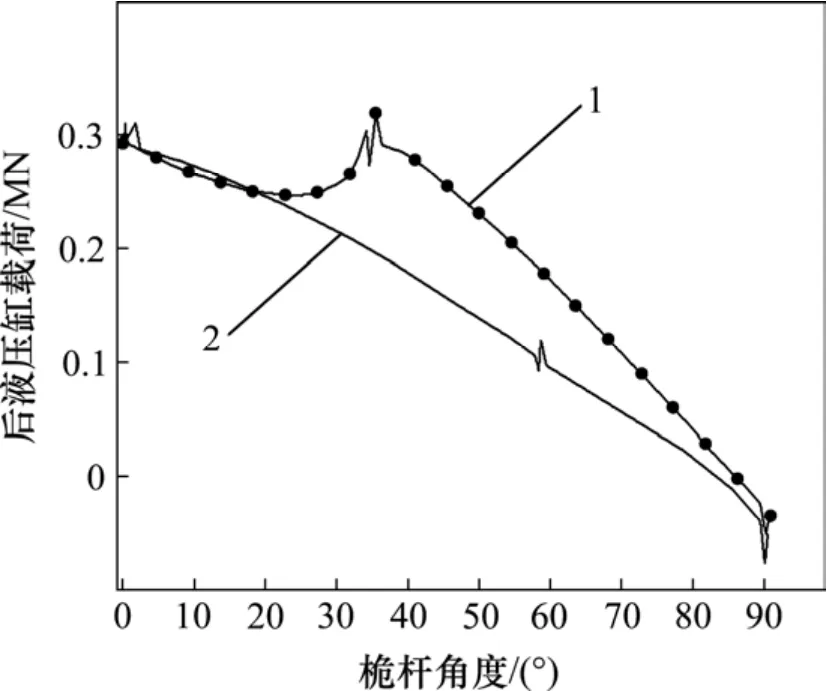
图5 后液压缸载荷Fig.5 Back hydraulic cylinder load
由图4可知:在2 种变幅方式下,变幅启动后,前液压缸载荷均随桅杆角度增大而平缓减小;在桅杆角度0°~58°阶段,变幅方式1 下前液压缸载荷大于变幅方式2;在桅杆角度58°以后,2 种变幅方式下前液压缸载荷比较接近,这是因为桅杆姿态已比较接近。由于桅杆和杆件r1所组成整体的重心变化,在桅杆角度为89°时,前液压缸载荷由正变负,受拉变成受压。
由图5可知:在变幅方式1 下,当桅杆角度为0°~35°时,随桅杆角度增大,后液压缸载荷先减小后增大,这是因为后液压缸拉升力臂变化快,而桅杆、前液压缸、杆件r1、杆件r2、变幅架所组成整体的重心的力臂变化缓慢;当桅杆角度为35°时,后液压缸载荷出现突变冲击,载荷冲击已经大于初始载荷,液压系统产生较大波动甚至超过液压缸的额定压力,这种情况在工程应用中应当避免;当桅杆角度为22°~85°时,在变幅方式2 下,后液压缸载荷明显小于变幅方式1 后液压缸载荷;由于桅杆、杆件r1、杆件r2、前液压缸、变幅架所组成整体的重心变化,当桅杆角度为85°时,后液压缸载荷由正变负,受拉变成受压。根据分析可知,采用变幅方式2,前液压缸和后液压缸的受力情况更好。
4 试验结果与仿真结果比较
在山河智能SWCH588-100M 型全液压履带式桩架上搭建多级组合型大角度变幅机构试验平台,桅杆高度为33 m,发动机额定功率为194 kW,变幅机构液压系统最大流量为90 L/min,最高工作压力为30 MPa。将压力传感器安装在前液压缸、后液压缸与平衡阀之间采集液压缸油压力,将倾角传感器安装在桅杆上采集桅杆角度。设置传感器的采样周期均为0.1 s,桅杆初始角度约等于0°,变幅架初始角度约等于67°。驱动两级变幅的前液压缸和后液压缸由2 个独立的液压先导手柄控制,分别按照变幅方式1和变幅方式2操作先导手柄进行变幅。通过上位机采集记录变幅过程中前液压缸、后液压缸的主动油压力和桅杆角度α,根据油压力和液压缸缸径可计算得到液压缸载荷f1和f2。在2 种变幅方式下,前液压缸和后液压缸载荷试验结果与仿真结果对比如图6所示。
从图6可知:在变幅开始和结束时,试验结果与仿真结果基本相同,在变幅过程中,两者的变化趋势也基本相同,只是由于机器在运转过程中,受液压系统和实际操作的影响,试验数据会有一定震荡;对变幅方式2,在相同桅杆角度下,试验测得的前液压缸和后液压缸载荷与仿真结果最大偏差率分别为12.5%和10.8%。试验结果略大于仿真结果的主要原因是试验平台中前液压缸和后液压缸组实际存在一定对称面夹角。通过对比可以证明本文建立的动力学模型和仿真分析结果的正确性,该动力学模型能够预测该变幅机构的动力学特性。
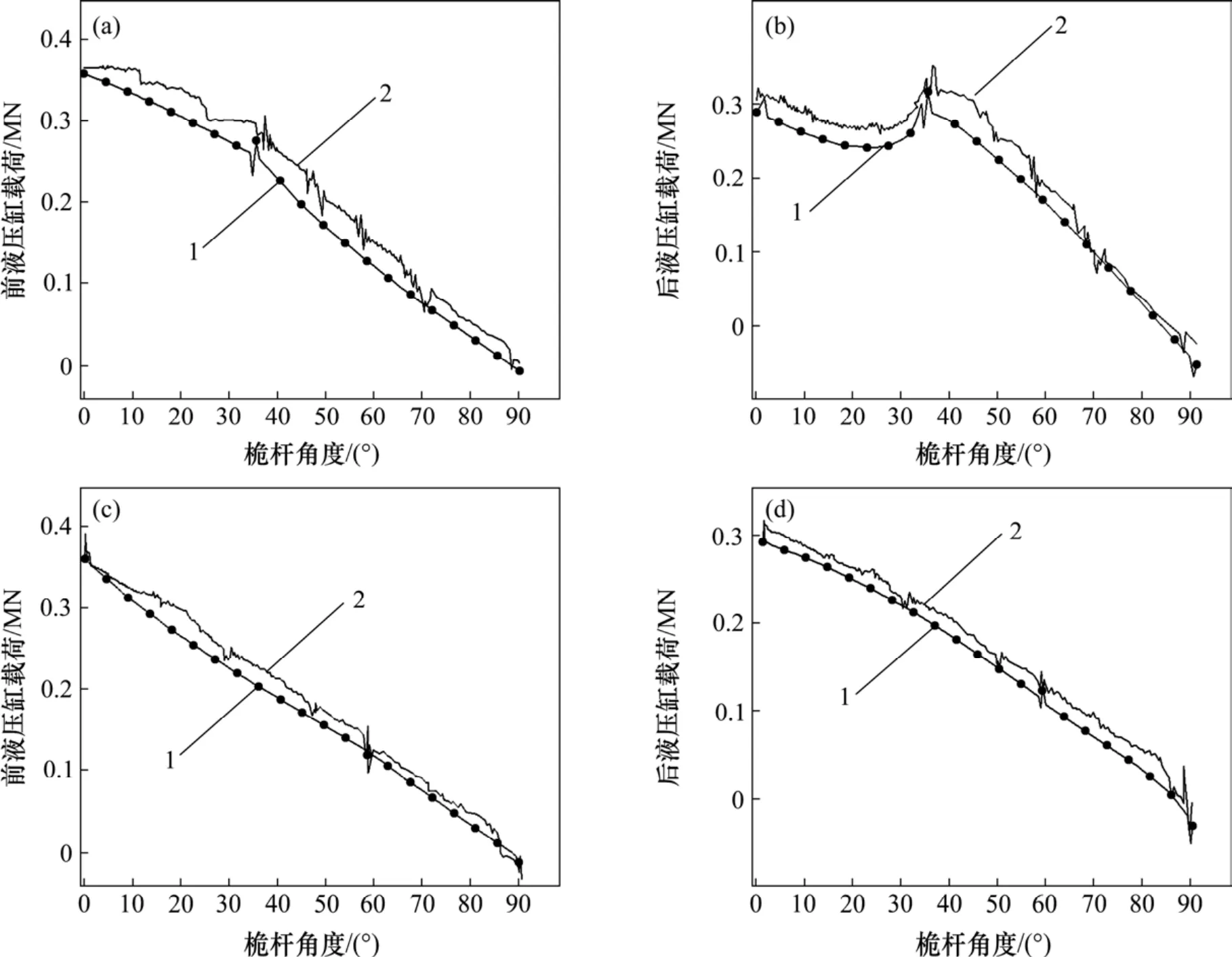
图6 2 种变幅方式下前液压缸和后液压缸载荷试验结果与仿真结果对比Fig.6 Comparison of test loads and simulation results of front hydraulic cylinder and back hydraulic cylinder using two kinds of luffing methods
5 结论
1)前液压缸和后液压缸的初始、末端静载荷只与桅杆的姿态相关,与变幅方式无关。
2)在变幅方式2 中,在初始位置时,前、后液压缸载荷最大。在变幅方式1 中,当桅杆角度到35°左右时,后液压缸出现载荷突变,其值大于初始载荷。
3)当桅杆角度处于22°~85°时,变幅方式2的后液压缸载荷明显比变幅方式1的小;在0°~58°时,变幅方式2的前液压缸载荷明显比变幅方式1的小。
4)与后液压缸先收缩再后液压缸收缩的变幅方式1 相比,前液压缸先收缩再后液压缸收缩的变幅方式2 具有更优的力学性能,桩架的变幅过程更平稳、更安全。
5)所建立的动力学模型不仅可以用于做变幅过程的动力学研究,同时也为后续变幅机构的优化和自动控制奠定了基础。
